Стратегии за победа в някои комбинаторни математически игри

Предлагаме ви няколко комбинаторни математически игри, заедно със стратегиите им за успех, част от курсов проект на математика Филип Петров, доктор по методика на обучението по математика. 

Зад. 1 а): Имаме купчинка от 11 камъчета. Първият играч взема от тях по свое желание 1, 2 или 3 камъчета, след това вторият взема отново 1, 2 или 3, и т.н. до изчерпване на камъчетата. Губи онзи играч, който вземе последното камъче. Намерете стратегия за победа на първия играч.

Решение: Очевидно, ако в последния кръг имаме едно камъче и е на ред вторият играч, то първият задължително печели. Затова първият играч ще се стреми да доведе играта до това положение. Ако той остави на втория играч 5 предмета в предпоследния кръг, очевидно той ще успее да сведе играта до печелившата позиция. Аналогично се връщаме един кръг назад и установяваме, че 9 камъчета са печеливша позиция за първия играч – каквото и да вземе вторият, то първият ще доведе играта до 5 камъчета. Тъй като в началото на играта имаме общо 11 камъчета и първият играч е на ход, ако той вземе 2 камъчета в началото, той ще сведе играта директно в печеливша позиция и оттам ще си осигури победата.

Зад. 1 б): Нека имаме същото условие като задача 1 a), но броят на камъчетата е 30. Намерете печеливша стратегия.

Решение: От решението на миналата задача видяхме, че печелившите позиции се подреждат в редица – 1, 5, 9. Виждаме, че всяка нова печеливша позиция е по-голяма от предходната с 4 => лесно съставяме печелившата редица за 30 камъчета. Тя е 1, 5, 9, 13, 17, 21, 25, 29. Тоест първият играч ще спечели, ако с първия си ход вземе едно камъче и нататък допълва ходовете на втория до числото 4.

Зад.1 в): Нека сега камъчетата са 100, а играчите могат да вземат от едно до 10 камъчета на ход. Има ли печеливша стратегия първият играч?

Решение: Отново трябва да докараме играта до положение да има само едно камъче. Отново ще съставим редицата, но този път тя ще е със стъпка 11: 1, 12, 23, 34, 45, 56, 67, 78, 89, 100. Виждаме, че от самото начало играта е в „печеливша позиция”, но проблемът е, че ние (първият играч) сме на ход. Това означава, че каквото и да играем в първия ход – вторият играч може да сведе играта до печеливша за него позиция и първият играч ще загуби. В тази игра първият играч ще печели само при грешка на втория

Зад.1 обобщение: Нека на масата имаме “n” камъчета, а играчите могат да вземат от 1 до “p” камъчета. Кога имаме стратегия за печалба на първия играч и кога за втория?

Решение: Разсъждавайки аналогично на предходните задачи, съставяме редицата от печеливши позиции: 1, р+2, 2р+3, 3р+4, …, N. Тук нека N e число, по-малко или равно на “n”. Тогава, съобразно посочените правила, играта ще спечели първият играч, ако вземе n-N камъчета. Единствено в ситуацията, когато N=n, първият играч е в губеща позиция (той няма право да вземе 0 камъчета).

Зад.2: Съставете правилото за печеливша стратегия в обратната задача – печели играчът, който вземе последното камъче

Решение: Нека вземем примера от зад.1в – печеливша позиция на първия играч ще бъде, ако останат 11 камъчета, защото каквото и да вземе вторият играч, то първият ще може да вземе остатъка. Отново получаваме редица от печеливши числа: 11, 22, 33, 44, 55, 66, 77, 88, 99, тоест, вземайки едно камъче в началото, ще доведем играта до печеливша позиция.
Нека обобщим – имаме “n” камъчета и играчите могат да вземат по “p” от тях на ход. Печелившата редица ще е: p+1, 2р+2, 3р+3, …, N. Отново N е число, по-малко или равно на “n”. Първият играч има печеливша стратегия във всеки случай, освен ако n=N.

Зад.3: Нека имаме купчина от “n” камъчета. Играчите могат да вземат или 1 или 3 камъчета на ход. За удобство при решението печели този, който вземе последното камъче. Може ли тук да се намери печеливша стратегия?

Решение: Нека за удобство n=11. Лесно можем да се досетим, че играта има изброимо множество от възможни решения. Ние лесно можем да ги представим в дървовидна структура, както е показано на фигурата:

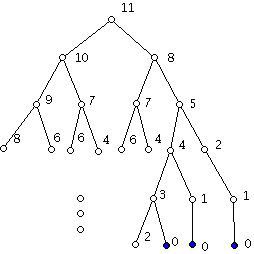
Развивайки дървото, ще забележим, че каквото и да прави първият играч (независимо какви ходове взема), той винаги ще стигне пръв до листото на дървото (тоест до победата).
Проблемът на решението на задачата в такъв вид е, че при по-голямо число “n” дървото става прекалено голямо. Освен това забелязваме, че много от позициите се повтарят – имаме два пъти 7, три пъти 6 и т. н. Затова е по-рационално да разгледаме следния граф:

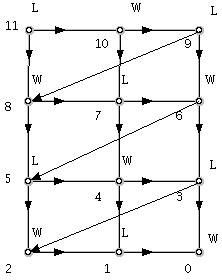
Позициите, означени с “W” (в тях винаги е на ход вторият играч), са печелившите за първия.
Използвайки който и да е от двата графа и разглеждайки повече примери ще стигнем до заключението, че:
a) Ако n e нечетно число, то винаги първият играч печели играта;
б) Ако n е четно число, то винаги вторият играч печели играта.
Така тази игра се обезсмисля при реална игра.

Зад.4: Имаме купчина от 27 камъчета. Всеки от играчите взема от 1 до 4 камъчета. Печели играчът, който завърши с четен брой камъчета. Намерете печеливша стратегия за първия играч

Решение: Както в първите задачи, ще започнем да разсъждаваме от края на задачата.
1) Нека са останали 5 камъчета, което е поне една стъпка преди края на играта. Досега двамата играчи са взели общо 22 камъчета от купчината. За удобство ще кръстим първият играч с А, а вторият с Б. Тази позиция на А е изгодна, ако Б е на ход и има нечетен брой камъчета (в такъв случай очевидно и А ще има нечетен брой камъчета, тъй като сумата трябва да се допълни до 22). Независимо от хода на Б, ние (A) имаме печеливш следващ ход:
– Б взима 1 (Б става четно, остават 4 в купчината) => ние взимаме 3 (ние ставаме четно, остава 1) => Б може да вземе само едно камъче, което го прави нечетен. Нека означим тази комбинация като 1-3-1
– Ако Б вземе 2 (става нечетен) – А взима 3 и става четен: 2-3
– 3-1-1 е печеливша за А
– 4-1 е печеливша за А
Видяхме че при останали 5 камъчета и двамата играчи държащи нечетен брой – то А има печеливша стратегия. Лесно ще се убедим обаче, че в случая, когато Б има четен брой камъчета, то 5 камъчета и Б на ход не е печеливша позиция за А, а напротив – Б има печеливша стратегия.
Така трябва да запомним, че А не трябва да допуска ситуация да остане с четен брой камъчета и пет оставащи в купчината, когато Б е на ход.
2) Изпадайки в подобна ситуация на А няма да остане нищо друго, освен да вземе с едно камъче по-малко и да остави 6 в купчината. Това ще е изгодно за А, ако Б има нечетен брой камъчета (в такъв случай А ще има четен, защото камъчетата трябва да се допълнят до 21 общо взети до тук). Убеждаваме се в това от следните възможни комбинации (припомням, че Б е на ход):
– 1-4-1
– 2-4
– 3-2-1
– 4-2
Убеждаваме се, 6 камъчета в купчината и Б с нечетен брой ще доведе до победа на А. За съжаление обаче има и лош вариант, когато Б е с четен брой камъчета, а има 6 в купчината.
Така запомняме, че А трябва да избегне ситуация, в която да има нечетен брой камъчета и оставащи 6 в купчината, когато Б е на ход.
3) Нека А остави 7 камъчета в купчината и Б е на ход. Ситуацията ще е изгодна за А, ако Б има четен брой камъчета:
– 1-1 свежда играта до 1) и А има печеливша стратегия
– 2-4-1
– 3-4
– 4-2-1
Така при 7 камъчета на масата, А и Б с четен брой камъчета => А има печеливша стратегия. В противен случай трабва да запомним, че А не трябва да допуска тази ситуация
4) Случаите, в които в купа остават 8, 9 или 10 камъчета и Б е на ход винаги са неизгодни за А, тъй като Б лесно ще ги сведе до 1), 2) или 3), но в своя полза.
5) Случаите, в което в купа остават 11, 12 или 13 клечки пък имат печеливша стратегия за А, така че да се сведат до 1), 2) или 3)

Нека сега обобщим стратегията ни за произволна купчина нечетен брой камъчета (ако купчината има четен брой, то имаме равен резултат на финала), чрез следното правило: ако ние сме играч А, то трябва да играем по следния начин
– Ако противникът е с четен брой камъчета в себе си (тук влиза и случая, когато той има нула камъчета, тоест ние сле на първи ход), то ние трябва да му оставим да взима от бройка камъчета с едно по-голяма от кратните числа на 6, тоест трябва да го сведем до 7, 13, 19, 25, … на брой камъчета.
– Ако противникът има нечетен брой камъчета трябва да му оставим камъчета с едно по-малко от кратното число на 6, т.е. 5, 11, 17, 23, …. Ако това не е възможно (тоест ние не можем да достигнем тези числа), то ние го поставяме в позиция на кратно на 6 число, т.е. 6, 12, 18, 24, …

Връщайки се на изходната задача, (купчина от 27 камъчета), виждаме, че първият ни ход ще трябва да е да вземем 2 камъчета. Така А ще има четен брой (2), а Б ще има 0 и ще е на ход. В купчината ще имаме 25 камъчета. Каквото и да вземе Б, ние можем да го сведем до едно от посочените две направления.

Зад. 5 Fruit Game: Това е популярна игра, зададена през 1995-та от 20/20 technologies (2020tech.com). Имаме четири купчини с плодове – лимони, праскови, портокали и банани. Броят на плодовете във всяка от тях е произволен. Можете да вземате произволно количество плодове от една от купчините в ходовете, но не и от две купчини едновременно. Включително имате право да изберете дали да започнете пръв или да дадете шанс на вашия противник да започне играта. Печели този, който вземе последния плод. Намерете печеливша стратегия, така че винаги да спечелите играта.
Примерна игра:

Решение: Нека отново отидем до края на играта и разгледаме няколко случая, в които със сигурност ще спечелим.
– Очевидният е случаят, когато са останали две купчини с по един плод и противникът е на ход (1-1). Така той може да вземе само един плод и на вас не ви остава нищо друго освен да вземете другия. До такава ситуация може да се стигне, ако вие сте на ход и има две купчини – първата с 1, а втората с N плодове, където N>2. Вземаме N-1 плодове от втората купчина и поставяме опонента в 1-1 ситуация;
– „Двойни” позиции са 2-2, 3-3, 4-4 или обобщено N-N, като противникът е на ход. В такъв случай, независимо колко плодове той вземе, ние вземаме същия брой плодове от другата купчина. Това задължително води до позиция 1-1 или директна победа;
– „Два двойника” са 1-1-2-2, 2-2-3-3 или обобщено N-N-M-M (включително N=M). Тактиката ни ще бъде същата – ако противникът вземе p плодове от първата купчина с N, но ние вземаме p плодове от втората купчина N и ги изравнямаме (и отново поставяме противника в N-N-M-M позиция). Така задължително едната група ще се изчерпи, а другата ще бъде сведена до 1-1 ситуация или директна победа;
– 1-2-3, при противникът на ход, отново е печеливша за нас. Каквото и да вземе той, ние свеждаме играта до 1-1 или 2-2;
– Лесно можем да докажем, че 5-4-1, 6-4-2, 6-5-3, 7-4-3, 7-5-2 и 7-6-1 са също печеливши за нас позиции, ако противникът е на ход. Заедно с 1-2-3 това са и единствените печеливши позиции за нас при три купчини и противникът на ход;
– За съжаление, играта започва с четири купчини и вариантите за игра са много. Някои от печелившите позиции са 5-4-3-2, 7-6-5-4, 6-4-3-1, 6-5-2-1, 7-4-2-1, 7-5-3-1, 7-6-3-2, и т.н.

За съжаление виждаме, че вариантите са прекалено разнородни и при положение, че имаме по повече от 7 плодове в купчина в началото на играта, ние много трудно бихме могли да запомним печелившите позиции. Затова методът на изчерпването ще трябва да отпадне и да търсим зависимост между тези печеливши позиции.
Тази игра всъщност е вариант на играта Nim (където и купчините са произволен брой). Тя е напълно изследвана от C. L. Bouton (математик от Harvard University) през 1902. Решението е намерено, като се изследват числата в бинарен вид и на четността и нечетността на сбора им. Той е изследвал сумата на числата (представени в бинарен вид) в купчините, като е сумирал без пренасяне, т. е. 0+0=0, 0+1=1 и 1+1=0. Дори този вид събиране, дори в последствие, е наречен nim-събиране. Самият сбор е наречен индикатор. Bouton е доказал следните две теореми:

Теорема 1: Ако индикаторът на сбора е нула (0), то какъвто и брой елементи да вземем от която и да е купчина, няма да можем да достигнем до нова конфигурация с индикатор нула.

Теорема 2: Ако индикаторът на сбора съдържа поне една единица (1), винаги можем да премахнем точно определен брой елементи от една от купчините, така че новият индикатор да е нула (0).
Алгоритъмът от доказателството е, че вземаме най-лявата единица от сбора, намираме единица от колоната, в която се намира тя и премахваме редът й. Останалите редове сумираме и вземаме индикатора им => превръщаме индикатора в десетично число. Нека това число е “N” и в премахнатия ред (купчина) има “n” на брой елементи => ако премахнем n-N елемента от тази купчина, ще получим схема с индикатор нула

Връщайки се в нашата задача и гледайки досега изведените печеливши позиции, ще забележим, че всички те са с индикатор нула, тоест ако противникът играе, nim-сборът на бинарните числа трябва да е с индикатор 0. Ето и няколко примера:

-	6-5-2-1:
6:	110
5:	101
2:	010
1:	001
	----
	000

-	7-6-3-2:
7:	111
6:	110
3:	011
2:	010
	----
	000

-	10-10-1500-1500 (N-N-M-M)
1351:	10101000111
1351:	10101000111
1500:	10111011100
1500:	10111011100
	-----------------
	00000000000

Тоест ние можем да спечелим Fruit Game при всички комбинации:
– Ако началното условие на играта не е с индикатор 0 ние играем първи. Веднага вземаме нужния брой елементи от една от купчините и поставяме противника в ситуация с индикатор нула, което е печеливша позиция;
– Ако пък началното условие на играта е с индикатор 0 – то ние се отказваме от първия ход и даваме на нашия противник да играе. Тъй като по теорема 1 не е възможно той да ни сведе до друга ситуация с индикатор нула – то ние сме по условие в печеливша позиция.

Играта може да се развие естествено и с “n” на брой купчини, като алгоритъмът за победа е същият.

Ако искате да поиграете отидете на следния адрес:
http://king.2020tech.com/cgi-bin/nim/nim

Зад.6: Имаме лента от хартия, разделена на осем квадратчета, кръстени съответно a,b,c,d,e,f, g и h. В квадратчетата d, f и h са сложени камъчета. Играчите могат да преместват произволно камъче в кое да е квадратче наляво (може да прескача и дори да застъпва друго камъче). Губи играчът, който остане без възможен ход. Покажете, че първият играч има печеливша стратегия.

Решение: Това очевидно е аналог на игра Nim с три купчини със стартова позиция 4-6-8
Тъй като индикаторът на Nim-сборът е различен от 0 => първият играч има печеливша стратегия.

Зад.7 Nim с връщане: Нека разгледаме игра на Nim с “n” купчини с произволно количество камъчета във всяка. Условието на играта е същото като на Nim, но вече играчите ще могат да запазват камъчетата, които са взели в отделна своя купчина. Всеки от тях има право при всеки свой ход да поставя колкото си иска камъчета от своята лична купчина обратно в някоя купчина от играта (но не може едновременно да взима и слага камъчета в един ход). Играчите, дори в самото начало на играта, имат по “p” камъка в своята купчина (p е по-голямо или равно на нула). Каква е печелившата стратегия за първия играч, ако играта започва с индикатор, различен от нула?

Решение: Както и преди, играта ще се върти около позициите с индикатор нула. Първият участник задължително още с първия си ход ще я приведе до печеливша за самия него позиция. Въпросът е възможно ли е вторият играч да добави камъчета в една от купчините, така че да изведе играта от една позиция с индикатор нула в друга? Оказва се, че, както при премахване, така и при добавяне на камъни, това не е възможно. Така се получава, че ако вторият играч добавя камъчета, на следващия си ход ще ги взима и ще докарва играта обратно в печеливша позиция. Тъй като камъчетата в личната купчина на втория играч са ограничено количество, в един момент ще свършат и играта ще продължи като обикновен Nim (тоест не достигаме до безкрайна игра).

Зад. 8: Цзян ши дзи: Това е китайска национална игра, разширяваща Nim с допълнително условие. Имаме две купчини с камъни. Всеки играч може да вземе произволен брой камъни от една от купчините или да вземе произволен брой камъни и от двете купчини едновременно (но задължително равен брой и от двете). Печели играчът взел последният камък. Намерете стратегия за победа на първия играч

Решение: Отново ще се поставим на мястото на първия играч и ще започнем от базови ситуации, в които ние поставяме опонента в печеливша за нас позиция. Очевидна такава позиция е 1-2, тъй като каквото и да вземе опонентът – ние можем да вземем остатъка. Така разбираме, че ако ние сме на ход и имаме ситуация 1-N (N>2) – то ние задължително взимаме N-2 елемента от втората купчина и оставяме играта в печелившата за нас 1-2 позиция.
Ако сме на ход при ситуация 2-N, случаят се свежда до предишния – ние можем да премахнем N-1 камъка от втората купчина и да оставим играта в 2-1, което е същото като 1-2
Да разгледаме ситуация 3-N, в която ние сме на ход:
– Ако вземем N-1 камъка, играта ще стане 3-1, след което вторият играч ще я сведе до 2-1 в негова полза => 3-1 не е печелившо за нас
– Ако вземем N-2 камъка, играта ще стане 3-2. Вторият играч ще вземе по един камък от всяка купчина и играта ще е отново 2-1 в негова полза
– Ако вземем N-3 камъка, то вторият играч попада в 3-3 и автоматично печели
– Ако вземем N-4 камъка, играта става 3-4. Вторият играч ще вземе 2+2 камъка от двете купчини и ние ще попаднем в ситуация 2-1 в негова полза
– Ако вземем N-5 камъка, ще попаднем в ситуация 3-5. Оказва, се че това е печеливша за нас позиция. Колкото и камъка да вземе вторият играч от първата или втората купчина – ние лесно свеждаме играта до 1-2 за нас. Аналогична е ситуацията, когато той взима равен брой камъни от двете купчини

Чрез аналогични изчисления виждаме, че ситуацията 4-N, когато ние сме на ход, ще ни изведе до печелившата комбинация 4-7
Ситуацията 5-N не е интересна, тъй като я свеждаме до познатата 5-3, която е аналогична на 3-5
При 6-N намираме печеливша комбинация 6-10
7-N не е интересна, защото свеждаме играта до 7-4, аналогична на 4-7
При 8-N свеждаме до печелившата комбинация 8-13
При 9-N свеждаме до печелившата комбинация 9-15
Ситуацията 10-N не е интересна, защото свеждаме до 10-6, т.е. 6-10
… и т.н.

Да наредим съществените печеливши комбинации в редица:
1-2, 3-5, 4-7, 6-10, 8-13, 9-15, … (*)
Нека означим елементите на първата купчина с a_i, а на втората с b_i. Извеждаме следната зависимост за втората купчина:
b_n = a_n + n
Числата a_i в редицата пък се образуват, като винаги вземаме най-малкото възможно число, което не сме срещали измежду предишните a_k и b_k

Така ние (първият играч) можем да спечелим винаги, когато играта започва от комбинация, различна от изброените в (*)

П.С. можем да забележим също, че печелившите комбинации са цялата част от числата на златното сечение:
a_n = [(1+sqrt(5))*n/2] и b_n = [(3+sqrt(5))*n/2]

по "Математически забавления" на Мартин Гарднър