

–î–∞ —Å–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–∏–º –Ω–∏–µ, –∂–∏—Ç–µ–ª–∏—Ç–µ –Ω–∞ —Ç—Ä–∏–º–µ—Ä–Ω–∏—è —Å–≤—è—Ç –æ–±–µ–∫—Ç–∏ –æ—Ç —á–µ—Ç–∏—Ä–∏–º–µ—Ä–Ω–æ—Ç–æ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ –∏–∑–≥–ª–µ–∂–¥–∞ –ø–æ—á—Ç–∏ –Ω–µ–ø–æ—Å–∏–ª–Ω–∞ –∑–∞–¥–∞—á–∞, –Ω–æ –≤ —Ç–µ–º–∞—Ç–∞ "–ü–ª–∞—Ç–æ–Ω–æ–≤–∏—Ç–µ —Ç–µ–ª–∞ –∏ —Ç–µ—Ö–Ω–∏—Ç–µ –±—Ä–∞—Ç–æ–≤—á–µ–¥–∏ –æ—Ç –≤–∏—Å—à–∏—Ç–µ –∏–∑–º–µ—Ä–µ–Ω–∏—è" –≤–µ—á–µ –≤–∏ –∑–∞–ø–æ–∑–Ω–∞—Ö–º–µ —Å –µ–¥–∏–Ω –æ—Ç –Ω–∞—á–∏–Ω–∏—Ç–µ - –º–µ—Ç–æ–¥–∞ –Ω–∞ –∞–Ω–∞–ª–æ–≥–∏—è—Ç–∞. –¢—É–∫ —â–µ –ø—Ä–æ–¥—ä–ª–∂–∏–º –∏ —Å –¥—Ä—É–≥–∏.
–°–µ—á–µ–Ω–∏—è
–ú–æ–∂–µ¬Ý–¥–∞ –æ–±—è—Å–Ω–∏–º –Ω–∞ –¥–≤—É–º–µ—Ä–Ω–∏—Ç–µ –ø–ª–æ—Å–∫–∏ –≥—É—â–µ—Ä–∏ –Ω–∞ –ï—à–µ—Ä –∏–ª–∏ –Ω–∞ —Ñ–ª–∞—Ç–ª–µ–Ω–¥–µ—Ä–∏—Ç–µ –∫–∞–∫–≤–æ –µ —Ç–µ—Ç—Ä–∞–µ–¥—ä—Ä –∫–∞—Ç–æ –≥–æ –Ω–∞—Ä–µ–∂–µ–º –Ω–∞ "—Ñ–∏–ª–∏–π–∫–∏". –¢–æ–∑–∏ –º–µ—Ç–æ–¥ —Å–µ –∏–∑–ø–æ–ª–∑–≤–∞ –≤ —Ç–æ–º–æ–≥—Ä–∞—Ñ–∏—è—Ç–∞: —Ä–∞–∑–≥–ª–µ–∂–¥–∞—Ç —Å–µ –ø–æ—Ä–µ–¥–∏—Ü–∞ –æ—Ç —Å–Ω–∏–º–∫–∏ –Ω–∞ —á–æ–≤–µ—à–∫–æ—Ç–æ —Ç—è–ª–æ –≤ –Ω–∞–ø—Ä–µ—á–Ω–æ —Å–µ—á–µ–Ω–∏–µ, –∞ —Å–ª–µ–¥ —Ç–æ–≤–∞ —Å–µ –ø–æ–ª—É—á–∞–≤–∞ —Ç—Ä–∏–∏–∑–º–µ—Ä–Ω–∞ –∫–∞—Ä—Ç–∏–Ω–∞.
–ü–æ–≥–ª–µ–¥–Ω–µ—Ç–µ –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª–Ω–æ—Å—Ç—Ç–∞ –Ω–∞ —Ç–µ–∑–∏ –Ω–∞–ø—Ä–µ—á–Ω–∏ —Å–µ—á–µ–Ω–∏—è:

–ù–∞–¥—è–≤–∞–º —Å–µ, —á–µ –ª–µ—Å–Ω–æ —â–µ —Ä–∞–∑–ø–æ–∑–Ω–∞–µ—Ç–µ –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª–Ω–∏—Ç–µ —Å–µ—á–µ–Ω–∏—è –Ω–∞ –∫—É–±. –î–∞, –Ω–æ –∑–∞—â–æ—Ç–æ –∏–º–∞–º–µ –æ–ø–∏—Ç–∞ –Ω–∞ 3D —Å—ä—â–µ—Å—Ç–≤–∞.
–ö–æ–≥–∞—Ç–æ –º–Ω–æ–≥–æ—Å—Ç–µ–Ω—ä—Ç —Å–µ –ø—Ä–µ–º–µ—Å—Ç–≤–∞ –≤ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ—Ç–æ –∏ —Å–µ –ø—Ä–µ—Å–∏—á–∞ —Å —Ä–∞–≤–Ω–∏–Ω–∞—Ç–∞ –Ω–∞¬Ý—Ñ–ª–∞—Ç–ª–µ–Ω–¥–µ—Ä–∏—Ç–µ, —Å–µ—á–µ–Ω–∏–µ—Ç–æ –º—É –µ –º–Ω–æ–≥–æ—ä–≥—ä–ª–Ω–∏–∫. –ü—Ä–∏ –¥–≤–∏–∂–µ–Ω–∏–µ—Ç–æ –Ω–∞ –º–Ω–æ–≥–æ—Å—Ç–µ–Ω–∞, –º–Ω–æ–≥–æ—ä–≥—ä–ª–Ω–∏–∫—ä—Ç —Å–µ –ø—Ä–æ–º–µ–Ω—è –∏ –≤ –∫—Ä–∞–π–Ω–∞ —Å–º–µ—Ç–∫–∞, –∏–∑—á–µ–∑–≤–∞ –≤ –º–æ–º–µ–Ω—Ç–∞, –∫–æ–≥–∞—Ç–æ —Ç—è–ª–æ—Ç–æ –æ–∫–æ–Ω—á–∞—Ç–µ–ª–Ω–æ –ø—Ä–µ–º–∏–Ω–µ –ø—Ä–µ–∑ —Ä–∞–≤–Ω–∏–Ω–∞—Ç–∞.¬Ý–§–ª–∞—Ç–ª–µ–Ω–¥–µ—Ä–∏—Ç–µ –≤–∏–∂–¥–∞—Ç —Å–∞–º–æ –º–Ω–æ–≥–æ—ä–≥—ä–ª–Ω–∏—Ü–∏, –Ω–æ –≥–∏ –≤–∏–∂–¥–∞—Ç –≤ –¥–≤–∏–∂–µ–Ω–∏–µ, –º–æ–≥–∞—Ç –¥–∞ –Ω–∞–±–ª—é–¥–∞–≤–∞—Ç –ø—Ä–æ–º–µ–Ω—è—â–∏—Ç–µ –∏–º —Å–µ —Ñ–æ—Ä–º–∏. –°–ª–µ–¥ –∫–∞—Ç–æ –ø–æ–Ω–∞—Ç—Ä—É–ø–∞—Ç –º–∞–ª–∫–æ –æ–ø–∏—Ç, –≤—ä–∑–º–æ–∂–Ω–æ –µ –≤ –∫—Ä–∞–π–Ω–∞ —Å–º–µ—Ç–∫–∞ –¥–∞ –ø–æ–ª—É—á–∞—Ç –µ–¥–Ω–∞ –∏–Ω—Ç—É–∏—Ç–∏–≤–Ω–∞ –ø—Ä–µ–¥—Å—Ç–∞–≤–∞ –∑–∞ —Ç–æ–≤–∞ –∫–∞–∫–≤–æ –µ –º–Ω–æ–≥–æ—Å—Ç–µ–Ω, –≤—ä–ø—Ä–µ–∫–∏ —á–µ –Ω–µ —Å–∞ –≤ —Å—ä—Å—Ç–æ—è–Ω–∏–µ –¥–∞ –≥–æ –≤–∏–¥—è—Ç –≤ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ—Ç–æ.
–î–∞ —Å–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–∏–º, —á–µ —Å–º–µ 2D —Å—ä—â–µ—Å—Ç–≤–∞, –∫–æ–∏—Ç–æ —Å–∏ –Ω—è–º–∞—Ç –Ω–∏–∫–∞–∫–≤–∞ –ø—Ä–µ–¥—Å—Ç–∞–≤–∞ –∫–∞–∫–≤–æ –µ –µ —Ü–∏–ª–∏–Ω–¥—ä—Ä. –ù–∏–µ –Ω—è–º–∞ –∫–∞–∫ –¥–∏—Ä–µ–∫—Ç–Ω–æ –≤–∏–¥–∏–º —Ç–∞–∫—ä–≤ –æ–±–µ–∫—Ç, –∑–∞—â–æ—Ç–æ –Ω–∞—à–∞—Ç–∞ —Ä–µ—Ç–∏–Ω–∞ –µ —Å–∞–º–æ 1D, –∞ –µ –Ω–µ–æ–±—Ö–æ–¥–∏–º–∞ 2D —Ä–µ—Ç–∏–Ω–∞, –∫–æ—è—Ç–æ –¥–∞ –º–æ–∂–µ –∞–¥–µ–∫–≤–∞—Ç–Ω–æ –¥–∞ –≤—ä–∑–ø—Ä–∏–µ–º–µ 3D –æ–±–µ–∫—Ç. –î–∞ —Å–µ –ø—Ä–æ—É—á–∏–º –∫–∞–∫–≤–æ —Å–µ —Å–ª—É—á–≤–∞, –∫–æ–≥–∞—Ç–æ –µ–¥–∏–Ω —Ü–∏–ª–∏–Ω–¥—ä—Ä –º–∏–Ω–∞–≤–∞ –ø—Ä–µ–∑ –Ω–∞—à–∏—è 2D —Å–≤—è—Ç:
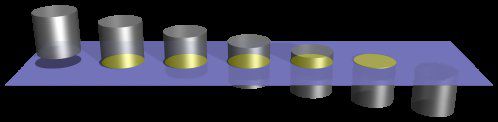
–ê–∫–æ —Ü–∏–ª–∏–Ω–¥—ä—Ä—ä—Ç —Å–µ —Å–ø—É—Å–∫–∞ –ø—Ä–µ–∑ –Ω–∞—à–∏—è —Å–≤—è—Ç –≤–µ—Ä—Ç–∏–∫–∞–ª–Ω–æ, —â–µ –≤–∏–¥–∏–º –ø–æ—Ä–µ–¥–∏—Ü–∞ –æ—Ç –∫—Ä—ä–≥–ª–∏ –Ω–∞–ø—Ä–µ—á–Ω–∏ —Å–µ—á–µ–Ω–∏—è, –≤—Å–∏—á–∫–∏ —Å –µ–¥–Ω–∞–∫—ä–≤ —Ä–∞–∑–º–µ—Ä.

2D —Å—ä—â–µ—Å—Ç–≤–∞ –Ω–µ –º–æ–≥–∞—Ç –¥–∞ –≤–∏–¥—è—Ç –≤—Å—ä—â–Ω–æ—Å—Ç –≥–æ—Ä–Ω–æ—Ç–æ –∏–∑–æ–±—Ä–∞–∂–µ–Ω–∏–µ –¥–∏—Ä–µ–∫—Ç–Ω–æ; —Ç–µ –º–æ–≥–∞—Ç –¥–∞ –≤–∏–¥—è—Ç –∫—Ä—ä–≥–ª–æ—Ç–æ —Å–µ—á–µ–Ω–∏–µ —Å–∞–º–æ –æ—Ç—Å—Ç—Ä–∞–Ω–∏. –ù–∞–ø—Ä–µ—á–Ω–∏—Ç–µ —Å–µ—á–µ–Ω–∏—è —â–µ –∏–∑–≥–ª–µ–∂–¥–∞—Ç –∫–∞—Ç–æ –æ—Ç—Å–µ—á–∫–∏, –∫–æ–∏—Ç–æ —â–µ –ø–æ–∫–∞–∑–≤–∞—Ç –∫—Ä–∏–≤–∏–Ω–∞—Ç–∞, –∞–∫–æ –∏–º–∞ –æ–∫–æ–ª–Ω–∏ —Å–≤–µ—Ç–ª–∏–Ω–Ω–∏ –∏–∑—Ç–æ—á–Ω–∏—Ü–∏. (–ö–∞–∫—Ç–æ –Ω–∏–µ, 3D- —Ö–æ—Ä–∞—Ç–∞ –º–æ–∂–µ–º –¥–∞ —Ä–∞–∑–±–µ—Ä–µ–º, —á–µ –Ω–∞ –ø–æ-–≥–æ—Ä–Ω–∞—Ç–∞ –∫–∞—Ä—Ç–∏–Ω–∫–∞ –µ —Ü–∏–ª–∏–Ω–¥—ä—Ä –±–ª–∞–≥–æ–¥–∞—Ä–µ–Ω–∏–µ –Ω–∞ —Å–≤–µ—Ç–ª–æ—Å–µ–Ω–∫–∏—Ç–µ).¬Ý
–¢–∞–∫–∞ –∏–ª–∏ –∏–Ω–∞—á–µ, –µ–¥–Ω–æ 2D —Å—ä—â–µ—Å—Ç–≤–æ –º–æ–∂–µ –¥–∞ –∑–∞–∫–ª—é—á–∏, —á–µ —Ü–∏–ª–∏–Ω–¥—ä—Ä—ä—Ç —Ç—Ä—è–±–≤–∞ –¥–∞ –µ –Ω–µ—â–æ –∫—Ä—ä–≥–ª–æ.
–î–∞ —Å–ø—É—Å–Ω–µ–º —Ü–∏–ª–∏–Ω–¥—ä—Ä–∞ —Å –µ–¥–Ω–∞ —Ä–∞–∑–ª–∏—á–Ω–∞ –æ—Ä–∏–µ–Ω—Ç–∞—Ü–∏—è:
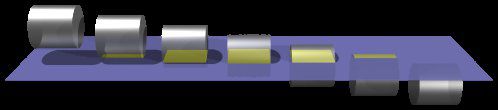
–¢–æ–∑–∏ –ø—ä—ǬÝ2D —Å—ä—â–µ—Å—Ç–≤–∞—Ç–∞ –Ω—è–º–∞ –¥–∞ –≤–∏–¥—è—Ç –Ω–∏—â–æ –∫—Ä—ä–≥–ª–æ, –∞ —Å–∞–º–æ –ø–æ—Ä–µ–¥–∏—Ü–∞ –æ—Ç –ø—Ä–∞–≤–æ—ä–≥—ä–ª–Ω–∏ –Ω–∞–ø—Ä–µ—á–Ω–∏ —Å–µ—á–µ–Ω–∏—è, –∫–æ–∏—Ç–æ –∏–∑–≥–ª–µ–∂–¥–∞, —á–µ —Ä–∞—Å—Ç–∞—Ç –∏ —Å–µ —Å–≤–∏–≤–∞—Ç –∫–∞—Ç–æ –¥—ä–ª–∂–∏–Ω–∞—Ç–∞ –∏–º –æ—Å—Ç–∞–≤–∞ –ø–æ—Å—Ç–æ—è–Ω–Ω–∞. –û—Ç —Ç–æ–≤–∞¬Ý—Ç–µ –º–æ–≥–∞—Ç –¥–∞ –∑–∞–∫–ª—é—á–∞—Ç, —á–µ —Ü–∏–ª–∏–Ω–¥—ä—Ä—ä—Ç —Ç—Ä—è–±–≤–∞ –¥–∞ –∏–º–∞ –Ω–µ—â–æ –ø—Ä–∞–≤–æ—ä–≥—ä–ª–Ω–æ.

–û—Ç —Ç–µ–∑–∏ –¥–≤–µ –ø–æ—Ä–µ–¥–∏—Ü–∏ —Å–µ—á–µ–Ω–∏—è –º–æ–∂–µ –¥–∞ —Å–µ –∏–∑–≤–ª–µ—á–µ —Ü–µ–Ω–Ω–∞—Ç–∞ –∏ –≤—è—Ä–Ω–∞ –∏–Ω—Ñ–æ—Ä–º–∞—Ü–∏—è, —á–µ –µ–¥–∏–Ω 3D —Ü–∏–ª–∏–Ω–¥—ä—Ä –µ –Ω–µ—â–æ, –∫–æ–µ—Ç–æ –µ –µ–¥–Ω–æ–≤—Ä–µ–º–µ–Ω–Ω–æ –∫—Ä—ä–≥–ª–æ –∏ –ø—Ä–∞–≤–æ—ä–≥—ä–ª–Ω–æ.¬Ý
–î–∞, –Ω–æ –∞–∫–æ —Å–º–µ¬Ý2D —Å—ä—â–µ—Å—Ç–≤–∞, —Ç—Ä—É–¥–Ω–æ —â–µ –º–æ–∂–µ–º –¥–∞ –ø—Ä–æ—É–º–µ–µ–º –∫–∞–∫ –µ–¥–Ω–æ –Ω–µ—â–æ –º–æ–∂–µ –¥–∞ –±—ä–¥–µ –∏ –∫—Ä—ä–≥–ª–æ, –∏ –ø—Ä–∞–≤–æ—ä–≥—ä–ª–Ω–æ –µ–¥–Ω–æ–≤—Ä–µ–º–µ–Ω–Ω–æ. –ö–∞—Ç–æ 2D —Å—ä—â–µ—Å—Ç–≤–∞, –Ω–∏–µ –∏–º–∞–º–µ –æ–ø–∏—Ç —Å–∞–º–æ —Å 2D —Ñ–æ—Ä–º–∏ –∏ –Ω–∏–∫–æ—è –æ—Ç —Ç—è—Ö –Ω–µ —Å–∞ –µ–¥–Ω–æ–≤—Ä–µ–º–µ–Ω–Ω–æ –∫—Ä—ä–≥ –∏ –ø—Ä–∞–≤–æ—ä–≥—ä–ª–Ω–∏–∫.
–î–∞–ª–∏ –∞–∫–æ —Ü–∏–ª–∏–Ω–¥—ä—Ä—ä—Ç –º–∏–Ω–µ —á—Ä–µ–∑ –Ω–∞—à–∏—è 2D —Å–≤—è—Ç –ø–æ–¥ —ä–≥—ä–ª –æ—Ç 45 –≥—Ä–∞–¥—É—Å–∞ —â–µ –ø–æ–ª—É—á–∏–º –ø–æ–≤–µ—á–µ –ø—Ä–µ–¥—Å—Ç–∞–≤–∞?

–ü–æ–ª—É—á–µ–Ω–∏—Ç–µ –Ω–∞–ø—Ä–µ—á–Ω–∏ —Å–µ—á–µ–Ω–∏—è —Å–∞ –æ—â–µ –ø–æ-–æ–∑–∞–¥–∞—á–∞–≤–∞—â–∏ - –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª–Ω–æ—Å—Ç –æ—Ç –æ—Ç—Å–µ—á–µ–Ω–∏ –µ–ª–∏–ø—Å–∏:

–û—Å–≤–µ–Ω –∞–∫–æ –ø—Ä–µ–¥–≤–∞—Ä–∏—Ç–µ–ª–Ω–æ –Ω–µ –∑–Ω–∞–µ–º, –≤–µ—Ä–æ—è—Ç–Ω–æ –Ω—è–º–∞ –¥–∞ –º–æ–∂–µ–º –¥–∞ –∏–∑–≤–ª–µ—á–µ–º —Ñ–æ—Ä–º–∞—Ç–∞ –Ω–∞ —Ü–∏–ª–∏–Ω–¥—ä—Ä –æ—Ç —Ç–µ–∑–∏ —Å–µ—á–µ–Ω–∏—è.¬Ý
–¢–æ–≤–∞ –∏–ª—é—Å—Ç—Ä–∏—Ä–∞ –æ—Å–Ω–æ–≤–Ω–∞ —Å–ª–∞–±–æ—Å—Ç –Ω–∞ –º–µ—Ç–æ–¥–∞ –Ω–∞ –Ω–∞–ø—Ä–µ—á–Ω–∏—Ç–µ —Å–µ—á–µ–Ω–∏—è - –º–∞–∫–∞—Ä –∏ –¥–∞ –¥–∞–≤–∞—Ç –ø–æ–ª–µ–∑–Ω–∞ –∏–Ω—Ñ–æ—Ä–º–∞—Ü–∏—è, —Ç—è —Ç—Ä—É–¥–Ω–æ —Å–µ —Å–∏–Ω—Ç–µ–∑–∏—Ä–∞ –≤ –µ–¥–∏–Ω —Å—ä–≥–ª–∞—Å—É–≤–∞–Ω –º–æ–¥–µ–ª –Ω–∞ —Ä–µ–∞–ª–Ω–∏—è –æ–±–µ–∫—Ç.¬Ý
–ù—è–º–∞ –¥–∞ –∏–º –µ –ª–µ—Å–Ω–æ –Ω–∞ –ø–ª–æ—Å–∫–∏—Ç–µ¬Ý—Ñ–ª–∞—Ç–ª–µ–Ω–¥–µ—Ä–∏ –¥–∞ –ø–æ–∑–Ω–∞—è—Ç –∫—É–±–∞, –≤–∏–∂–¥–∞–π–∫–∏ —à–µ—Å—Ç–æ—ä–≥—ä–ª–Ω–æ —Å–µ—á–µ–Ω–∏–µ, –Ω–æ –Ω–∏–µ –∫–∞—Ç–æ 3D —Å—ä—â–µ—Å—Ç–≤–∞, –∏–º–∞–º–µ –∏–∑–≤–µ—Å—Ç–Ω–∏ –ø–æ–∑–Ω–∞–Ω–∏—è –Ω–∞ 3D –≥–µ–æ–º–µ—Ç—Ä–∏—è—Ç–∞, –∑–∞ –¥–∞ —Å–µ –¥–æ—Å–µ—Ç–∏–º, —á–µ —Ç–æ–≤–∞ –µ –∫—É–±.

A–∫–æ –ø—Ä–æ—Å–ª–µ–¥–∏—Ç–µ –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª–Ω–æ—Å—Ç—Ç–∞ –Ω–∞ —Å–µ—á–µ–Ω–∏—è –Ω–∞ —á–µ—Ç–∏—Ä–∏–º–µ—Ä–µ–Ω –æ–±–µ–∫—Ç —Å 3D –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ—Ç–æ, –º–æ–∂–µ –ª–∏ –¥–∞ —Ä–∞–∑–±–µ—Ä–µ–º –∫–∞–∫–≤–æ –µ —Ç—è–ª–æ—Ç–æ?
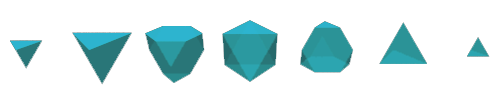
–í–µ—Ä–æ—è—Ç–Ω–æ –Ω–µ, –æ—Å–≤–µ–Ω –∞–∫–æ –Ω–µ –≥–æ –∑–Ω–∞–µ–º –ø—Ä–µ–¥–≤–∞—Ä–∏—Ç–µ–ª–Ω–æ, –±–µ–∑ –∏–Ω—Ç—É–∏—Ç–∏–≤–Ω–æ —Ä–∞–∑–±–∏—Ä–∞–Ω–µ –Ω–∞ 4D, —â–µ –µ –º–Ω–æ–≥–æ —Ç—Ä—É–¥–Ω–æ –¥–∞ –≤—ä–∑—Å—Ç–∞–Ω–æ–≤–∏–º –æ—Ä–∏–≥–∏–Ω–∞–ª–Ω–∏—è –æ–±–µ–∫—Ç –æ—Ç —Ç—è—Ö.
–û—Å–Ω–æ–≤–Ω–∏—è—Ç –ø—Ä–æ–±–ª–µ–º —Å –Ω–∞–ø—Ä–µ—á–Ω–∏ —Å–µ—á–µ–Ω–∏—è –µ, —á–µ –Ω–∏–µ –Ω–µ –º–æ–∂–µ–º –¥–∞ –≤–∏–¥–∏–º –∏–∑—Ü—è–ª–æ –æ–±–µ–∫—Ç–∞, –∞ —Å–∞–º–æ "–Ω–∞ –ø–∞—Ä—á–µ". –í–∞–∂–Ω–∏ —Ö–∞—Ä–∞–∫—Ç–µ—Ä–∏—Å—Ç–∏–∫–∏, –∫–∞—Ç–æ –Ω–∞–ø—Ä–∏–º–µ—Ä –±—Ä–æ—è –∏ —Ñ–æ—Ä–º–∞—Ç–∞ –Ω–∞ —Å—Ç–µ–Ω–∏—Ç–µ, –±—Ä–æ—è—Ç –Ω–∞ –≤—ä—Ä—Ö–æ–≤–µ—Ç–µ (—ä–≥–ª–∏—Ç–µ), –∫–∞–∫—Ç–æ –∏ —Ü—è–ª–æ—Å—Ç–Ω–∞—Ç–∞ —Ñ–æ—Ä–º–∞ –Ω–∞ –æ–±–µ–∫—Ç–∞, –æ—Å—Ç–∞–≤–∞—Ç —Å–∫—Ä–∏—Ç–∏.¬Ý–ù–∏–µ —â–µ —Ç—Ä—è–±–≤–∞ –¥–∞ –∞–Ω–∞–ª–∏–∑–∏—Ä–∞–º–µ —Ç–µ–∑–∏ —Å–µ—á–µ–Ω–∏—è –º–Ω–æ–≥–æ –≤–Ω–∏–º–∞—Ç–µ–ª–Ω–æ, –∑–∞ –¥–∞ –ø–æ–ª—É—á–∏–º —Ç–∞–∑–∏ –∏–Ω—Ñ–æ—Ä–º–∞—Ü–∏—è.¬Ý
–ù–µ–∫–∞ –Ω–µ –∑–∞–±—Ä–∞–≤—è–º–µ, —á–µ "—Ä–µ–∂–µ–º" —Å –±–µ–∑–∫—Ä–∞–µ–Ω –æ–±–µ–∫—Ç —Å —Ä–∞–∑–º–µ—Ä–Ω–æ—Å—Ç N-1 - —Ç.–µ. —Ä–µ–∂–µ–º 3D —Ç—è–ª–æ —Å –±–µ–∑–∫—Ä–∞–π–Ω–∞ 2D-—Ä–∞–≤–Ω–∏–Ω–∞, –∞ 4D-–æ–±–µ–∫—Ç–∏ - —Å –±–µ–∑–∫—Ä–∞–π–Ω–æ 3D - —Ö–∏–ø–µ—Ä—Ä–∞–≤–Ω–∏–Ω–∞. –ù–µ –±–∏—Ö–º–µ –º–æ–≥–ª–∏ –¥–∞ —Ä–∞–∑—Ä–µ–∂–µ–º 4D-–æ–±–µ–∫—Ç–∏ —Å –æ–±–∏–∫–Ω–æ–≤–µ–Ω–∞ —Ä–∞–≤–Ω–∏–Ω–∞, –∫–∞–∫—Ç–æ –Ω–µ –º–æ–∂–µ–º –¥–∞ —Ä–∞–∑—Ä–µ–∂–µ–º —Å –ª–∏–Ω–∏—è 3D —Ç–µ–ª–∞, –º–æ–∂–µ–º –¥–∞ –≥–∏ "–ø—Ä–æ–±–∏–µ–º".
–Ý–∞–∑–≥—Ä—ä–≤–∫–∞
| –ö–∞–∫ –¥–∞ —Å–∏ —Å–≥–ª–æ–±–∏–º —Ç–µ—Å–µ—Ä–∞–∫—Ç? –í—Å–µ–∫–∏ –º–æ–∂–µ –¥–∞ —Å–∏ –Ω–∞–ø—Ä–∞–≤–∏ –∫—É–±, –∞ –µ—Ç–æ –∫–∞–∫ —Ç—Ä—è–±–≤–∞ –¥–∞ —Å–µ —Å–≥—ä–Ω–µ —Ç–µ—Å–µ—Ä–∞–∫—Ç: –û–ø–∏—Ç–∞–π—Ç–µ —Å–µ –≤–Ω–∏–º–∞—Ç–µ–ª–Ω–æ –¥–∞ –∑–∞–ª–µ–ø–∏—Ç–µ –µ–¥–Ω–æ—Ü–≤–µ—Ç–Ω–∏—Ç–µ —Å—Ç—Ä–∞–Ω–∏ –Ω–∞ –∫—É–±–æ–≤–µ—Ç–µ –∫–∞–∫—Ç–æ –µ –ø–æ–∫–∞–∑–∞–Ω–æ, –∫–∞—Ç–æ –Ω–µ –∑–∞–±—Ä–∞–≤—è—Ç–µ, —á–µ —ä–≥–ª–∏—Ç–µ –æ—Å—Ç–∞–≤–∞—Ç –ø—Ä–∞–≤–∏, –∞ –∫—É–±–æ–≤–µ—Ç–µ –Ω–µ –±–∏–≤–∞ –¥–∞ —Å–µ –¥–µ—Ñ–æ—Ä–º–∏—Ä–∞! –£—Å–ø—è—Ö—Ç–µ –ª–∏? | 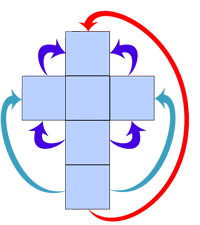 |
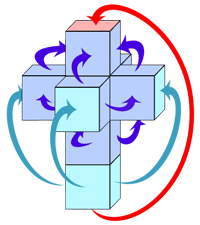 |
¬Ý–¢–æ–∑–∏ –º–æ–¥–µ–ª –Ω–∞ —Ç–µ—Å–µ—Ä–∞–∫—Ç –µ —Ç–æ–ª–∫–æ–≤–∞ —Ç–æ—á–µ–Ω –∏ –±–ª–∏–∑—ä–∫ –¥–æ —Ç–æ–≤–∞, –∫–æ–µ—Ç–æ –µ –≤ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª–Ω–æ—Å—Ç, –∫–æ–ª–∫–æ—Ç–æ —Ç–∞–∑–∏ –ø—Ä–æ–µ–∫—Ü–∏—è –Ω–∞ –∫—É–± –≤—ä—Ä—Ö—É –ª–∏—Å—Ç.
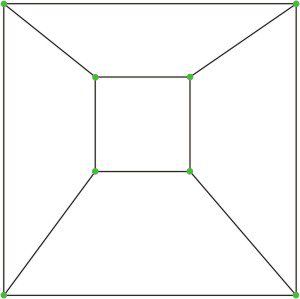
–ù–æ —Å–ø–µ—Ü–∏–∞–ª–Ω–æ —Å –ø—Ä–æ–µ–∫—Ü–∏–∏—Ç–µ —â–µ —Å–µ –∑–∞–ø–æ–∑–Ω–∞–µ–º –≤ –¥—Ä—É–≥–∞ —Ç–µ–º–∞.
–£—Å–ø–æ—Ä–µ–¥–Ω–∞ –ø—Ä–æ–µ–∫—Ü–∏—è
–í—Å–µ–∫–∏ –æ–±–µ–∫—Ç —Å N+1 —Ä–∞–∑–º–µ—Ä–Ω–æ—Å—Ç —Å–µ –æ–±—Ä–∞–∑—É–≤–∞ –æ—Ç N-–º–µ—Ä–µ–Ω –∫–∞—Ç–æ —Å–µ —Ç—Ä–∞–Ω—Å–ª–∏—Ä–∞, –Ω–∞—Ä–∞—Å–Ω–µ¬Ý(–µ–∫—Å—Ç—Ä—É–¥–Ω–µ - –Ω–µ –º–æ–≥–∞ –¥–∞ –Ω–∞–º–µ—Ä—è —Ç–æ—á–µ–Ω –ø—Ä–µ–≤–æ–¥ –Ω–∞ –¥—É–º–∞—Ç–∞ extrude) –≤ N+1 –ø–æ—Å–æ–∫–∞ (–≤–∏–∂—Ç–µ —Ç–∞–±–ª–∏—á–∫–∞—Ç–∞ —Å –∞–Ω–∞–ª–æ–≥–∏–∏—Ç–µ).
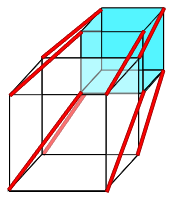
–°—ä—â–æ—Ç–æ –µ –∏ —Å 4D-–æ–±–µ–∫—Ç–∞, –Ω–∞–ø—Ä–∏–º–µ—Ä —Ç–µ—Å–µ—Ä–∞–∫—Ç–∞ (—Ö–∏–ø–µ—Ä–∫—É–±–∞), —Å–∞–º–æ –¥–µ—Ç–æ –Ω–∏ –µ –º–∞–ª–∫–æ —Ç—Ä—É–¥–Ω–æ –¥–∞ –≥–æ –æ—Å—ä–∑–Ω–∞–µ–º —Å —Ä–∞–∑—É–º–∞ —Å–∏ - –≤–∑–µ–º–∞–º–µ –µ–¥–∏–Ω –∫—É–± —Å—ä—Å —Å—Ç—Ä–∞–Ω–∞ L, –µ–∫—Å—Ç—Ä—É–¥–≤–∞–º–µ –≥–æ –ø–æ –Ω–∞–ø—Ä–∞–≤–ª–µ–Ω–∏–µ –Ω–∞ 4-—Ç–∞—Ç–∞ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–Ω–∞ –æ—Å W –∏ –ø–æ–ª—É—á–∞–≤–∞–º–µ —Ç–µ—Å–µ—Ä–∞–∫—Ç —Å –æ–±–µ–º L4.
"–û–≥—Ä–∞–¥–µ–Ω" –µ –æ—Ç 8 —Å—Ç–µ–Ω–∏-—Ç–µ–ª–∞ —Å –æ–±–µ–º L3. –¢–æ—á–Ω–æ –∫–∞—Ç–æ –∫—É–±–∞ –∏ –∫–≤–∞–¥—Ä–∞—Ç–∞, –≤—Å–∏—á–∫–∏ —Ä—ä–±–æ–≤–µ –≤ —Ä–∞–º–∫–∏—Ç–µ –Ω–∞ –µ–¥–∏–Ω —Ç–µ—Å–µ—Ä–∞–∫—Ç —Å–∞ —Å –µ–¥–Ω–∞–∫–≤–∞ –¥—ä–ª–∂–∏–Ω–∞ –∏ –≤—Å–∏—á–∫–∏ –æ—Ç —ä–≥–ª–∏—Ç–µ —Å–∞ –ø–æ–¥ –ø—Ä–∞–≤ —ä–≥—ä–ª. ¬Ý
–ö–∞—Ä–ª –°–µ–π–≥—ä–Ω –∑–∞¬Ý4D-–ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ—Ç–æ
–ê–∫–æ –æ—â–µ –Ω–µ —Å—Ç–µ "—É—Å–µ—Ç–∏–ª–∏" –∫–∞–∫–≤–æ –µ 4-—Ç–æ –∏–∑–º–µ—Ä–µ–Ω–∏–µ, –∏–∑–≥–ª–µ–¥–∞–π—Ç–µ –∏ —Ç–æ–≤–∞ —Ñ–∏–ª–º—á–µ, –≤ –∫–æ–µ—Ç–æ –ö–∞—Ä–ª –°–µ–π–≥—ä–Ω —Å–µ –æ–ø–∏—Ç–≤–∞ –¥–∞ –¥–∞–¥–µ —Ä–∞–∑–±–∏—Ä–∞–Ω–µ –Ω–∞ —Ç–∞–∑–∏ –Ω–µ–ø–æ—Å–∏–ª–Ω–∞ –∑–∞ —Ä–∞–∑—É–º–∞ –Ω–∏ –≥–ª–∞–≤–æ–±–ª—ä—Å–∫–∞–Ω–∏—Ü–∞.
–° —Ç–æ–≤–∞ –Ω–µ –∑–∞–≤—ä—Ä—à–≤–∞—Ç —É—Å–∏–ª–∏—è—Ç–∞ –Ω–∏ –¥–∞ —Å–µ —Ä–∞–∑—Ö–æ–¥–∏–º –≤ –ø–æ-–≤–∏—Å—à–∏—Ç–µ –∏–∑–º–µ—Ä–µ–Ω–∏—è. –í —Å–ª–µ–¥–≤–∞—â–∞—Ç–∞ —Ç–µ–º–∞ —â–µ –≤–∏ –∑–∞–ø–æ–∑–Ω–∞–µ–º —Å –æ—â–µ –Ω–∞—á–∏–Ω–∏ (–ø—Ä–æ–µ–∫—Ü–∏–∏, –∑–∞–≤—ä—Ä—Ç–∞–Ω–∏—è, –æ–±–≤–∏–≤–∫–∏) –∏ —Ç—ä–ª–∫—É–≤–∞–Ω–∏—è.
–ò–∑—Ç–æ—á–Ω–∏—Ü–∏:
wikipedia-Four-dimensional space
Introduction to the fourth dimension






















–ö–æ–º–µ–Ω—Ç–∞—Ä–∏
–ú–æ–ª—è, —Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–∞–π—Ç–µ —Å–µ –æ—Ç T–£–ö!
–ê–∫–æ –≤–µ—á–µ –∏–º–∞—Ç–µ —Ä–µ–≥–∏—Å—Ç—Ä–∞—Ü–∏—è, –Ω–∞—Ç–∏—Å–Ω–µ—Ç–µ –¢–£–ö!
07.02 2015 –≤ 17:08
http://video.ketc.org/video/2365419242/
–ù–∞–ø—Ä–∞–≤–µ–Ω–æ –µ –æ—Ç –ò–≤–∞–Ω –•–æ—Ä–æ–∑–æ–≤ –æ—Ç —É–Ω–∏–≤–µ—Ä—Å–∏—Ç–µ—Ç–∞ –í–∞—à–∏–Ω–≥—Ç–æ–Ω –≤ –°–µ–π–Ω—Ç –õ—É–∏—Å, –ú–∏—Å—É—Ä–∏. –í–∏–¥–µ–æ—Ç–æ –µ –æ—Ç –∏–Ω—Ç–µ—Ä–≤—é, –ø–æ–∫–∞–∑–∞–Ω–æ –ø–æ —Ç–µ–ª–µ–≤–∏–∑–∏—è—Ç–∞.
–ü–æ—Å–ª–µ–¥–Ω–∏ –∫–æ–º–µ–Ω—Ç–∞—Ä–∏
4I4ATA
–ù–æ–≤, —Å–∫—Ä–∏—Ç –¥–æ—Å–µ–≥–∞ –≤—Ö–æ–¥ –≤ –ø–∏—Ä–∞–º–∏–¥–∞—Ç–∞ –Ω–∞ –ú–∏–∫–µ—Ä–∏–Ω –µ –æ—Ç–∫—Ä–∏—Ç –ø–æ –∞–Ω–æ–º–∞–ª–∏–∏ –ø—Ä–∏ —Å–∫–∞–Ω–∏—Ä–∞–Ω–µ
YKoshev
–ü—Ä–µ—Å—Ç–∏–∂–Ω–∞ –Ω–∞–≥—Ä–∞–¥–∞ –æ—Ç –ë–ê–ù —Å–ø–µ—á–µ–ª–∏ –≥–ª–∞–≤–Ω–∏—è—Ç —Ä–µ–¥–∞–∫—Ç–æ—Ä –Ω–∞ –ù–∞—É–∫–∞OFFNews
Johnny B Goode
–ü—Ä–µ—Å—Ç–∏–∂–Ω–∞ –Ω–∞–≥—Ä–∞–¥–∞ –æ—Ç –ë–ê–ù —Å–ø–µ—á–µ–ª–∏ –≥–ª–∞–≤–Ω–∏—è—Ç —Ä–µ–¥–∞–∫—Ç–æ—Ä –Ω–∞ –ù–∞—É–∫–∞OFFNews
Gunteer
–ü—Ä–µ—Å—Ç–∏–∂–Ω–∞ –Ω–∞–≥—Ä–∞–¥–∞ –æ—Ç –ë–ê–ù —Å–ø–µ—á–µ–ª–∏ –≥–ª–∞–≤–Ω–∏—è—Ç —Ä–µ–¥–∞–∫—Ç–æ—Ä –Ω–∞ –ù–∞—É–∫–∞OFFNews
–•—Ä–∏—Å—Ç–∏—è–Ω–∏–Ω
–¢–æ–≤–∞ –µ –∫—Ä–∞–ª—è—Ç –Ω–∞ —Ç–∏–∫–≤–∏—Ç–µ: –¢–∏–∫–≤–∞—Ç–∞ –º—É —Ç–µ–∂–∏ –Ω–∞–¥ –µ–¥–∏–Ω –µ–¥–∏–Ω —Ç–æ–Ω