

–ē–ī–Ĺ–į –ĺ—ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ł—ā–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł –≤ –ē–≤–ļ–Ľ–ł–ī–ĺ–≤–į—ā–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ķ —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –∑–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ī–≤–Ķ —ā–ĺ—á–ļ–ł: S12=(x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 , –ļ–ĺ—Ź—ā–ĺ –Ķ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–Ĺ–į –Ņ—Ä–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ĺ –≤—ä—Ä—ā–Ķ–Ĺ–Ķ –ł –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į. –ź–Ĺ–į–Ľ–ĺ–≥—ä—ā –Ļ –Ņ—Ä–ł –õ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –Ķ S12= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 + (u2 - u1 )2, –ļ—ä–ī–Ķ—ā–ĺ u2 = i.c.t2 –ł u1 = i.c.1 , –ļ—ä–ī–Ķ—ā–ĺ i2=-1. –Ę–į–∑–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –Ķ —Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ī–≤–Ķ —ā–ĺ—á–ļ–ł –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ –ł –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –Ķ —Ā—ä—Č–ĺ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–Ĺ–į –∑–į –õ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł. –í—Ä–Ķ–ľ–Ķ—ā–ĺ —ā—É–ļ —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź –Ņ–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ĺ –ļ–į—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ. –ü—ä—Ä–≤–ł—Ź—ā, –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –ļ–į—ā–ĺ —Ä–į–≤–Ĺ–ĺ–Ņ—Ä–į–≤–Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į –Ķ –Ķ–ī–ł–Ĺ –ĺ—ā –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ—Ź—ā –Ĺ–į –ź–Ļ–Ĺ—Č–į–Ļ–Ĺ –≤ –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –≤ –¶—é—Ä–ł—Ö, –•–Ķ—Ä–ľ–į–Ĺ –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł. –ü—Ä–Ķ–∑ 1908 –≥. –ł–∑–Ĺ–į—Ā—Ź –Ľ–Ķ–ļ—Ü–ł—Ź –∑–į —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –∑–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į —Ā –ī—É–ľ–ł—ā–Ķ:
"–ě—ā—Ā–Ķ–≥–į –Ĺ–į—ā–į—ā—ä–ļ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ —Ā–į–ľ–ĺ –Ņ–ĺ —Ā–Ķ–Ī–Ķ —Ā–ł –ł –≤—Ä–Ķ–ľ–Ķ—ā–ĺ —Ā–į–ľ–ĺ –Ņ–ĺ —Ā–Ķ–Ī–Ķ —Ā–ł —Ā–į –ĺ–Ī—Ä–Ķ—á–Ķ–Ĺ–ł –ī–į —É–≥–į—Ā–Ĺ–į—ā –ļ–į—ā–ĺ —Ā–Ķ–Ĺ–ļ–ł –ł —Ā–į–ľ–ĺ —Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ—ā–ĺ –ĺ–Ī–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī–≤–Ķ—ā–Ķ —Č–Ķ –∑–į–Ņ–į–∑–ł –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–į —Ä–Ķ–į–Ľ–Ĺ–ĺ—Ā—ā"
–ź–ļ–ĺ –Ĺ–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –Ņ—Ä–ł–Ņ–ł—Ā–≤–į–ľ–Ķ –ĺ—Ā–≤–Ķ–Ĺ —ā—Ä–ł—ā–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł x , y , z –ł –≤—Ä–Ķ–ľ–Ķ—ā–ĺ t , —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ĺ –Ņ–ĺ i.c , —ā–ĺ –Ņ–ĺ–Ľ—É—á–į–≤–į–ľ–Ķ —Ą–ĺ—Ä–ľ–į–Ľ–Ĺ–ĺ —ā–ĺ—á–ļ–į –≤ —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ (–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł), –≤ –ļ–ĺ–Ķ—ā–ĺ —ā–ĺ—á–ļ–ł—ā–Ķ –ł–ľ–į—ā –≤–Ķ—á–Ķ —á–Ķ—ā–ł—Ä–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł: x , y , z , i.c.t –ł–Ľ–ł x , y , z , u. –í—Ā—Ź–ļ–į —ā–į–ļ–į–≤–į "—ā–ĺ—á–ļ–į" –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į—Ä–Ķ—á–Ķ —Ā—ä–Ī–ł—ā–ł–Ķ. –ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ—ä—ā –ľ–Ķ–∂–ī—É –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –≤ —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ķ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–Ķ–Ĺ –Ņ—Ä–ł –Ņ—Ä–Ķ—Ö–ĺ–ī –ĺ—ā –Ķ–ī–Ĺ–į –ł–Ĺ–Ķ—Ä—Ü–ł–į–Ľ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į –≤ –ī—Ä—É–≥–į.
–ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ-–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –ľ–Ķ–∂–ī—É —Ā—ä–Ī–ł—ā–ł—Ź—ā–į
–ė–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł
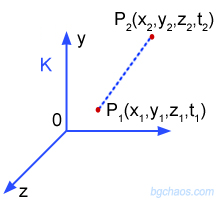 –Ě–Ķ–ļ–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł x1 , y1 , z1 , u1 –ł x2 , y2 , z2 , u2 –≤ —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į K. –ü—ä—Ä–≤–ĺ—ā–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ –Ķ –ī–į —Ä–Ķ—á–Ķ–ľ –ł–∑—Ā—ā—Ä–Ķ–Ľ —Ā –ĺ—Ä—ä–ī–ł–Ķ –≤ —ā–ĺ—á–ļ–į —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā , –į –≤—ā–ĺ—Ä–ĺ—ā–ĺ - –Ņ–į–ī–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā–Ĺ–į—Ä—Ź–ī–į –≤ —ā–ĺ—á–ļ–į –ł –ľ–ĺ–ľ–Ķ–Ĺ—ā . –Ę–ĺ–≥–į–≤–į –∑–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –ľ–Ķ–∂–ī—É —ā–Ķ–∑–ł –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–Ņ–ł—ą–Ķ–ľ: S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 + (u2 - u1 )2 , –ł–Ľ–ł S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2, –Ņ–ĺ–Ĺ–Ķ–∂–Ķ c2.t2 = x2 + y2 + z2 (–Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –∑–į —Ā—Ą–Ķ—Ä–į - (—Ā—Ą–Ķ—Ä–į —Ā –ī–ł–į–ľ–Ķ—ā—ä—Ä —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ī–ł –ł–∑–ľ–ł–Ĺ–į–Ľ —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –∑–į –≤—Ä–Ķ–ľ–Ķ t ), —ā–ĺ x2 + y2 + z2 - c2.t2 = 0 , —ā.–Ķ. –∑–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –ł–ľ–į–ľ–Ķ:
–Ě–Ķ–ļ–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł x1 , y1 , z1 , u1 –ł x2 , y2 , z2 , u2 –≤ —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į K. –ü—ä—Ä–≤–ĺ—ā–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ –Ķ –ī–į —Ä–Ķ—á–Ķ–ľ –ł–∑—Ā—ā—Ä–Ķ–Ľ —Ā –ĺ—Ä—ä–ī–ł–Ķ –≤ —ā–ĺ—á–ļ–į —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā , –į –≤—ā–ĺ—Ä–ĺ—ā–ĺ - –Ņ–į–ī–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā–Ĺ–į—Ä—Ź–ī–į –≤ —ā–ĺ—á–ļ–į –ł –ľ–ĺ–ľ–Ķ–Ĺ—ā . –Ę–ĺ–≥–į–≤–į –∑–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –ľ–Ķ–∂–ī—É —ā–Ķ–∑–ł –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–Ņ–ł—ą–Ķ–ľ: S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 + (u2 - u1 )2 , –ł–Ľ–ł S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2, –Ņ–ĺ–Ĺ–Ķ–∂–Ķ c2.t2 = x2 + y2 + z2 (–Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –∑–į —Ā—Ą–Ķ—Ä–į - (—Ā—Ą–Ķ—Ä–į —Ā –ī–ł–į–ľ–Ķ—ā—ä—Ä —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ī–ł –ł–∑–ľ–ł–Ĺ–į–Ľ —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –∑–į –≤—Ä–Ķ–ľ–Ķ t ), —ā–ĺ x2 + y2 + z2 - c2.t2 = 0 , —ā.–Ķ. –∑–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –ł–ľ–į–ľ–Ķ:
S122—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á= 0
–Ē–į, –Ĺ–ĺ –ļ–į–ļ—ā–ĺ –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–ĺ—ā–ĺ (–ł–∑—Ā—ā—Ä–Ķ–Ľ —Ā –ĺ—Ä—ä–ī–ł–Ķ), —ā–į–ļ–į –ł –Ņ–ĺ–≤–Ķ—á–Ķ—ā–ĺ —Ā—ä–Ī–ł—ā–ł—Ź –Ĺ–Ķ —Ā—ā–į–≤–į—ā —Ā—ä—Ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į, —ā–ĺ–≥–į–≤–į S122 ‚Ȇ 0 –ł –∑–į—Č–ĺ—ā–ĺ c2(t2 - t1 )2 –Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–ĺ –ĺ—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ĺ—Ä—ä–ī–ł–Ķ—ā–ĺ –ł –Ņ–ĺ–Ņ–į–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ: (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2, —ā–ĺ —ā–ĺ–≥–į–≤–į
S122 < 0 ., —ā.–Ķ. —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –Ķ –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į.
–ź–ļ–ĺ —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź - –ł–∑—Ā—ā—Ä–Ķ–Ľ–į —Ā –ĺ—Ä—ä–ī–ł–Ķ –ł –Ņ–į–ī–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā–Ĺ–į—Ä—Ź–ī–į - —Ā–Ņ—Ä—Ź–ľ–ĺ –ī—Ä—É–≥–į—ā–į –ł–Ĺ–Ķ—Ä—Ü–ł–į–Ľ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į K' –į–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –ľ–ĺ–∂–Ķ–ľ –ī–į –∑–į–Ņ–ł—ą–Ķ–ľ:
S'122= (x'2 - x'1 )2 + (y'2 - y'1 )2 + (z'2 - z'1 )2 + (u'2 - u'1 )2 , –ł–Ľ–ł
S'122= (x'2 - x'1 )2 + (y'2 - y'1 )2 + (z'2 - z'1 )2 - c2(t'2 - t'1 )2,
–į–ļ–ĺ –∑–į–ľ–Ķ—Ā—ā–ł–ľ —Ā x'1 , x'2 ... –ľ–Ķ—Ā—ā–į—ā–į –Ĺ–į x1 , x2 ... —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –Ľ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł. –Ę–ĺ–≥–į–≤–į –ł–ľ–į –ľ—Ź—Ā—ā–ĺ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ—ā–ĺ:
S'122=S122 –ł–Ľ–ł S'12=S12.
–Ę–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ī–≤–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ł —Ā—ä–Ī–ł—ā–ł—Ź –Ķ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į , –Ĺ–Ķ–ł–∑–ľ–Ķ–Ĺ–Ĺ–į –Ņ—Ä–ł –Ņ—Ä–Ķ—Ö–ĺ–ī –ĺ—ā K –ļ—ä–ľ K'. –ú–Ķ–∂–ī—É –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –ĺ—ā —Ä–ĺ–ī–į –Ĺ–į –ł–∑—Ā—ā—Ä–Ķ–Ľ –ĺ—ā –ĺ—Ä—ä–ī–ł–Ķ –ł –Ņ–ĺ–Ņ–į–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –ľ—É, —Ä–į–∂–ī–į–Ĺ–Ķ –Ĺ–į —á–ĺ–≤–Ķ–ļ–į –ł –Ĺ–Ķ–≥–ĺ–≤–į—ā–į —Ā–ľ—ä—Ä—ā, —ā.–Ķ. –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ- —Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–į –≤—Ä—ä–∑–ļ–į, —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ–Ķ–Ĺ–ł–Ķ –≤—ä–≤ –≤—Ā—Ź–ļ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į –Ķ –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į: S122 < 0 .
–†–Ķ–į–Ľ–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł
–í—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ľ–ł –Ķ —ā–ĺ–≤–į "—Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ" –ī–į –Ķ —Ä–Ķ–į–Ľ–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, S122 > 0 ? –Ē–į! –Ē–į —Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ, —á–Ķ –Ĺ–į –°–Ľ—ä–Ĺ—Ü–Ķ—ā–ĺ –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā t1 —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –Ņ–Ķ—ā–Ĺ–ĺ —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł x1 , y1 , z1. –í –ľ–ĺ–ľ–Ķ–Ĺ—ā t2 –į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ –Ĺ–į—Ā–ĺ—á–≤–į —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–į —Ā–ł –ļ—ä–ľ –°–Ľ—ä–Ĺ—Ü–Ķ—ā–ĺ –≤ –ĺ–Ī—Ā–Ķ—Ä–≤–į—ā–ĺ—Ä–ł—Ź —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł: x2 , y2 , z2. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł—ā–Ķ –ł –≤—Ä–Ķ–ľ–Ķ—ā–ĺ —Ā–į –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł –≤ –Ķ–ī–Ĺ–į –ĺ—ā–Ņ—Ä–į–≤–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į, –ī–į —Ä–Ķ—á–Ķ–ľ –ó–Ķ–ľ—Ź—ā–į. –ó–į –ī–į –ī–ĺ—Ā—ā–ł–≥–Ĺ–Ķ —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –ĺ—ā –°–Ľ—ä–Ĺ—Ü–Ķ—ā–ĺ –ī–ĺ –ó–Ķ–ľ—Ź—ā–į —Ā–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł 500—Ā–Ķ–ļ.. –ź–ļ–ĺ t2 - t1 < 500—Ā–Ķ–ļ., —ā–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ—ā–ĺ –Ĺ–į –į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ā–ľ—Ź—ā–į –ļ–į—ā–ĺ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ –ĺ—ā –Ņ–ĺ—Ź–≤–į—ā–į –Ĺ–į –Ņ–Ķ—ā–Ĺ–ĺ—ā–ĺ, –∑–į—Č–ĺ—ā–ĺ –ļ–ĺ–≥–į—ā–ĺ –Ķ –Ĺ–į—Ā–ĺ—á–ł–Ľ —ā–Ķ–Ľ–Ķ—Ā–ļ–ĺ–Ņ–į —Ā–ł –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā t2, —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į –ĺ—ā –Ņ–Ķ—ā–Ĺ–ĺ—ā–ĺ –ĺ—Č–Ķ –Ĺ–Ķ –Ķ –ī–ĺ—Ā—ā–ł–≥–Ĺ–į–Ľ–į –ó–Ķ–ľ—Ź—ā–į.
–ź–ļ–ĺ –≤—ä–≤–Ķ–ī–Ķ–ľ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ĺ—ā –°–Ľ—ä–Ĺ—Ü–Ķ—ā–ĺ –ī–ĺ –ó–Ķ–ľ—Ź—ā–į –ł–ľ–į–ľ–Ķ:
d122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2=(150 000 000km)2
–ł –į–ļ–ĺ c2(t2 - t1 )2< (150 000 000km)2, —ā–ĺ S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2 > 0 , —ā.–Ķ. S122 > 0 , –į S12 —Ā–ł –Ķ —Ä–Ķ–į–Ľ–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, –į —ā–į–ļ–ł–≤–į –ľ–ĺ–∂–Ķ –ī–į —Ā–į –ľ–Ĺ–ĺ–≥–ĺ —Ā—ä–Ī–ł—ā–ł—Ź, –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –Ĺ–į –ĺ–Ņ–ł—Ā–į–Ĺ–ĺ—ā–ĺ.
–ě—ā –Ĺ–į–Ņ–ł—Ā–į–Ĺ–ĺ—ā–ĺ –ī–ĺ —ā—É–ļ —Ā–Ķ –≤–ł–∂–ī–į –ļ–ĺ–Ľ–ļ–ĺ –≤–į–∂–Ĺ–į –Ķ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į - —ā—Ź —Ä–Ķ—ą–į–≤–į –ļ–ĺ–Ķ –Ķ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ –ł –ļ–ĺ–Ķ - –Ĺ–Ķ. –ė —ā–ĺ–≤–į –Ķ —ā–į–ļ–į, –∑–į—Č–ĺ—ā–ĺ —ā—Ź –Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ–Ĺ–į—ā–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā –ł –Ĺ–į –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź—ā–į, —ā.–Ķ –ī–į —Ā–Ķ –ł–∑–≤—ä—Ä—ą–ł –Ĺ—Ź–ļ–į–ļ–≤–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ, —ā.–Ķ. –ī–į —Ā–Ķ –Ņ—Ä–ł—á–ł–Ĺ–ł –Ĺ—Ź–ļ–į–ļ–≤–ĺ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ. –ó–į—ā–ĺ–≤–į –ł –Ņ–ĺ—Ā—ā–ł–≥–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł –Ĺ–į–ī —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ĺ–į—ā–į –ĺ–∑–Ĺ–į—á–į–≤–į —Ä–į–∑—Ä—É—ą–į–≤–į–Ĺ–Ķ –Ĺ–į –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–į—ā–į –≤—Ä—ä–∑–ļ–į.
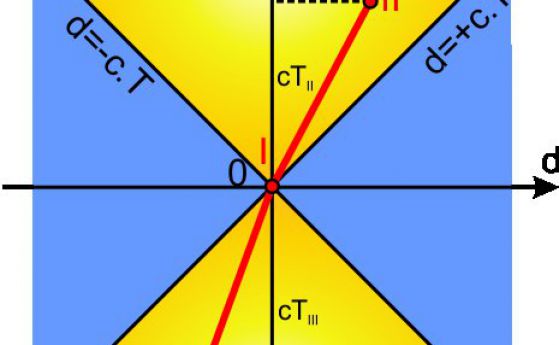
–ď—Ä–į—Ą–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ
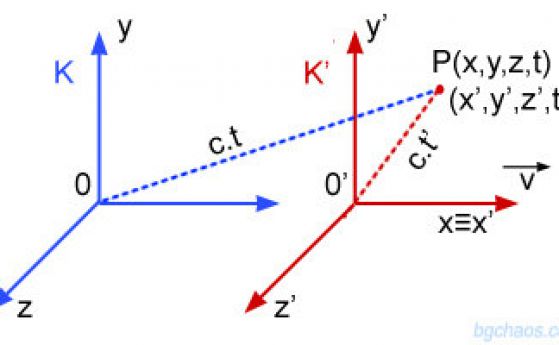
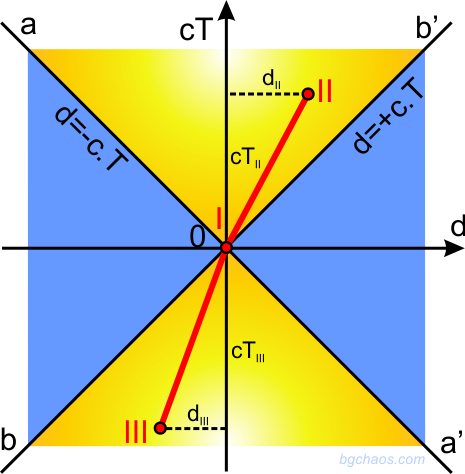 –õ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ł–∑–ĺ–Ī—Ä–į–∑–Ķ–Ĺ–ł –≥—Ä–į—Ą–ł—á–Ĺ–ĺ –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ-–≤—Ä–Ķ–ľ–Ķ–≤–į –ī–ł–į–≥—Ä–į–ľ–į¬†–Ĺ–į¬†–ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł. –ú–į–ļ–į—Ä –ł —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ł –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ –ļ–į—ā–ĺ –Ĺ–į —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–į—ā–į –ĺ—Ā —Ā–Ķ –ĺ—ā–Ľ–ĺ–∂–į—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ł—ā–Ķ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –į –Ņ–ĺ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–į—ā–į - –≤—Ä–Ķ–ľ–Ķ–≤–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł. –ź–ļ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –Ņ—Ä–į–≤–ł—ā–Ķ: d = +cT –ł d = -cT, –≤—Ā–ł—á–ļ–ł —Ā—ä–Ī–ł—ā–ł—Ź, –Ľ–Ķ–∂–į—Č–ł –≤—ä—Ä—Ö—É —ā–Ķ–∑–ł –Ņ—Ä–į–≤–ł —Ā–į –ĺ—ā –≥—Ä–į–Ĺ–ł—á–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ. –Ę–Ķ–∑–ł –Ņ—Ä–į–≤–ł –ĺ–Ī—Ä–į–∑—É–≤–į—ā —ā.–Ĺ. "—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –ļ–ĺ–Ĺ—É—Ā"
–õ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ł–∑–ĺ–Ī—Ä–į–∑–Ķ–Ĺ–ł –≥—Ä–į—Ą–ł—á–Ĺ–ĺ –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ-–≤—Ä–Ķ–ľ–Ķ–≤–į –ī–ł–į–≥—Ä–į–ľ–į¬†–Ĺ–į¬†–ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł. –ú–į–ļ–į—Ä –ł —á–Ķ—ā–ł—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ł –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ –ļ–į—ā–ĺ –Ĺ–į —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–į—ā–į –ĺ—Ā —Ā–Ķ –ĺ—ā–Ľ–ĺ–∂–į—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ł—ā–Ķ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –į –Ņ–ĺ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–į—ā–į - –≤—Ä–Ķ–ľ–Ķ–≤–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł. –ź–ļ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –Ņ—Ä–į–≤–ł—ā–Ķ: d = +cT –ł d = -cT, –≤—Ā–ł—á–ļ–ł —Ā—ä–Ī–ł—ā–ł—Ź, –Ľ–Ķ–∂–į—Č–ł –≤—ä—Ä—Ö—É —ā–Ķ–∑–ł –Ņ—Ä–į–≤–ł —Ā–į –ĺ—ā –≥—Ä–į–Ĺ–ł—á–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ. –Ę–Ķ–∑–ł –Ņ—Ä–į–≤–ł –ĺ–Ī—Ä–į–∑—É–≤–į—ā —ā.–Ĺ. "—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –ļ–ĺ–Ĺ—É—Ā"
. –ü—Ä–ł–Ķ–ľ–į–ľ–Ķ —Ā—ä–Ī–ł—ā–ł–Ķ I –∑–į –Ĺ–į—á–į–Ľ–Ĺ–ĺ –≤ —ā.0. –ó–į —Ā—ä–Ī–ł—ā–ł–Ķ II, –ļ–ĺ–Ķ—ā–ĺ –Ľ–Ķ–∂–ł –≤—ä—ā—Ä–Ķ –≤ –≥–ĺ—Ä–Ĺ–ł—Ź –ļ–ĺ–Ĺ—É—Ā –ĘII >0 (t2 < t1), –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ —Ā—ä–Ī–ł—ā–ł–Ķ II —Ā–Ķ —Ā–Ľ—É—á–≤–į —Ā–Ľ–Ķ–ī —Ā—ä–Ī–ł—ā–ł–Ķ I. –ď–ĺ—Ä–Ĺ–į—ā–į —Ą—É–Ĺ–ł—Ź –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ĺ–ł—Ź –ļ–ĺ–Ĺ—É—Ā a0b' –Ķ –∑–ĺ–Ĺ–į—ā–į –Ĺ–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—ā–ĺ –Ī—ä–ī–Ķ—Č–Ķ. –í –ī–ĺ–Ľ–Ĺ–ł—Ź "—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –ļ–ĺ–Ĺ—É—Ā" —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į —Ā—ä–Ī–ł—ā–ł–Ķ III, –∑–į –ļ–ĺ–Ķ—ā–ĺ –ĘIII <0 , —ā–ĺ–Ķ—Ā—ā t2 < t1, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ —Ā—ä–Ī–ł—ā–ł–Ķ III —Ā–Ķ –Ķ —Ā–Ľ—É—á–ł–Ľ–ĺ –Ņ—Ä–Ķ–ī–ł —Ā—ä–Ī–ł—ā–ł–Ķ I. –Ē–ĺ–Ľ–Ĺ–ł—Ź—ā "—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –ļ–ĺ–Ĺ—É—Ā" a'0b –Ķ –∑–ĺ–Ĺ–į—ā–į –Ĺ–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—ā–ĺ –ľ–ł–Ĺ–į–Ľ–ĺ.
–ó–į –≤—Ā–Ķ–ļ–ł –ī–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ —Ā—ä—Ā—ā–į–≤—Ź —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –ļ–ĺ–Ĺ—É—Ā –ļ–į—ā–ĺ –Ķ–ī–Ĺ–ĺ –ĺ—ā —ā—Ź—Ö –Ņ—Ä–ł–Ķ–ľ–į–ľ–Ķ –∑–į –Ĺ–į—á–į–Ľ–Ĺ–ĺ –ł –Ņ–ĺ—Ā—ā–į–≤—Ź–ľ–Ķ –Ĺ–į –≤—ä—Ä—Ö–į –Ĺ–į –ļ–ĺ–Ĺ—É—Ā–į.
–ě–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—ā–Ķ —Ā I, II –ł III —ā–ĺ—á–ļ–ł, —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—Č–ł –Ĺ–į –Ĺ—Ź–ļ–į–ļ–≤–ł —Ā—ä–Ī–ł—ā–ł—Ź , —Ā–Ķ –Ĺ–į—Ä–ł—á–į—ā —Ā–≤–Ķ—ā–ĺ–≤–Ĺ–ł —ā–ĺ—á–ļ–ł.
–ü–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į –ĺ—ā —Ā—ä–Ī–ł—ā–ł—Ź, —Ā—ā–į–≤–į—Č–ł —Ā –Ķ–ī–Ĺ–į —á–į—Ā—ā–ł—Ü–į –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł —Ā–Ķ —Ā—ä–Ņ–ĺ—Ā—ā–į–≤—Ź —Ā –Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–į –Ľ–ł–Ĺ–ł—Ź, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į —Ā–≤–Ķ—ā–ĺ–≤–Ĺ–į –Ľ–ł–Ĺ–ł—Ź –Ĺ–į —á–į—Ā—ā–ł—Ü–į—ā–į. –ü—Ä–į–≤–į—ā–į I-II –Ķ —Ā–≤–Ķ—ā–ĺ–≤–Ĺ–į –Ľ–ł–Ĺ–ł—Ź –Ĺ–į —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ –ī–≤–ł–∂–Ķ—Č–į —Ā–Ķ —á–į—Ā—ā–ł—Ü–į —Ā—ä—Ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā dII/(cTII). –ź–ļ–ĺ —ā–ĺ—á–ļ–į—ā–į —Ā–Ķ –ī–≤–ł–∂–Ķ—ą–Ķ —Ā –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā —Č–Ķ—ą–Ķ –ī–į –ł–ľ–į –ļ—Ä–ł–≤–ĺ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–į —Ā–≤–Ķ—ā–ĺ–≤–Ĺ–į –Ľ–ł–Ĺ–ł—Ź. –°–≤–Ķ—ā–ĺ–≤–Ĺ–į—ā–į –Ľ–ł–Ĺ–ł—Ź –Ĺ–į –Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ–į —á–į—Ā—ā–ł—Ü–į –Ī–ł –ł–ľ–į–Ľ–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ d = 0, —ā–ĺ–Ķ—Ā—ā —ā—Ź —Č–Ķ —Ā—ä–≤–Ņ–į–ī–į —Ā –≤—Ä–Ķ–ľ–Ķ–≤–į—ā–į –ĺ—Ā. –°—ä–≤–ļ—É–Ņ–Ĺ–ĺ—Ā—ā—ā–į –ĺ—ā —ā–ĺ—á–ļ–ł –≤—ä—Ä—Ö—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–į—ā–į –ĺ—Ā d –ł–∑–ĺ–Ī—Ä–į–∑—Ź–≤–į –≤—Ā–ł—á–ļ–ł –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł —Ā—ä–Ī–ł—ā–ł—Ź –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ
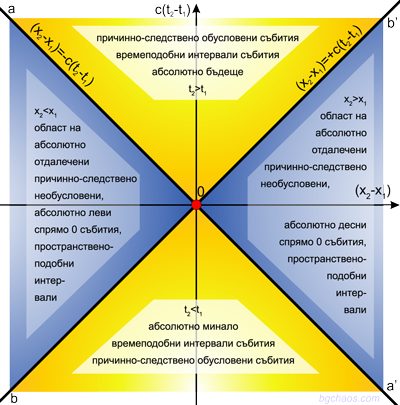
–Ę—Ä–ł –≥—Ä—É–Ņ–ł —Ā—ä–Ī–ł—ā–ł—Ź
–ė —ā–į–ļ–į, –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ 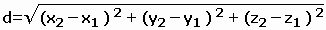 –ł –≤—Ä–Ķ–ľ–Ķ–≤–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ T = t2 - t1 , —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā —ā—Ä–ł –≥—Ä—É–Ņ–ł —Ā—ä–Ī–ł—ā–ł—Ź:
–ł –≤—Ä–Ķ–ľ–Ķ–≤–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ T = t2 - t1 , —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā —ā—Ä–ł –≥—Ä—É–Ņ–ł —Ā—ä–Ī–ł—ā–ł—Ź:
-
–ü—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ķ–Ĺ–ł
–ó–į –ī–į –Ī—ä–ī–Ķ –Ķ–ī–Ĺ–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ –Ņ—Ä–ł—á–ł–Ĺ–į –Ĺ–į –ī—Ä—É–≥–ĺ, —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–į –ł–∑–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ł –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į—ā–į:
d2< c2T2 (d< cT), S122 < 0
-
–ü—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ĺ –Ĺ–Ķ–ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ķ–Ĺ–ł
–Ē–≤–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —Ā–į –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ł –Ķ–ī–Ĺ–ĺ –ĺ—ā –ī—Ä—É–≥–ĺ, –į–ļ–ĺ:
d2 > c2T2 (d > cT), S122 > 0
-
–ď—Ä–į–Ĺ–ł—á–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ - —Ā—ä—Ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į
d2 = c2T2 (d = cT), S122 = 0
d = cT –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ—ā–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –ī–≤–Ķ —ā–ĺ—á–ļ–ł –Ķ —Ä–į–≤–Ĺ–ĺ –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ī–ł –ł–∑–ľ–ł–Ĺ–į–Ľ —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ķ–Ĺ –Ľ—ä—á –∑–į –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź.
–í—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł
–ź–ļ–ĺ —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ł–∑—Ä–į–∑–į: S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2, –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā —ā–ĺ–≤–į –ļ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā –Ņ—Ä–Ķ–ĺ–Ī–Ľ–į–ī–į–≤–į –≤ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –ľ–Ķ–∂–ī—É —ā–Ķ–∑–ł —Ā—ä–Ī–ł—ā–ł—Ź - –≤—Ä–Ķ–ľ–Ķ—ā–ĺ c2(t2 - t1 )2 –ł–Ľ–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2, –ł–ľ–į —Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł—ā–Ķ –Ĺ–į –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł.
-
–í—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł
(x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 < c2(t2 - t1 )2 ; S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2 < 0 ,
—ā.–Ķ. S122 < 0 , –į S12 –Ķ –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į.
-
–ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł
(x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 > c2(t2 - t1 )2 ; S122= (x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 - c2(t2 - t1 )2 > 0 ,
—ā.–Ķ. S122 > 0 , –į S12 –Ķ —Ä–Ķ–į–Ľ–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į.
-
–°–≤–Ķ—ā–Ľ–ł–Ĺ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł
(x2 - x1 )2 + (y2 - y1 )2 + (z2 - z1 )2 = c2(t2 - t1 )2 ; S122=0 ,
–Ę–ĺ–≤–į –Ķ –≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ –∑–į —á–į—Ā—ā–ł—Ü–ł, –ī–≤–ł–∂–Ķ—Č–ł —Ā–Ķ —Ā—ä—Ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –Ĺ–į —Ā–≤–Ķ—ā–Ľ–ł–Ĺ–į—ā–į. –ź–ļ–ĺ d=0, —ā.–Ķ. —Ā—ā–į–≤–į –≤—ä–Ņ—Ä–ĺ—Ā –∑–į –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ —ā—Ź–Ľ–ĺ, –ĺ—ā —ā–ĺ–≤–į —Ā–Ľ–Ķ–ī–≤–į, —á–Ķ S12=ic(t2-t1) –Ķ —á–ł—Ā—ā–ĺ –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –ł –∑–į–≤–ł—Ā–ł —Ā–į–ľ–ĺ –ĺ—ā –≤—Ä–Ķ–ľ–Ķ—ā–ĺ.
–ź–ļ–ĺ t2=t1 –ł–Ľ–ł —Ā—ä–Ī–ł—ā–ł—Ź—ā–į —Ā—ā–į–≤–į—ā –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ S12= d –ł –ł–ľ–į–ľ–Ķ —á–ł—Ā—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ. –Ě–ĺ d –Ķ –≤–ł–Ĺ–į–≥–ł —Ä–Ķ–į–Ľ–Ĺ–į, –ĺ—ā —ā–į–ľ –ł S12 , —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –ł–ľ–į–ľ–Ķ –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ķ–Ĺ–ł —Ā—ä–Ī–ł—ā–ł—Ź. –ė–∑–≤–ĺ–ī—ä—ā –Ķ, —á–Ķ –ī–≤–Ķ –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł —Ā—ä–Ī–ł—ā–ł—Ź –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–į –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ķ–Ĺ–ł –≤ –Ĺ–ł–ļ–ĺ—Ź –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į.
–õ—Ź–≤–ĺ –ł –ī—Ź—Ā–Ĺ–ĺ —Ā–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ł, –Ĺ–ĺ –Ņ—Ä–ł—á–ł–Ĺ–į—ā–į –≤–ł–Ĺ–į–≥–ł –Ķ –Ņ—Ä–Ķ–ī–ł —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ—ā–ĺ
–ź–ļ–ĺ (y2 - y1 )2 + (z2 - z1 )2 = (y'2 - y'1 )2 + (z'2 - z'1 )2 —Ā–Ľ–Ķ–ī–≤–į, —á–Ķ –į–ļ–ĺ S122=S'122 –ľ–ĺ–∂–Ķ –ī–į –∑–į–Ņ–ł—ą–Ķ–ľ (x2 - x1)2 - c2(t2 - t1)2 = (x'2 - x'1)2 - c2(t'2 - t'1)2.
–°—ä–≥–Ľ–į—Ā–Ĺ–ĺ –õ–ĺ—Ä–Ķ–Ĺ—Ü–ĺ–≤–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł:
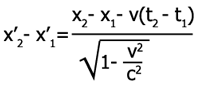
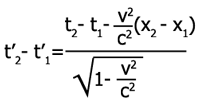
–Ě–Ķ–ļ–į –≤ —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į K, (t2 - t1) >0 –ł (x2 - x1 )>0 –ĺ—ā –Ņ—ä—Ä–≤–į—ā–į —Ą–ĺ—Ä–ľ—É–Ľ–į –ľ–ĺ–∂–Ķ –ī–į –Ĺ–į–Ņ—Ä–į–≤–ł–ľ —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ –ł–∑–≤–ĺ–ī–ł:
- –ź–ļ–ĺ (x2 - x1 )/(t2 - t1) > V , —ā–ĺ–≥–į–≤–į (x'2 - x'1) >0, —ā–ĺ–Ķ—Ā—ā –ł –≤ K'¬†–ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź –ł–ľ–į—ā –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ
- –ź–ļ–ĺ (x2 - x1 )/(t2 - t1) = V , —ā–ĺ (x'2 - x'1) =0 –ł–Ľ–ł –ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —Ā—ā–į–≤–į—ā –Ĺ–į –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ –ľ—Ź—Ā—ā–ĺ, —ā–ĺ–Ķ—Ā—ā K'¬†–Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā —ā—Ź–Ľ–ĺ—ā–ĺ, –ī–≤–ł–∂–Ķ—Č–ĺ —Ā–Ķ —Ā—ä—Ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā V
- –ź–ļ–ĺ (x2 - x1 )/(t2 - t1) < V , —ā–ĺ–≥–į–≤–į (x'2 - x'1) <0. –°–Ķ–≥–į –Ņ—ä—Ä–≤–ĺ—ā–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ –Ķ –ĺ—ā–ī—Ź—Ā–Ĺ–ĺ, –ī–ĺ–ļ–į—ā–ĺ –≤ K –Ī–Ķ—ą–Ķ –ĺ—ā–Ľ—Ź–≤–ĺ, –į –≤—ā–ĺ—Ä–ĺ—ā–ĺ –Ķ –ĺ—ā–Ľ—Ź–≤–ĺ, –ī–ĺ–ļ–į—ā–ĺ –≤ K –Ī–Ķ—ą–Ķ –ĺ—ā–ī—Ź—Ā–Ĺ–ĺ. –í —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ –Ľ—Ź–≤–ĺ –ł –ī—Ź—Ā–Ĺ–ĺ –∑–į–≤–ł—Ā—Ź—ā –ĺ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į –ł —Ā–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ł.
–ź–ļ–ĺ —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ 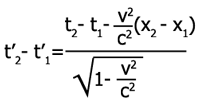 –Ņ—Ä–ł (t2 - t1) >0 –ł (x2 - x1 )>0 –ł–∑–≤–ĺ–ī–ł—ā–Ķ —Ā–į:
–Ņ—Ä–ł (t2 - t1) >0 –ł (x2 - x1 )>0 –ł–∑–≤–ĺ–ī–ł—ā–Ķ —Ā–į:
- –ź–ļ–ĺ (t2 - t1) > V2/c2(x2 - x1 ), —ā–ĺ –≤–ł–Ĺ–į–≥–ł (t'2 - t'1) >0, —ā–ĺ–Ķ—Ā—ā –ł –≤ K' –Ņ—ä—Ä–≤–ĺ—ā–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ —Ā–ł –ĺ—Ā—ā–į–≤–į –Ņ—ä—Ä–≤–ĺ
- –ź–ļ–ĺ (t2 - t1) = V2/c2(x2 - x1 ), —ā–ĺ–≥–į–≤–į (t'2 - t'1) =0 –ł–Ľ–ł –≤ K' –ī–≤–Ķ—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź —Ā—ā–į–≤–į—ā –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ. –ó–į –ī–į –Ķ –ł–∑–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ –ĺ–Ī–į—á–Ķ —ā—Ä—Ź–Ī–≤–į (x2 - x1)/(t2 - t1).V=c2 , –Ĺ–ĺ V<c, (x2 - x1)/(t2 - t1)>c , —ā.–Ķ. x2 - x1> c(t2 - t1). –Ę—ä–Ļ –ļ–į—ā–ĺ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į–ľ–Ķ –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł, –∑–į –ļ–ĺ–ł—ā–ĺ (x2 - x1)2 - c2(t2 - t1)2< 0 , —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ—ā–ĺ t'2 = t'1 –Ĺ–Ķ —Ā–Ķ –ł–∑–Ņ—ä–Ľ–Ĺ—Ź–≤–į.
- –ź–ļ–ĺ (t2 - t1) < V2/c2(x2 - x1 ), —ā–ĺ (t'2 - t'1) <0, —ā–ĺ–Ķ—Ā—ā –ł –≤ K' –Ņ—ä—Ä–≤–ĺ—ā–ĺ —Ā—ä–Ī–ł—ā–ł–Ķ –ĺ—Ā—ā–į–≤–į –≤—ā–ĺ—Ä–ĺ. –Ę–ĺ–≥–į–≤–į –ĺ–Ī–į—á–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ –ł–∑–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ (x2 - x1)/(t2 - t1)>c , –ļ–ĺ–Ķ—ā–ĺ –∑–į –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –Ĺ–Ķ –Ķ –≤ —Ā–ł–Ľ–į
–ö–į–ļ–≤–ĺ —Ā–Ľ–Ķ–ī–≤–į: –ü—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ķ–Ĺ–ł—ā–Ķ —Ā—ä–Ī–ł—ā–ł—Ź, —Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ł –ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ —Ā–ł –ĺ—Ā—ā–į–≤–į—ā –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ-—Ā–Ľ–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–ł –∑–į—Ź –≤—Ā—Ź–ļ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į - t2 > t1 —Ā–Ķ –∑–į–Ņ–į–∑–≤–į –≤–ł–Ĺ–į–≥–ł. –ě–Ī–į—á–Ķ (x2 - x1 )>0 –Ĺ–Ķ –≤–ł–Ĺ–į–≥–ł —Ā–Ķ –∑–į–Ņ–į–∑–≤–į –ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź—ā–į –Ľ—Ź–≤–ĺ –ł –ī—Ź—Ā–Ĺ–ĺ —Ā–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ł.
–ě—Ā–ĺ–Ī–Ķ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł. –†–į–≤–Ĺ–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł
–Ę—Ä—Ź–Ī–≤–į –ī–į –≤–ł –ĺ–Ī—ä—Ä–Ĺ–į –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, —á–Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į –Ĺ–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ-–≤—Ä–Ķ–ľ–Ķ—ā–ĺ –Ĺ–į –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł –Ĺ–Ķ –Ķ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–į. –ł –ľ–Ĺ–ĺ–≥–ĺ –Ĺ–į—ą–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł —ā—É–ļ –Ĺ–Ķ –≤–į–∂–į—ā.
–ē–ī–Ĺ–ĺ –ĺ—ā –Ĺ–Ķ—Č–į—ā–į, –ļ–ĺ–Ķ—ā–ĺ –Ņ—Ä–į–≤–ł –≤–Ņ–Ķ—á–į—ā–Ľ–Ķ–Ĺ–ł–Ķ –Ķ —Ą–į–ļ—ā—ä—ā, —á–Ķ –ļ–≤–į–ī—Ä–į—ā–į –Ĺ–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ļ–į–ļ—ā–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ–Ķ–Ĺ, —ā–į–ļ–į –ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ–Ķ–Ĺ. –í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā —ā–ĺ–≤–į, –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł—ā–Ķ —Ā–Ķ —Ä–į–∑–ī–Ķ–Ľ—Ź—ā –Ĺ–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į, –∑–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ł–ľ–į –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł, —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ī–ĺ –ļ–ĺ–ł—ā–ĺ –Ķ –Ĺ—É–Ľ–į. –ź–ļ–ĺ –≤–∑–Ķ–ľ–Ķ–ľ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ī–≤–Ķ —ā–ĺ—á–ļ–ł —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł (0, 0) –ł (1, 1) –ł –ł–∑—á–ł—Ā–Ľ–ł–ľ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É —ā—Ź—Ö, –Ņ–ĺ–Ľ—É—á–į–≤–į–ľ–Ķ 0.
|
–Ě–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –≤–ī—Ź—Ā–Ĺ–ĺ, –≤ –∑–Ķ–Ľ–Ķ–Ĺ–ĺ —Ā–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł, –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ - –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł, —á–Ķ—Ä–Ĺ–ł—Ź—ā –ī–ł–į–≥–ĺ–Ĺ–į–Ľ –Ņ–ĺ–ī 45 –≥—Ä–į–ī—É—Ā–į –Ķ –Ľ–ł–Ĺ–ł—Ź—ā–į –Ĺ–į "—Ā–≤–Ķ—ā–Ľ–ł–Ĺ–Ĺ–ł—Ź –ļ–ĺ–Ĺ—É—Ā". –Ę—ä–Ļ –ļ–į—ā–ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ—ä—ā —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź–≤–į –Ņ–ĺ –Ĺ–Ķ–ĺ–Ī–ł—á–į–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ, –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā —Ä–į–≤–Ĺ–ł –ĺ—ā—Ā–Ķ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī –Ĺ–Ķ —Ā–į —Ä–į–≤–Ĺ–ł. –Ě–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į, –∑–Ķ–Ľ–Ķ–Ĺ–ł—ā–Ķ –ĺ—ā—Ā–Ķ—á–ļ–ł —Ā–į —Ä–į–≤–Ĺ–ł –Ņ–ĺ–ľ–Ķ–∂–ī—É —Ā–ł: –∑–į "–ļ—ä—Ā–į—ā–į" S2=32-02=9, –∑–į "–ī—ä–Ľ–≥–į—ā–į" S2=52-42=9. –ß–Ķ—Ä–≤–Ķ–Ĺ–ł—ā–Ķ —Ā—ä—Č–ĺ —Ā–į —Ä–į–≤–Ĺ–ł –Ķ–ī–Ĺ–į –Ĺ–į –ī—Ä—É–≥–į –ł S2=-9. |
 –ė–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź: michurin.net –ė–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź: michurin.net |
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
–Ę–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –ź–Ļ–Ĺ—Č–į–Ļ–Ĺ, –Ē–ĺ—á–ĺ –ď. –§–į–ļ–ł—Ä–ĺ–≤, –°–ĺ—Ą–ł—Ź, 1961–≥, –Ē–ė "–Ě–į—Ä–ĺ–ī–Ĺ–į –Ņ—Ä–ĺ—Ā–≤–Ķ—ā–į"
–ß–Ķ—ā—č—Ä–Ķ—Ö–ľ–Ķ—Ä–Ĺ—č–Ļ –ľ–ł—Ä –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ĺ–≥–ĺ, –ď–Ķ—Ä–ľ–į–Ĺ –ź. –†–ĺ–∑–ľ–į–Ĺ
How do light cones limit time travel?
Vector product homes for the imaginary..., University of Missouri
–ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ł –≤—Ä–Ķ–ľ—Ź, –ď. –ú–ł–Ĺ–ļ–ĺ–≤—Ā–ļ–ł–Ļ
–†–Ķ–Ľ—Ź—ā–ł–≤–ł—Ā—ā—Ā–ļ–ł–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź –≤ –ļ—É—Ä—Ā–Ķ –ĺ–Ī—Č–Ķ–Ļ —Ą–ł–∑–ł–ļ–ł, –ē.–ė.–Ď—É—ā–ł–ļ–ĺ–≤
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–§–ł–∑–ł–ļ–į
–†–Ķ–Ľ–į—ā–ł–≤–ł—Ā—ā–ł—á–Ĺ–ĺ —É–≤–Ķ–Ľ–ł—á–į–≤–į–Ĺ–Ķ –Ĺ–į –ľ–į—Ā–į—ā–į. –ē–Ĺ–Ķ—Ä–≥–ł—Ź—ā–į: E = m.c2

–§–ł–∑–ł–ļ–į
–ē—Ą–Ķ–ļ—ā—ä—ā –∑–į–Ī–į–≤—Ź–Ĺ–Ķ –Ĺ–į –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –ł —Ā–ļ—ä—Ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į –ī—ä–Ľ–∂–ł–Ĺ–ł—ā–Ķ

–§–ł–∑–ł–ļ–į
–°–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–į—ā–į —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į



















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
4I4ATA
–Ě–ĺ–≤, —Ā–ļ—Ä–ł—ā –ī–ĺ—Ā–Ķ–≥–į –≤—Ö–ĺ–ī –≤ –Ņ–ł—Ä–į–ľ–ł–ī–į—ā–į –Ĺ–į –ú–ł–ļ–Ķ—Ä–ł–Ĺ –Ķ –ĺ—ā–ļ—Ä–ł—ā –Ņ–ĺ –į–Ĺ–ĺ–ľ–į–Ľ–ł–ł –Ņ—Ä–ł —Ā–ļ–į–Ĺ–ł—Ä–į–Ĺ–Ķ
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews