

–ź–ļ–ĺ —ā—ä—Ä—Ā–ł—ā–Ķ –ļ—ä–ī–Ķ –ī–į —Ā–ł –Ĺ–į–Ľ–Ķ–Ķ—ā–Ķ –Ņ–ł—ā–ł–Ķ, –Ķ–ī–Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ĺ—Ź–ľ–į –ī–į –≤–ł —Ā–≤—ä—Ä—ą–ł —Ä–į–Ī–ĺ—ā–į. –Ę—Ź –ľ–ĺ–∂–Ķ –ī–į –≤–ł –Ĺ–į–Ņ–ĺ–ľ–Ĺ—Ź –Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į, –Ĺ–ĺ –Ĺ—Ź–ľ–į –Ĺ–ł–ļ–į–ļ—ä–≤ –ĺ–Ī–Ķ–ľ, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ¬†–ļ–į–ļ–≤–ĺ—ā–ĺ –ł –ī–į —Ā–Ķ –Ĺ–į–Ľ–ł–≤–į "–≤—ä—ā—Ä–Ķ", —Č–Ķ —Ā–Ķ –ĺ–ļ–į–∂–Ķ –Ĺ–į–≤—ä–Ĺ.
–ö–į–ļ –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł —ā–į–ļ–ĺ–≤–į —Ā—ā—Ä–į–Ĺ–Ĺ–ĺ –Ĺ–Ķ—Č–ĺ –ł –∑–į—Č–ĺ –Ĺ–ł —ā—Ä—Ź–Ī–≤–į?
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –§–Ķ–Ľ–ł–ļ—Ā –ö–Ľ–į–Ļ–Ĺ , –ļ–ĺ–Ļ—ā–ĺ –Ķ –ĺ—ā–ļ—Ä–ł–Ľ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ņ—Ä–Ķ–∑ 1882 –≥., —Ź –ĺ–Ņ–ł—Ā–≤–į –ļ–į—ā–ĺ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā, –ļ–ĺ—Ź—ā–ĺ "–ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –≤–ł–∑—É–į–Ľ–ł–∑–ł—Ä–į –ļ–į—ā–ĺ —Ā–Ķ –ĺ–Ī—ä—Ä–Ĺ–Ķ –Ņ–į—Ä—á–Ķ –≥—É–ľ–Ķ–Ĺ–į —ā—Ä—ä–Ī–į –ł –ī–į –Ĺ–į–Ņ—Ä–į–≤–ł–ľ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į –Ņ—Ä–Ķ–ľ–ł–Ĺ–Ķ –Ņ—Ä–Ķ–∑ —Ā–Ķ–Ī–Ķ —Ā–ł, —ā–į–ļ–į —á–Ķ –≤—ä—ā—Ä–Ķ—ą–Ĺ–į—ā–į –ł –≤—ä–Ĺ—ą–Ĺ–į—ā–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –ī–į —Ā–Ķ —Ā—Ä–Ķ—Č–Ĺ–į—ā".¬†–Ď—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ķ –≤ –≥–į–Ľ–Ķ—Ä–ł—Ź—ā–į –Ĺ–į –Ĺ–į–Ļ-–Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —Ą–ĺ—Ä–ľ–ł, –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł –Ĺ–į —ą–ł—Ä–ĺ–ļ–į—ā–į –Ņ—É–Ī–Ľ–ł–ļ–į.¬†
–Ď—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į¬†–ö–Ľ–į–Ļ–Ĺ —Ā–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į –ļ–į—ā–ĺ —Ā–Ķ —Ā—ä–Ķ–ī–ł–Ĺ—Ź—ā –ī–≤–Ķ—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –Ľ–ł—Ā—ā, –∑–į –ī–į —Ā—ā–į–Ĺ–Ķ —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä (—ā—Ä—ä–Ī–į), –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–Ķ –ł–∑–≤–ł–≤–į—ā –ļ—Ä–į–ł—Č–į—ā–į –Ĺ–į —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä–į –ĺ–Ī—Ä–į—ā–Ĺ–ĺ –Ņ—Ä–Ķ–∑ —Ā–į–ľ–ł—Ź –Ĺ–Ķ–≥–ĺ –Ņ–ĺ —ā–į–ļ—ä–≤ –Ĺ–į—á–ł–Ĺ, —á–Ķ –≤—ä—ā—Ä–Ķ—ą–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į (–≤ –∑–Ķ–Ľ–Ķ–Ĺ–ĺ) –ł –≤—ä–Ĺ—ą–Ĺ–į—ā–į (–≤ –Ī—Ź–Ľ–ĺ) –Ĺ–į —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä–į —Ā–Ķ —Ā—ä–Ķ–ī–ł–Ĺ—Ź–≤–į—ā. –ź–Ĺ–ł–ľ–į—Ü–ł—Ź –ĺ—ā Konrad Polthier.
–ě—á–Ķ–≤–ł–ī–Ĺ–ĺ –Ķ, —á–Ķ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ, —ā–ĺ—á–Ĺ–ĺ –ļ–į—ā–ĺ –Ņ–ĺ-–Ņ–ĺ–∑–Ĺ–į—ā–į—ā–į –Ĺ–ł —Ā—Ą–Ķ—Ä–į, –Ķ –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā: —ā—Ź –Ķ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–į, –≤ —Ā–ľ–ł—Ā—ä–Ľ, —á–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –≤–ľ–Ķ—Ā—ā–ł –≤ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā –Ĺ–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ. –ē–ī–Ĺ–į –ľ—Ä–į–≤–ļ–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ä–į–∑—Ö–ĺ–∂–ī–į –Ņ–ĺ –Ĺ–Ķ—Ź –≤–Ķ—á–Ĺ–ĺ, –Ī–Ķ–∑ –ł–∑–ĺ–Ī—Č–ĺ –ī–į —Ā–Ķ –Ĺ–į—ā—ä–ļ–Ĺ–Ķ –Ĺ–į –≥—Ä–į–Ĺ–ł—Ü–į –ł–Ľ–ł –ī–į –Ņ–į–ī–Ĺ–Ķ –ĺ—ā –Ĺ—Ź–ļ–ĺ–Ļ¬†—Ä—ä–Ī. –ó–į —Ä–į–∑–Ľ–ł–ļ–į –ĺ—ā —Ā—Ą–Ķ—Ä–į—ā–į, –ļ–ĺ—Ź—ā–ĺ –ł–ľ–į –≤—ä—ā—Ä–Ķ—ą–Ĺ–į –ł –≤—ä–Ĺ—ą–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā, –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –ĺ–Ī–į—á–Ķ –ł–ľ–į¬†–Ķ–ī–Ĺ–į —Ā—ā—Ä–į–Ĺ–į: —Ä–į–∑—Ö–ĺ–∂–ī–į–Ļ–ļ–ł —Ā–Ķ –Ĺ–į—ą–į—ā–į –ľ—Ä–į–≤–ļ–į –ľ–ĺ–∂–Ķ –ī–į –ī–ĺ—Ā—ā–ł–≥–Ĺ–Ķ –ī–ĺ –ī–≤–Ķ—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ĺ—ā –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į.
–Ď—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–Ķ –ĺ–Ī—Ö–≤–į—Č–į –ĺ–Ī–Ķ–ľ –ł –Ĺ–ł—Č–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–Ľ–Ķ–Ķ–ľ "–≤—ä—ā—Ä–Ķ", –∑–į—Č–ĺ—ā–ĺ –Ĺ—Ź–ľ–į "–≤—ä—ā—Ä–Ķ" –ł–Ľ–ł "–≤—ä–Ĺ" - –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į –Ķ –Ķ–ī–Ĺ–į.
–ź —ā–ĺ–≤–į –Ņ—Ä–į–≤–ł –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–į, –∑–į—Č–ĺ—ā–ĺ –Ĺ–Ķ —Ā–Ķ —Ā—Ä–Ķ—Č–į—ā¬†—á–Ķ—Ā—ā–ĺ –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ł —Ą–ĺ—Ä–ľ–ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į.¬†
–ú—Ć–ĺ–Ī–ł—É—Ā–ĺ–≤–į—ā–į –Ľ–Ķ–Ĺ—ā–į –Ķ –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–į. –°—Ö–Ķ–ľ–į –ł –į–Ĺ–ł–ľ–į—Ü–ł—Ź: Konrad Polthier.¬†
–ź–ļ–ĺ –Ī—É—ā–ł–Ľ–ļ–į—ā–į¬†–Ķ –ľ–į–Ľ–ļ–ĺ –ĺ–Ī—ä—Ä–ļ–≤–į—Č–į, –ł–ľ–į –Ķ–ī–ł–Ĺ –Ņ–ĺ-–Ņ—Ä–ĺ—Ā—ā –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā: –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—Ź—ā –ú—Ć–ĺ–Ī–ł—É—Ā–ĺ–≤ –Ľ–ł—Ā—ā. –ú–ĺ–∂–Ķ—ā–Ķ –ī–į –Ĺ–į–Ņ—Ä–į–≤–ł—ā–Ķ –Ķ–ī–ł–Ĺ, –ļ–į—ā–ĺ –ĺ–Ī—ä—Ä–Ĺ–Ķ—ā–Ķ –Ķ–ī–ł–Ĺ –ĺ—ā¬†–ī–≤–į—ā–į –ļ—Ä–į—Ź –Ĺ–į –Ľ–Ķ–Ĺ—ā–į –ĺ—ā —Ö–į—Ä—ā–ł—Ź –ł –≥–ĺ –∑–į–Ľ–Ķ–Ņ–ł—ā–Ķ –Ĺ–į –ī—Ä—É–≥–ł—Ź –ļ—Ä–į–Ļ. –° –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į —Ö–į—Ä—ā–ł–Ķ–Ĺ–į –Ľ–Ķ–Ĺ—ā–į, —á–ł–ł—ā–ĺ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –ł–ľ–į—ā —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ, –ī–į –ļ–į–∂–Ķ–ľ, –∑–Ķ–Ľ–Ķ–Ĺ–ĺ –ł –ĺ—Ä–į–Ĺ–∂–Ķ–≤–ĺ, –Ľ–Ķ—Ā–Ĺ–ĺ —Č–Ķ —Ā–Ķ —É–Ī–Ķ–ī–ł—ā–Ķ, —á–Ķ –ú—Ć–ĺ–Ī–ł—É—Ā–ĺ–≤–į—ā–į –Ľ–Ķ–Ĺ—ā–į –Ķ –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–į. –°–Ľ–Ķ–ī –ļ–į—ā–ĺ —Ā—ā–Ķ —É—Ā—É–ļ–į–Ľ–ł –ļ—Ä–į–ł—Č–į—ā–į –ł –∑–į–Ľ–Ķ–Ņ–ł–Ľ–ł, —Č–Ķ –ĺ—ā–ļ—Ä–ł–Ķ—ā–Ķ, —á–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā—ā–ł–≥–Ĺ–Ķ—ā–Ķ –ī–ĺ –≤—Ā—Ź–ļ–į –ĺ—Ä–į–Ĺ–∂–Ķ–≤–į –ł¬†–≤—Ā—Ź–ļ–į –∑–Ķ–Ľ–Ķ–Ĺ–į —ā–ĺ—á–ļ–į, –Ī–Ķ–∑ –ī–į —Ā–Ķ –Ĺ–į–Ľ–į–≥–į –ī–į –Ņ—Ä–ĺ–Ī–ł–≤–į—ā–Ķ —Ö–į—Ä—ā–ł—Ź—ā–į –ł–Ľ–ł –ī–į —Ā–Ķ –ļ–į—ā–Ķ—Ä–ł—ā–Ķ –Ņ—Ä–Ķ–∑ —Ä—ä–Ī–į –Ļ.
–ó–į —Ä–į–∑–Ľ–ł–ļ–į –ĺ—ā –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į¬†–ö–Ľ–į–Ļ–Ĺ, –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā –ł–ľ–į –ļ—Ä–į–Ļ, –ł–ľ–į –≥—Ä–į–Ĺ–ł—Ü–į - —ā—Ź —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –ī–≤–į—ā–į –ĺ—ā–ī–Ķ–Ľ–Ĺ–ł —Ā–Ľ–Ķ–Ņ–Ķ–Ĺ–ł –ļ—Ä–į–ł—Č–į –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–į—ā–į –Ľ–Ķ–Ĺ—ā–į. –Ě–ĺ –ī–≤–į—ā–į –ļ—Ä–į—Ź —Ā–į —Ā–≤—ä—Ä–∑–į–Ĺ–ł.¬†–ď—Ä–į–Ĺ–ł—Ü–į—ā–į –Ĺ–į –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā –Ķ –Ķ–ī–ł–Ĺ–ł—á–Ĺ–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į –ļ—Ä–ł–≤–į.
–ź–ļ–ĺ –ł–ľ–į–ľ–Ķ –ī–≤–Ķ –ú—Ć–ĺ–Ī–ł—É—Ā–ĺ–≤–ł –Ľ–Ķ–Ĺ—ā–ł –∑–į –ī–į —Ā–Ķ —Ā—ä–∑–ī–į–ī–Ķ –Ķ–ī–Ĺ–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į —Ą–ĺ—Ä–ľ–į, –ļ–į—ā–ĺ —Ā–Ķ –Ņ—Ä–ł—Ā—ä–Ķ–ī–ł–Ĺ—Ź—ā —ā–Ķ—Ö–Ĺ–ł—ā–Ķ –≥—Ä–į–Ĺ–ł—Ü–ł —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–į –ī–≤—É—Ā—ā—Ä–į–Ĺ–Ĺ–į –Ľ–Ķ–Ĺ—ā–į, –ļ–į–ļ—ā–ĺ –Ķ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ņ–ĺ-–ī–ĺ–Ľ—É, –į —ā–ĺ–≤–į, –ļ–ĺ–Ķ—ā–ĺ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į –Ķ —ā–ĺ—á–Ĺ–ĺ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ.
–Ē—Ä—É–≥–į –Ľ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ—Ā—ā –Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ķ, —á–Ķ —Ā–į–ľ–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ķ —ā—Ä—É–ī–Ĺ–ĺ –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł –ĺ—ā –Ķ–ī–Ĺ–į –ļ–į—É—á—É–ļ–ĺ–≤–į —ā—Ä—ä–Ī–į –ļ–į–ļ—ā–ĺ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į –ö–Ľ–į–Ļ–Ĺ. –°—ā—Ä–ĺ–≥–ĺ –Ņ–ĺ–≥–Ľ–Ķ–ī–Ĺ–į—ā–ĺ, —Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į—Č–ł—ā–Ķ —Ā–Ķ –ĺ–Ī–Ķ–ļ—ā–ł –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł –Ņ–ĺ-–≥–ĺ—Ä–Ķ, –Ĺ–Ķ —Ā–į –Ī—É—ā–ł–Ľ–ļ–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ, –Ĺ–ĺ –ļ–į–ļ—ā–ĺ –Ņ–ĺ—Ā–ĺ—á–≤–į –ö–Ľ–į–Ļ–Ĺ, —ā—Ź –Ķ —Ā–į–ľ–ĺ –≤—ä–ĺ–Ī—Ä–į–∂–į–Ķ–ľ –ĺ–Ī–Ķ–ļ—ā –≤ –Ĺ–į—ą–Ķ—ā–ĺ 3D –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ.¬†¬†–Ě–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ —É—Ā–Ņ–Ķ—ą–Ĺ–ĺ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ł—Ä–į–Ĺ–į –≤ 4D¬†–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ,¬†–Ī–Ķ–∑¬†—Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ –ł –ī—É–Ņ–ļ–į –≤ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ł–Ĺ–į—ā–į.
–ó–į –ī–į —Ä–į–∑–Ī–Ķ—Ä–Ķ–ľ –∑–į—Č–ĺ, –Ņ—ä—Ä–≤–ĺ –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ī–ĺ–Ī—Ä–Ķ –Ņ–ĺ–∑–Ĺ–į—ā–ł—Ź –≥–Ķ–≤—Ä–Ķ–ļ –ł–Ľ–ł –Ņ–ĺ—Ź—Ā (–ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –ļ–į—ā–ĺ —ā–ĺ—Ä). –ú–ĺ–∂–Ķ –ī–į –Ĺ–į–Ņ—Ä–į–≤–ł–ľ —ā–ĺ—Ä –ĺ—ā –ļ–≤–į–ī—Ä–į—ā–Ķ–Ĺ –Ľ–ł—Ā—ā –ĺ—ā –ļ–į—É—á—É–ļ, –ļ–į—ā–ĺ –Ņ—ä—Ä–≤–ĺ –∑–į–Ľ–Ķ–Ņ–ł–ľ –ī–≤–Ķ—ā–Ķ —Ā—Ä–Ķ—Č—É–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä–į–Ĺ–ł –ļ–į—ā–ĺ —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä, –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –∑–į–Ľ–Ķ–Ņ–≤–į–ľ–Ķ –ī–≤–į—ā–į –ļ—Ä–į—Ź –Ĺ–į —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä–į –∑–į –ī–į –Ņ–ĺ–Ľ—É—á–ł–ľ —ā–ĺ—Ä.

–ü–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ –Ĺ–į —ā–ĺ—Ä: –ü—ä—Ä–≤–ĺ –∑–į–Ľ–Ķ–Ņ–≤–į–ľ–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –ī–≤–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į, –∑–į –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä –ł —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –∑–į–Ľ–Ķ–Ņ–Ķ—ā–Ķ –ī–≤–į—ā–į –≥—Ä–į–Ĺ–ł—á–Ĺ–ł –ļ—Ä—ä–≥–į –Ĺ–į —Ü–ł–Ľ–ł–Ĺ–ī—ä—Ä–į —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—Č–ł –Ĺ–į –∑–į–Ľ–Ķ–Ņ–≤–į–Ĺ–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —ā–ĺ—á–ļ–ł –Ĺ–į –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į –∑–į –ī–į –ĺ–Ī—Ä–į–∑—É–≤–į–ľ–Ķ —ā–ĺ—Ä.
–ź–ļ–ĺ –Ĺ–Ķ –ł—Ā–ļ–į—ā–Ķ –ī–į —Ā–Ķ –∑–į–Ĺ–ł–ľ–į–≤–į—ā–Ķ —Ā –Ľ–Ķ–Ņ–Ķ–Ĺ–Ķ, –ľ–ĺ–∂–Ķ—ā–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ –ī–į —Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā–Ķ¬†—ā–ĺ—Ä–į –ļ–į—ā–ĺ –ļ–≤–į–ī—Ä–į—ā –ļ–į—ā–ĺ –ł–ľ–į—ā–Ķ –Ņ—Ä–Ķ–ī–≤–ł–ī, —á–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł —Ā–Ķ —Ā–ľ—Ź—ā–į—ā –∑–į –Ķ–ī–Ĺ–ł –ł —Ā—ä—Č–ł. –Ę–į–ļ–į —á–Ķ, –ļ–ĺ–≥–į—ā–ĺ —Ā–Ķ –Ņ–Ľ—ä–∑–≥–į –Ĺ—Ź–ļ–į–ļ–≤–į —Ą–ł–≥—É—Ä–į, –Ĺ–į—Ä–ł—Ā—É–≤–į–Ĺ–į –≤—ä—Ä—Ö—É "–ļ–≤–į–ī—Ä–į—ā–į",¬†–ļ—ä–ľ –≥–ĺ—Ä–Ĺ–ł—Ź —Ä—ä–Ī, —ā—Ź —Č–Ķ —Ā–Ķ –Ņ–ĺ—Ź–≤–ł –ĺ—ā–Ĺ–ĺ–≤–ĺ –≤ –ī–ĺ–Ľ–Ĺ–ł—Ź –ļ—Ä–į–Ļ, –į –ļ–ĺ–≥–į—ā–ĺ —Ź –Ņ–Ľ—ä–∑–Ĺ–Ķ—ā–Ķ –ļ—ä–ľ –ī–Ķ—Ā–Ĺ–ł—Ź –ļ—Ä–į–Ļ —Č–Ķ —Ā–Ķ –Ņ–ĺ—Ź–≤–ł –ĺ—ā–Ĺ–ĺ–≤–ĺ –≤ –Ľ–Ķ–≤–ł—Ź —Ä—ä–Ī –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ.
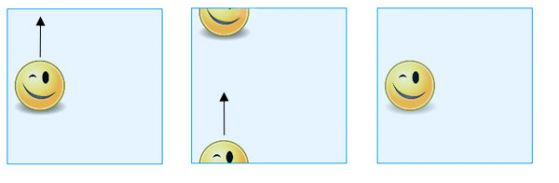
–ö–ĺ–≥–į—ā–ĺ –Ņ–Ľ—ä–∑–Ĺ–Ķ—ā–Ķ —Ą–ł–≥—É—Ä–į –Ĺ–į—Ä–ł—Ā—É–≤–į–Ĺ–į –≤—ä—Ä—Ö—É "–ļ–≤–į–ī—Ä–į—ā–į" –ļ—ä–ľ –≥–ĺ—Ä–Ĺ–ł—Ź —Ä—ä–Ī, —ā—Ź —Č–Ķ —Ā–Ķ –Ņ–ĺ—Ź–≤–ł –ĺ—ā–Ĺ–ĺ–≤–ĺ –≤ –ī–ĺ–Ľ–Ĺ–ł—Ź –ļ—Ä–į–Ļ.
–ó–į –ī–į –Ņ–ĺ–Ľ—É—á–ł—ā–Ķ –ł—Ā—ā–ł–Ĺ—Ā–ļ–į –Ī—É—ā–ł–Ľ–ļ–į –Ĺ–į¬†–ö–Ľ–į–Ļ–Ĺ, –∑–į–Ņ–ĺ—á–Ĺ–Ķ—ā–Ķ –Ņ–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ĺ –ļ–į—ā–ĺ –Ĺ–į–ľ–Ķ—Ä–ł—ā–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –ī–≤–ĺ–Ļ–ļ–į—ā–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į. –ó–į –ī—Ä—É–≥–į—ā–į –ī–≤–ĺ–Ļ–ļ–į —Ā—ā—Ä–į–Ĺ–ł, –ĺ–Ī–į—á–Ķ, –Ĺ–Ķ —Ā–Ķ –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł—Ü–ł—Ä–į—ā —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ—Ä—Ź–ļ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł, –į —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ, –ļ–į–ļ—ā–ĺ –Ķ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ā–Ĺ–ł–ľ–ļ–į—ā–į.
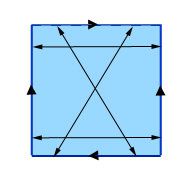
–ü–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ –Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ: —Ā—ä–Ķ–ī–ł–Ĺ—Ź–≤–≤–į—ā —Ā–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –ī–≤–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä–į–Ĺ–ł (–≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ–ł—ā–Ķ –≤ —ā–į–∑–ł —Ā—Ö–Ķ–ľ–į), –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–Ķ —Ā—ä–Ķ–ī–ł–Ĺ—Ź–≤–≤–į—ā ¬†–ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ –ī–≤–Ķ —Ā—ā—Ä–į–Ĺ–ł.¬†–ź–ļ–嬆–ļ–≤–į–ī—Ä–į—ā—ā—ä—ā –Ķ [0,1] √ó [0,1] –ĺ—ā—ä–∂–ī–Ķ—Ā—ā–≤—Ź–≤–į–ľ–Ķ —ā–ĺ—á–ļ–ł—ā–Ķ (x, -1) —Ā (-x, 1) –ł (-1, y) —Ā (1, y) . –Ę–į–ļ–į –ĺ—ā—ä–∂–ī–Ķ—Ā—ā–≤—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā—ā—Ä–į–Ĺ–ł—ā–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į –Ņ–ĺ x —Ā—ā–į–≤–į ‚Äě—Ā —É—Ā—É–ļ–≤–į–Ĺ–Ķ‚Äú, –į –Ņ–ĺ y - ‚Äě–Ī–Ķ–∑ —É—Ā—É–ļ–≤–į–Ĺ–Ķ‚Äú.
–ü–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź—ā –ĺ–Ī–Ķ–ļ—ā –Ķ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –ö–Ľ–į–Ļ–Ĺ. –ě—ā–Ĺ–ĺ–≤–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–ł —Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā–Ķ –ļ–į—ā–ĺ –ļ–≤–į–ī—Ä–į—ā –ļ–į—ā–ĺ –ł–ľ–į—ā–Ķ –Ņ—Ä–Ķ–ī–≤–ł–ī –ļ–ĺ–ł –≥—Ä–į–Ĺ–ł—á–Ĺ–ł —ā–ĺ—á–ļ–ł —Ā–Ķ —Ā–ľ—Ź—ā–į—ā –∑–į –Ķ–ī–Ĺ–ł –ł —Ā—ä—Č–ł. –ź–ļ–ĺ –Ņ–Ľ—ä–∑–Ĺ–Ķ—ā–Ķ —Ą–ł–≥—É—Ä–į—ā–į –Ĺ–į–ī –Ķ–ī–ł–Ĺ –ĺ—ā —Ä—ä–Ī–ĺ–≤–Ķ—ā–Ķ, –ļ–ĺ–ł—ā–ĺ –ł–ľ–į—ā –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ł —ā–ĺ—á–ļ–ł (–≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ–ł—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł –≤ –Ĺ–į—ą–ł—Ź —Ā–Ľ—É—á–į–Ļ), —ā—Ź —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –ĺ—ā–Ĺ–ĺ–≤–ĺ –Ĺ–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į, –ļ–į—ā–ĺ –Ņ—Ä–Ķ–ī–ł. –ź–ļ–ĺ –ĺ–Ī–į—á–Ķ —Ź –Ņ–Ľ—ä–∑–Ĺ–Ķ—ā–Ķ –Ĺ–į–ī –Ķ–ī–ł–Ĺ –ĺ—ā —Ä—ä–Ī–ĺ–≤–Ķ—ā–Ķ, —á–ł–ł—ā–ĺ —ā–ĺ—á–ļ–ł —Ā–į –Ī–ł–Ľ–ł –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł—Ü–ł—Ä–į–Ĺ–ł –Ņ–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ (—Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–ł—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł), —ā—Ź —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –Ĺ–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į, –Ĺ–ĺ –ł–∑–ľ–Ķ—Ā—ā–Ķ–Ĺ–į –ł –ļ–į—ā–ĺ –ĺ–≥–Ľ–Ķ–ī–į–Ľ–Ķ–Ĺ –ĺ–Ī—Ä–į–∑ –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ł—Ź —Ā–ł.
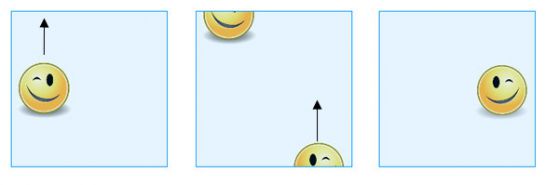
–ź–ļ–ĺ –Ņ–Ľ—ä–∑–Ĺ–Ķ—ā–Ķ —Ą–ĺ—Ä–ľ–į –Ĺ–į–ī –≥–ĺ—Ä–Ĺ–ł—Ź –ļ—Ä–į–Ļ, —ā—Ź —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –Ņ—Ä–Ķ–∑ –ī–ĺ–Ľ–Ĺ–ł—Ź —Ä—ä–Ī¬†–ĺ—ā¬†–ī—Ä—É–≥–į—ā–į —Ā—ā—Ä–į–Ĺ–į –ł –ļ–į—ā–ĺ –ĺ–≥–Ľ–Ķ–ī–į–Ľ–Ķ–Ĺ –ĺ–Ī—Ä–į–∑ –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ł—Ź —Ā–ł.
–ē–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–ł—Ź—ā –Ĺ–į—á–ł–Ĺ –ī–į —Ā–Ķ –ł–∑–≥—Ä–į–ī–ł —ā–į–∑–ł —Ą–ĺ—Ä–ľ–į –≤ —ā—Ä–ł–ł–∑–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ķ –ī–į —Ā–Ķ –ī–į–ī–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā —ā—Ź –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į. –Ę–ĺ–≤–į —Ā–Ķ —Ä–į–≤–Ĺ—Ź–≤–į –Ĺ–į –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł—Ü–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–≤–ĺ–Ļ–ļ–ł –ĺ—ā —ā–ĺ—á–ļ–ł –≤—ä–≤ –≤—ä—ā—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ł—Ź –ļ–≤–į–ī—Ä–į—ā, —ā–į–ļ–į —á–Ķ —Ā—ā—Ä–ĺ–≥–ĺ –Ņ–ĺ–≥–Ľ–Ķ–ī–Ĺ–į—ā–ĺ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į—ā–į —Ą–ł–≥—É—Ä–į –Ĺ–Ķ –Ķ —ā–ĺ—á–Ĺ–ĺ —Ā—ä—Č–į—ā–į –ļ–į—ā–ĺ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ–ł. –Ę–ĺ–≤–į –Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ –Ķ–ī–ł–Ĺ –Ĺ–į—á–ł–Ĺ –∑–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ –Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į—ā–į –≤ —ā—Ä–ł–ł–∑–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ (–ł–ľ–į –ł –ī—Ä—É–≥–ł).
–ě—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–ĺ—Ā—ā –ł –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ĺ—Ā—ā
–Ě–į–Ļ-–≤–į–∂–Ĺ–ł—ā–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ĺ–į –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā –ł –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ —Ā–į —ā—Ź—Ö–Ĺ–į—ā–į –ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–ĺ—Ā—ā –ł –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ĺ—Ā—ā. –ē–ī–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā –Ķ –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–į, –į–ļ–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ä–į–∑—Ö–ĺ–ī–ł—ā–Ķ –Ņ—Ä–į–≤ –Ņ–ĺ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į –ļ–į—ā–ĺ —Ā—ā–ł–≥–Ĺ–Ķ—ā–Ķ –ī–ĺ –ī–≤–Ķ—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ĺ—ā –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į. –ü–ĺ–≤–Ķ—á–Ķ—ā–ĺ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į —Ā–į –ī–≤—É—Ā—ā—Ä–į–Ĺ–Ĺ–ł . –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ļ—Ä—ä–≥–Ľ–į —Ā—Ą–Ķ—Ä–į –Ķ –ī–≤—É—Ā—ā—Ä–į–Ĺ–Ĺ–į, –ļ–ĺ–Ķ—ā–ĺ –Ķ –≥–į—Ä–į–Ĺ—Ü–ł—Ź, —á–Ķ –≤–ł–Ĺ–į–≥–ł —Č–Ķ —Ö–ĺ–ī–ł–ľ –≤—ä—Ä—Ö—É –ó–Ķ–ľ—Ź—ā–į –ł –Ĺ–ł–ļ–ĺ–≥–į —Ā –≥–Ľ–į–≤–į –≤ —Ā–ļ–į–Ľ–ł—ā–Ķ. –ü–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ĺ –ł –Ņ–ĺ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į —ā–ĺ—Ä–į (–≥–Ķ–≤—Ä–Ķ–ļ–į) –ł –≤—ä–ĺ–Ī—Č–Ķ –Ņ–ĺ –≤—Ā–ł—á–ļ–ł –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā–ł, –ļ–ĺ–ł—ā–ĺ –Ņ–ĺ–ļ—Ä–ł–≤–į—ā —ā–≤—ä—Ä–ī –ĺ–Ī–Ķ–ľ, —Ā–į –ī–≤—É—Ā—ā—Ä–į–Ĺ–Ĺ–ł.
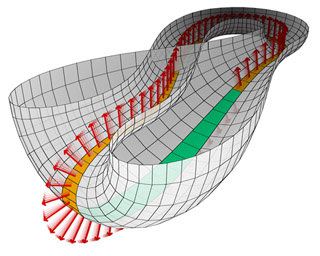
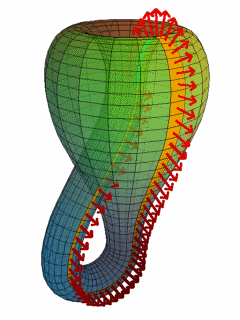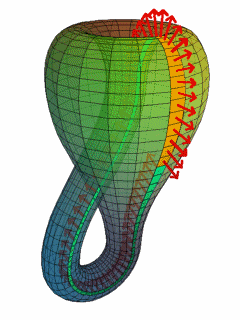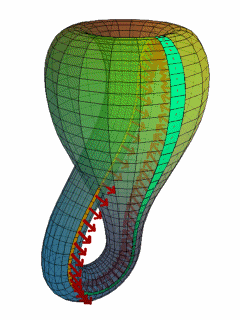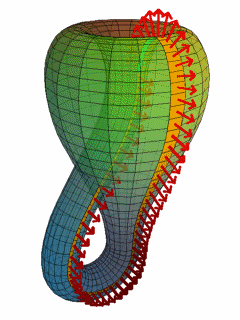
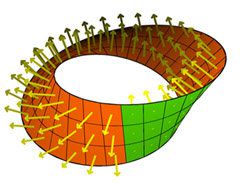
–í –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –≤–ł–ī—Ź—ā –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ł –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ł–Ĺ–ł. –ü—ä—Ä–≤–į—ā–į –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā, –ĺ—ā–ļ—Ä–ł—ā–į –ĺ—ā –ú—Ć–ĺ–Ī–ł—É—Ā, –Ķ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ. –ü–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ł—ā–Ķ —Ā—ā—Ä–Ķ–Ľ–ł—á–ļ–ł (–Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł - –Ĺ–ĺ—Ä–ľ–į–Ľ–Ĺ–ł –≤–Ķ–ļ—ā–ĺ—Ä–ł ), –ļ–ĺ–ł—ā–ĺ –≤–ł–ī—Ź—Ö–ľ–Ķ –Ņ–ĺ-–≥–ĺ—Ä–Ķ –≤—ä—Ä—Ö—É –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā, –≤ –≥–ĺ—Ä–Ĺ–į—ā–į –ł–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź –Ĺ–į –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ņ–ĺ–ļ–į–∑–≤–į—ā –Ĺ–Ķ–Ļ–Ĺ–į—ā–į –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ĺ—Ā—ā: ¬†–Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–ĺ –ī–≤–ł–∂–Ķ–Ļ–ļ–ł —Ā–Ķ, —Ā—ā—Ä–Ķ–Ľ–ł—á–ļ–ł—ā–Ķ –ĺ–Ī—Ö–ĺ–∂–ī–į—ā –ī–≤–Ķ—ā–Ķ —Ā—ā—Ä–į–Ĺ–ł –Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ĺ—Ź–ľ–į —Ä–į–∑–Ľ–ł–ļ–į –ľ–Ķ–∂–ī—É –≥–ĺ—Ä–Ĺ–ĺ –ł –ī–ĺ–Ľ–Ĺ–ĺ (–Ņ—Ä–Ķ–ī–Ĺ–ĺ –ł –∑–į–ī–Ĺ–ĺ, –≤—ä—ā—Ä–Ķ –ł –≤—ä–Ĺ).
–õ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–ĺ—ā–ĺ –Ķ, —á–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź—ā–į –∑–į "–≤—ä—ā—Ä–Ķ", "–ĺ—ā–≤—ä–Ĺ" –ł "–Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ—á–ł–≤–ĺ—Ā—ā" –∑–į–≤–ł—Ā—Ź—ā –ĺ—ā –ĺ–ļ–ĺ–Ľ–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –≤ –ļ–ĺ–Ķ—ā–ĺ –ĺ–Ī–Ķ–ļ—ā—ä—ā —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ–ī–Ĺ–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į –ļ—Ä–ł–≤–į (–ļ–ĺ–Ĺ—ā—É—Ä), –Ĺ–į—Ä–ł—Ā—É–≤–į–Ĺ–į –≤—ä—Ä—Ö—É –Ľ–ł—Ā—ā —Ö–į—Ä—ā–ł—Ź (—ā.–Ķ. –≤ –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ) –ł–ľ–į –ī–ĺ–Ī—Ä–Ķ –ī–Ķ—Ą–ł–Ĺ–ł—Ä–į–Ĺ–ł "–≤—ä—ā—Ä–Ķ" –ł "–ĺ—ā–≤—ä–Ĺ", —ā–ĺ –Ņ—Ä–ł —Ā—ä—Č–ł—Ź—ā¬†–ļ–ĺ–Ĺ—ā—É—Ä, –Ņ–ĺ—Ā—ā–į–≤–Ķ–Ĺ –≤ —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, —ā–Ķ–∑–ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –≥—É–Ī—Ź—ā —Ā–ľ–ł—Ā—ä–Ľ. –ē—ā–ĺ –∑–į—Č–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –≥–ĺ–≤–ĺ—Ä–ł–ľ –∑–į –Ķ–ī–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ—á–ł–≤–ĺ—Ā—ā, –ĺ—Ā–≤–Ķ–Ĺ –į–ļ–ĺ –Ņ—ä—Ä–≤–ĺ –Ĺ–Ķ —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł¬†–ļ–į–ļ —Ā–Ķ –≤–≥—Ä–į–∂–ī–į —ā–į–∑–ł –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ł–Ĺ–į –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ. –ė–ľ–į –ĺ–Ī–į—á–Ķ –Ņ–ĺ-—ā—Ź—Ā–Ĺ–ĺ —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į, –Ņ—Ä–ł—Ā—ä—Č–ł –Ĺ–į –Ķ–ī–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ł–Ĺ–į—ā–į, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ –∑–į–≤–ł—Ā—Ź—ā –ĺ—ā –ĺ–ļ–ĺ–Ľ–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ.
–ó–į –Ķ–ī–Ĺ–į¬†–Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā —Ā–Ķ –ļ–į–∑–≤–į, —á–Ķ –Ķ –ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–į, –į–ļ–ĺ —Ą–ł–≥—É—Ä–į, –Ĺ–į—Ä–ł—Ā—É–≤–į–Ĺ–į –≤—ä—Ä—Ö—É –Ĺ–Ķ—Ź, –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–ł—Ä–į –≤ —Ā–≤–ĺ—Ź –ĺ–≥–Ľ–Ķ–ī–į–Ľ–Ķ–Ĺ –ĺ–Ī—Ä–į–∑, –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –ł –ī–į —Ā–Ķ –Ņ–Ľ—ä–∑–≥–į –Ņ–ĺ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į.
–ě—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–ĺ—Ā—ā. –ź–Ĺ–ł–ľ–į—Ü–ł—Ź –ĺ—ā Konrad Polthier
–ö–į–ļ—ā–ĺ –ľ–ĺ–∂–Ķ—ā–Ķ –ī–į –≤–ł–ī–ł—ā–Ķ –≤ –į–Ĺ–ł–ľ–į—Ü–ł—Ź—ā–į –≥–ĺ—Ä–Ķ,¬†–į–ļ–ĺ –Ņ—Ä–ł–ī–≤–ł–∂–ł—ā–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ľ–ł—Ü–Ķ –ĺ–ļ–ĺ–Ľ–ĺ –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā, —ā–ĺ —Ā–Ķ –∑–į–≤—Ä—ä—Č–į –ļ–į—ā–ĺ —Ā–≤–ĺ—Ź –ĺ–≥–Ľ–Ķ–ī–į–Ľ–Ķ–Ĺ –ĺ–Ī—Ä–į–∑ ( —Ā –≥–Ľ–į–≤–į—ā–į –Ĺ–į–ī–ĺ–Ľ—É). –Ę–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ľ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į¬†–ú—Ć–ĺ–Ī–ł—É—Ā –Ķ –Ĺ–Ķ–ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–į.¬†–ź –ĺ—ā –Ņ—Ä–ł–ľ–Ķ—Ä–į —Ā –Ņ–Ľ—ä–∑–≥–į—Č–ĺ—ā–ĺ —Ā–Ķ —É—Ā–ľ–ł—Ö–Ĺ–į—ā–ĺ –Ľ–ł—Ü–Ķ –Ņ–ĺ-–≥–ĺ—Ä–Ķ, —Ā–Ķ –≤–ł–∂–ī–į, —á–Ķ –ł –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ĺ–Ķ –Ķ¬†–ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–į.
–ü–ĺ–Ĺ—Ź—ā–ł–Ķ—ā–ĺ –ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–ĺ—Ā—ā –≤–į–∂–ł –ł –∑–į —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä –≤ –Ķ–ī–Ĺ–į –Ĺ–Ķ–ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É–Ķ–ľ–į —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–į –≤—Ā–Ķ–Ľ–Ķ–Ĺ–į –ľ–ĺ–∂–Ķ–ľ —ā–į–ļ–į –ī–į –Ņ–ĺ–ī—Ö–≤—ä—Ä–Ľ–ł–ľ –ī—Ź—Ā–Ĺ–į—ā–į —Ā–ł —Ä—ä–ļ–į–≤–ł—Ü–į, —á–Ķ –ī–į —Ā–Ķ –≤—ä—Ä–Ĺ–Ķ –ļ–į—ā–ĺ –Ľ—Ź–≤–į —Ä—ä–ļ–į–≤–ł—Ü–į!
–ź–ļ–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä–ł–ľ –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā–į –≤ –∑–į–≥–Ľ–į–≤–ł–Ķ—ā–ĺ - –ī–į, –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į–Ņ—ä–Ľ–Ĺ–ł –≤ –Ĺ–į—ą–ł—Ź —ā—Ä–ł–ľ–Ķ—Ä–Ķ–Ĺ —Ā–≤—Ź—ā –Ī—É—ā–ł–Ľ–ļ–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ, –Ĺ–ĺ –Ķ –ľ–Ĺ–ĺ–≥–ĺ —ā—Ä—É–ī–Ĺ–ĺ. –Ę–Ķ—á–Ĺ–ĺ—Ā—ā—ā–į —Ā—ä–∑–ī–į–≤–į –ī–ĺ–Ņ—ä–Ľ–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ĺ–į–Ľ—Ź–≥–į–Ĺ–Ķ –≤—ä—Ä—Ö—É –≤—ä–∑–ī—É—Ö–į –≤—ä—ā—Ä–Ķ, –į —ā–ĺ–Ļ –Ĺ—Ź–ľ–į –ļ—ä–ī–Ķ –ī–į —Ā–Ķ –ł–∑–ľ—ä–ļ–Ĺ–Ķ. –ė –ł–∑–Ľ–ł–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–Ķ—á–Ĺ–ĺ—Ā—ā—ā–į –Ķ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į —ā–Ķ—á–Ĺ–ĺ—Ā—ā—ā–į –≤ –Ī—É—ā–ł–Ľ–ļ–į—ā–į –Ĺ–į –ö–Ľ–į–Ļ–Ĺ –Ĺ–Ķ —Ā–Ķ –ł–∑–Ņ–į—Ä—Ź–≤–į, –į –ł –ī–į —Ā–Ķ –Ņ–ĺ—á–ł—Ā—ā—Ź—ā —Ā—ā–Ķ–Ĺ–ł—ā–Ķ –ĺ—ā–≤—ä—ā—Ä–Ķ –Ķ –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ. –Ě–ĺ —ā–į–ļ–į –ł–Ľ–ł –ł–Ĺ–į—á–Ķ, –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –Ĺ–Ķ¬†—Ź —Ü–Ķ–Ĺ—Ź—ā –∑–į—Ä–į–ī–ł –ļ–į—á–Ķ—Ā—ā–≤–į—ā–į –Ļ –Ĺ–į —Ā–Ķ—Ä–≤–ł–∑ –∑–į –≤–ł–Ĺ–ĺ.
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
Introducing the Klein bottle, Marianne Freiberger
Imaging maths - Inside the Klein bottle, Konrad Polthier





















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
14.06 2015 –≤ 18:55
–ě—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –Ņ—Ä–į–ļ—ā–ł—á–Ĺ–į –∑–į —Ü–Ķ–Ľ—ā–į –Ķ –Ķ—ā–ĺ —ā–į–∑–ł:
http://www.kleinbottle.com/drinking_mug_klein_bottle.htm
–Ē–Ķ–ī–ĺ –Ņ–ĺ–Ņ –≤—Ā–Ķ —Ā–Ķ –ļ–į–Ĺ–ł –ī–į —Ā–ł –Ņ–ĺ—Ä—ä—á–į.
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.
dolivo
–ó–Ķ–ľ–Ĺ–į—ā–į —Ź–Ī—ä–Ľ–ļ–į: —Ā—ā–į—Ä–į –ļ—É–Ľ—ā—É—Ä–į –∑–į –Ĺ–ĺ–≤–ł—ā–Ķ –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ĺ–į
dolivo
–ó–Ķ–ľ—Ź—ā–į –Ņ–ĺ—ā—ä–ľ–Ĺ—Ź–≤–į. –ö–į–ļ–≤–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į —ā–į–∑–ł —ā—Ä–Ķ–≤–ĺ–∂–Ĺ–į –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–į —ā–Ķ–Ĺ–ī–Ķ–Ĺ—Ü–ł—Ź –∑–į –Ī—ä–ī–Ķ—Č–Ķ—ā–ĺ?