

–Э–∞ –µ–і–љ–Њ –љ–Є–≤–Њ —И–∞—Е—К—В –Є–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –њ—А–Њ—Б—В–∞ –Є–≥—А–∞, –љ–Њ —А–∞–Ј—А–Њ–≤–µ—В–µ —Б–µ –Љ–∞–ї–Ї–Њ –њ–Њ-–і—К–ї–±–Њ–Ї–Њ –Є –Є–≥—А–∞—В–∞ –њ—А–µ–і–ї–∞–≥–∞ –љ–µ–≤–µ—А–Њ—П—В–љ–Њ —Б–ї–Њ–ґ–љ–Є –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є, –њ–Њ—Б—В–∞–≤—П–є–Ї–Є –њ—А–µ–і–Є–Ј–≤–Є–Ї–∞—В–µ–ї—Б—В–≤–∞ –њ—А–µ–і —И–∞—Е —В–µ–Њ—А–µ—В–Є—Ж–Є –Є –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –Њ—Б—В–∞–љ–∞—В –љ–µ—А–µ—И–µ–љ–Є –≤ –њ—А–Њ–і—К–ї–ґ–µ–љ–Є–µ –љ–∞ –і–µ—Б–µ—В–Є–ї–µ—В–Є—П –Є–ї–Є –і–Њ—А–Є –≤–µ–Ї–Њ–≤–µ.
–Я—А–µ–Ј —О–ї–Є 2021 –≥. –µ–і–љ–Њ —В–∞–Ї–Њ–≤–∞ –њ—А–µ–і–Є–Ј–≤–Є–Ї–∞—В–µ–ї—Б—В–≤–Њ –љ–∞–є-–љ–∞–Ї—А–∞—П –±–µ —А–µ—И–µ–љ–Њ вАУ –њ–Њ–љ–µ –і–Њ –Є–Ј–≤–µ—Б—В–љ–∞ —Б—В–µ–њ–µ–љ. –Ь–∞—В–µ–Љ–∞—В–Є–Ї—К—В –Ь–∞–є–Ї—К–ї –°–Є–Љ–Ї–Є–љ (Michael Simkin) –Њ—В –•–∞—А–≤–∞—А–і—Б–Ї–Є—П —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В –≤ –Ь–∞—Б–∞—З—Г–Ј–µ—В—Б —Б–µ –љ–∞—Б–Њ—З–≤–∞ –Ї—К–Љ –Ј–∞–і–∞—З–∞—В–∞ —Б n-—Ж–∞—А–Є—Ж–Є, –Ї–Њ—П—В–Њ –Њ–Ј–∞–і–∞—З–∞–≤–∞ –µ–Ї—Б–њ–µ—А—В–Є—В–µ, –Њ—В–Ї–∞–Ї—В–Њ –Ј–∞ –њ—К—А–≤–Є –њ—К—В –µ –±–Є–ї–∞ –њ—А–µ–і—Б—В–∞–≤–µ–љ–∞ –њ—А–µ–Ј 40-—В–µ –≥–Њ–і–Є–љ–Є –љ–∞ 19-—В–Є –≤–µ–Ї.
–¶–∞—А–Є—Ж–∞—В–∞ –µ –љ–∞–є-–Љ–Њ—Й–љ–∞—В–∞ —Д–Є–≥—Г—А–∞ –љ–∞ —И–∞—Е–Љ–∞—В–љ–∞—В–∞ –і—К—Б–Ї–∞. –Ч–∞ —А–∞–Ј–ї–Є–Ї–∞ –Њ—В –≤—Б—П–Ї–∞ –і—А—Г–≥–∞ (–≤–Ї–ї—О—З–Є—В–µ–ї–љ–Њ —Ж–∞—А—П), —В—П –Љ–Њ–ґ–µ –і–∞ —Б–µ –Љ–µ—Б—В–Є –љ–∞ –њ—А–Њ–Є–Ј–≤–Њ–ї–µ–љ –±—А–Њ–є –Ї–≤–∞–і—А–∞—В—З–µ—В–∞ –≤–µ—А—В–Є–Ї–∞–ї–љ–Њ, —Е–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–Њ –Є–ї–Є –і–Є–∞–≥–Њ–љ–∞–ї–љ–Њ.
–Ч–∞–і–∞—З–∞—В–∞¬†—Б n-—Ж–∞—А–Є—Ж–Є¬†—Б–µ —Б—К—Б—В–Њ–Є –≤¬†—Б–ї–µ–і–љ–Њ—В–Њ: –Я—А–Є –Њ–њ—А–µ–і–µ–ї–µ–љ –±—А–Њ–є —Ж–∞—А–Є—Ж–Є (n), –Ї–Њ–ї–Ї–Њ –њ–Њ–і—А–µ–ґ–і–∞–љ–Є—П —Б–∞ –≤—К–Ј–Љ–Њ–ґ–љ–Є, –њ—А–Є –Ї–Њ–Є—В–Њ —Ж–∞—А–Є—Ж–Є—В–µ —Б–∞ –і–Њ—Б—В–∞—В—К—З–љ–Њ –і–∞–ї–µ—З –µ–і–љ–∞ –Њ—В –і—А—Г–≥–∞, —В–∞–Ї–∞ —З–µ –љ–Є—В–Њ –µ–і–љ–∞ –Њ—В —В—П—Е –і–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞¬†–∞—В–∞–Ї—Г–≤–∞¬†–і—А—Г–≥–∞?
–Ч–∞ –Њ—Б–µ–Љ —Ж–∞—А–Є—Ж–Є –љ–∞ —Б—В–∞–љ–і–∞—А—В–љ–∞ –і—К—Б–Ї–∞ 8 x 8, –Њ—В–≥–Њ–≤–Њ—А—К—В –µ 92, –≤—К–њ—А–µ–Ї–Є —З–µ –њ–Њ–≤–µ—З–µ—В–Њ –Њ—В —В—П—Е —Б–∞ –Ј–∞–≤—К—А—В–µ–љ–Є –Є–ї–Є –Њ–≥–ї–µ–і–∞–ї–љ–Є –≤–∞—А–Є–∞–љ—В–Є –љ–∞ —Б–∞–Љ–Њ 12 –Њ—Б–љ–Њ–≤–љ–Є —А–µ—И–µ–љ–Є—П.
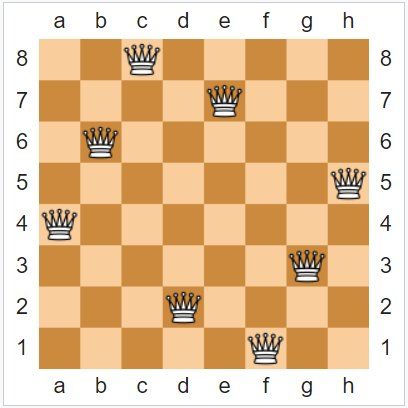 –Х–і–љ–Њ –Њ—В —А–µ—И–µ–љ–Є—П—В–∞ –Ј–∞¬†–Њ—Б–µ–Љ —Ж–∞—А–Є—Ж–Є –љ–∞ —Б—В–∞–љ–і–∞—А—В–љ–∞ –і—К—Б–Ї–∞ 8 x 8. –Ъ—А–µ–і–Є—В:¬†Wikimedia Commons¬†
–Х–і–љ–Њ –Њ—В —А–µ—И–µ–љ–Є—П—В–∞ –Ј–∞¬†–Њ—Б–µ–Љ —Ж–∞—А–Є—Ж–Є –љ–∞ —Б—В–∞–љ–і–∞—А—В–љ–∞ –і—К—Б–Ї–∞ 8 x 8. –Ъ—А–µ–і–Є—В:¬†Wikimedia Commons¬†
–Э–Њ –Ї–∞–Ї–≤–Њ¬†—Й–µ —Б—В–∞–љ–µ –Ј–∞ 1000 —Ж–∞—А–Є—Ж–Є –љ–∞ –і—К—Б–Ї–∞, –Ї–Њ—П—В–Њ –µ 1000 x 1000 –Ї–≤–∞–і—А–∞—В–∞? –Р–Љ–Є –Љ–Є–ї–Є–Њ–љ —Ж–∞—А–Є—Ж–Є?
–Ю—А–Є–≥–Є–љ–∞–ї–љ–∞—В–∞ –≤–µ—А—Б–Є—П –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—В–∞ –Ј–∞–і–∞—З–∞ —Б n-—Ж–∞—А–Є—Ж–Є¬†—Б–µ –њ–Њ—П–≤—П–≤–∞ –Ј–∞ –њ—К—А–≤–Є –њ—К—В –≤ –≥–µ—А–Љ–∞–љ—Б–Ї–Њ —И–∞—Е–Љ–∞—В–љ–Њ —Б–њ–Є—Б–∞–љ–Є–µ –њ—А–µ–Ј 1848 –≥. –Ї–∞—В–Њ –Ј–∞–і–∞—З–∞ –Ј–∞ –Њ—Б–µ–Љ—В–µ —Ж–∞—А–Є—Ж–Є, –∞ –њ—А–∞–≤–Є–ї–љ–Є—П—В –Њ—В–≥–Њ–≤–Њ—А —Б–µ –њ–Њ—П–≤—П–≤–∞ –љ—П–Ї–Њ–ї–Ї–Њ –≥–Њ–і–Є–љ–Є –њ–Њ-–Ї—К—Б–љ–Њ. –Ґ–Њ–≥–∞–≤–∞ –њ—А–µ–Ј 1869 –≥. —Б–µ –њ–Њ—П–≤—П–≤–∞ –њ–Њ-–Њ–±—И–Є—А–љ–∞—В–∞ –≤–µ—А—Б–Є—П –љ–∞ –Ј–∞–і–∞—З–∞—В–∞ –Є –Њ—Б—В–∞–≤–∞ –±–µ–Ј –Њ—В–≥–Њ–≤–Њ—А –і–Њ –Ї—А–∞—П –љ–∞ –Љ–Є–љ–∞–ї–∞—В–∞ –≥–Њ–і–Є–љ–∞, –Ї–Њ–≥–∞—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Њ—В –•–∞—А–≤–∞—А–і –і–∞–≤–∞ –њ–Њ—З—В–Є –Њ–Ї–Њ–љ—З–∞—В–µ–ї–µ–љ –Њ—В–≥–Њ–≤–Њ—А.
–Я—А–Є–±–ї–Є–Ј–Є—В–µ–ї–љ–Њ—В–Њ —А–µ—И–µ–љ–Є–µ –љ–∞ –°–Є–Љ–Ї–Є–љ –љ–∞ –Ј–∞–і–∞—З–∞—В–∞ –µ (0,143n)n, —В–Њ–µ—Б—В –±—А–Њ—П—В –љ–∞ —Ж–∞—А–Є—Ж–Є—В–µ, —Г–Љ–љ–Њ–ґ–µ–љ –њ–Њ 0,143, –њ–Њ–≤–і–Є–≥–љ–∞—В –љ–∞ —Б—В–µ–њ–µ–љ n.
–Ґ–Њ–≤–∞ –љ–µ –µ —В–Њ—З–љ–Є—П—В –Њ—В–≥–Њ–≤–Њ—А, –љ–Њ –µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ –љ–∞–є-–±–ї–Є–Ј–Њ –і–Њ –Љ–Њ–Љ–µ–љ—В–∞. –° –Љ–Є–ї–Є–Њ–љ —Ж–∞—А–Є—Ж–Є —Ж–Є—Д—А–∞—В–∞ –Є–Ј–ї–Є–Ј–∞ —З–Є—Б–ї–Њ —Б –њ–µ—В –Љ–Є–ї–Є–Њ–љ–∞ —Ж–Є—Д—А–Є —Б–ї–µ–і –љ–µ–≥–Њ вАУ —В–∞–Ї–∞ —З–µ –љ—П–Љ–∞ –і–∞ –≥–Њ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞–Љ–µ —В—Г–Ї.
–Э—Г–ґ–љ–Є —Б–∞ –±–Є–ї–Є¬†–њ–Њ—З—В–Є –њ–µ—В –≥–Њ–і–Є–љ–Є –љ–∞ –°–Є–Љ–Ї–Є–љ, –Ј–∞ –і–∞ –Є–Ј–ї–µ–Ј–µ —Б —Г—А–∞–≤–љ–µ–љ–Є–µ—В–Њ, —Б —А–∞–Ј–ї–Є—З–љ–Є –Є–Ј–њ–Њ–ї–Ј–≤–∞–љ–Є –њ–Њ–і—Е–Њ–і–Є –Є —В–µ—Е–љ–Є–Ї–Є –Є –љ—П–Ї–Њ–ї–Ї–Њ –±–∞—А–Є–µ—А–Є –њ–Њ –њ—К—В—П –Ї—К–Љ —А–µ—И–µ–љ–Є–µ—В–Њ. –Т –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї—К—В —Г—Б–њ—П–≤–∞ –і–∞ –Є–Ј—З–Є—Б–ї–Є –і–Њ–ї–љ–Є—В–µ –≥—А–∞–љ–Є—Ж–Є –Є –≥–Њ—А–љ–Є—В–µ –≥—А–∞–љ–Є—Ж–Є –љ–∞ –≤—К–Ј–Љ–Њ–ґ–љ–Є—В–µ —А–µ—И–µ–љ–Є—П, –Є–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є —А–∞–Ј–ї–Є—З–љ–Є –Љ–µ—В–Њ–і–Є, —Г—Б—В–∞–љ–Њ–≤—П–≤–∞–є–Ї–Є, —З–µ –њ–Њ—З—В–Є —Б—К–≤–њ–∞–і–∞—В.
–°–Є–Љ–Ї–Є–љ —Б–њ–Њ–і–µ–ї—П, —З–µ –ї–Є—З–љ–Њ —В–Њ–є –µ —Г–ґ–∞—Б–µ–љ —И–∞—Е–Љ–∞—В–Є—Б—В, –љ–Њ —Б–µ —Б—В—А–µ–Љ–Є –і–∞ –њ–Њ–і–Њ–±—А–Є –Є–≥—А–∞—В–∞ —Б–Є.
вАЮ–Т—Б–µ¬†–њ–∞–Ї —Б–µ —А–∞–і–≤–∞–Љ –љ–∞ –њ—А–µ–і–Є–Ј–≤–Є–Ї–∞—В–µ–ї—Б—В–≤–Њ—В–Њ –і–∞ –Є–≥—А–∞—П, –љ–Њ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–Љ, —З–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –µ –њ–Њ-–ї–µ—Б–љ–∞вАЬ, –Ї–Њ–Љ–µ–љ—В–Є—А–∞ –°–Є–Љ–Ї–Є–љ, –Ї–Њ–є—В–Њ —Б–µ –Є–љ—В–µ—А–µ—Б—Г–≤–∞ –Њ—В –њ—А–Њ–±–ї–µ–Љ–∞, –Ј–∞—Й–Њ—В–Њ –Љ–Њ–ґ–µ –і–∞ –њ—А–Є–ї–Њ–ґ–Є –њ—А–Њ–±–Є–≤–Є—В–µ¬†–≤ –Њ–±–ї–∞—Б—В—В–∞ –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞, –≤ –Ї–Њ—П—В–Њ —А–∞–±–Њ—В–Є, –љ–∞—А–µ—З–µ–љ–∞ –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–∞, –Ї–Њ—П—В–Њ —Б–µ —Д–Њ–Ї—Г—Б–Є—А–∞ –≤—К—А—Е—Г –±—А–Њ–µ–љ–µ –Є –њ—А–Њ–±–ї–µ–Љ–Є –љ–∞ –њ–Њ–і–±–Њ—А–∞ –Є –њ–Њ–і—А–µ–ґ–і–∞–љ–µ—В–Њ.
–°–њ—А–∞–≤–Ї–∞: Michael Simkin, The number of n-queens configurations. arXiv:2107.13460v2 [math.CO], arxiv.org/abs/2107.13460
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
Harvard mathematician answers 150-year-old chess problem
Juan Siliezar, Harvard University
A Harvard Mathematician Has Basically Solved an Epic, 150-Year-Old Chess Problem
DAVID NIELD, sciencealert





















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
24468
1
27.01 2022 –≤ 17:23
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
–•—А–Є—Б—В–Є—П–љ–Є–љ
–Ґ–Њ–≤–∞ –µ –Ї—А–∞–ї—П—В –љ–∞ —В–Є–Ї–≤–Є—В–µ: –Ґ–Є–Ї–≤–∞—В–∞ –Љ—Г —В–µ–ґ–Є –љ–∞–і –µ–і–Є–љ –µ–і–Є–љ —В–Њ–љ
dolivo
–°–∞—Е–∞—А–∞ –Њ—З–∞–Ї–≤–∞ 75% —Г–≤–µ–ї–Є—З–µ–љ–Є–µ –љ–∞ –≤–∞–ї–µ–ґ–Є—В–µ –і–Њ 2100 –≥.