Наградата Абел за 2025 г. бе присъдена на Масаки Кашивара от университета в Киото, Япония, за "неговите основни приноси към алгебричния анализ и теорията на представянията, по-специално развитието на теорията на D-модулите и откриването на кристалните основи", Звучи сложно и наистина е.
Но нека се опитаме да добием поне базова представа за какво става въпрос.
Симетриите
За да надникнем в областите на математиката, в които е работил проф. Кашивара, нека да започнем със симетриите. Ние сме склонни да мислим за симетриите по визуален начин, като трансформации, които оставят формата непроменена.
Като пример, може правоъгълник да се отрази огледално по неговите вертикална и хоризонтална ос и може да се завърти на 180 градуса, без да се променя начина, по който изглежда. Тези операции, заедно с операцията да не правиш нищо, са симетриите на правоъгълник.
Симетрията на правоъгълник: Може да отразите правоъгълник по неговата вертикална (червена) и хоризонтална (зелена) ос и може да го завъртите на 180 градуса, без да променяте външния му вид. Заедно с бездействието, това са симетриите на правоъгълник. Кредит: Plus Magazine
Симетриите, взети заедно, образуват самостоятелна система. Когато следвате една симетрия след друга, резултатът също е симетрия: например отразяването в хоризонталната ос и след това отразяването във вертикалната ос се равнява на завъртане на правоъгълника на 180 градуса (може да видите това, като маркирате ъглите на правоъгълника и видите къде остават накрая във всеки един от случаите). Всяка симетрия в тази колекция също може да бъде "отменена": в нашия пример, извършването на индивидуална симетрия два пъти връща всяка точка от правоъгълника там, където е започнала.
Структурата в рамките на колекцията от симетрии означава, че те образуват това, което математикът нарича група. Една група се определя от определен набор от правила.
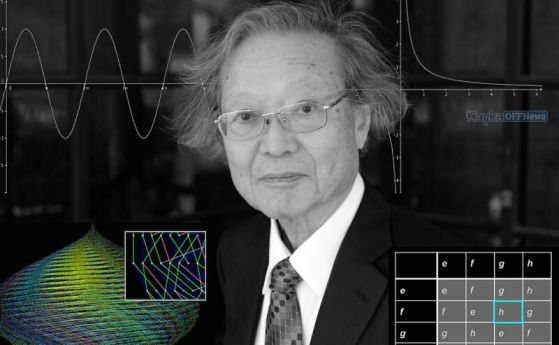
Да се проследи това, което се получава след всяко симетрично преобразувание, е малко досадно, но може да си направим удобна таблица, като тази, показана по-долу. Означавайки отраженията и въртенето, както в изображението по-горе, записът, съответстващ например на ред с етикет f и колона с етикет g, ни показва каква цялостна симетрия получаваме, когато приложите g, последвано от f — в този случай това е h.
Кредит: Plus Magazine
В тази таблица буквите означават симетриите на правоъгълника, както е отбелязано на фигурата по-горе. Буквата e означава симетрията, която се състои в неправене на нищо.
Скок в абстракцията
Има други математически обекти, които не са (за необученото око) симетрични на нищо, но които също могат да образуват групи. Примери за такива са матриците, масиви от числа, които могат да бъдат умножени заедно, така че резултатът също винаги да е матрица. Когато маркирате членовете на такава колекция с букви и конструирате таблица, както направихме по-горе, може да откриете, че таблицата изглежда точно същата като тази, идваща от групата симетрия на правоъгълника. (Прочетете "Симетриите като групи" и "Теорията на групите - една усмивка само")
Това ни дава възможност да скочим в абстракцията - може да си представим групите не като колекции от определени неща, а като колекция от абстрактни обекти, които си взаимодействат по начин, предписан от таблица с букви. Това, което определя групата, не е природата на нещата, които я съставят, а начинът, по който те си взаимодействат.
Това вече е алгебра. Тук изследвате структурата на колекции от абстрактни обекти. Съществуват и други видове колекции с различна структура. Например, в математически пръстен нямате просто един начин за комбиниране на два от нашите абстрактни обекти, а два (аналогично на събиране и умножение на числа).
Силата на тази абстракция се крие във факта, че след като разберем нещо за нашата абстрактна колекция от неща, това знание може да се прилага към всяка колекция от конкретни неща - било то симетрии на форма, матрици или нещо друго, което пасва на картината.
Диференциалните уравнения - да уловиш промяната
От тези високи висини на абстракцията нека сега се върнем долу в реалния свят. До голяма степен той се характеризира с промрни - нещата се движат, растат и се развиват и по други начини. Можем да се опитаме да опишем тази промяна математически и да използваме описанието, за да направим прогнози: ако сте забелязали, че парите в банковата ви сметка нарастват с 1000 лв всеки месец, тогава може да използвате това, за да предвидите, че след една година ще бъдете с 12 x 1000 = 12 000 по-добре финансово.
За да се направят прогнози, трябва да се реши диференциалното уравнение, което описва промяната. Решението ще определи колко голяма ще бъде въпросната величина в даден момент във времето (или пространството, или за дадена стойност на друга референтна величина).
Диференциални уравнения се появяват почти винаги, когато се прилага математика за решаване на проблеми от реалния свят - във физиката, биологията, химията, икономиката и инженерството... и това не са всички области. Проблемът е, че диференциалните уравнения обикновено са сложни и често невероятно трудни, дори невъзможни, за решаване.
На математиците това, че са трудни, им харесва. Ето защо диференциалните уравнения формират поле за изследване сами по себе си. Хората ги изследват, без да се позовават на проблема от реалния живот, в който възникват, и дори изследват уравнения, които не произтичат от никакъв проблем от реалния свят. За да се опишат и да се пресметне докъде ще доведат промените, се разглеждат безкрайно малки количества, граници и други подобни. Това са някои от инструментите на математическия анализ.
Областта на математиката, която дава формална основа на инструментите от математическия анализ, гарантирайки, че всичко е логично, правилно и доказано, се нарича анализ.
Алгебричен анализ
Досега представените две области, алгебра и анализ, изглеждат доста различни - алгебрата е възвишена и абстрактна, а анализът малко по-сложен и хаотичен, неподреден. Но външният вид лъже и имат важни връзки.
Анализът се занимава с математически обекти като функции . Пример е функцията ƒ(x) = 1000x, която срещнахме по-горе, изразяваща сумата пари, която ще спечелите след x месеца, ако богатството ви се увеличава с 1000 лв на месец.
Разгледани като математически обекти, функциите могат да се комбинират (например може да се прилагат една функция след друга, като общият резултат също е функция), така че може да се разглеждат колекции от функции точно както разгледахме колекции от симетрии по-горе. Такива колекции могат също да образуват алгебрични структури като групи или пръстени. Същото важи и за неща като диференциални оператори, които свързват различни функции със скоростите на промяна.
По този начин се създава връзка между алгебрата и анализа. Областта на алгебричния анализ използва тази връзка, за да решава проблеми, свързани с диференциални уравнения, като използва алгебра. Хората използват силата на алгебрата в този контекст от доста дълго време, но заслугата за утвърждаването на алгебричния анализ като систематична област на изследване е на японския математик Микио Сато (Mikio Sato).
Кашивара се запознава със Сато в Токийския университет през 70-те години на миналия век и завършва магистърската си теза под ръководството на Сато. В тази дисертация, на крехката възраст от 23 години, Кашивара разработва теорията на D-модулите. Тези обекти, по същество алгебрични структури, свързани с диференциални уравнения, се превръщат във фундаментален компонент на алгебричния анализ и се оказват невероятно мощен инструмент в много области на математиката. (Ако искате техническо въведение, може да прочетете магистърската теза на Кашивара).
D-модулите
Важен пример за вида пътища, които D-модулите са отворили, идва от един проблем, поставен от математика Давид Хилберт през 1900 г. на Международния конгрес на математиците в Париж. Задачата на Риман-Хилберт е 21-ва в списъка от 23 задачи, които според Хилберт ще определят дневния ред на изследванията в математиката през ХХ век. В рамките на общия дух на анализа проблемът задава въпроса дали съществува клас от диференциални уравнения, които всички отговарят на определен набор от характеристики. Да се опитаме да обясним.
Може би си спомняте от училище, че е възможно едно уравнение да има множество решения. Например уравнението sin(x) = 0 има решенията: 0, π, 2π, ... kπ
Кредит: Plus Magazine
Тази многозначност е особен проблем, ако се появи около нещо, наречено сингулярност, точка, в която уравнението се държи странно, вместо да варира редовно, както се случва за функцията синус. Например функцията 1/x има особеност при x = 0, където е неопределена. За много малки отрицателни стойности на x функцията има много голяма отрицателна стойност и за много малки положителни стойности на x има много голяма положителна стойност.
Математиците използват нещо, наречено монодромна група на уравнение, за да разберат това странно поведение. Тази група описва топологията – или формата – на пространство, което възниква от начина, по който решенията на уравнението се променят близо до сингулярността.
Всеки тип диференциални уравнения, наречени линейни диференциални уравнения, има свързана монодромна група. Но проблемът на Риман-Хилберт пита за другата посока: за всяка монодромна група има ли свързано линейно диференциално уравнение, чието поведение в близост до сингулярност се описва от тази група?
Казусът за уравнения, включващи една променлива, е решен през 60-те години. През 80-те години Кашивара показва как да се намери свързаното линейно диференциално уравнение за всяка монодромна група, всъщност Кашивара формулира и доказва резултати в значително по-обща постановка от първоначално предложената от Хилберт.
Кашивара продължава да работи в тази област и днес и заедно с Андреа Д'Аньоло не отдавна са направили важни допълнения към работата му, произтичащи от проблема на Риман-Хилберт.
Представяне на абстрактни структури
Работата на Кашивара, вдъхновена от проблема на Риман-Хилберт, се свързва с теорията на представянията (representation theory), другата област, спомената в горния цитат, освен алгебричния анализ.
Теорията на представянията ни връща към началото на тази статия, когато разглеждахме алгебричните групи. Отбелязахме, че групите могат да се разглеждат като колекции от абстрактни неща. Не е необходимо да знаем какви точно са тези неща - начинът, по който те си взаимодействат, определя групата.
Тази абстракция е прекрасна, но може да бъде и твърде гъвкава. Когато работите с група, може да е полезно да знаете кои точно са нещата, които я изграждат. А когато работите с повече от една група, може да е полезно, ако нещата, които ги съставят, са от един и същи тип - трудно е да се сравняват ябълки с портокали.
Математическата природа е била благосклонна към математиците в това отношение. Оказва се, че много групи, особено тези, които се състоят от крайно много неща, могат да се разглеждат като съставени от матрици: онези масиви от числа, за които вече споменахме по-рано (вижте тук, за да научите повече). Например отраженията и завъртанията на равнината, като тези, които дават симетриите на правоъгълника, могат да бъдат представени чрез матрици, които имат четири записа, подредени в два реда по два. Те могат да се интерпретират като трансформации на равнината (технически матриците могат да действат върху векторни пространства).
В по-общ план, когато ви е дадена абстрактна група, има голяма вероятност да намерите набор от матрици, които заедно образуват точно тази група. Това е късмет, защото математиците разбират матриците особено добре.
Теорията на представянията е изучаването на групите и други алгебрични структури от гледна точка на матрици, действащи върху векторни пространства. Това е важна област на изследване, която е полезна в много други области на математиката. Теорията на D-модулите на Кашивара се оказа изключително полезна в теорията на представянията.
В още едно постижение за осъществяване на връзки и вдъхновен от проблеми, възникнали в теоретичната физика, Кашивара въвежда и идеята за кристални основи в теорията на представянето. Тези обекти позволяват да се отговори на въпроси от теорията на представянето с помощта на комбинаториката - изкуството да се доказват резултати чрез броене на аргументи. По-специално, Кашивара разкрива сърцевината на сложните математически структури (представени като матрици, действащи върху векторни пространства), които са графи. Върховете на тези кристални графи са основата – "атомните елементи" – на математическата структура, а краищата показват как тези атомни елементи са взаимосвързани.
Кристалните основи намират приложение и в теорията на числата и дори в статистическата физика.
Пример за кристална основа. Кристалните основи са използвани за доказване на формули за статистическото поведение на системи от частици. Изобразено с помощта на CrystalView. Кредит: Anne Schilling и Philip Starhill)
Това, разбира се, е само малка част от темите на работата на Кашивара и нейните дълбоки последици за математиката.
Работата на Кашивара, както и тази други изключителни математици, свързва светове. В училище обикновено ни учат, че математиката се разделя на различни области: геометрия, алгебра и математически анализ например. Всъщност обаче всички те са свързани - и често когато някой намери начин да приложи методи от една област в друга, математиката се отваря за нови постижения. Кашивара е направил точно това и неговата работа има дълбоки последици за математиката. В цитата за наградата Абел се казва:
"Кашивара е изключително плодовит математик с повече от седемдесет сътрудници. В продължение на повече от петдесет години той прекрои и дълбоко обогати полетата на теорията на представянето, в нейните многобройни превъплъщения, и алгебричния анализ. Неговата работа продължава да бъде в челните редици на съвременната математика и да вдъхновява поколения изследователи."
Източници:
The Abel Prize 2025: Masaki Kashiwara, Marianne Freiberger, Plus Magazine, University of Cambridge
The Chern Medal 2018: Masaki Kashiwara, Rachel Thomas, Plus Magazine, University of Cambridge
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
dolivo
Полетът на Starliner до МКС през 2024 г. е бил много по-драматичен, отколкото знаем (видео)
dolivo
Загадка: Как са се озовали инструменти, подобни на неандерталските, в Източна Азия - разстоянието е континент?
dolivo
Варна става част от Световно космическо парти с кратки видеоклипове и техно груув парти
Имане Хелиф
Анусът може да е еволюирал от отвор, първо използван за отделяне на сперма