Задачата за четирите цвята е лесна за обяснение, но сложното ѝ доказателство продължава да е оспорвано и само компютрите могат да решат тази задача за оцветяване на карта от началото на 19-ти век.
На 23 октомври 1852 г. започва един от най-великите епизоди в историята на математиката. В писмо до сър Уилям Роуън Хамилтън Огъстъс де Морган пише: "Днес един мой ученик ме помоли да му дам основание за един факт, за който не знаех, че е факт - и все още не знам." И до днес този "факт" продължава да вълнува и предизвиква учените.
Ученикът се казвал Фредерик Гътри, а въпросният "факт" първоначално дошъл от неговия брат Франсис. След като разгледал карта на британските графства, той се запитал дали винаги е възможно картата да бъде оцветена с четири или по-малко цвята, като се гарантира, че регионите, които имат обща граница (повече от една ъглова точка), са с различни цветове.
Изглеждаше, че това винаги трябва да е възможно. "Колкото повече мисля за това, толкова по-очевидно ми се струва", пише Де Морган. Въпреки това проблемът не развълнувал Хамилтън. Той отговорил: "Едва ли скоро ще се заема да опитам Вашия "кватернион на цветовете". Усилията на Де Морган да заинтересува други също се провалят.
Проблемът остава почти незасегнат до 1878 г., когато Артър Кейли пита членовете на Лондонското математическо общество дали някой е намерил доказателство. Скоро след това започват да се появяват доказателства. Първото от тях, направено от адвоката Алфред Кемпе през 1879 г., се оказва най-важното. Доказателството е убедително и се приема за правилно в продължение на повече от десетилетие. За съжаление доказателството на Кемпе - както и всички останали, които се появяват през следващия век - е погрешно. Въпреки това то е гениално и съдържа ключови идеи, които ще се появят в окончателното доказателство.
За да разберем как Кемпе и повечето математици са разглеждали този проблем, е полезно да осъзнаем, че картата съдържа много информация, която няма отношение към проблема с оцветяването, като например формата, размера и точното местоположение на всеки регион. Единственото, което има значение, е кои региони имат общи граници, въпреки че изискваме всички региони да са свързани.
За да се съсредоточим върху важната информация, можем да кодираме тези взаимоотношения с помощта на граф, известен още като мрежа, където точките (върховете) са свързани с линии (ребрата). Заменете всеки регион на картата с връх и свържете върховете на съседните региони с ръб. Ако това помага, можем да си представим, че върховете са столиците, а ребрата са пътищата, които ги свързват.
По този начин задачата за оцветяване на карта се превръща в задача за оцветяване на граф: Оцветете върховете така, че съседите да са с различни цветове. Минималният брой цветове се нарича хроматично число на графа.
Можем да попитаме за хроматичното число на всеки граф, но графите, които произлизат от карти, имат специални свойства. Тези графи са прости, което означава, че няма ребра, започващи и завършващи на един и същи връх (наречени примки), и два върха могат да бъдат свързани само с едно ребро. Графът е и равнинен, което означава, че трябва да бъде начертан така, че да няма пресичащи се ребра.
Задачата за оцветяване на карта може да се трансформира в задача за оцветяване на граф.
Сега можем да преформулираме задачата на Франсис Гътри: Докажете, че хроматичното число на всеки прост планарен граф е най-много четири.
Ето една скица на аргумента на Кемпе, описан на съвременен език, като се използват графи, а не карти. Той започва с наблюдението, че граф с един връх - може би картата е самотен остров - изисква само един цвят. След това използва хитър аргумент, за да се издигне нагоре оттам, твърдейки, че е възможно да се използват най-много четири цвята, за да се оцвети граф с два върха, след това с три върха и т.н. Ето как.
Да предположим, че можем да оцветим всички прости равнинни графи с n върха с най-много четири цвята - това е тривиално за n < 5 - и след това ни се предоставя един с n + 1 върха. Как можем да покажем, че и той ще може да се оцветява с най-много четири цвята?
Първо, Кемпе показа, използвайки внимателно аргумент за броене, че всеки прост плосък граф има нещо общо: той трябва да съдържа поне един връх с най-много пет съседа. Като се вземат предвид всички възможности, това означава, че всеки възможен граф, основан на карта, съдържа една от шестте специални конфигурации на върховете.
Въпреки че е описан с помощта на карти, а не на графи, Алфред Кемпе доказва, че всеки прост планарен граф трябва да има връх от един от тези типове.
Ако премахнем този връх и всички ребра, които се свързват с него, ще получим граф с n върха, за който вече знаем, че може да бъде оцветен с четири цвята. Всъщност ще го направим като следваща стъпка. Сега погледнете върховете, съседни на премахнатия връх. Ако в тях има три или по-малко цвята, можем да оцветим премахнатия връх с един от останалите цветове и сме готови: Току-що показахме, че графът с n + 1 върха може да бъде оцветен с четири цвята. А ако съседните върхове включват всичките четири цвята, Кемпе е разработил хитър метод за преоцветяване на определени върхове, за да освободи цвят за премахнатия връх, като отново показва, че графът с n + 1 върха се нуждае само от четири цвята.
През 1890 г. математикът Пърси Хийуeд (Percy Heawood) установява грешката на Кемпе. Съществувал е специален случай, в който умният метод на Кемпе не е успял. Хийуeд отбелязва, че макар собствената му работа да изглежда "по-скоро деструктивна, отколкото конструктивна", той показва, че техниката на Кемпе може да докаже, че всяка карта може да бъде оцветена с пет или по-малко цвята - не съвсем според първоначалната цел, но все пак впечатляващо.
Хийуeд също така изследва карти, начертани върху по-сложни повърхности. Той доказа, че карта върху поничка с g дупки може да се нуждае от:
 |
цветове (където тази стойност се закръгля до най-близкото цяло число) |
Така че украсяването на обикновена поничка може да изисква 7 цвята глазура. И все пак, което се превръща в обичайно явление, доказателството му за общи повърхности е непълно и до 1968 г. не разполагаме с пълно доказателство.
За тази карта на поничка, показана от двете страни, всяка от седемте области граничи с другите шест области, така че са необходими седем цвята.
Но дори когато теоремата на Хийуeд за общите повърхности бе доказана, проблемът с четирите цвята остаwа нерешен. Благодарение на десетилетия упорита работа обаче доказателството е налице.
На конференция през 1976 г., 124 години след като Гътри поставя проблема, Волфганг Хакен (Wolfgang Haken) обявява доказателство в сътрудничество с Кенет Апел (Kenneth Appel) и с помощта на дипломанта Джон Кох (John Koch). Реакциите били смесени. "Очаквах аудиторията да избухне в бурни овации", пише Дон Албърс (Don Albers), който присъства на доклада. "Вместо това реагираха с учтиви аплодисменти!" Причината била, че вместо да изготви аргумент с молив и хартия, екипът разчиташе в голяма степен на компютър.
Те не са имали машина, която да може отговори директно на въпроса, тъй като са възможни безкрайно много планарни графи и компютърът не може да провери всички. Въпреки това, както Кемпе доказва, че всеки граф съдържа една от шестте специални конфигурации на върховете, Апел и Хакен показват, че всеки граф трябва да има една от 1936 специални конфигурации. Доказването на теоремата е равносилно на това да покажем, че се нуждаем само от четири цвята, за да оцветим всеки граф, съдържащ тези подграфи. Разбиването на шестте специални случая на Кемпе на 1 936 подслучая им дава по-прецизен контрол и улеснява проверката на всеки случай - въпреки че общият брой вече е твърде голям, за да може човек да го провери без чужда помощ. Всъщност за завършването на изчисленията са били необходими над 1000 часа компютърно време.
Математическата общност приема резултатите с неохота, тъй като смята, че едно доказателство трябва да бъде разбираемо и проверимо изцяло от човек. Макар да е приемливо компютрите да извършват рутинни аритметични действия, математиците не са готови да отстъпят логическото мислене на компютърно устройство. Този консерватизъм и нежелание да се възприемат постиженията, които пестят време, не са нещо ново. През XVII в. подобно недоволство е имало, когато някои математици са използвали нови алгебрични техники за решаване на задачи в геометрията. Подобна драма може да се разиграе отново с възхода на машинното обучение: Ще приемат ли математиците теорема, открита и доказана от непрозрачен алгоритъм?
Доказателството на задачата за четирите цвята, разбира се, е само началото на компютърната революция в математиката. През 1998 г. Томас Хейлс (Thomas Hales) използва компютър, за да докаже известното предположение на Йоханес Кеплер, че най-ефективният начин за подреждане на сфери е този, който се използва за подреждане на портокали в магазин за хранителни стоки.
Въпреки че проблемът с четирите цвята на картите е решен, много основни въпроси за оцветяването на графите остават без отговор или едва сега се разрешават.
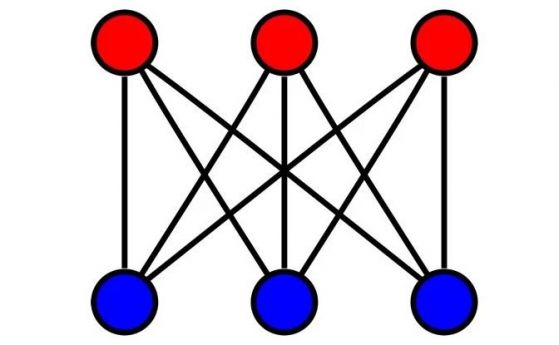
Работата на Хийуeд с повърхности показва, че можем да задаваме въпроси за оцветяване на непланарни графи. И всъщност хроматичното число на даден граф не зависи от повърхността, върху която е начертана еквивалентната карта. Например граф, в който всеки връх е свързан с всеки друг връх, се нарича пълен граф, а хроматичното число на пълен граф с n върха е n. Така че ако голям граф съдържа пълен граф с n върха, тогава знаем, че хроматичното число на големия граф е поне n.
Пълен граф с n върха има хроматично число n.
Това наблюдение не означава, че ако хроматичното число на даден граф е n, то той съдържа пълен граф с n върха. Но през 1943 г. Хуго Хадвигер изказва подобно предположение. Той смята, че ако един граф без примки има хроматично число n, то той има подредба на върховете, наречена Knминор, при което заличаването на някои върхове и ребра и групирането на други води до пълен граф с n върха. ("Минор" в линейната алгебра е детерминантата на някаква по-малка квадратна матрица B, изрязани от дадената матрица A чрез отстраняване на един или повече от нейните редове и колони.)
Преформулирано, това предположение гласи, че ако графът няма Knминор, то той може да бъде оцветен с по-малко от n цвята. Хипотезата на Хадвигер, един от най-важните открити проблеми в теорията на графите, обобщава теоремата за четирите цвята, тъй като един плосък граф не може да съдържа K5минор.
Въпреки че оцветяването на графите започва с въпрос в картографията, проблеми, които нямат нищо общо с карти или цветове, също могат да се впишат в рамката на оцветяването на графите. Например судоку е прикрита задача за оцветяване на графи. Може да се гледа на всяка клетка като връх, а на деветте цифри - като цветове. Всеки връх има 20 ръба, които излизат от него - по един към всяка клетка в реда, в колоната и в квадратчетата 3 на 3. Този граф от 81 върха и 810 ребра започва с частично оцветяване (дадените подсказки). Целта на играта е да оцветите останалите върхове.
Судоку може да се разглежда като задача за оцветяване на граф.
Въпреки цялото внимание, което са получили тези задачки за оцветяване, все още не разполагаме с доказателство на оригиналната теорема за четирите цвята, което човек да може да прочете. Това не се дължи на липса на опити. Дори и днес се появяват нови доказателства, които предизвикват известен ентусиазъм и, подобно на доказателството на Кемпе, се оказва, че съдържат грешки.
Свързани статии:
Нов алгоритъм обещава да опрости проблема за "изоморфизма на графите"
Не стигат четири цвята да се боядиса равнина
Стара математическа загадка е окончателно решена
Числата на Рамзи: Какви гости да си поканим на парти
Източник: The Colorful Problem That Has Long Frustrated Mathematicians, Quanta magazine
А това е отговорът на читателски въпрос 1:
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари