

–ė–∑—á–ł—Ā–Ľ—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —á–ł—Ā–Ľ–į—ā–į –Ĺ–į –†–į–ľ–∑–ł –Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į —ā—Ä—É–ī–Ĺ–ĺ, —á–Ķ –Ķ–ī–ł–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –≤–Ķ–ī–Ĺ—ä–∂ –ļ–į–∑–≤–į, —á–Ķ –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į –ī–į —Ā–Ķ –Ī–ĺ—Ä–ł —Ā –Ĺ–į—ą–Ķ—Ā—ā–≤–ł–Ķ –Ĺ–į –ł–∑–≤—ä–Ĺ–∑–Ķ–ľ–Ĺ–ł. –°–Ķ–≥–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ —Ā–į –Ņ–ĺ—Ā—ā–ł–≥–Ĺ–į–Ľ–ł –Ņ—ä—Ä–≤–ł—Ź –≥–ĺ–Ľ—Ź–ľ –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ –ĺ—ā –Ī–Ľ–ł–∑–ĺ –≤–Ķ–ļ –Ĺ–į—Ā–į–ľ.
–ü—Ä–Ķ–∑ 1928 –≥. –§—Ä–į–Ĺ–ļ –†–į–ľ–∑–ł —Ā–Ķ –Ī–ĺ—Ä–ł —Ā –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—ā–į –Ľ–ĺ–≥–ł–ļ–į. –°—ā—Ä—É–≤–į –ľ—É —Ā–Ķ, —á–Ķ –∑–į –ī–į –≥–ĺ —Ä–Ķ—ą–ł, —ā—Ä—Ź–Ī–≤–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ, —á–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—ā–Ķ —Ā–ł—Ā—ā–Ķ–ľ–ł, –ļ–ĺ–ł—ā–ĺ –ł–∑—É—á–į–≤–į, –≤–ł–Ĺ–į–≥–ł –ł–ľ–į—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ —Ä–Ķ–ī. –Ě–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī —Ā–ł—Ā—ā–Ķ–ľ–ł—ā–Ķ –ľ–ĺ–∂–Ķ–Ľ–ł –ī–į –Ī—ä–ī–į—ā –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ —Ā–ł –ł—Ā–ļ–į—ā —Ö–į–ĺ—ā–ł—á–Ĺ–ł, –Ĺ–ĺ –†–į–ľ–∑–ł —Ā–ľ—Ź—ā–į–Ľ, —á–Ķ –ī–ĺ—Ä–ł –ł –≤ –Ĺ–į–Ļ-–Ĺ–Ķ–Ņ–ĺ–ļ–ĺ—Ä–Ĺ–ł—ā–Ķ, —Ā–į–ľ–ł—Ź—ā —Ä–į–∑–ľ–Ķ—Ä –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į –Ī–ł —ā—Ä—Ź–Ī–≤–į–Ľ–ĺ –ī–į –Ņ—Ä–ł–Ĺ—É–ī–ł —á–į—Ā—ā–ł –ĺ—ā –Ĺ–Ķ—Ź –ī–į –Ņ—Ä–ĺ—Ź–≤—Ź–≤–į—ā –Ĺ—Ź–ļ–į–ļ—ä–≤ —Ä–Ķ–ī.
–Ē–ĺ–ļ–į–∑–≤–į–Ļ–ļ–ł, —á–Ķ –ł–Ĺ—ā—É–ł—Ü–ł—Ź—ā–į –ľ—É –Ķ –≤—Ź—Ä–Ĺ–į, —ā–ĺ–Ļ –ł–∑–ĺ–Ī—Ä–Ķ—ā—Ź–≤–į –Ĺ–ĺ–≤ –ļ–Ľ–ĺ–Ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ–≥–į –Ķ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –ļ–į—ā–ĺ —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –†–į–ľ–∑–ł. –Ę–ĺ–Ļ –Ņ—Ä–ĺ—á–ł—ā–į —Ā—ā–į—ā–ł—Ź—ā–į —Ā–ł –Ņ—Ä–Ķ–ī –õ–ĺ–Ĺ–ī–ĺ–Ĺ—Ā–ļ–ĺ—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ –ĺ–Ī—Č–Ķ—Ā—ā–≤–ĺ, –Ĺ–ĺ —É–ľ–ł—Ä–į –Ĺ–į 26-–≥–ĺ–ī–ł—ą–Ĺ–į –≤—ä–∑—Ä–į—Ā—ā, –Ņ—Ä–Ķ–ī–ł —ā—Ź –ī–į –Ī—ä–ī–Ķ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–į –≤ –Ĺ–Ķ–≥–ĺ–≤–ł—Ź —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ.
–Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł –≤—Ā–Ķ –ĺ—Č–Ķ –Ĺ–į–ľ–ł—Ä–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –≤ –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į –Ľ–ĺ–≥–ł–ļ–į—ā–į. –Ě–ĺ —ā—Ź –Ķ –ł –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ł–≤–Ľ–Ķ–ļ–į—ā–Ķ–Ľ–Ĺ–į —ā–Ķ–ľ–į —Ā–į–ľ–į –Ņ–ĺ —Ā–Ķ–Ī–Ķ —Ā–ł, —ā—ä–Ļ –ļ–į—ā–ĺ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ł—ā–Ķ —Ě –ł–ī–Ķ–ł –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā —Ä–į–∑–Ī—Ä–į–Ĺ–ł –ľ–Ĺ–ĺ–≥–ĺ –Ľ–Ķ—Ā–Ĺ–ĺ –ł –≤–ļ–Ľ—é—á–≤–į—ā —Ä–ł—Ā—É–≤–į–Ĺ–Ķ –Ĺ–į —Ü–≤–Ķ—ā–Ĺ–ł –ļ–į—Ä—ā–ł–Ĺ–ļ–ł. –ě—ā –ī—Ä—É–≥–į —Ā—ā—Ä–į–Ĺ–į, —ā—Ź –Ķ –ł –į–ļ—ā–ł–≤–Ĺ–į –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ā–ļ–į –ĺ–Ī–Ľ–į—Ā—ā, —ā—ä–Ļ –ļ–į—ā–ĺ –Ņ–ĺ–≤–ī–ł–≥–į –Ĺ—Ź–ļ–ĺ–ł –≤–Ņ–Ķ—á–į—ā–Ľ—Ź–≤–į—Č–ĺ —ā—Ä—É–ī–Ĺ–ł –≤—ä–Ņ—Ä–ĺ—Ā–ł. –ö–ĺ–≥–į—ā–ĺ –Ņ—Ä–Ķ–∑ 1998 –≥. –Ī–Ķ—ą–Ķ –ĺ–Ī—Ź–≤–Ķ–Ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—Ź—ā –ļ—Ä—ä–≥ –ĺ—ā –§–ł–Ļ–Ľ–ī—Ā–ĺ–≤–ł—ā–Ķ –ľ–Ķ–ī–į–Ľ–ł - –§–ł–Ļ–Ľ–ī—Ā –Ķ –Ĺ–į–Ļ-–Ņ—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į—ā–į –Ĺ–į–≥—Ä–į–ī–į –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –Ĺ–į–Ļ-–Ī–Ľ–ł–∑–ļ–ł—Ź—ā –Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā –Ĺ–į –Ě–ĺ–Ī–Ķ–Ľ–ĺ–≤–į—ā–į –Ĺ–į–≥—Ä–į–ī–į - –Ķ–ī–ł–Ĺ –ĺ—ā —ā—Ź—Ö –ĺ—ā–ł–ī–Ķ –Ņ—Ä–ł –Ī—Ä–ł—ā–į–Ĺ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ę–ł–ľ –ď–į—É—ä—Ä—Ā, –ĺ—ā—á–į—Ā—ā–ł –∑–į —Ä–į–Ī–ĺ—ā–į—ā–į –ľ—É –≤ –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł. –í —ā–į–∑–ł —Ā—ā–į—ā–ł—Ź —Č–Ķ –≤–ł–ī–ł–ľ, —á–Ķ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł –ł–ľ–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—ā–į –ī–į –∑–į–ī–į–≤–į –ī–ĺ—Ä–ł –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā–ł –Ĺ–į –≤–ł–ī –≤—ä–Ņ—Ä–ĺ—Ā–ł, –ļ–ĺ–ł—ā–ĺ –ī–ĺ—Ā–Ķ–≥–į —Ā–į —Ā–Ķ –ł–∑–Ņ–Ľ—ä–∑–≤–į–Ľ–ł –Ĺ–į –≤—Ā–ł—á–ļ–ł –ĺ–Ņ–ł—ā–ł –ī–į –ł–ľ —Ā–Ķ –ĺ—ā–≥–ĺ–≤–ĺ—Ä–ł.
–†–Ķ–ī –ĺ—ā —Ö–į–ĺ—Ā–į
–§—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–ł—Ź—ā –≤—ä–Ņ—Ä–ĺ—Ā, –ļ–ĺ–Ļ—ā–ĺ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł –∑–į–ī–į–≤–į, –Ķ: –ľ–ĺ–∂–Ķ –Ľ–ł –≤–ł–Ĺ–į–≥–ł –ī–į —Ā–Ķ –Ĺ–į–ľ–Ķ—Ä–ł —Ä–Ķ–ī –≤ —Ö–į–ĺ—Ā–į? –ź–ļ–ĺ –Ķ —ā–į–ļ–į, –ļ–ĺ–Ľ–ļ–ĺ? –ö–ĺ–Ľ–ļ–ĺ –≥–ĺ–Ľ—Ź–ľ–ĺ –Ņ–į—Ä—á–Ķ –ĺ—ā —Ö–į–ĺ—Ā–į –Ĺ–ł –Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ, –∑–į –ī–į —Ā–ľ–Ķ —Ā–ł–≥—É—Ä–Ĺ–ł, —á–Ķ –≤ –Ĺ–Ķ–≥–ĺ —Č–Ķ –ĺ—ā–ļ—Ä–ł–Ķ–ľ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —Ä–Ķ–ī? –Ę—É–ļ, –ļ–ĺ–≥–į—ā–ĺ –≥–ĺ–≤–ĺ—Ä–ł–ľ –∑–į "—Ö–į–ĺ—Ā" –≤ —ā–į–∑–ł —Ā—ā–į—ā–ł—Ź, –ł–ľ–į–ľ–Ķ –Ņ—Ä–Ķ–ī–≤–ł–ī –Ņ—Ä–ĺ—Ā—ā–ĺ –Ĺ–Ķ—Č–ĺ —Ä–į–∑—Ö–≤—ä—Ä–Ľ—Ź–Ĺ–ĺ –ł–Ľ–ł —Ä–į–∑–Ī—ä—Ä–ļ–į–Ŗ嬆- –Ĺ—Ź–ľ–į –≤—Ä—ä–∑–ļ–į —Ā —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ĺ—ā–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–į "—Ö–į–ĺ—Ā" –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–ĺ–Ķ—ā–ĺ –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ĺ —Ā –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł—ā–Ķ —Ā–ł—Ā—ā–Ķ–ľ–ł.
–Ę–ĺ–≤–į –∑–≤—É—á–ł –ļ–į—ā–ĺ —Ā—ā—Ä–į–Ĺ–Ķ–Ĺ –≤—ä–Ņ—Ä–ĺ—Ā, –Ķ—ā–ĺ –Ķ–ī–ł–Ĺ –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ķ–Ĺ –Ņ—Ä–ł–ľ–Ķ—Ä. –Ē–į –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á–Ķ –ł–ľ–į —Ā—ā–į—Ź —Ā —ą–Ķ—Ā—ā –ī—É—ą–ł –≤ –Ĺ–Ķ—Ź. –ė–Ĺ—ā–Ķ—Ä–Ķ—Ā—É–≤–į –Ĺ–ł –ī–į–Ľ–ł —Ö–ĺ—Ä–į—ā–į –≤ —ā–į–∑–ł —Ā—ā–į—Ź —Ā–Ķ –Ņ–ĺ–∑–Ĺ–į–≤–į—ā –ł–Ľ–ł –Ĺ–Ķ. –Ě–Ķ–ļ–į –Ĺ–į—Ä–Ķ—á–Ķ–ľ –ī–≤–į–ľ–į –ī—É—ą–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –į–ļ–ĺ —Ā–Ķ –Ņ–ĺ–∑–Ĺ–į–≤–į—ā, –ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł, –į–ļ–ĺ –Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–∑–Ĺ–į–≤–į—ā.
–Ę—ä—Ä—Ā–ł–ľ –Ņ—Ä–ł–ľ–Ķ—Ä–ł –∑–į –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ĺ—Ā—ā –ł –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ –Ĺ–į–Ļ-–Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ł—Ź—ā —Ā–Ľ—É—á–į–Ļ –Ī–ł –Ī–ł–Ľ, –į–ļ–ĺ —ą–Ķ—Ā—ā–ł–ľ–į—ā–į —Ā–į –ł–Ľ–ł –≤—Ā–ł—á–ļ–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –≤—Ā–ł—á–ļ–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –ó–į —Ā—ä–∂–į–Ľ–Ķ–Ĺ–ł–Ķ —Ö–ĺ—Ä–į—ā–į —Ā–į –ł–∑–Ī—Ä–į–Ĺ–ł –Ĺ–į —Ā–Ľ—É—á–į–Ķ–Ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ, —ā–į–ļ–į —á–Ķ –≤ —Ā—ā–į—Ź—ā–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ —Č–Ķ –ł–ľ–į —Ā–ľ–Ķ—Ā–ł—Ü–į –ĺ—ā –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł –ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –Ē–į –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á–Ķ –Ĺ–į—á–Ķ—Ä—ā–į–Ķ–ľ –Ľ–ł–Ĺ–ł–ł, —Ā–≤—ä—Ä–∑–≤–į—Č–ł –≤—Ā—Ź–ļ–į –ī–≤–ĺ–Ļ–ļ–į —Ö–ĺ—Ä–į –≤ —Ā—ā–į—Ź—ā–į, –ł –≥–ł –ĺ—Ü–≤–Ķ—ā–ł–ľ –≤ —Ā–ł–Ĺ—Ć–ĺ, –į–ļ–ĺ –ī–≤–į–ľ–į—ā–į —Ā–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ, –į–ļ–ĺ —Ā–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –Ę–ĺ–≥–į–≤–į —Ä–Ķ–∑—É–Ľ—ā–į—ā—ä—ā –ľ–ĺ–∂–Ķ –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ —Ā–Ľ–Ķ–ī–Ĺ–ł—Ź –Ĺ–į—á–ł–Ĺ:
 |
–Ę–į–∑–ł –ļ–į—Ä—ā–ł–Ĺ–į - –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ —Ź –Ĺ–į—Ä–ł—á–į—ā ‚Äč‚Äč–≥—Ä–į—Ą - –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ĺ–į–Ņ—ä–Ľ–Ĺ–ĺ —Ö–į–ĺ—ā–ł—á–Ĺ–į. –°—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā –Ĺ—Ź–ľ–į–ľ–Ķ —ą–Ķ—Ā—ā–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł –ł–Ľ–ł —ą–Ķ—Ā—ā –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –Ě–ĺ –≤—Ā–Ķ –Ņ–į–ļ –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ–Ņ–ł—ā–į–ľ–Ķ: –ľ–ĺ–∂–Ķ–ľ –Ľ–ł –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –Ņ–ĺ–Ĺ–Ķ —ā—Ä–ł–ľ–į –ī—É—ą–ł –≤ —Ā—ā–į—Ź—ā–į, –ļ–ĺ–ł—ā–ĺ —Ā–į –ł–Ľ–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł? –ö–į–∑–į–Ĺ–ĺ –Ņ–ĺ –ī—Ä—É–≥ –Ĺ–į—á–ł–Ĺ, –ľ–ĺ–∂–Ķ–ľ –Ľ–ł –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ (—ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł) –ł–Ľ–ł —á–Ķ—Ä–≤–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ (—ā—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł)?
–í —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ķ "–ī–į". –ß–į—Ä–Ľ–ł, –ē–≤–Ķ–Ľ–ł–Ĺ –ł –§—Ä–Ķ–ī —Ā–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł –Ķ–ī–ł–Ĺ –∑–į –ī—Ä—É–≥. –Ě–ĺ –ļ–į–ļ–≤–ĺ —Č–Ķ —Ā—ā–į–Ĺ–Ķ, –į–ļ–ĺ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ł—Ź—ā –≥—Ä–į—Ą –Ķ –Ī–ł–Ľ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ? –í–ł–Ĺ–į–≥–ł –Ľ–ł —Č—Ź—Ö–ľ–Ķ –ī–į –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ –Ĺ–į–Ī–ĺ—Ä –ĺ—ā —ā—Ä–ł–ľ–į –ī—É—ą–ł, –ī–į–ī–Ķ–Ĺ–ł –ĺ—ā –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ (–≤—Ā–ł—á–ļ–ł –≤ –Ķ–ī–ł–Ĺ —Ü–≤—Ź—ā, –ĺ—ā –≥—Ä—ä—Ü–ļ–ł monos, ‚Äě–Ķ–ī–ł–Ĺ–ł—á–Ķ–Ĺ‚Äú, –ł chroma , ‚Äě—Ü–≤—Ź—ā‚Äú)?
–ē–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–ł—Ä–į–Ĺ–Ķ—ā–ĺ —Ā –ľ–į–Ľ–ļ–ĺ —Ö–į—Ä—ā–ł—Ź –ł —Ü–≤–Ķ—ā–Ĺ–ł –ľ–ĺ–Ľ–ł–≤–ł —Ā–ļ–ĺ—Ä–ĺ —Č–Ķ –≤–ł —É–Ī–Ķ–ī–ł, —á–Ķ —Ā —ą–Ķ—Ā—ā –ī—É—ą–ł –≤–ł–Ĺ–į–≥–ł –ł–ľ–į –Ķ–ī–Ĺ–ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ. –Ě–ĺ –ļ–į–ļ –ī–į –ī–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ —ā–ĺ–≤–į –Ķ –≤—Ź—Ä–Ĺ–ĺ? –ē–ī–ł–Ĺ –ĺ—ā –Ĺ–į—á–ł–Ĺ–ł—ā–Ķ –Ī–ł –Ī–ł–Ľ –Ņ—Ä–ĺ—Ā—ā–ĺ –ī–į –ł–∑–Ī—Ä–ĺ–ł–ľ –≤—Ā–ł—á–ļ–ł –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–ł—Ź –ł –ī–į –Ņ—Ä–ĺ–≤–Ķ—Ä–ł–ľ –≤—Ā–Ķ–ļ–ł –ĺ—ā —ā—Ź—Ö. –ó–į —Ā—ä–∂–į–Ľ–Ķ–Ĺ–ł–Ķ –ł–ľ–į –Ĺ–į–ī 30 000 –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–ł—Ź, —ā–į–ļ–į —á–Ķ —ā–ĺ–≤–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ī–ł –Ī–ł–Ľ–ĺ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā –ī–ĺ—Ā–į–ī–Ĺ–ĺ.
–ó–į —Č–į—Ā—ā–ł–Ķ —Ā–Ķ –ĺ–ļ–į–∑–≤–į, —á–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –≥–ĺ –ī–ĺ–ļ–į–∂–Ķ–ľ –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–Ľ–Ķ—Ā–Ĺ–ĺ. –ü—ä—Ä–≤–ĺ –ł–∑–Ī–ł—Ä–į–ľ–Ķ –ļ–ĺ—Ź—ā–ĺ –ł –ī–į –Ķ —ā–ĺ—á–ļ–į, –ĺ—ā –Ĺ–Ķ—Ź –ł–∑–Ľ–ł–∑–į—ā –Ņ–Ķ—ā –Ľ–ł–Ĺ–ł–ł - –Ņ–ĺ –Ķ–ī–Ĺ–į –ļ—ä–ľ –≤—Ā—Ź–ļ–į –ĺ—ā –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ –Ņ–Ķ—ā —ā–ĺ—á–ļ–ł:
 |
–ü—Ä–ł –Ņ–Ķ—ā –Ľ–ł–Ĺ–ł–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ņ–ĺ–Ĺ–Ķ —ā—Ä–ł –ĺ—ā –Ķ–ī–ł–Ĺ —Ü–≤—Ź—ā - –Ņ–ĺ–Ĺ–Ķ —ā—Ä–ł —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł –ł–Ľ–ł –Ņ–ĺ–Ĺ–Ķ —ā—Ä–ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł. –Ē–į –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á–Ķ –ł–ľ–į —ā—Ä–ł —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł (–į–ļ–ĺ –≤–ľ–Ķ—Ā—ā–ĺ —ā—Ź—Ö –ł–ľ–į—ą–Ķ —ā—Ä–ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –į—Ä–≥—É–ľ–Ķ–Ĺ—ā—ä—ā —Č–Ķ—ą–Ķ –ī–į –Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ —Ā—ä—Č–ł—Ź—ā, –Ĺ–ĺ —Ā —Ä–į–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł ‚Äě—á–Ķ—Ä–≤–Ķ–Ĺ–ĺ‚Äú –ł ‚Äě—Ā–ł–Ĺ—Ć–ĺ‚Äú). –Ę–į–ļ–į —á–Ķ –ł–ľ–į–ľ–Ķ —á–Ķ—ā–ł—Ä–ł —ā–ĺ—á–ļ–ł –ļ–į—ā–ĺ —ā–į–∑–ł:
 |
–ö–į–ļ–≤–ł —Ā–į —Ü–≤–Ķ—ā–ĺ–≤–Ķ—ā–Ķ –Ĺ–į –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ —ā—Ä–ł –Ľ–ł–Ĺ–ł–ł? –ē, –į–ļ–ĺ –ī–ĺ—Ä–ł –Ķ–ī–ł–Ĺ –ĺ—ā —ā—Ź—Ö –Ķ —á–Ķ—Ä–≤–Ķ–Ĺ, —ā–ĺ–≥–į–≤–į —ā–ĺ–Ļ –Ņ—Ä–į–≤–ł —á–Ķ—Ä–≤–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –∑–į–Ķ–ī–Ĺ–ĺ —Ā —ā–ĺ—á–ļ–į –ź (–≤–Ľ—Ź–≤–ĺ). –ė –į–ļ–ĺ –Ĺ–Ķ, —ā—Ä–ł—ā–Ķ –∑–į–Ķ–ī–Ĺ–ĺ –Ņ—Ä–į–≤—Ź—ā —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ (–≤–ī—Ź—Ā–Ĺ–ĺ):
 |
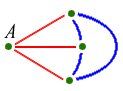 |
–Ę–į–ļ–į –ł–Ľ–ł –ł–Ĺ–į—á–Ķ –ł–ľ–į–ľ–Ķ –Ĺ–į—ą–ł—Ź –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ.
–Ē–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł –Ľ–ł —Ā–į 5 —ā–ĺ—á–ļ–ł?
–Ē–ĺ–ļ–į–∑–į—Ö–ľ–Ķ, —á–Ķ –Ņ—Ä–ł —ą–Ķ—Ā—ā —ā–ĺ—á–ļ–ł (–ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ), –≤–ł–Ĺ–į–≥–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ķ–ī–Ĺ–ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ - —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł, —á–Ķ –Ņ—Ä–ł —ą–Ķ—Ā—ā –ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ –ī—É—ą–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł.
–Ę–ĺ–≤–į –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į –≤—ä–Ņ—Ä–ĺ—Ā–į ‚Äě–ö–ĺ–Ľ–ļ–ĺ –ī—É—ą–ł –Ĺ–ł —ā—Ä—Ź–Ī–≤–į—ā, –∑–į –ī–į —Ā–ľ–Ķ —Ā–ł–≥—É—Ä–Ĺ–ł, —á–Ķ —Č–Ķ –Ĺ–į–ľ–Ķ—Ä–ł–ľ –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł?‚Äú –Ę–ĺ–≤–į –Ķ –Ņ—ä—Ä–≤–ł—Ź—ā –Ĺ–ł –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į —á–ł—Ā–Ľ–ĺ –Ĺ–į –†–į–ľ–∑–ł –ł —Ā–Ķ –∑–į–Ņ–ł—Ā–≤–į –ļ–į—ā–ĺ R (3,3). –í–ł–ī—Ź—Ö–ľ–Ķ, —á–Ķ —ą–Ķ—Ā—ā–ł–ľ–į –ī—É—ą–ł —Ā—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł. –° –ī—Ä—É–≥–ł –ī—É–ľ–ł, R (3,3) –Ĺ–Ķ –Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–ĺ –ĺ—ā 6. –Ě–ĺ –ī–į–Ľ–ł –Ņ–Ķ—ā —ā–ĺ—á–ļ–ł –Ī–ł—Ö–į –Ī–ł–Ľ–ł –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł - —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł, —ā–į–ļ–į –Ľ–ł –Ķ, —á–Ķ –≤—Ā—Ź–ļ–į –≥—Ä—É–Ņ–į –ĺ—ā –Ņ–Ķ—ā–ł–ľ–į –ī—É—ą–ł —Č–Ķ –ł–ľ–į –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł? –ď—Ä–į—Ą—ä—ā –Ņ–ĺ-–ī–ĺ–Ľ—É —Ā –Ņ–Ķ—ā —ā–ĺ—á–ļ–ł –Ņ–ĺ–ļ–į–∑–≤–į, —á–Ķ –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ķ –Ĺ–Ķ, —ā—ä–Ļ –ļ–į—ā–ĺ –Ĺ—Ź–ľ–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ:
 |
–Ę–ĺ–≤–į –Ņ–ĺ–ļ–į–∑–≤–į, —á–Ķ R(3,3) –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā 6. –ź–ļ–ĺ –≤–∑–Ķ–ľ–Ķ–ľ —ā–Ķ–∑–ł –ī–≤–į —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –∑–į–Ķ–ī–Ĺ–ĺ, –ī–ĺ–ļ–į–∑–≤–į–ľ–Ķ, —á–Ķ R(3,3)=6.
–í —ā—ä—Ä—Ā–Ķ–Ĺ–Ķ –Ĺ–į –Ņ–ĺ–≤–Ķ—á–Ķ —Ä–Ķ–ī
–°–Ķ–≥–į, —Ā–Ľ–Ķ–ī –ļ–į—ā–ĺ —Ä–į–∑–Ī—Ä–į—Ö–ľ–Ķ –ļ–į–ļ–≤–ĺ –Ķ —á–ł—Ā–Ľ–ĺ –Ĺ–į –†–į–ľ–∑–ł, –ľ–ĺ–∂–Ķ–ľ –ī–į —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –ī—Ä—É–≥–ł –Ņ—Ä–ł–ľ–Ķ—Ä–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, R(5,5) —Č–Ķ –Ĺ–ł –ļ–į–∂–Ķ –ļ–ĺ–Ľ–ļ–ĺ –ī—É—ą–ł —Ā–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł, –∑–į –ī–į —Ā–ľ–Ķ —Ā–ł–≥—É—Ä–Ĺ–ł, —á–Ķ —Č–Ķ –Ĺ–į–ľ–Ķ—Ä–ł–ľ –ł–Ľ–ł –Ņ–Ķ—ā–ł–ľ–į –ĺ–Ī—Č–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –Ņ–Ķ—ā–ł–ľ–į –ĺ–Ī—Č–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –†–į–∑–Ī–ł—Ä–į —Ā–Ķ, –≤—Ā–Ķ –ĺ—Č–Ķ –Ĺ–Ķ –∑–Ĺ–į–Ķ–ľ, —á–Ķ –≤–ł–Ĺ–į–≥–ł –ł–ľ–į —ā–į–ļ—ä–≤ –ĺ—ā–≥–ĺ–≤–ĺ—Ä: –ľ–ĺ–∂–Ķ –Ī–ł –Ĺ–ł—ā–ĺ –Ķ–ī–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —Ö–ĺ—Ä–į –Ĺ—Ź–ľ–į –ī–į –≥–į—Ä–į–Ĺ—ā–ł—Ä–į, –ī–į —Ä–Ķ—á–Ķ–ľ, 10 –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł –ł–Ľ–ł 10 –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. (–í—Ā—ä—Č–Ĺ–ĺ—Ā—ā¬†–Ņ–ĺ-–Ĺ–į—ā–į—ā—ä–ļ –≤ —ā–į–∑–ł —Ā—ā–į—ā–ł—Ź —Č–Ķ –ī–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ –≤–ł–Ĺ–į–≥–ł –ł–ľ–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä, –ľ–į–ļ–į—Ä —á–Ķ –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –Ĺ–Ķ –∑–Ĺ–į–Ķ–ľ –ļ–į–ļ—ä–≤ –Ķ —ā–ĺ–Ļ.)
–ó–į –ī–į —Ā–Ķ —É–≤–Ķ—Ä–ł–ľ, —á–Ķ —Ā–ľ–Ķ —Ä–į–∑–Ī—Ä–į–Ľ–ł –ī–ĺ—ā—É–ļ, –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ –ī–≤–į –≤—ä–Ņ—Ä–ĺ—Ā–į:
- –ö–į–ļ–≤–ĺ –Ķ R (2,5)?
- –ź–ļ–ĺ –∑–Ĺ–į–Ķ–ľ R (a, b), –ļ–į–ļ–≤–ĺ –ľ–ĺ–∂–Ķ–ľ –ī–į –ļ–į–∂–Ķ–ľ –∑–į R (b, a)?
–ē—ā–ĺ —Ä–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź—ā–į:
1. –ß–ł—Ā–Ľ–ĺ—ā–ĺ –Ĺ–į –†–į–ľ–∑–ł R(2,5)
–Ę–ĺ–≤–į –Ķ —á–ł—Ā–Ľ–ĺ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ —Č–Ķ –ĺ—ā–≥–ĺ–≤–ĺ—Ä–ł –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā–į: "–ö–ĺ–Ľ–ļ–ĺ –ī—É—ą–ł —Ā–į –Ĺ–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł, –∑–į –ī–į —Ā–ľ–Ķ —Ā–ł–≥—É—Ä–Ĺ–ł, —á–Ķ —Č–Ķ –ł–ľ–į–ľ–Ķ –ł–Ľ–ł –ī–≤–į–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –Ņ–Ķ—ā–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł?"
–Ě–ĺ, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ, –į–ļ–ĺ –≤ —Ā—ā–į—Ź—ā–į –ł–ľ–į –Ĺ—Ź–ļ–į–ļ–≤–ł –ī–≤–į–ľ–į –ī—É—ą–ł, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –Ņ–ĺ–∑–Ĺ–į–≤–į—ā, —ā–ĺ–≤–į –Ĺ–ł –ī–į–≤–į –Ĺ–į—ą–ł—ā–Ķ –ī–≤–į–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł. –ě—ā –ī—Ä—É–≥–į —Ā—ā—Ä–į–Ĺ–į, –į–ļ–ĺ –Ĺ–Ķ —Ā–į, —ā–ĺ–≥–į–≤–į –≤—Ā–ł—á–ļ–ł —Ö–ĺ—Ä–į –≤ —Ā—ā–į—Ź—ā–į —Ā–į –≤–∑–į–ł–ľ–Ĺ–ĺ –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –Ę–į–ļ–į —á–Ķ —Č–ĺ–ľ –ł–ľ–į –Ņ–Ķ—ā–ł–ľ–į –ī—É—ą–ł, —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –ł–Ľ–ł –ī–≤–į–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –Ņ–Ķ—ā–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł.
–Ě–į–ļ—Ä–į—ā–ļ–ĺ, R(2,5)=5. –†–į–∑–Ī–ł—Ä–į —Ā–Ķ, —Ā—ä—Č–ĺ—ā–ĺ —Ä–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł–Ķ –Ī–ł —Ä–į–Ī–ĺ—ā–ł–Ľ–ĺ –ł —Ā –ī—Ä—É–≥–ĺ —á–ł—Ā–Ľ–ĺ –≤–ľ–Ķ—Ā—ā–ĺ 5, —ā–į–ļ–į —á–Ķ –Ņ–ĺ-–ĺ–Ī—Č–ĺ –ľ–ĺ–∂–Ķ–ľ –ī–į –ļ–į–∂–Ķ–ľ, —á–Ķ R(2,a)=a, –∑–į –≤—Ā—Ź–ļ–ĺ —á–ł—Ā–Ľ–ĺ a.
2.–í—Ä—ä–∑–ļ–į—ā–į –ľ–Ķ–∂–ī—É R(a,b) –ł R(b,a)
–ě—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į –Ĺ—Ź–ľ–į –Ĺ–ł—Č–ĺ —Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ –≤ –ī—É–ľ–ł—ā–Ķ "–Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł" –ł–Ľ–ł "–Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł" - –ł–Ľ–ł, –Ņ–ĺ–≥–Ľ–Ķ–ī–Ĺ–į—ā–ĺ –Ņ–ĺ –ī—Ä—É–≥ –Ĺ–į—á–ł–Ĺ, –≤ —Ü–≤–Ķ—ā–ĺ–≤–Ķ—ā–Ķ "—Ā–ł–Ĺ—Ć–ĺ" –ł "—á–Ķ—Ä–≤–Ķ–Ĺ–ĺ". –ö–ĺ–≥–į—ā–ĺ –ł–ľ–į—ā–Ķ –≥—Ä–į—Ą —Ā—ä—Ā —Ā–ł–Ĺ–ł –ł —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –ľ–ĺ–∂–Ķ—ā–Ķ –ī–į –≥–ł —Ä–į–∑–ľ–Ķ–Ĺ–ł—ā–Ķ, —ā–į–ļ–į —á–Ķ —á–Ķ—Ä–≤–Ķ–Ĺ–ł—ā–Ķ –ī–į —Ā—ā–į–Ĺ–į—ā —Ā–ł–Ĺ–ł –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ, –į–ļ–ĺ –Ķ–ī–Ĺ–į –≥—Ä—É–Ņ–į –ĺ—ā —Ö–ĺ—Ä–į –Ķ –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ–į, –∑–į –ī–į —Ā—ä–ī—ä—Ä–∂–į –ł–Ľ–ł a –ĺ–Ī—Č–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł b –ĺ–Ī—Č–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł, —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ —Ā—ä—Č–ĺ —ā–ĺ–Ľ–ļ–ĺ–≤–į –≤—Ź—Ä–Ĺ–ĺ, —á–Ķ —ā—Ź —Ā—ä–ī—ä—Ä–∂–į –ł–Ľ–ł a –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł, –ł–Ľ–ł b –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł. –° –ī—Ä—É–≥–ł –ī—É–ľ–ł, R(a,b)=R(b,a). –ú–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –Ī–ł –ļ–į–∑–į–Ľ, —á–Ķ —Ą—É–Ĺ–ļ—Ü–ł—Ź—ā–į R –Ķ —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–į.
–°–Ķ–≥–į –Ĺ–Ķ–ļ–į –Ī—ä–ī–Ķ–ľ –Ņ–ĺ-–į–ľ–Ī–ł—Ü–ł–ĺ–∑–Ĺ–ł: –ł—Ā–ļ–į–ľ–Ķ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ —á–Ķ—ā–ł—Ä–ł–ľ–į –ī—É—ą–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į –ł–Ľ–ł –≤—Ā–ł—á–ļ–ł –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł –≤—Ā–ł—á–ļ–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –ė—Ā–ļ–į–ľ–Ķ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ R(4,4). –ó–į –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –ĺ–Ī–į—á–Ķ —ā–ĺ–≤–į –Ķ —ā–≤—ä—Ä–ī–Ķ —ā—Ä—É–ī–Ĺ–ĺ, –∑–į—ā–ĺ–≤–į —Č–Ķ —Ā–Ķ –∑–į–ī–ĺ–≤–ĺ–Ľ–ł–ľ —Ā –Ĺ–Ķ—Č–ĺ –ľ–į–Ľ–ļ–ĺ –Ņ–ĺ-–Ľ–Ķ—Ā–Ĺ–ĺ, –į –ł–ľ–Ķ–Ĺ–Ĺ–ĺ –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į R(3,4).
–Ě–į–ľ–ł—Ä–į–Ĺ–Ķ –Ĺ–į R (3,4)
–ö–ĺ–Ľ–ļ–ĺ —ā–ĺ—á–ļ–ł —Ā–į –Ĺ–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł, –∑–į –ī–į –≥–į—Ä–į–Ĺ—ā–ł—Ä–į–ľ–Ķ, —á–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –ł–Ľ–ł —ā—Ä–ł —ā–ĺ—á–ļ–ł, –≤—Ā–ł—á–ļ–ł —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā—ä—Ā —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł —ā–ĺ—á–ļ–ł, –≤—Ā–ł—á–ļ–ł —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł - —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł, –Ķ–ī–Ĺ–ĺ –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ?
 |
 |
–ü—ä—Ä–≤–ĺ, —ā–≤—ä—Ä–ī–ł–ľ, —á–Ķ 10 —ā–ĺ—á–ļ–ł —Ā—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł. –Ě–Ķ–ļ–į —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –ī–ĺ–ļ–į–∂–Ķ–ľ —ā–ĺ–≤–į. –Ē–į –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ, —á–Ķ –ł–ľ–į–ľ–Ķ 10 —ā–ĺ—á–ļ–ł, —Ā—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł —Ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł –Ņ–ĺ –ĺ–Ī–ł—á–į–Ļ–Ĺ–ł—Ź –Ĺ–į—á–ł–Ĺ. –ė–∑–Ī–Ķ—Ä–Ķ—ā–Ķ —ā–ĺ—á–ļ–į –ł –∑–į–Ī–Ķ–Ľ–Ķ–∂–Ķ—ā–Ķ, —á–Ķ –ĺ—ā –Ĺ–Ķ—Ź –ł–∑–Ľ–ł–∑–į—ā 9 –Ľ–ł–Ĺ–ł–ł.
 |
–Ę—Ä—Ź–Ī–≤–į –ł–Ľ–ł –ī–į –ł–ľ–į –Ņ–ĺ–Ĺ–Ķ 6 —á–Ķ—Ä–≤–Ķ–Ĺ–ł, –ł–Ľ–ł –Ņ–ĺ–Ĺ–Ķ 4 —Ā–ł–Ĺ–ł (–≤ –Ņ—Ä–ĺ—ā–ł–≤–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ –Ĺ—Ź–ľ–į –ī–į –ł–ľ–į –ĺ–Ī—Č–ĺ 10) –Ę–į–ļ–į —á–Ķ —Ā–ľ–Ķ –≤ –Ķ–ī–Ĺ–į –ĺ—ā —ā–Ķ–∑–ł –ī–≤–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł (–Ĺ–į—á–Ķ—Ä—ā–į–Ĺ–ł —Ā–į —Ā–į–ľ–ĺ –Ľ–ł–Ĺ–ł–ł—ā–Ķ, –ļ–ĺ–ł—ā–ĺ –Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā—É–≤–į—ā ):
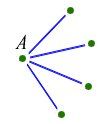
–°–Ľ—É—á–į–Ļ (i) |
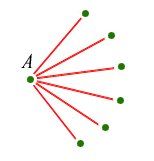
–°–Ľ—É—á–į–Ļ (ii) |
–Ě–Ķ–ļ–į –Ņ—ä—Ä–≤–ĺ —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ —Ā–Ľ—É—á–į–Ļ (i). –ö–į–ļ—ä–≤ —Ü–≤—Ź—ā —Ā–į –Ľ–ł–Ĺ–ł–ł—ā–Ķ –≤ (i), —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ĺ—ā –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł—ā–Ķ —Ā–ł–Ĺ–ł? –ź–ļ–ĺ –ī–ĺ—Ä–ł –Ķ–ī–ł–Ĺ –ĺ—ā —ā—Ź—Ö –Ķ —Ā–ł–Ĺ, –ł–ľ–į–ľ–Ķ —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł (–≤–Ľ—Ź–≤–ĺ); –į–ļ–ĺ –Ĺ–Ķ, –≤—Ā–ł—á–ļ–ł —Ā–į —á–Ķ—Ä–≤–Ķ–Ĺ–ł –ł –ł–ľ–į–ľ–Ķ —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł (–≤–ī—Ź—Ā–Ĺ–ĺ). –ė –≤ –ī–≤–į—ā–į —Ā–Ľ—É—á–į—Ź —Ā–ľ–Ķ –≥–ĺ—ā–ĺ–≤–ł:
 |
 |
–°–Ķ–≥–į –Ĺ–Ķ–ļ–į –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ —Ā–Ľ—É—á–į–Ļ (ii). –Ę–į–ľ –ł–ľ–į 6 —ā–ĺ—á–ļ–ł (–ĺ—Ā–≤–Ķ–Ĺ –ź). –ė –≤–Ķ—á–Ķ –ĺ—ā–ļ—Ä–ł—Ö–ľ–Ķ, —á–Ķ R (3,3)=6, —ā–į–ļ–į —á–Ķ –ĺ—ā —ā–Ķ–∑–ł 6 —ā–ĺ—á–ļ–ł 3 —ā—Ä—Ź–Ī–≤–į –ī–į –ĺ–Ī—Ä–į–∑—É–≤–į—ā –ł–Ľ–ł —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –ł–Ľ–ł —á–Ķ—Ä–≤–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –ļ–ĺ–Ķ—ā–ĺ –Ĺ–ł –Ņ–ĺ—Ā—ā–į–≤—Ź –≤ –Ķ–ī–ł–Ĺ –ĺ—ā —ā–Ķ–∑–ł –ī–≤–į —Ā–Ľ—É—á–į—Ź:
 |
 |
–í —Ā–Ľ—É—á–į—Ź –ĺ—ā–Ľ—Ź–≤–ĺ –ł–ľ–į–ľ–Ķ —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –į –≤ —Ā–Ľ—É—á–į—Ź –ĺ—ā–ī—Ź—Ā–Ĺ–ĺ —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –Ę–į–ļ–į —á–Ķ –ĺ—Č–Ķ –≤–Ķ–ī–Ĺ—ä–∂ —Ā–ľ–Ķ –≥–ĺ—ā–ĺ–≤–ł.
–Ę–ĺ–∑–ł –į—Ä–≥—É–ľ–Ķ–Ĺ—ā –Ķ –Ņ–ĺ—Ā—ā–į–≤–ł–Ľ –≥—Ä–į–Ĺ–ł—Ü–į –Ĺ–į R (3,4): –∑–Ĺ–į–Ķ–ľ, —á–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 10. –Ě–ĺ –≤—Ā–Ķ –Ņ–į–ļ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā 10. –í—Ā—ä—Č–Ĺ–ĺ—Ā—ā, —á—Ä–Ķ–∑ –Ķ–ī–Ĺ–į –≤–į—Ä–ł–į—Ü–ł—Ź –Ĺ–į –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į –Ņ–ĺ-–≥–ĺ—Ä–Ķ, –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ —á–Ķ 9 —ā–ĺ—á–ļ–ł —Č–Ķ —Ā–≤—ä—Ä—ą–į—ā —Ä–į–Ī–ĺ—ā–į.
–Ē–Ķ–≤–Ķ—ā —ā–ĺ—á–ļ–ł —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł
–ó–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ –ī–ĺ—Ä–ł –Ņ—Ä–ł —Ā–į–ľ–ĺ –ī–Ķ–≤–Ķ—ā —ā–ĺ—á–ļ–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –ł–Ľ–ł —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł —ā–ĺ—á–ļ–ł, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, —Ā–Ķ –Ĺ—É–∂–ī–į–Ķ–ľ –ĺ—ā –Ľ–Ķ–ļ–ĺ –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ–Ĺ–ł–Ķ –Ĺ–į —Ä–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź—ā–į, –ļ–ĺ–ł—ā–ĺ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—Ö–ľ–Ķ –∑–į 10 —ā–ĺ—á–ļ–ł.
–ü—Ä–ł 10 —ā–ĺ—á–ļ–ł –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ —Ā–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–≤–į—ą–Ķ –Ĺ–į –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–ĺ—á–ļ–į, —Ā–≤—ä—Ä–∑–į–Ĺ–į –ł–Ľ–ł —Ā –Ņ–ĺ–Ĺ–Ķ —ą–Ķ—Ā—ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –ł–Ľ–ł —Ā –Ņ–ĺ–Ĺ–Ķ —á–Ķ—ā–ł—Ä–ł —Ā–ł–Ĺ–ł. –°–Ľ–Ķ–ī –ļ–į—ā–ĺ —Ä–į–∑–Ņ–ĺ–Ľ–į–≥–į—Ö–ľ–Ķ —Ā —ā–į–ļ–į–≤–į —ā–ĺ—á–ļ–į, –ľ–ĺ–∂–Ķ—Ö–ľ–Ķ –ī–į —Ā–ľ–Ķ —Ā–ł–≥—É—Ä–Ĺ–ł, —á–Ķ —Č–Ķ –Ĺ–į–ľ–Ķ—Ä–ł–ľ –Ĺ–į—ą–ł—ā–Ķ —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –ė –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā, –ļ–į—ā–ĺ –Ņ—Ä–Ķ–Ī—Ä–ĺ–ł—Ö–ľ–Ķ –Ľ–ł–Ĺ–ł–ł—ā–Ķ, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ —Ā—Ä–Ķ—Č–į—ā –≤ –ī–į–ī–Ķ–Ĺ–į —ā–ĺ—á–ļ–į, –≤–ł–ī—Ź—Ö–ľ–Ķ, —á–Ķ –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –Ķ –Ņ–ĺ–ī—Ö–ĺ–ī—Ź—Č–į.
–ź–ļ–ĺ –≥—Ä–į—Ą—ä—ā –ł–ľ–į —Ā–į–ľ–ĺ 9 —ā–ĺ—á–ļ–ł, –≤—Ā–Ķ–ļ–ł –ĺ—ā —ā—Ź—Ö –ł–ľ–į —Ā–į–ľ–ĺ 8 —Ā—ä—Ā–Ķ–ī–ł. –ö–į–ļ –ľ–ĺ–∂–Ķ –Ĺ–į—ą–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ī–į —Ā–Ķ –Ņ—Ä–ĺ–≤–į–Ľ–ł? –°–į–ľ–ĺ –į–ļ–ĺ –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ł–ľ–į —ā–ĺ—á–Ĺ–ĺ –Ņ–Ķ—ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł –ł —ā—Ä–ł —Ā–ł–Ĺ–ł. –Ę–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į —ā—Ä—Ź–Ī–≤–į –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ —Ā–Ľ–Ķ–ī–Ĺ–ł—Ź –Ĺ–į—á–ł–Ĺ:
 |
–ö–ĺ–Ľ–ļ–ĺ —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł –Ī–ł –ł–ľ–į–Ľ–į —ā–ĺ–∑–ł –≥—Ä–į—Ą? –ē, –≤—Ā—Ź–ļ–į –Ľ–ł–Ĺ–ł—Ź –ł–ľ–į –ī–≤–į –ļ—Ä–į—Ź, –į –≤—ä–≤ –≤—Ā—Ź–ļ–į –ĺ—ā 9-—ā–Ķ —ā–ĺ—á–ļ–ł —Ā–Ķ —Ā—Ä–Ķ—Č–į—ā –Ņ–ĺ —ā—Ä–ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł. –Ę–į–ļ–į —á–Ķ –ĺ–Ī—Č–ł—Ź—ā –Ī—Ä–ĺ–Ļ –Ĺ–į —Ā–ł–Ĺ–ł—ā–Ķ –Ľ–ł–Ĺ–ł–ł –Ķ (9√ó3)/2, –ļ–ĺ–Ķ—ā–ĺ –Ķ 13,5. –Ę–ĺ–≤–į –Ķ –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ - —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ, —á–Ķ –≤ –≥—Ä–į—Ą–į —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į —Ü—Ź–Ľ –Ī—Ä–ĺ–Ļ —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł.
–Ę–į–ļ–į —á–Ķ –≤ –ļ—Ä–į–Ļ–Ĺ–į —Ā–ľ–Ķ—ā–ļ–į —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ņ–ĺ–Ĺ–Ķ –Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į, —Ā–≤—ä—Ä–∑–į–Ĺ–į –ł–Ľ–ł —Ā —á–Ķ—ā–ł—Ä–ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –ł–Ľ–ł —Ā —ą–Ķ—Ā—ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł, –ł —Ā–Ķ–≥–į —Ā—ä—Č–ł—Ź—ā –į—Ä–≥—É–ľ–Ķ–Ĺ—ā –ļ–į—ā–ĺ –Ņ—Ä–Ķ–ī–ł –Ņ–ĺ–ļ–į–∑–≤–į, —á–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į —ā—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł (—Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ) –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł.
–ě—Ā–Ķ–ľ —ā–ĺ—á–ļ–ł –Ĺ–Ķ —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł
–ě—ā –ī—Ä—É–≥–į —Ā—ā—Ä–į–Ĺ–į, 8 —ā–ĺ—á–ļ–ł –Ĺ—Ź–ľ–į –ī–į —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł, –ļ–į–ļ—ā–ĺ –Ņ–ĺ–ļ–į–∑–≤–į —Ā–Ľ–Ķ–ī–Ĺ–į—ā–į –ī–ł–į–≥—Ä–į–ľ–į. (–í—Ā–ł—á–ļ–ł —Ā–ł–Ĺ–ł –Ľ–ł–Ĺ–ł–ł —Ā–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł; –≤—Ā–ł—á–ļ–ł –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł –Ľ–ł–Ĺ–ł–ł —Ā–Ķ –Ņ—Ä–ł–Ķ–ľ–į—ā –∑–į —á–Ķ—Ä–≤–Ķ–Ĺ–ł.) –Ě–ł–ļ–į–ļ–≤–ł 3 —ā–ĺ—á–ļ–ł –Ĺ–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į—ā —Ā–ł–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł –Ĺ–ł–ļ–į–ļ–≤–ł 4 —ā–ĺ—á–ļ–ł –Ĺ–Ķ —Ā–į —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā —á–Ķ—Ä–≤–Ķ–Ĺ–ł –Ľ–ł–Ĺ–ł–ł.
 |
–°–Ķ–≥–į –∑–Ĺ–į–Ķ–ľ, —á–Ķ R (3,4)=9. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į, –ļ–į–ļ—ā–ĺ –≤–ł–ī—Ź—Ö–ľ–Ķ –Ņ–ĺ-—Ä–į–Ĺ–ĺ, –ľ–ĺ–∂–Ķ–ľ –ī–į —Ä–į–∑–ľ–Ķ–Ĺ–ł–ľ –ľ–Ķ—Ā—ā–į—ā–į –Ĺ–į "—á–Ķ—Ä–≤–Ķ–Ĺ–ĺ" –ł "—Ā–ł–Ĺ—Ć–ĺ", —ā–į–ļ–į —á–Ķ —Ā—ä—Č–ł—Ź—ā –į—Ä–≥—É–ľ–Ķ–Ĺ—ā –Ņ–ĺ–ļ–į–∑–≤–į, —á–Ķ R (4,3)=9.
–Ě–į–ľ–ł—Ä–į–Ĺ–Ķ –Ĺ–į R (4,4)
–°–Ķ–≥–į –ľ–ĺ–∂–Ķ–ľ –ī–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–ľ–Ķ —ā–ĺ–≤–į –∑–Ĺ–į–Ĺ–ł–Ķ, –∑–į –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ R (4,4). –ü—ä—Ä–≤–ĺ, —ā–≤—ä—Ä–ī–ł–ľ, —á–Ķ 18 –ī—É—ą–ł —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł, –∑–į –ī–į –≥–į—Ä–į–Ĺ—ā–ł—Ä–į–ľ–Ķ –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –ú–Ķ—ā–ĺ–ī—ä—ā –Ĺ–į –ī–ĺ–ļ–į–∑–≤–į–Ĺ–Ķ –≤–Ķ—á–Ķ –Ī–ł —ā—Ä—Ź–Ī–≤–į–Ľ–ĺ –ī–į –∑–į–Ņ–ĺ—á–Ĺ–Ķ –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ–∑–Ĺ–į—ā. –Ē–į –ļ–į–∂–Ķ–ľ, —á–Ķ –ł–ľ–į–ľ–Ķ –≥—Ä–į—Ą —Ā 18 —ā–ĺ—á–ļ–ł –ł –Ľ–ł–Ĺ–ł–ł –ľ–Ķ–∂–ī—É —ā—Ź—Ö, –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –≤ —Ā–ł–Ĺ—Ć–ĺ –ł–Ľ–ł —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ. –Ē–į –≤–∑–Ķ–ľ–Ķ–ľ –Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į. –ě—ā –Ĺ–Ķ—Ź –ł–∑–Ľ–ł–∑–į—ā 17 —Ä–Ķ–Ī—Ä–į, —ā–į–ļ–į —á–Ķ –Ņ–ĺ–Ĺ–Ķ 9 –ĺ—ā —ā—Ź—Ö —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–į –Ķ–ī–Ĺ–ĺ—Ü–≤–Ķ—ā–Ĺ–ł - —á–Ķ—Ä–≤–Ķ–Ĺ–ł, –ī–į —Ä–Ķ—á–Ķ–ľ:
 |
–í–Ķ—á–Ķ –∑–Ĺ–į–Ķ–ľ, —á–Ķ R (4,3)=9, —ā–į–ļ–į —á–Ķ —Ā—Ä–Ķ–ī —ā–Ķ–∑–ł 9 —ā–ĺ—á–ļ–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł - –≤ –ļ–ĺ–Ļ—ā–ĺ —Ā–Ľ—É—á–į–Ļ —Ā–ľ–Ķ –≥–ĺ—ā–ĺ–≤–ł - –ł–Ľ–ł —ā—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł. –í –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ, —ā—ä–Ļ –ļ–į—ā–ĺ –ł —ā—Ä–ł—ā–Ķ —Ā–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł –∑–į A , –ł–ľ–į–ľ–Ķ —á–Ķ—ā–ł—Ä–ł –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ A. –Ę–į–ļ–į —á–Ķ –ł–ľ–į–ľ–Ķ –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ņ—Ä–ł—Ź—ā–Ķ–Ľ–ł, –ł–Ľ–ł —á–Ķ—ā–ł—Ä–ł–ľ–į –Ĺ–Ķ–Ņ–ĺ–∑–Ĺ–į—ā–ł, –ļ–ĺ–Ķ—ā–ĺ –Ķ —ā–ĺ—á–Ĺ–ĺ —ā–ĺ–≤–į, –ļ–ĺ–Ķ—ā–ĺ —ā–≤—ä—Ä–ī–Ķ—Ö–ľ–Ķ.
–ě—Č–Ķ –≤–Ķ–ī–Ĺ—ä–∂ –ĺ—ā–ļ—Ä–ł—Ö–ľ–Ķ –≥—Ä–į–Ĺ–ł—Ü–į: R (4,4) —Ā—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ł –Ķ –Ĺ–į–Ļ-–ľ–Ĺ–ĺ–≥–ĺ 18. –Ę–ĺ–∑–ł –Ņ—ä—ā, –∑–į –ļ—ä—Ā–ľ–Ķ—ā, –≥—Ä–į–Ĺ–ł—Ü–į—ā–į —Ā–Ķ –ĺ–ļ–į–∑–≤–į –Ĺ–į–Ļ-–ī–ĺ–Ī—Ä–į—ā–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–į: 17 —ā–ĺ—á–ļ–ł –Ĺ–Ķ —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł, –∑–į –ī–į –≥–į—Ä–į–Ĺ—ā–ł—Ä–į—ā –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ –Ĺ–į–Ī–ĺ—Ä –ĺ—ā —á–Ķ—ā–ł—Ä–ł —ā–ĺ—á–ļ–ł. –ó–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ —ā–ĺ–≤–į, —ā—Ä—Ź–Ī–≤–į –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –≥—Ä–į—Ą —Ā—ä—Ā 17 —ā–ĺ—á–ļ–ł –Ī–Ķ–∑ —ā–į–ļ—ä–≤ –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ –Ĺ–į–Ī–ĺ—Ä. –Ę–ĺ–≤–į –Ķ –Ĺ–į–Ņ—Ä–į–≤–Ķ–Ĺ–ĺ –ł –ľ–ĺ–∂–Ķ –ī–į go –≤–ł–ī–ł—ā–Ķ –Ĺ–į –ĺ—ā–ī–Ķ–Ľ–Ĺ–į —Ā—ā—Ä–į–Ĺ–ł—Ü–į.¬†
–í —Ä–Ķ–∑—É–Ľ—ā–į—ā –∑–Ĺ–į–Ķ–ľ, —á–Ķ R (4,4)=18.
–ü–ĺ-–≥–ĺ–Ľ–Ķ–ľ–ł —á–ł—Ā–Ľ–į –Ĺ–į –†–į–ľ–∑–ł
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–į—ā–į —Ā—ā—ä–Ņ–ļ–į –Ņ–ĺ–ļ–į–∑–į, —á–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ—Ā—ā–į–≤–ł–ľ –≥—Ä–į–Ĺ–ł—Ü–į –Ĺ–į R (4,4), —Ā—ā–ł–≥–į –ī–į –ł–ľ–į–ľ–Ķ –≥—Ä–į–Ĺ–ł—Ü–ł –∑–į R (3,4) –ł R (4,3). –Ę–Ķ —Ā—ä—Č–ĺ —Ā–Ķ —Ä–į–∑–ī–Ķ–Ľ—Ź—ā –Ĺ–į –Ņ–ĺ-–Ņ—Ä–ĺ—Ā—ā–ł —Ā—ā—ä–Ņ–ļ–ł: –ľ–ĺ–∂–Ķ–ľ –ī–į –ĺ–Ī–≤—ä—Ä–∂–Ķ–ľ R (3,4), —Ā—ā–ł–≥–į –ī–į –ľ–ĺ–∂–Ķ–ľ –ī–į –ĺ–Ī–≤—ä—Ä–∂–Ķ–ľ R (3,3) –ł R (2,4) –ł —ā.–Ĺ.¬†M–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ļ–į–∑–į–Ĺ–ĺ R (a, b)¬†—Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į, —Ā—ā–ł–≥–į –ī–į —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā R (a-1, b) –ł R (a, b-1).
–°—ä—Č–ĺ —ā–į–ļ–į –≤–Ķ—á–Ķ –≤–ł–ī—Ź—Ö–ľ–Ķ, —á–Ķ R (a ,2) –ł R (2, a) –≤–ł–Ĺ–į–≥–ł —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā (—ā–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ —Ā–į —Ä–į–≤–Ĺ–ł –Ĺ–į a). –Ę–į–ļ–į —á–Ķ, –∑–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä R (5,5) —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į, —Č–Ķ —Ā–Ķ —Ä–į–∑–ī–Ķ–Ľ–ł–ľ –Ĺ–į –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į –ĺ—ā —Ā—ā—ä–Ņ–ļ–ł, –ļ–į–ļ—ā–ĺ –Ķ –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į:
 |
–í—Ā–Ķ–ļ–ł —Ā–Ľ—É—á–į–Ļ —Ā–Ķ —Ä–į–∑–ī–Ķ–Ľ—Ź –Ĺ–į –ī–≤–į—ā–į —Ā–Ľ—É—á–į—Ź –Ņ–ĺ–ī –Ĺ–Ķ–≥–ĺ –ł –Ĺ–ł–Ķ –≤–Ķ—á–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł—Ö–ľ–Ķ —Ā–Ľ—É—á–į–ł—ā–Ķ –≤ –ī–ĺ–Ľ–Ĺ–ł—Ź —Ä–Ķ–ī. –Ę–į–ļ–į —á–Ķ R (5,5) —Ā—ä—Ā —Ā–ł–≥—É—Ä–Ĺ–ĺ—Ā—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ł –Ņ–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –∑–į R (6,6) –ł–Ľ–ł –≤—Ā—Ź–ļ–ĺ R (a,b). –Ę–ĺ–≤–į –Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ĺ–į –†–į–ľ–∑–ł –ł —ā—Ź –Ĺ–ł –ļ–į–∑–≤–į, —á–Ķ¬†–≤–ł–Ĺ–į–≥–ł –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ĺ—Ā—ā, —Ā—ā–ł–≥–į –ī–į–ī–Ķ–Ĺ–ł—Ź—ā –≥—Ä–į—Ą—ä—ā –ī–į –Ķ –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ.
–í–į–∂–Ĺ–ĺ –Ķ –ĺ–Ī–į—á–Ķ –ī–į —Ā–Ķ –∑–į–Ņ–ĺ–ľ–Ĺ–ł–Ķ, —á–Ķ —ā–ĺ–∑–ł –ľ–Ķ—ā–ĺ–ī –Ĺ–Ķ –Ĺ–į–ľ–ł—Ä–į —ā–ĺ—á–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ĺ–į –†–į–ľ–∑–ł –≤–ľ–Ķ—Ā—ā–ĺ –Ĺ–į—Ā, –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –Ĺ–ł –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į –ī–į –Ĺ–į–ľ–ł—Ä–į–ľ–Ķ –≥—Ä–į–Ĺ–ł—Ü–ł.
–Ě–ł–ļ–ĺ–Ļ –Ĺ–Ķ –∑–Ĺ–į–Ķ
–ė —ā–į–ļ–į, –ļ–į–ļ–≤–į –Ķ –ł—Ā—ā–ł–Ĺ—Ā–ļ–į—ā–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā –Ĺ–į R (5,5)?
–ě—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ķ: –Ĺ–ł–ļ–ĺ–Ļ –Ĺ–Ķ –∑–Ĺ–į–Ķ!
–í—Ā—ä—Č–Ĺ–ĺ—Ā—ā –ľ–Ĺ–ĺ–≥–ĺ –ľ–į–Ľ–ļ–ĺ —á–ł—Ā–Ľ–į –Ĺ–į –†–į–ľ–∑–ł R (a, b) —Ā–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł (–ļ–į—ā–ĺ a –ł b —Ā–į –Ņ–ĺ-–≥–ĺ–Ľ–Ķ–ľ–ł –ĺ—ā 2). –í–Ķ—á–Ķ –≤–ł–ī—Ź—Ö–ľ–Ķ, —á–Ķ R (3,3)=6, R (4,3)=9 –ł R (4,4)=18. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į —Ā–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł —Ā–į–ľ–ĺ –ĺ—Č–Ķ —ā—Ä–ł —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł: R (5,3)=14, R (6,3)=18 –ł R (7,3)=23. –Ě–į–Ļ-–ľ–Ĺ–ĺ–≥–ĺ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ–ľ –ī–į –ļ–į–∂–Ķ–ľ –∑–į R (5,5) —Ā –Ĺ–į—Ā—ā–ĺ—Ź—Č–ł—ā–Ķ –Ĺ–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź –Ķ, —á–Ķ –Ķ –Ĺ—Ź–ļ—ä–ī–Ķ –ľ–Ķ–∂–ī—É 42 –ł 55.
–ó–į—Ȗ嬆–Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į —ā—Ä—É–ī–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–ł —ā–ĺ—á–Ĺ–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā? –ź—Ä–≥—É–ľ–Ķ–Ĺ—ā–ł –ļ–į—ā–ĺ —ā–Ķ–∑–ł, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–ł –≤ —ā–į–∑–ł —Ā—ā–į—ā–ł—Ź, –Ĺ–ł –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į—ā –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –≥–ĺ—Ä–Ĺ–ł –≥—Ä–į–Ĺ–ł—Ü–ł –Ĺ–į —á–ł—Ā–Ľ–į—ā–į –Ĺ–į –†–į–ľ–∑–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā—É–≤–į—ā - –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤–ł–ī—Ź—Ö–ľ–Ķ –ī–ĺ—Ā—ā–į –Ľ–Ķ—Ā–Ĺ–ĺ, —á–Ķ R (4,3) –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–ĺ –ĺ—ā 10.
–Ě–ĺ –∑–į –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ —ā–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā 8, —ā—Ä—Ź–Ī–≤–į—ą–Ķ –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –ł–∑—Ä–ł—á–Ĺ–ĺ –≥—Ä–į—Ą —Ā 8 —ā–ĺ—á–ļ–ł –ļ–į—ā–ĺ –ļ–ĺ–Ĺ—ā—Ä–į–Ņ—Ä–ł–ľ–Ķ—Ä. –ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ķ, —á–Ķ –Ĺ–ł–Ķ —ā—ä—Ä—Ā–ł–ľ –Ņ—Ä–ł–ľ–Ķ—Ä–ł –∑–į –Ņ–ĺ—Ä—Ź–ī—ä–ļ, —ā–į–ļ–į —á–Ķ –Ĺ–į–Ļ-–ī–ĺ–Ī—Ä–ł—ā–Ķ –ļ–ĺ–Ĺ—ā—Ä–į–Ņ—Ä–ł–ľ–Ķ—Ä–ł –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –ł–ľ–į—ā –ľ–Ĺ–ĺ–≥–ĺ –Ī–Ķ–∑–Ņ–ĺ—Ä—Ź–ī—ä–ļ - —ā–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į—ā —Ā–Ľ—É—á–į–Ļ–Ĺ–ł. –Ę–ĺ–≤–į –∑–į—ā—Ä—É–ī–Ĺ—Ź–≤–į –ł–Ľ–ł –Ņ—Ä–į–≤–ł –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į "–Ņ—Ä–į–≤–ł–Ľ–ĺ", –ļ–ĺ–Ķ—ā–ĺ –ī–į –ī–į–≤–į –ī–ĺ–Ī—Ä–ł –ļ–ĺ–Ĺ—ā—Ä–į–Ņ—Ä–ł–ľ–Ķ—Ä–ł. –í—Ā—Ź–ļ–ĺ –Ĺ–Ķ—Č–ĺ, –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ł—Ä–į–Ĺ–ĺ –Ņ–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ, –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ —Č–Ķ –ł–ľ–į —ā–≤—ä—Ä–ī–Ķ –ľ–Ĺ–ĺ–≥–ĺ —Ä–Ķ–ī –≤ –Ĺ–Ķ–≥–ĺ.
–ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į –≥–ĺ—Ä–Ĺ–ł—ā–Ķ –Ĺ–ł –≥—Ä–į–Ĺ–ł—Ü–ł –ľ–ĺ–∂–Ķ –ī–į —Ā–į —ā–≤—ä—Ä–ī–Ķ –≤–ł—Ā–ĺ–ļ–ł, –Ĺ–ĺ –ļ–į–ļ —Č–Ķ –≥–ĺ –ī–ĺ–ļ–į–∂–Ķ–ľ? –ú–ĺ–∂–Ķ –Ī–ł –ļ–į—ā–ĺ —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –≤—Ā–ł—á–ļ–ł –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä? –Ě–ĺ –Ķ–ī–ł–Ĺ –Ņ—Ä–ĺ—Ā—ā –Ņ—Ä–ł–ľ–Ķ—Ä —Č–Ķ –Ņ–ĺ–ļ–į–∂–Ķ, —á–Ķ —ā–ĺ–≤–į –Ĺ–ł–ļ–ĺ–≥–į –Ĺ—Ź–ľ–į –ī–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–ł. –Ē–į –ļ–į–∂–Ķ–ľ, —á–Ķ –ł—Ā–ļ–į–ľ–Ķ –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ R(5,5) –Ķ –Ĺ–į–Ļ-–ľ–Ĺ–ĺ–≥–ĺ 54 - —Ā –ī—Ä—É–≥–ł –ī—É–ľ–ł, –ī–į –Ņ–ĺ–ļ–į–∂–Ķ–ľ, —á–Ķ 54 —ā–ĺ—á–ļ–ł –≤–ł–Ĺ–į–≥–ł —Č–Ķ –≥–į—Ä–į–Ĺ—ā–ł—Ä–į—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į 5 —ā–ĺ—á–ļ–ł, –≤—Ā–ł—á–ļ–ł —Ā–≤—ä—Ä–∑–į–Ĺ–ł –Ņ–ĺ–ľ–Ķ–∂–ī—É —Ā–ł —Ā –Ľ–ł–Ĺ–ł–ł —Ā –Ķ–ī–ł–Ĺ —Ü–≤—Ź—ā. –©–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –≤—Ā–ł—á–ļ–ł –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł –Ĺ–į—á–ł–Ĺ–ł –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į –Ľ–ł–Ĺ–ł–ł—ā–Ķ –ľ–Ķ–∂–ī—É 54 —ā–ĺ—á–ļ–ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ.
–ö–ĺ–Ľ–ļ–ĺ –Ĺ–į—á–ł–Ĺ–į –ł–ľ–į? –ü—ä—Ä–≤–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –∑–Ĺ–į–Ķ–ľ –Ī—Ä–ĺ—Ź –Ĺ–į –Ľ–ł–Ĺ–ł–ł—ā–Ķ, –ļ–ĺ–Ļ—ā–ĺ –Ņ–ĺ –ī–ĺ–Ī—Ä–Ķ –Ņ–ĺ–∑–Ĺ–į—ā–į—ā–į —Ą–ĺ—Ä–ľ—É–Ľ–į –Ķ
(54 √ó 53) / 2 = 1431.
–í—Ā—Ź–ļ–į –Ľ–ł–Ĺ–ł—Ź –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–į –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ, —ā–į–ļ–į —á–Ķ –Ī—Ä–ĺ—Ź—ā –Ĺ–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł—ā–Ķ –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–ł—Ź –Ķ —ā–į–ļ—ä–≤
2 √ó 2 √ó 2 √ó ... √ó 2,
–ļ—ä–ī–Ķ—ā–ĺ –Ī—Ä–ĺ—Ź—ā –Ĺ–į 2-–ļ–ł—ā–Ķ, —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł –∑–į–Ķ–ī–Ĺ–ĺ, –Ķ 1431 - –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –∑–į–Ņ–ł—Ā¬†—ā–ĺ–≤–į –Ķ 2 1431 –ł–Ľ–ł –Ĺ–į–ī 10 400. –Ę–ĺ–≤–į —á–ł—Ā–Ľ–ĺ –Ķ –ľ–Ĺ–ĺ–≥–ĺ, –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–ĺ –ĺ—ā –Ī—Ä–ĺ—Ź –Ĺ–į —á–į—Ā—ā–ł—Ü–ł—ā–Ķ –≤ –Ņ–ĺ–∑–Ĺ–į—ā–į—ā–į –í—Ā–Ķ–Ľ–Ķ–Ĺ–į (–ĺ–ļ–ĺ–Ľ–ĺ 10 80 ). –Ę–į–ļ–į —á–Ķ –Ĺ—Ź–ľ–į –Ĺ–ł–ļ–į–ļ—ä–≤ —ą–į–Ĺ—Ā –ī–ĺ—Ä–ł –ł –Ĺ–į–Ļ-–Ī—ä—Ä–∑–ł—Ź—ā –≤—ä–∑–ľ–ĺ–∂–Ķ–Ĺ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä –ī–į –∑–į–≤—ä—Ä—ą–ł —ā–į–ļ–ĺ–≤–į —ā—ä—Ä—Ā–Ķ–Ĺ–Ķ. –Ę–ĺ–≤–į –Ķ –∑–į–≥–į–ī–ļ–į, —á–ł–Ļ—ā–ĺ –ĺ—ā–≥–ĺ–≤–ĺ—Ä –ľ–ĺ–∂–Ķ –Ī–ł –Ĺ–ł–ļ–ĺ–≥–į –Ĺ—Ź–ľ–į –ī–į —É–∑–Ĺ–į–Ķ–ľ.
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –Ņ–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł—Ź
–ü–ĺ–Ľ –ē—Ä–ī—Ć–ĺ—ą (Paul ErdŇĎs), –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–∑ 1935 –≥. —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į, —á–Ķ –≥–ĺ—Ä–Ĺ–į—ā–į –≥—Ä–į–Ĺ–ł—Ü–į –∑–į –≤—Ā—Ź–ļ–ĺ —á–ł—Ā–Ľ–ĺ –Ĺ–į –†–į–ľ–∑–ł –Ķ 4 –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į —Ä–į–∑–ľ–Ķ—Ä–į –Ĺ–į –ļ–Ľ–ł–ļ–į—ā–į, –≤–Ķ–ī–Ĺ—ä–∂ –ļ–į–∑–≤–į, —á–Ķ –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–ĺ—á–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ –Ĺ–į –†–į–ľ–∑–ł –∑–į –ļ–Ľ–ł–ļ–į –ĺ—ā —ą–Ķ—Ā—ā –ī—É—ą–ł –Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į —ā—Ä—É–ī–Ĺ–ĺ, —á–Ķ –į–ļ–ĺ –ł–∑–≤—ä–Ĺ–∑–Ķ–ľ–Ĺ–ł—ā–Ķ –Ņ–ĺ–ł—Ā–ļ–į—ā –ī–į —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –≥–ĺ –ł–∑—á–ł—Ā–Ľ–ł–ľ –ł–Ľ–ł –ī–į –Ī—ä–ī–Ķ–ľ —É–Ĺ–ł—Č–ĺ–∂–Ķ–Ĺ–ł, –Ĺ—Ź–ľ–į –ī–į –ł–ľ–į–ľ–Ķ –ī—Ä—É–≥ –ł–∑–Ī–ĺ—Ä, –ĺ—Ā–≤–Ķ–Ĺ –ī–į —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –≥–ł –į—ā–į–ļ—É–≤–į–ľ–Ķ –Ņ—ä—Ä–≤–ł. –ě—ā—ā–ĺ–≥–į–≤–į –Ĺ–į—Ā–į–ľ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł —Ā–į —Ā–Ķ –ĺ–Ņ–ł—ā–≤–į–Ľ–ł –ī–į –Ņ–ĺ–ī–ĺ–Ī—Ä—Ź—ā –∑–Ĺ–į—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –≥—Ä–į–Ĺ–ł—Ü–į—ā–į –Ĺ–į –ē—Ä–ī—Ć–ĺ—ą, –Ĺ–ĺ –Ī–Ķ–∑ –ĺ—Ā–ĺ–Ī–Ķ–Ĺ —É—Ā–Ņ–Ķ—Ö.
–°–Ķ–≥–į –Ē–∂—É–Ľ–ł—ä–Ĺ –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ (Julian Sahasrabudhe) –ĺ—ā –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –≤ –ö–Ķ–Ļ–ľ–Ī—Ä–ł–ī–∂ –ł –Ĺ–Ķ–≥–ĺ–≤–ł—ā–Ķ –ļ–ĺ–Ľ–Ķ–≥–ł –Ņ–ĺ–ļ–į–∑–≤–į—ā, —á–Ķ –≥–ĺ—Ä–Ĺ–į—ā–į –≥—Ä–į–Ĺ–ł—Ü–į –∑–į —á–ł—Ā–Ľ–į—ā–į –Ĺ–į –†–į–ľ–∑–ł –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ĺ–į–ľ–į–Ľ–Ķ–Ĺ–į –ĺ—ā 4 –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į —Ä–į–∑–ľ–Ķ—Ä–į –Ĺ–į –ļ–Ľ–ł–ļ–į—ā–į –ī–ĺ 3.993 –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į —Ä–į–∑–ľ–Ķ—Ä–į –Ĺ–į –ļ–Ľ–ł–ļ–į—ā–į.
"–ě—ā—Ā—ā—Ä–į–Ĺ–ł –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ĺ—Ź–ļ–į–ļ –≥–Ľ—É–Ņ–į–≤–ĺ - –ļ–į—ā–ĺ —á–Ķ –Ľ–ł, –ī–ĺ–Ī—Ä–Ķ, –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ —Ā–Ķ –ĺ–Ņ–ł—ā–≤–į—ā –ī–į –Ņ–ĺ–ī–ĺ–Ī—Ä—Ź—ā –Ĺ—Ź–ļ–į–ļ–≤–ĺ —á–ł—Ā–Ľ–ĺ –ł –Ĺ–į –ļ–ĺ–≥–ĺ –ľ—É –Ņ—É–ļ–į?", –ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ. "–Ě–ĺ —ā–ĺ–≤–į, –ļ–ĺ–Ķ—ā–ĺ –Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ĺ –≤ —ā–Ķ–∑–ł –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–ł –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł, –ļ–į—ā–ĺ —Ä–į–∑–Ľ–ł–ļ–į—ā–į –ľ–Ķ–∂–ī—É –≥—Ä–į–Ĺ–ł—Ü–į—ā–į –Ĺ–į –ē—Ä–ī—Ć–ĺ—ą –ł –Ņ—Ä–Ķ–ī–ł—ą–Ĺ–ł—ā–Ķ –≥—Ä–į–Ĺ–ł—Ü–ł –ł –Ĺ–į—ą–į—ā–į —Ä–į–Ī–ĺ—ā–į, –Ķ, —á–Ķ –Ĺ–į–ł—Ā—ā–ł–Ĺ–į –ł–ľ–į –Ĺ—Ź–ļ–į–ļ–≤–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ–Ĺ–ł–Ķ, –ļ–ĺ–Ķ—ā–ĺ –ĺ—ā—Ä–į–∑—Ź–≤–į –∑–į–ī—ä–Ľ–Ī–ĺ—á–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ĺ–į—ą–Ķ—ā–ĺ —Ä–į–∑–Ī–ł—Ä–į–Ĺ–Ķ –∑–į [–ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—ā–Ķ] —Ā—ā—Ä—É–ļ—ā—É—Ä–ł."
–°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ –ł –ļ–ĺ–Ľ–Ķ–≥–ł—ā–Ķ –ľ—É –∑–į–Ņ–ĺ—á–≤–į—ā –ī–į —Ä–į–Ī–ĺ—ā—Ź—ā –Ņ–ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –Ņ—Ä–Ķ–∑ 2018 –≥. –≤ –Ě–į—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ł—Ź –ł–Ĺ—Ā—ā–ł—ā—É—ā –∑–į —á–ł—Ā—ā–į –ł –Ņ—Ä–ł–Ľ–ĺ–∂–Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –≤ –†–ł–ĺ –ī–Ķ –Ė–į–Ĺ–Ķ–Ļ—Ä–ĺ, –Ď—Ä–į–∑–ł–Ľ–ł—Ź.
"–Ę–ĺ–≤–į –Ķ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ł –Ĺ–ł–Ķ –ł–ľ–į—Ö–ľ–Ķ –Ĺ—Ź–ļ–ĺ–ł –ł–ī–Ķ–ł - –ł –ł–∑–≥–Ľ–Ķ–∂–ī–į—ą–Ķ, —á–Ķ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –≤—ä—Ä–≤–ł –ī–ĺ—Ā—ā–į –ī–ĺ–Ī—Ä–Ķ, –ļ–ĺ–Ķ—ā–ĺ –Ī–Ķ—ą–Ķ –≤—ä–Ľ–Ĺ—É–≤–į—Č–ĺ", —Ä–į–∑–ļ–į–∑–≤–į –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ.
–ü—Ä–Ķ–∑ –Ņ—ä—Ä–≤–ł—ā–Ķ –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ľ–Ķ—Ā–Ķ—Ü–į –Ķ–ļ–ł–Ņ—ä—ā –Ķ –Ĺ–į—á–Ķ—Ä—ā–į–Ľ –≥—Ä—É–Ī –Ņ–Ľ–į–Ĺ –∑–į —ā–ĺ–≤–į –ļ–į–ļ –Ī–ł –ľ–ĺ–≥–Ľ–ĺ –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ, –ĺ–Ī—Ź—Ā–Ĺ—Ź–≤–į –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ, –Ĺ–ĺ –Ī—ä—Ä–∑–ĺ —Ā–Ķ –Ķ —Ā–Ī–Ľ—ä—Ā–ļ–į–Ľ —Ā –Ņ—Ä–Ķ–Ņ—Ź—ā—Ā—ā–≤–ł–Ķ, –ļ–ĺ–Ķ—ā–ĺ –Ķ –≤–ļ–Ľ—é—á–≤–į–Ľ–ĺ –ł–∑—á–ł—Ā–Ľ—Ź–≤–į–Ĺ–Ķ –Ĺ–į —ā–ĺ–≤–į –ļ–į–ļ —ā–ĺ—á–ļ–ł—ā–Ķ —Ā–Ķ —Ā—ā—Ä—É–Ņ–≤–į—ā –Ķ–ī–Ĺ–į –ī–ĺ –ī—Ä—É–≥–į –≤—ä—Ä—Ö—É —Ā—Ą–Ķ—Ä–ł –ĺ—ā –≤–ł—Ā–ĺ–ļ–ł –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź.
–°–Ľ–Ķ–ī –ļ–į—ā–ĺ –≥–ĺ–ī–ł–Ĺ–ł –Ĺ–į—Ä–Ķ–ī —Ā–Ķ –ĺ–Ņ–ł—ā–≤–į—ā –ī–į —Ä–Ķ—ą–į—ā —ā–ĺ–∑–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ł –Ĺ–Ķ —É—Ā–Ņ—Ź–≤–į—ā, –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ –ł –Ķ–ļ–ł–Ņ—ä—ā –ľ—É —Ä–į–∑–Ī–ł—Ä–į—ā, —á–Ķ –ľ–ĺ–≥–į—ā –ī–į –Ņ—Ä–Ķ—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į—ā –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ —Ā–ł, –∑–į –ī–į –ł–∑–Ī–Ķ–≥–Ĺ–į—ā –ł–∑—Ü—Ź–Ľ–ĺ –≤—ä–Ņ—Ä–ĺ—Ā–į —Ā—ä—Ā —Ā—Ą–Ķ—Ä–ł—ā–Ķ, —Ā–Ľ–Ķ–ī –ļ–ĺ–Ķ—ā–ĺ –Ĺ–Ķ—Č–į—ā–į –Ī—ä—Ä–∑–ĺ –Ĺ–į–Ņ—Ä–Ķ–ī–≤–į—ā. "–í–ľ–Ķ—Ā—ā–ĺ –ī–į –Ņ—Ä–Ķ–ļ–ĺ—Ā–ł–ľ –Ņ–Ľ–į–Ĺ–ł–Ĺ–į—ā–į, —Ä–į–∑–Ī—Ä–į—Ö–ľ–Ķ, —á–Ķ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –ľ–ĺ–∂–Ķ–ľ –Ĺ—Ź–ļ–į–ļ –ī–į —Ź –∑–į–ĺ–Ī–ł–ļ–ĺ–Ľ–ł–ľ", —Ä–į–∑–ļ–į–∑–≤–į –°–į—Ö–į—Ā—Ä–į–Ī—É–ī–Ķ.
–ě–ļ–ĺ–Ĺ—á–į—ā–Ķ–Ľ–Ĺ–ĺ—ā–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ķ –ī—ä–Ľ–≥–ĺ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 50 —Ā—ā—Ä–į–Ĺ–ł—Ü–ł –ł –Ņ—Ä–Ķ–ī—Ā—ā–ĺ–ł –ī–į –Ī—ä–ī–Ķ –ĺ—Ą–ł—Ü–ł–į–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ä–Ķ–Ĺ–ĺ, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł –ĺ—ā –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ĺ—ā–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į –ē—Ä–ī—Ć–ĺ—ą, –ļ–ĺ–Ķ—ā–ĺ –≤–ļ–Ľ—é—á–≤–į —É–≤–Ķ–Ľ–ł—á–į–≤–į–Ĺ–Ķ –Ĺ–į –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–ł —Ö–ĺ—Ä–į –≤ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ĺ –≥–ĺ–Ľ–Ķ–ľ–ł –Ņ–į—Ä—ā–ł—ā–į –ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ĺ–Ķ –Ĺ–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł—ā–Ķ –∑–į –≤—Ä—ä–∑–ļ–ł—ā–Ķ –ł–ľ —Ā —ā–Ķ—Ö–Ĺ–ł—ā–Ķ —Ā—ä—Ā–Ķ–ī–ł, –į —Ā—ä—Č–ĺ –ł –ł–ī–Ķ–Ĺ—ā–ł—Ą–ł—Ü–ł—Ä–į–Ĺ–Ķ –Ĺ–į —Ā—ä—Ā–Ķ–ī–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł –Ĺ–į –ļ–Ľ–ł–ļ–ł, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–ł "–ļ–Ĺ–ł–≥–ł" (‚Äúbooks‚ÄĚ), –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ–ĺ-–Ľ–Ķ—Ā–Ĺ–ł –∑–į –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ, –Ĺ–ĺ –≥–į—Ä–į–Ĺ—ā–ł—Ä–į—ā, —á–Ķ –ļ–Ľ–ł–ļ–ł —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā.
"–ü–ĺ–Ĺ–Ķ –Ņ—Ä–Ķ–∑ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ 50 –≥–ĺ–ī–ł–Ĺ–ł –≤—Ā–Ķ–ļ–ł –ł–∑—ā—ä–ļ–Ĺ–į—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ¬†–≤ –ľ–ĺ—Ź—ā–į –ĺ–Ī–Ľ–į—Ā—ā —Ā–Ķ –Ķ –ĺ–Ņ–ł—ā–≤–į–Ľ –ī–ĺ—Ā—ā–į —É—Ā–ł–Ľ–Ķ–Ĺ–ĺ –ī–į –Ņ–ĺ–ī–ĺ–Ī—Ä–ł —ā–Ķ–∑–ł –≥—Ä–į–Ĺ–ł—Ü–ł –ł –Ĺ–Ķ –Ķ —É—Ā–Ņ—Ź–Ľ",¬†–ĺ—ā–Ī–Ķ–Ľ—Ź–∑–≤–į –Ē–Ķ–Ļ–≤–ł–ī –ö–ĺ–Ĺ–Ľ–ĺ–Ĺ (David Conlon) –ĺ—ā –ö–į–Ľ–ł—Ą–ĺ—Ä–Ĺ–ł–Ļ—Ā–ļ–ł—Ź —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ–Ĺ –ł–Ĺ—Ā—ā–ł—ā—É—ā. "–§–į–ļ—ā—ä—ā, —á–Ķ —Ā–Ķ–≥–į —ā–Ķ —Ā–į –Ņ–ĺ–ī–ĺ–Ī—Ä–ł–Ľ–ł —ā–ĺ–∑–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā, –Ķ –ľ–Ĺ–ĺ–≥–ĺ –≤–į–∂–Ķ–Ĺ."
–°–Ķ–≥–į, —Ā–Ľ–Ķ–ī –ļ–į—ā–ĺ –Ī–į—Ä–ł–Ķ—Ä–į—ā–į –ĺ—ā 4 –Ķ –Ņ—Ä–Ķ–ĺ–ī–ĺ–Ľ—Ź–Ĺ–į, –ī—Ä—É–≥–ł –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ľ–ĺ–≥–į—ā –ī–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –ł –ĺ–Ņ—ā–ł–ľ–ł–∑–ł—Ä–į—ā –ľ–Ķ—ā–ĺ–ī–ł—ā–Ķ –Ĺ–į –°–į—Ö–į—Ā—Ä–į–Ī—É–ī—Ö–Ķ –ł –Ĺ–Ķ–≥–ĺ–≤–ł—Ź –Ķ–ļ–ł–Ņ, –∑–į –ī–į –Ņ–ĺ–Ľ—É—á–į—ā —á–ł—Ā–Ľ–ĺ, –ľ–į–Ľ–ļ–ĺ –Ņ–ĺ-–Ĺ–ł—Ā–ļ–ĺ –ĺ—ā 3,993.
"–Ę–ĺ–≤–į –Ķ –ī—Ź–≤–ĺ–Ľ—Ā–ļ–ł —ā—Ä—É–ī–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ", –ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į –ü–ł—ā—ä—Ä –ö–į–ľ–Ķ—Ä—ä–Ĺ (Peter Cameron) –ĺ—ā –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į "–°–Ķ–Ļ–Ĺ—ā –ź–Ĺ–ī—Ä—é—Ā", –í–Ķ–Ľ–ł–ļ–ĺ–Ī—Ä–ł—ā–į–Ĺ–ł—Ź. "–ú–į–Ľ–ļ–ĺ –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ–Ĺ–ł–Ķ –ļ–į—ā–ĺ —ā–ĺ–≤–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –ĺ–≥—Ä–ĺ–ľ–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–ł–≤ –≤ —ā–Ķ—Ö–Ĺ–ł–ļ–ł—ā–Ķ –∑–į —Ä–Ķ—ą–į–≤–į–Ĺ–Ķ—ā–ĺ –ľ—É."
–°–Ņ—Ä–į–≤–ļ–į:¬†–ö—É—Ä—Ā–ĺ–≤–į —Ä–į–Ī–ĺ—ā–į –Ņ–ĺ –ß–ł—Ā–Ľ–į –Ĺ–į –†–Ķ–ľ–∑–ł,¬†–°–£ ‚Äě–°–≤. –ö–Ľ–ł–ľ–Ķ–Ĺ—ā –ě—Ö—Ä–ł–ī—Ā–ļ–ł‚Ä̬†
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
Friends and strangers, Plus Magazine, University of Cambridge, Imre Leader
–ź–≤—ā–ĺ—Ä—ä—ā –ė–ľ—Ä–Ķ –õ–ł–ī–Ķ—Ä –Ķ —Ā—ä—ā—Ä—É–ī–Ĺ–ł–ļ –Ĺ–į –ļ–ĺ–Ľ–Ķ–∂–į –Ę—Ä–ł–Ĺ–ł—ā–ł –≤ –ö–Ķ–Ļ–ľ–Ī—Ä–ł–ī–∂ –ł –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ –≤ –ļ–į—ā–Ķ–ī—Ä–į—ā–į –Ņ–ĺ —á–ł—Ā—ā–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į –Ĺ–į —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –≤ –ö–Ķ–Ļ–ľ–Ī—Ä–ł–ī–∂.
Breakthrough in fiendishly hard puzzle has mathematicians partying, New Scientist
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –∑–į–ī "R –Ĺ—É–Ľ–į", —Ā—ā–į–ī–Ĺ–ł—Ź—ā –ł–ľ—É–Ĺ–ł—ā–Ķ—ā –ł –Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –≤–į–ļ—Ā–ł–Ĺ–ł—ā–Ķ

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–©–ĺ –Ķ —ā–ĺ –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā–Ĺ–į –≥—Ä–Ķ—ą–ļ–į?
–Ė–ł–≤–ĺ—ā—ä—ā
–ö–į–ļ —Ā–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ķ–Ņ–ł–ī–Ķ–ľ–ł—Ź—ā–į?


















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
4I4ATA
–Ě–ĺ–≤, —Ā–ļ—Ä–ł—ā –ī–ĺ—Ā–Ķ–≥–į –≤—Ö–ĺ–ī –≤ –Ņ–ł—Ä–į–ľ–ł–ī–į—ā–į –Ĺ–į –ú–ł–ļ–Ķ—Ä–ł–Ĺ –Ķ –ĺ—ā–ļ—Ä–ł—ā –Ņ–ĺ –į–Ĺ–ĺ–ľ–į–Ľ–ł–ł –Ņ—Ä–ł —Ā–ļ–į–Ĺ–ł—Ä–į–Ĺ–Ķ
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews