

–Ď—Ä–ł—ā–į–Ĺ—Ā–ļ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ-–Ľ—é–Ī–ł—ā–Ķ–Ľ –ě–Ī—Ä–ł –ī–Ķ –ď—Ä–Ķ–Ļ –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –∑–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ 60 –≥–ĺ–ī–ł–Ĺ–ł –Ņ–ĺ–ī–ĺ–Ī—Ä–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–į –≤ —Ä–Ķ—ą–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –∑–į —Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į.
–Ę–ĺ–≤–į —á–ł—Ā–Ľ–ĺ –Ķ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ł—Ź—ā –Ī—Ä–ĺ–Ļ —Ü–≤–Ķ—ā–ĺ–≤–Ķ, —Ā –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–∂–Ķ —ā–į–ļ–į –ī–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā–ł —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į, —á–Ķ –ī–į –Ĺ—Ź–ľ–į –ī–≤–Ķ —ā–ĺ—á–ļ–ł —Ā –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā–į–Ĺ—ā–ł–ľ–Ķ—ā—ä—Ä). –Ę–į–∑–ł –∑–į–ī–į—á–į –Ĺ–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –Ī—ä—Ä–ļ–į —Ā –Ņ–ĺ–ī–ĺ–Ī–Ĺ–į—ā–į, –Ĺ–ĺ –≤–Ķ—á–Ķ —Ä–Ķ—ą–Ķ–Ĺ–į –∑–į–ī–į—á–į –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į –ļ–į—Ä—ā–ł.
–ü–ĺ-—Ä–į–Ĺ–ĺ –Ī–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á–Ķ —Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į –Ľ–Ķ–∂–ł –ľ–Ķ–∂–ī—É 4 –ł 7, –Ĺ–ĺ –ī–Ķ –ď—Ä–Ķ–Ļ –Ņ–ĺ–ļ–į–∑–į, —á–Ķ¬†—Ā 4 —Ü–≤—Ź—ā–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā–ł —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į. –ü—Ä–Ķ–Ņ—Ä–ł–Ĺ—ā –Ĺ–į –Ĺ–Ķ–≥–ĺ–≤–į—ā–į —Ä–į–Ī–ĺ—ā–į –Ķ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–į –≤ arXiv.org, –į —Ā–Ķ–≥–į —Ā–Ķ –Ņ—Ä–ĺ–≤–Ķ—Ä—Ź–≤–į –ĺ—ā –ī—Ä—É–≥–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł.
–í –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ź —Ā–≤—Ź—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ņ—Ä–į–ļ—ā–ł–ļ–į—ā–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł —É—á–Ķ–Ĺ–ł –ł–Ľ–ł –ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł–ł –ī–į —Ā—ä—Ā—ā–į–≤—Ź—ā —Ā–Ņ–ł—Ā—ä—Ü–ł —Ā –Ī–Ķ—Ä–Ķ—ą–Ķ–Ĺ–ł –∑–į–ī–į—á–ł, –į–ļ—ā—É–į–Ľ–Ĺ–ł –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į. –Ę–į–ļ—ä–≤ –Ķ —Ā–Ņ–ł—Ā—ä–ļ—ä—ā –Ĺ–į –ė–Ĺ—Ā—ā–ł—ā—É—ā–į –ö–Ľ–Ķ–Ļ —Ā—ä—Ā –∑–į–ī–į—á–ł—ā–Ķ –Ĺ–į —Ö–ł–Ľ—Ź–ī–ĺ–Ľ–Ķ—ā–ł–Ķ—ā–ĺ, –∑–į —Ä–Ķ—ą–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ļ–ĺ–ł—ā–ĺ –ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł—Ź—ā–į –ī–į–≤–į 1 –ľ–ł–Ľ–ł–ĺ–Ĺ –ī–ĺ–Ľ–į—Ä–į.¬†
–°–Ķ–≥–į –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ - –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ĺ–į –•–į–ī–≤–ł–≥–Ķ—Ä-–Ě–Ķ–Ľ—Ā—ä–Ĺ (Hadwiger-Nelson) - –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –ĺ—ā –Ņ–ĺ–≤–Ķ—á–Ķ 60 –≥–ĺ–ī–ł–Ĺ–ł –Ī–Ķ –Ņ–ĺ—Ā—ā–ł–≥–Ĺ–į—ā –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ –ĺ—ā –Ķ–ī–ł–Ĺ –Ľ—é–Ī–ł—ā–Ķ–Ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ, –Ī–ł–ĺ–Ľ–ĺ–≥–į –ě–Ī—Ä–ł –ī–Ķ –ď—Ä–Ķ–Ļ (Aubrey de Grey), –Ņ–ĺ—Ā–≤–Ķ—ā–ł–Ľ –∂–ł–≤–ĺ—ā–į —Ā–ł –ī–į —Ä–į–∑–Ī–Ķ—Ä–Ķ –ļ–į–ļ –ľ–ĺ–∂–Ķ–ľ –ī–į –∂–ł–≤–Ķ–Ķ–ľ –Ņ–ĺ-–ī—ä–Ľ–≥–ĺ –ł –ľ–ĺ–∂–Ķ –Ī–ł, –≤–Ķ—á–Ĺ–ĺ.¬†
–ď—Ä–į—Ą–ĺ–≤–Ķ –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ
–ü—Ä–Ķ–∑ 1950 –≥.¬† –ē–ī—É–į—Ä–ī –Ě–Ķ–Ľ—Ā—ä–Ĺ, —ā–ĺ–≥–į–≤–į —Ā—ā—É–ī–Ķ–Ĺ—ā –≤ –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –≤ –ß–ł–ļ–į–≥–ĺ, –∑–į–ī–į–ī–Ķ –Ķ–ī–ł–Ĺ –Ņ—Ä–ł–≤–ł–ī–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā –≤—ä–Ņ—Ä–ĺ—Ā, –ļ–ĺ–Ļ—ā–ĺ –ł–∑–ľ—ä—á–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –≤ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī–Ķ—Ā–Ķ—ā–ł–Ľ–Ķ—ā–ł—Ź. –ü—Ä–Ķ–ī—Ā—ā–į–≤–Ķ—ā–Ķ —Ā–ł, –ļ–į–∑–≤–į —ā–ĺ–Ļ, –≥—Ä–į—Ą - –ļ–ĺ–Ľ–Ķ–ļ—Ü–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –Ľ–ł–Ĺ–ł–ł. –£–≤–Ķ—Ä–Ķ—ā–Ķ —Ā–Ķ, —á–Ķ –≤—Ā–ł—á–ļ–ł –Ľ–ł–Ĺ–ł–ł —Ā–į —Ā –Ķ–ī–Ĺ–į –ł —Ā—ä—Č–į –ī—ä–Ľ–∂–ł–Ĺ–į –ł —á–Ķ –≤—Ā–ł—á–ļ–ĺ –Ķ —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ĺ –≤ —Ä–į–≤–Ĺ–ł–Ĺ–į. –°–Ķ–≥–į –ĺ—Ü–≤–Ķ—ā–Ķ—ā–Ķ –≤—Ā–ł—á–ļ–ł —ā–ĺ—á–ļ–ł , —ā–į–ļ–į —á–Ķ –ī–į –Ĺ—Ź–ľ–į –ī–≤–Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ł —ā–ĺ—á–ļ–ł —Ā –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā. –Ě–Ķ–Ľ—Ā—ä–Ĺ –Ņ–ł—ā–į: "–ö–ĺ–Ļ –Ķ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ł—Ź –Ī—Ä–ĺ–Ļ —Ü–≤–Ķ—ā–ĺ–≤–Ķ, —Ā –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –ĺ—Ü–≤–Ķ—ā–ł—ā–Ķ —ā–į–ļ—ä–≤ –≥—Ä–į—Ą, –ī–ĺ—Ä–ł –ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ —á—Ä–Ķ–∑ —Ā–≤—ä—Ä–∑–≤–į–Ĺ–Ķ –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –≤—ä—Ä—Ö–ĺ–≤–Ķ?
–Ę–į–∑–ł –∑–į–ī–į—á–į –Ķ –Ņ–ĺ–∑–Ĺ–į—ā–į —Ā–Ķ–≥–į –ļ–į—ā–ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā "–•–į–ī–∂–ł–≥–Ķ—Ä-–Ě–Ķ–Ľ—Ā—ä–Ĺ" –ł–Ľ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į —Ā –Ĺ–į–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į. –Ę—Ź¬†–Ņ—Ä–Ķ–ī–ł–∑–≤–ł–ļ–≤ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–į –Ĺ–į –ľ–Ĺ–ĺ–≥–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł. –Ę–Ķ –Ī—ä—Ä–∑–ĺ –Ĺ–į–ľ–į–Ľ–ł—Ö–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł—ā–Ķ, –ļ–į—ā–ĺ —É—Ā—ā–į–Ĺ–ĺ–≤–ł—Ö–į, —á–Ķ –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –≥—Ä–į—Ą –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ —Ā –Ĺ–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā —á–Ķ—ā–ł—Ä–ł –ł –Ĺ–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā —Ā–Ķ–ī–Ķ–ľ —Ü–≤—Ź—ā–į.¬†
 Wikimedia Commons
Wikimedia Commons
–õ–Ķ—Ā–Ĺ–ĺ –Ķ –ī–į —Ā–Ķ –ī–ĺ–ļ–į–∂–Ķ, —á–Ķ –ī–≤–į —Ü–≤—Ź—ā–į –Ĺ–Ķ —Ā–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į. –Ě–Ķ–ļ–į –Ĺ–į—Ä–ł—Ā—É–≤–į–ľ–Ķ –Ĺ–į—ą–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į –≤ –ī–≤–į —Ü–≤—Ź—ā–į. –ü–ĺ—Ā–Ľ–Ķ –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ —Ä–į–≤–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–į—ā–į –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –ü—ä—Ä–≤–ł—Ź—ā –≤—Ä—ä—Ö –Ķ —Ā–ł–Ĺ, –≤—ā–ĺ—Ä–ł—Ź—ā –Ķ —á–Ķ—Ä–≤–Ķ–Ĺ. –ė –ļ–į–ļ—ä–≤ —Ü–≤—Ź—ā —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ —ā—Ä–Ķ—ā–ł—Ź—ā –≤—Ä—ä—Ö? –Ę—ä–Ļ –ļ–į—ā–ĺ –Ķ –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ķ–ī–ł–Ĺ–ł—Ü–į –ĺ—ā –Ņ—ä—Ä–≤–ł—ā–Ķ –ī–≤–į, —ā–ĺ–Ļ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ĺ–ł—ā–ĺ –≤ —Ā–ł–Ĺ—Ć–ĺ, –Ĺ–ł—ā–ĺ –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ. –ú–į–Ľ–ļ–ĺ –Ņ–ĺ-—ā—Ä—É–ī–Ĺ–ĺ –Ķ –ī–į —Ā–Ķ –Ņ–ĺ–ļ–į–∂–Ķ, —á–Ķ —ā—Ä–ł —Ü–≤—Ź—ā–į —Ā–į –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł. –ó–į –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł —ā–ĺ–≤–į, –Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł —ā.–Ĺ–į—Ä. –≤—Ä–Ķ—ā–Ķ–Ĺ–ĺ –Ĺ–į –ú–ĺ–∑–Ķ—Ä - –ī–į –≤–∑–Ķ–ľ–Ķ–ľ –Ķ–ī–ł–Ĺ —Ä–ĺ–ľ–Ī, —Ā—ä—Ā—ā–ĺ—Ź—Č —Ā–Ķ –ĺ—ā –ī–≤–į —Ā—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ł –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į. –Ē–į –Ĺ–į–Ņ—Ä–į–≤–ł–ľ –ļ–ĺ–Ņ–ł–Ķ –Ĺ–į –Ĺ–Ķ–≥–ĺ –ł –ī–į –≥–ĺ –∑–į–≤—ä—Ä—ā–ł–ľ –ĺ–ļ–ĺ–Ľ–ĺ –Ķ–ī–ł–Ĺ –ĺ—ā –≤—ä—Ä—Ö–ĺ–≤–Ķ—ā–Ķ –Ĺ–į —Ä–ĺ–ľ–Ī–į (–ī–į –≥–ĺ –Ĺ–į—Ä–Ķ—á–Ķ–ľ "–≥–ĺ—Ä–Ķ–Ĺ"), –ļ–į—ā–ĺ –Ĺ–į–Ņ—Ä–į–≤–ł–ľ —ā–į–ļ–į, —á–Ķ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É –ī–≤–į—ā–į –ī–ĺ–Ľ–Ĺ–ł –≤—ä—Ä—Ö–į –Ķ –Ķ–ī–ł–Ĺ–ł—Ü–į. –õ–Ķ—Ā–Ĺ–ĺ –Ķ –ī–į —Ā–Ķ –≤–ł–ī–ł –ļ–į—ā–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –ĺ—Ü–≤–Ķ—ā–ł–ľ –≤—Ä–Ķ—ā–Ķ–Ĺ–ĺ—ā–ĺ –Ĺ–į –ú–ĺ–∑–Ķ—Ä, —á–Ķ —ā—Ä–ł—ā–Ķ —Ü–≤—Ź—ā–į –∑–į —ā–į–∑–ł —Ą–ł–≥—É—Ä–į –Ĺ–Ķ —Ā—ā–ł–≥–į—ā.
–Ē–ĺ–ļ–į–∑–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ—ā–ĺ –≤ —Ā–Ķ–ī–Ķ–ľ —Ü–≤—Ź—ā–į —Ā—ä—Č–ĺ –Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ - —ā–ĺ –Ņ–ĺ–≤—ā–į—Ä—Ź –Ņ—á–Ķ–Ľ–Ĺ–į—ā–į –Ņ–ł—ā–į. –Ē–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –Ķ —Ā–į–ľ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł –ľ—Ä–Ķ–∂–į –Ĺ–į –Ņ—á–Ķ–Ľ–Ĺ–ł –ļ—É—ā–ł–Ļ–ļ–ł –ĺ—ā –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ł —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–į 0,4.
–Ę–į–ļ–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ķ —Ā–≤–Ķ–ī–Ķ–Ĺ –ī–ĺ –Ķ–ī–Ĺ–ĺ –ĺ—ā —á–ł—Ā–ļ–į—ā–į 4, 5, 6 –ł–Ľ–ł 7, –Ĺ–ĺ –Ĺ–Ķ –Ī–Ķ –Ņ–ĺ—Ā—ā–ł–≥–Ĺ–į—ā –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ –ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –ĺ—Ā—ā–į–Ĺ–į –Ĺ–Ķ—Ä–Ķ—ą–Ķ–Ĺ. –Ě—Ź–ļ–ĺ–ł –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ī–ĺ–ļ–į–∑–į—Ö–į –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ —á–į—Ā—ā–ł—á–Ĺ–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł –Ņ—Ä–Ķ–∑ —Ā–Ľ–Ķ–ī–≤–į—Č–ł—ā–Ķ –ī–Ķ—Ā–Ķ—ā–ł–Ľ–Ķ—ā–ł—Ź, –Ĺ–ĺ –Ĺ–ł–ļ–ĺ–Ļ –Ĺ–Ķ —É—Ā–Ņ—Ź –ī–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł —ā–Ķ–∑–ł –≥—Ä–į–Ĺ–ł—Ü–ł. –Ē–ĺ–ļ–į—ā–ĺ –Ĺ–Ķ —Ā–Ķ –Ĺ–į–ľ–Ķ—Ā–ł –ě–Ī—Ä–ł –ī–Ķ –ď—Ä–Ķ–Ļ.
–Ď–ł–ĺ–Ľ–ĺ–≥—ä—ā, –ļ–ĺ–Ļ—ā–ĺ –ĺ—Ā—ā–į–≤–ł –ł–ľ–Ķ—ā–ĺ —Ā–ł –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į

–Ē–Ķ –ď—Ä–Ķ–Ļ¬†–Ĺ–Ķ –Ķ –Ņ—Ä–ĺ—Ą–Ķ—Ā–ł–ĺ–Ĺ–į–Ľ–Ķ–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ, –Ĺ–Ķ–≥–ĺ–≤–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–ł –Ľ–Ķ–∂–į—ā –Ņ–ĺ–≤–Ķ—á–Ķ –≤ –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į –≥–Ķ—Ä–ĺ–Ĺ—ā–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł—ā–Ķ –Ĺ–į —Ā—ā–į—Ä–Ķ–Ķ–Ĺ–Ķ—ā–ĺ. –Ę–ĺ–Ļ —Ä—ä–ļ–ĺ–≤–ĺ–ī–ł —Ą–ĺ–Ĺ–ī–į—Ü–ł—Ź—ā–į SENS, –ļ–ĺ—Ź—ā–ĺ —Ä–į–∑—Ä–į–Ī–ĺ—ā–≤–į —Ā—ā—Ä–į—ā–Ķ–≥–ł–ł –∑–į –Ņ–ĺ—Ā—ā–ł–≥–į–Ĺ–Ķ –Ĺ–į "–Ņ—Ä–Ķ–ľ–į—Ö–≤–į–Ĺ–Ķ –Ĺ–į –Ĺ–Ķ–≥–į—ā–ł–≤–Ĺ–ł—ā–Ķ –Ķ—Ą–Ķ–ļ—ā–ł –ĺ—ā —Ā—ā–į—Ä–Ķ–Ķ–Ĺ–Ķ—ā–ĺ" —á—Ä–Ķ–∑ –ł–Ĺ–∂–Ķ–Ĺ–Ķ—Ä–Ĺ–ł –ľ–Ķ—ā–ĺ–ī–ł. –Ď–ł–ĺ–Ľ–ĺ–≥—ä—ā, –ļ–ĺ–Ļ—ā–ĺ –≤–Ķ–ī–Ĺ—ä–∂ –Ĺ–į–Ņ—Ä–į–≤–ł —Ā–ľ–Ķ–Ľ–ĺ—ā–ĺ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ, —á–Ķ —Ö–ĺ—Ä–į—ā–į, –ļ–ĺ–ł—ā–ĺ –∂–ł–≤–Ķ—Ź—ā –ī–Ĺ–Ķ—Ā, —Č–Ķ –∂–ł–≤–Ķ—Ź—ā¬†–ī–ĺ 1000 –≥–ĺ–ī–ł–Ĺ–ł, –ī–Ķ –ď—Ä–Ķ–Ļ –ĺ–Ī–ł—á–į –ī–į —Ā–ł –Ņ–ĺ—á–ł–≤–į –ĺ—ā —ā–Ķ–ļ—É—Č–į—ā–į —Ā–ł —Ä–į–Ī–ĺ—ā–į, –ļ–į—ā–ĺ —Ä–Ķ—ą–į–≤–į –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł –ĺ—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į.
–ė —É—Ā–Ņ—Ź–≤–į. –í —Ā—ā–į—ā–ł—Ź—ā–į —Ā–ł "–•—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į –Ķ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ĺ 5" —ā–ĺ–Ļ –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į, —á–Ķ —Ä–į–≤–Ĺ–ł–Ĺ–Ķ–Ĺ –≥—Ä–į—Ą —Ā —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ķ–ī–ł–Ĺ–ł—Ü–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ —Ā–į–ľ–ĺ —Ā —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ē–Ķ –ď—Ä–Ķ–Ļ –Ķ –≤–ī—ä—Ö–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –ĺ—ā –ł–≥—Ä–į—ā–į –Ĺ–į –ī—ä—Ā–ļ–į "–ě—ā–Ķ–Ľ–ĺ" (–Ĺ–į—Ä–ł—á–į–Ĺ–į –ł –†–Ķ–≤–Ķ—Ä—Ā–ł), –ļ–ĺ—Ź—ā–ĺ –Ĺ–į–Ņ–ĺ–ľ–Ĺ—Ź¬†–Ĺ–į –ł–≥—Ä–į—ā–į "–ď–ĺ".¬†–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł—Ź—ā –≤–į—Ä–ł–į–Ĺ—ā —Ā–Ķ –ł–≥—Ä–į–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ī—ä—Ā–ļ–į —Ā –ļ–≤–į–ī—Ä–į—ā–ł 8 x 8. –¶–Ķ–Ľ—ā–į –Ĺ–į –ł–≥—Ä–į—ā–į –Ķ –ī–į –ł–ľ–į—ą –Ņ–ĺ–≤–Ķ—á–Ķ —Ą–ł–≥—É—Ä–ł –Ĺ–į –ī—ä—Ā–ļ–į—ā–į –ĺ—ā —Ā–≤–ĺ—Ź –Ņ—Ä–ĺ—ā–ł–≤–Ĺ–ł–ļ. –ė–≥—Ä–į—ā–į –Ņ—Ä–ł–ļ–Ľ—é—á–≤–į, –ļ–ĺ–≥–į—ā–ĺ –≤—Ā–ł—á–ļ–ł –ļ–≤–į–ī—Ä–į—ā—á–Ķ—ā–į —Ā–į –∑–į–Ķ—ā–ł —Ā —Ą–ł–≥—É—Ä–ł –ł–Ľ–ł –Ĺ–ł—ā–ĺ –Ķ–ī–ł–Ĺ –ĺ—ā –ī–≤–į–ľ–į—ā–į –Ņ—Ä–ĺ—ā–ł–≤–Ĺ–ł—Ü–ł –Ĺ–į –ľ–ĺ–∂–Ķ –ī–į –Ĺ–į–Ņ—Ä–į–≤–ł —Ö–ĺ–ī.
 –ė–≥—Ä–į—ā–į "–ě—ā–Ķ–Ľ–ĺ". Paul_012 / Wikipedia
–ė–≥—Ä–į—ā–į "–ě—ā–Ķ–Ľ–ĺ". Paul_012 / Wikipedia
–ü—Ä–Ķ–ī–ł –ī–Ķ—Ā–Ķ—ā–ł–Ĺ–į –≥–ĺ–ī–ł–Ĺ–ł –ī–Ķ –ď—Ä–Ķ–Ļ –ļ–į—ā–ĺ –∑–į–Ņ–į–Ľ–Ķ–Ĺ –ł–≥—Ä–į—á –Ĺ–į "–ě—ā–Ķ–Ľ–ĺ" —Ā–Ķ —Ā—Ä–Ķ—Č–į —Ā –Ĺ—Ź–ļ–ĺ–ł —ā–į–Ľ–į–Ĺ—ā–Ľ–ł–≤–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł, –ļ–ĺ–ł—ā–ĺ –≥–ĺ –∑–į–Ņ–ĺ–∑–Ĺ–į–≤–į—ā —Ā —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≥—Ä–į—Ą–ł—ā–Ķ –ł —ā–ĺ–Ļ —Ā–Ķ –≤—Ä—ä—Č–į –ļ—ä–ľ –Ĺ–Ķ—Ź –ĺ—ā –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –≤—Ä–Ķ–ľ–Ķ. –ė –ĺ–ļ–ĺ–Ľ–嬆–ö–ĺ–Ľ–Ķ–ī–į –ľ–ł–Ĺ–į–Ľ–į—ā–į –≥–ĺ–ī–ł–Ĺ–į —ā–ĺ–Ļ –Ņ—Ä–į–≤–ł –Ņ—Ä–ĺ–Ī–ł–≤–į —Ā–ł.
"–ü–ĺ–Ĺ—Ź–ļ–ĺ–≥–į, –ļ–ĺ–≥–į—ā–ĺ –ł–ľ–į–ľ –Ĺ—É–∂–ī–į –ĺ—ā –Ņ–ĺ—á–ł–≤–ļ–į –ĺ—ā –ł—Ā—ā–ł–Ĺ—Ā–ļ–į—ā–į —Ā–ł —Ä–į–Ī–ĺ—ā–į, –ľ–ł—Ā–Ľ–Ķ—Ö –∑–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į",¬†–ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į —ā–ĺ–Ļ –≤ Quanta magazine.¬†
"–ė–ľ–į—Ö –ł–∑–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ķ–Ĺ –ļ—ä—Ā–ľ–Ķ—ā - —Ā–Ņ–ĺ–ī–Ķ–Ľ—Ź –ī–Ķ –ď—Ä–Ķ–Ļ. "–Ě–Ķ –≤—Ā–Ķ–ļ–ł –ī–Ķ–Ĺ –Ĺ—Ź–ļ–ĺ–Ļ –ł–∑–Ľ–ł–∑–į —Ā —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į 60-–≥–ĺ–ī–ł—ą–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ".
–ß–Ķ—ā–ł—Ä–ł—Ü–≤–Ķ—ā–Ĺ–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į
–í —Ā—ā–į—ā–ł—Ź—ā–į —Ā–ł, –ī–Ķ –ď—Ä–Ķ–Ļ –Ķ –Ņ–ĺ–ļ–į–∑–į–Ľ –ļ–į–ļ –ī–į —Ā–Ķ –ł–∑–≥—Ä–į–ī–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–į –ĺ—ā 1567 –≤—ä—Ä—Ö–ĺ–≤–Ķ, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł —Ā —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į, —ā–į–ļ–į —á–Ķ –Ĺ—Ź–ľ–į –ī–≤–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ, –ļ–ĺ–ł—ā–ĺ –ī–į –Ĺ–Ķ —Ā–į –≤ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā. –ö–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź—ā–į —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā —á–Ķ—ā–ł—Ä–ł —Ā—ā—ä–Ņ–ļ–ł.
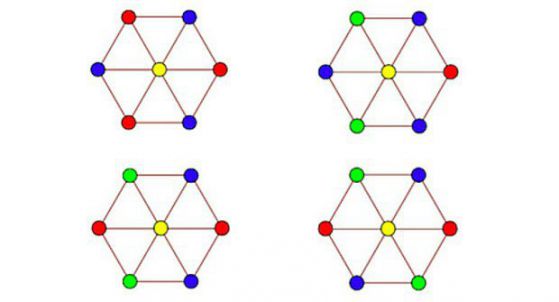
–ě—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ—ā–ĺ –ĺ—ā–≥–ĺ—Ä–Ķ —Ā—ä–ī—ä—Ä–∂–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –į –ĺ—ā–ī–ĺ–Ľ—É - –Ĺ–Ķ. Aubrey D.N.J. –ī–Ķ –ď—Ä–Ķ–Ļ / arXiv.org, 2018
–Ē–į¬†–Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –Ņ—Ä–į–≤–ł–Ľ–Ķ–Ĺ —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į, –ī–į –Ņ–ĺ—Ā—ā–į–≤–ł–ľ —ā–ĺ—á–ļ–į¬†–≤ —Ü–Ķ–Ĺ—ā—ä—Ä–į –ľ—É –ł –ī–į —Ź —Ā–≤—ä—Ä–∂–Ķ–ľ —Ā –≤—ä—Ä—Ö–ĺ–≤–Ķ—ā–Ķ, —ā—Ź —Č–Ķ —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ķ–ī–ł–Ĺ–ł—Ü–į –ĺ—ā –≤—Ā–Ķ–ļ–ł –≤—Ä—ä—Ö. –Ē–į —Ā–Ķ –ĺ–Ņ–ł—ā–į–ľ–Ķ –ī–į –≥–ĺ –Ī–ĺ—Ź–ī–ł—Ā–į–ľ–Ķ –≤ —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į –Ņ–ĺ –≤—Ā–ł—á–ļ–ł –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł –Ĺ–į—á–ł–Ĺ–ł. –ě–ļ–į–∑–≤–į —Ā–Ķ, —á–Ķ –ł–ľ–į —Ā–į–ľ–ĺ —á–Ķ—ā–ł—Ä–ł –ļ–ĺ—Ä–Ķ–Ĺ–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–ł—Ź –Ĺ–į —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ–į, –Ņ—Ä–ł —ā–ĺ–≤–į –≤ –ī–≤–Ķ –ĺ—ā —ā—Ź—Ö —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į—ā —Ä–į–≤–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ĺ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–ł, —Ä–į–≤–Ĺ–ł –Ĺ–į –ļ–ĺ—Ä–Ķ–Ĺ –ļ–≤–į–ī—Ä–į—ā–Ķ–Ĺ –ĺ—ā —ā—Ä–ł, –≤—Ā–ł—á–ļ–ł –≤—ä—Ä—Ö–ĺ–≤–Ķ –Ĺ–į –ļ–ĺ–ł—ā–ĺ —Ā–į –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł —Ā –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā. –Ē–Ķ –ď—Ä–Ķ–Ļ –≥–ł –Ĺ–į—Ä–ł—á–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–Ĺ–ł —ā—Ä–ĺ–Ļ–ļ–ł.
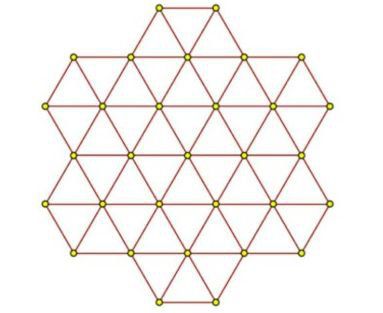
–ě—Ā–Ĺ–ĺ–≤–į—ā–į –∑–į –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ –Ĺ–į —Ą–ł–≥—É—Ä–į, —Ā—ä–ī—ä—Ä–∂–į—Č–į –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ĺ –Ķ–ī–Ĺ–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–Ĺ–į —ā—Ä–ĺ–Ļ–ļ–į. Aubrey D.N.J. de Grey / arXiv.org, 2018
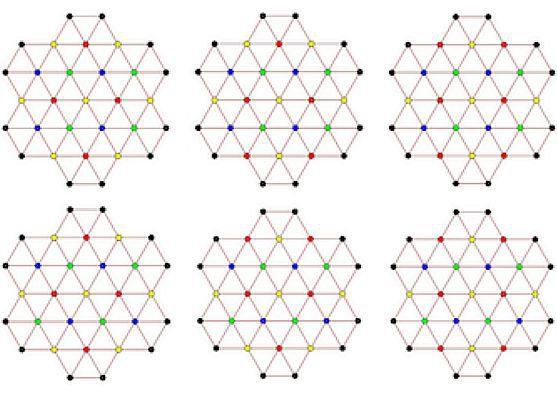
–ě–ļ–į–∑–≤–į —Ā–Ķ, —á–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł —ā–į–ļ—ä–≤ –≥—Ä–į—Ą, –≤ –ļ–ĺ–Ļ—ā–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–į —ā—Ä–ĺ–Ļ–ļ–į. –Ę–ĺ–Ļ —Č–Ķ —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā 52 —ā–į–ļ–ł–≤–į —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł, –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ĺ —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł –≤ —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į. –Ě–į–ļ—Ä–į—ā–ļ–ĺ, –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ –∑–į–Ņ–ĺ—á–≤–į —Ā —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ –ĺ—ā —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –ĺ—ā –≥–ĺ—Ä–Ĺ–ł—Ź –į–Ī–∑–į—Ü, –ļ–ĺ–Ļ—ā–ĺ —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–Ķ —É–ī–≤–ĺ—Ź–≤–į –ł —Ā–Ķ –∑–į–≤—ä—Ä—ā–į –ĺ–ļ–ĺ–Ľ–ĺ —Ü–Ķ–Ĺ—ā—ä—Ä–į, –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–Ņ—Ä—Ź–ľ–ĺ –≤—ä—Ä—Ö–į –Ľ–Ķ–∂–ł –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ī–≤–Ķ –ĺ—ā —Ü–Ķ–Ĺ—ā—ä—Ä–į.
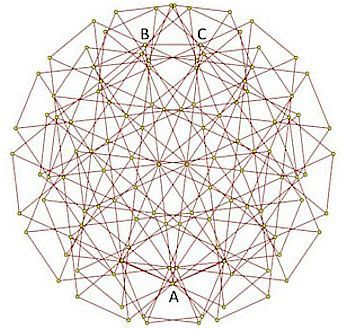
–°–ļ–Ķ–Ľ–Ķ—ā –ĺ—ā 52 —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ–į, –≤ –ļ–ĺ–ł—ā–ĺ –≥–į—Ä–į–Ĺ—ā–ł—Ä–į–Ĺ–ĺ –≤—ä–∑–Ĺ–ł–ļ–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ —ā—Ä–ĺ–Ļ–ļ–į. Aubrey D.N.J. –ī–Ķ –ď—Ä–Ķ–Ļ / arXiv.org, 2018
–í—ā–ĺ—Ä–į—ā–į —á–į—Ā—ā –Ĺ–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ –Ķ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł –≥—Ä–į—Ą, –≤ –ļ–ĺ–Ļ—ā–ĺ –≤—ä–∑–Ĺ–ł–ļ–≤–į —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–ł –Ĺ–ł—ā–ĺ –Ķ–ī–ł–Ĺ –≤–į—Ä–ł–į–Ĺ—ā –Ĺ–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –ł–ľ–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–į —ā—Ä–ĺ–Ļ–ļ–į. –Ę–ĺ–Ļ —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –≥–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ —Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł –≤—Ä–Ķ—ā–Ķ–Ĺ–į –Ĺ–į –ú–ĺ–∑–Ķ—Ä, –ļ–ĺ–ł—ā–ĺ —Ā–į —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł –ĺ–ļ–ĺ–Ľ–ĺ –Ķ–ī–ł–Ĺ —ą–Ķ—Ā—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł –ł–ľ–į—ā 1345 –≤—ä—Ä—Ö–į. –í —Ā–Ľ–Ķ–ī–≤–į—Č–ł—Ź –Ķ—ā–į–Ņ –Ĺ–į –ī–Ķ –ď—Ä–Ķ–Ļ –ļ–ĺ–Ņ–ł—Ä–į —ā–ĺ–∑–ł –≥—Ä–į—Ą 52 –Ņ—ä—ā–ł, —ā–į–ļ–į —á–Ķ –Ĺ–Ķ–≥–ĺ–≤–į —á–į—Ā—ā –ī–į —Ā–Ķ –ĺ–ļ–į–∂–Ķ –≥—Ä–į—Ą—ä—ā –ĺ—ā¬† –Ņ—Ä–Ķ–ī—Ö–ĺ–ī–Ĺ–ł—Ź –į–Ī–∑–į—Ü, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ĺ–Ķ–Ņ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ –≤—ä–∑–Ĺ–ł–ļ–≤–į –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–Ĺ–į —ā—Ä–ĺ–Ļ–ļ–į. –ü–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź—ā —Ā–ļ–Ķ–Ľ–Ķ—ā —Ā 20425 –≤—ä—Ä—Ö–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ –≤ —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į, —ā—ä–Ļ –ļ–į—ā–ĺ –≤ –Ņ—Ä–ĺ—ā–ł–≤–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ –≤—ä–∑–Ĺ–ł–ļ–≤–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ķ.
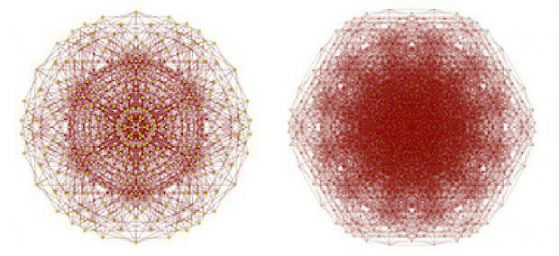
–°–ļ–Ķ–Ľ–Ķ—ā,¬†–≤ —Ü–Ķ–Ĺ—ā—ä—Ä–į –Ĺ–į –ļ–ĺ–Ļ—ā–ĺ –≥–į—Ä–į–Ĺ—ā–ł—Ä–į–Ĺ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –≤—ä–∑–Ĺ–ł–ļ–Ķ –ľ–ĺ–Ĺ–ĺ—Ö—Ä–ĺ–ľ–į—ā–ł—á–Ĺ–į —ā—Ä–ĺ–Ļ–ļ–į (–≤–ī—Ź—Ā–Ĺ–ĺ). –í–į–Ľ—Ź–≤–ĺ - –Ņ—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–į—ā–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į –∑–į –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ. Aubrey D.N.J. de Grey / arXiv.org, 2018
–Ē–Ķ –ď—Ä–Ķ–Ļ¬†—Ā–Ķ –ĺ–Ņ–ł—ā–į –ī–į –ĺ–Ņ—Ä–ĺ—Ā—ā–ł —ā–ĺ–∑–ł —Ā–ļ–Ķ–Ľ–Ķ—ā, –Ĺ–ĺ –Ĺ–į–Ļ-–ī–ĺ–Ī—ä—Ä —Ä–Ķ–∑—É–Ľ—ā–į—ā –ī–į–ī–Ķ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź —Ā 1567 –≤—ä—Ä—Ö–į, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į —á—Ä–Ķ–∑ –Ņ—Ä–Ķ–ľ–į—Ö–≤–į–Ĺ–Ķ –Ĺ–į —á–į—Ā—ā –ĺ—ā —ā–ĺ—á–ļ–ł—ā–Ķ. –̖嬆—Ā–Ľ–Ķ–ī –Ņ–ĺ—Ā–Ľ–Ķ–ī–≤–į—Č–į—ā–į –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–į —Ā–Ķ –ĺ–ļ–į–∑–į, —á–Ķ –≤—Ā–Ķ –Ņ–į–ļ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ī–ĺ—Ź–ī–ł—Ā–į –≤ —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į, –Ĺ–ĺ —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į¬† –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į –Ņ—Ä–ł–ľ–Ķ—Ä–į —Ā 1581 –≤—ä—Ä—Ö–į, –ļ–ĺ–Ļ—ā–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā–ł —Ā –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –ĺ—ā 5 —Ü–≤—Ź—ā–į.¬†
–ź–ļ–ĺ –ł–∑–≤–ĺ–ī—ä—ā –ĺ—ā —Ā—ā–į—ā–ł—Ź—ā–į –ī–Ķ –ď—Ä–Ķ–Ļ —Ā–Ķ –Ņ–ĺ—ā–≤—ä—Ä–ī–ł, —á–Ķ —Č–Ķ –Ī—ä–ī–Ķ –Ķ–ī–ł–Ĺ –ĺ—ā —Ä–Ķ–ī–ļ–ł—ā–Ķ —Ā–Ľ—É—á–į–ł, –ļ–ĺ–≥–į—ā–ĺ —ā—Ä—É–ī–Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –∑–į–ī–į—á–į, –ļ–ĺ—Ź—ā–ĺ –Ķ –∑–į–Ĺ–ł–ľ–į–≤–į–Ľ–į –≥–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ —Ā–Ņ–Ķ—Ü–ł–į–Ľ–ł—Ā—ā–ł, —Ā–Ķ —Ä–Ķ—ą–į–≤–į –ĺ—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ-–Ľ—é–Ī–ł—ā–Ķ–Ľ. –ü—Ä–Ķ–ī–ł—ą–Ĺ–ł—Ź—ā —Ā–Ľ—É—á–į–Ļ, —Ā–≤—ä—Ä–∑–į–Ĺ —Ā –Ņ–ĺ–ļ—Ä–ł–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į —Ā –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–ľ–ł—Ü–ł, –Ī–Ķ –Ņ—Ä–Ķ–∑ 1976 –≥. –ł 1977 –≥. –ĺ—ā –ú–į—Ä–ī–∂—ä—Ä–ł –†–į–Ļ—Ā, –ī–ĺ–ľ–į–ļ–ł–Ĺ—Ź, –Ī–Ķ–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ.
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–§–ł–∑–ł–ļ–į
–£—á–Ķ–Ĺ–ł –ĺ–Ī—Ź—Ā–Ĺ—Ź–≤–į—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ļ–≤–į–∑–ł–ļ—Ä–ł—Ā—ā–į–Ľ–Ĺ–į—ā–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–ú–į—ā–Ķ–ľ–į—ā–ł—Ü–ł —Ö–≤—ä—Ä–Ľ–ł—Ö–į –ľ–ĺ—Ā—ā –Ņ—Ä–Ķ–∑ –Ņ—Ä–ĺ–Ņ–į—Ā—ā—ā–į –ľ–Ķ–∂–ī—É –ļ—Ä–į–Ļ–Ĺ–ĺ –ł –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–ē–ļ–∑–ĺ—ā–ł—á–Ĺ–ł –Ĺ–į—á–ł–Ĺ–ł –∑–į —Ä–į–∑—Ä—Ź–∑–≤–į–Ĺ–Ķ –Ĺ–į –Ņ–ł—Ü–į




















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.