

–ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł¬†—É—Ā–Ņ—Ź–≤–į—ā –ī–į —Ä–Ķ—ą–į—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ĺ—ā 80-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł –ĺ—ā –ľ–ł–Ĺ–į–Ľ–ł—Ź –≤–Ķ–ļ¬†–ł –Ņ–ĺ–ļ–į–∑–≤–į—ā –≥–ĺ–Ľ—Ź–ľ–į —á–į—Ā—ā –ĺ—ā —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –≤ –Ĺ–į—É—á–Ĺ–į —Ā—ā–į—ā–ł—Ź.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –∑–į –Ņ–ĺ–ī–ĺ–Ī—Ä—Ź–≤–į–Ĺ–Ķ –Ĺ–į –Ī—ä–ī–Ķ—Č–ł—ā–Ķ —ā–Ķ–Ľ–Ķ—Ą–ĺ–Ĺ–ł –ł –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł.
–Ē–≤–į–ľ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł —É—á–Ķ–Ĺ–ł, –ī–ĺ—Ü. –Ē–∂–Ķ–Ļ–ļ—ä–Ī –•–ĺ–Ľ–ľ (Jacob Holm) –ĺ—ā –ö–ĺ–Ņ–Ķ–Ĺ—Ö–į–≥–Ķ–Ĺ—Ā–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā UCPH –ł –ī–ĺ—Ü–Ķ–Ĺ—ā –ē–≤–į –†–ĺ—ā–Ķ–Ĺ–Ī–Ķ—Ä–≥ (Eva Rotenberg) –ĺ—ā –Ē–į—ā—Ā–ļ–ł—Ź –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā DTU,¬†—Ä–Ķ—ą–į–≤–į—ā¬†–ī—ä–Ľ–≥–ĺ–≥–ĺ–ī–ł—ą–Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–į, —Ā–Ľ–Ķ–ī –ļ–į—ā–ĺ –ī–Ķ—Ā–Ķ—ā–ł–Ľ–Ķ—ā–ł—Ź –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ –Ĺ–Ķ —É—Ā–Ņ—Ź—Ö–į –ī–į –Ņ–ĺ—Ā—ā–ł–≥–Ĺ–į—ā –∑–Ĺ–į—á–ł—ā–Ķ–Ľ–Ķ–Ĺ –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ –Ņ–ĺ –≤—ä–Ņ—Ä–ĺ—Ā–į –ĺ—ā 90-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł.
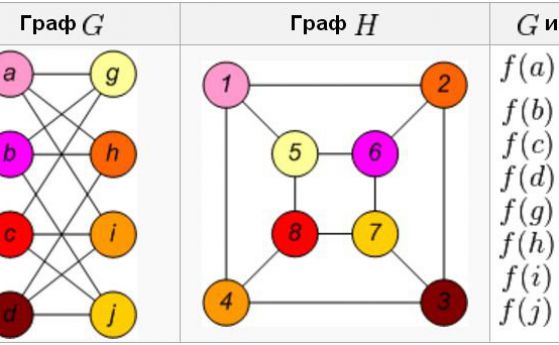
–í—ä–Ņ—Ä–ĺ—Ā–Ĺ–ł—Ź—ā –į–Ī—Ā—ā—Ä–į–ļ—ā–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –Ķ —á–į—Ā—ā –ĺ—ā —ā.–Ĺ–į—Ä.¬†—ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –≥—Ä–į—Ą–ł—ā–Ķ –ł —Ā–Ķ –ĺ—ā–Ĺ–į—Ā—Ź –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–ĺ –ī–ĺ –Ņ—Ä–Ķ–ī–ł–∑–≤–ł–ļ–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ –ī–į —Ā–Ķ –Ĺ–į–ľ–Ķ—Ä–ł –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –∑–į —Ä–Ķ—ą–į–≤–į–Ĺ–Ķ –Ĺ–į –Ņ–Ľ–į—Ä–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ī–ł–Ĺ–į–ľ–ł—á–Ķ–Ĺ –≥—Ä–į—Ą. –Ę–ĺ–≤–į –ľ–ĺ–∂–Ķ –ī–į –∑–≤—É—á–ł –ľ–į–Ľ–ļ–ĺ –ĺ—ā–≤–Ľ–Ķ—á–Ķ–Ĺ–ĺ, –Ĺ–ĺ –ł–ľ–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–∑–į–Ī–į–≤–Ķ–Ĺ –ł –ī–ĺ—Ā—ā—ä–Ņ–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –∑–į –ĺ—Ā–ľ–ł—Ā–Ľ—Ź–Ĺ–Ķ –Ĺ–į —Ā—ä—Č–ł—ā–Ķ –ł–ī–Ķ–ł.
–ě—ā 1913 –≥. - –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –Ņ—Ä–ĺ—Ā–Ľ–Ķ–ī–Ķ–Ĺ–ł –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–ī–į–Ľ–Ķ—á - –Ī–Ķ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–į –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–į, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į¬†–Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł.
–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł
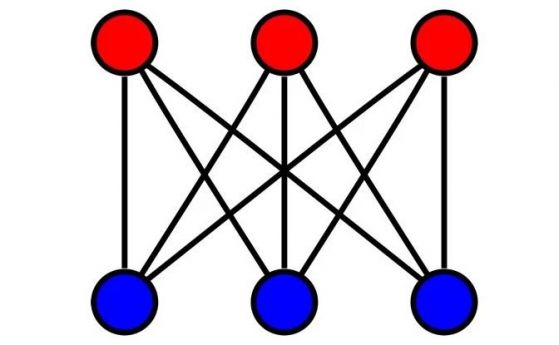
–ü—Ä–Ķ–∑ 1913 –≥. –Ņ—Ä–Ķ–ī—ą–Ķ—Ā—ā–≤–Ķ–Ĺ–ł–ļ—ä—ā –Ĺ–į —Ā–Ķ–≥–į —Ä–Ķ—ą–į–≤–į–Ĺ–į—ā–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–į –Ķ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ –≤ —Ā–Ņ–ł—Ā–į–Ĺ–ł–Ķ ‚ÄěStrand‚Äú –ļ–į—ā–ĺ ‚Äě–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł‚Äú. –Ę–ĺ–Ļ¬†–∑–į—ā—Ä—É–ī–Ĺ–ł¬†—á–ł—ā–į—ā–Ķ–Ľ–ł—ā–Ķ –Ĺ–į —Ā–Ņ–ł—Ā–į–Ĺ–ł–Ķ—ā–ĺ. –ü—Ä–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –≤—Ā—Ź–ļ–į –ĺ—ā —ā—Ä–ł –ļ—ä—Č–ł —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –≤–ĺ–ī–į, –≥–į–∑ –ł –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā—ā–≤–ĺ, –ī–ĺ–ļ–į—ā–ĺ "–Ņ—Ä–ĺ–≤–ĺ–ī–ł—ā–Ķ" –ľ–Ķ–∂–ī—É –ļ—ä—Č–ł—ā–Ķ –ł –≤–ĺ–ī–į—ā–į, –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ł –≥–į–∑—ā–į¬†—ā—Ä—Ź–Ī–≤–į –ī–į –Ĺ–Ķ —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā –Ķ–ī–Ĺ–į –ī—Ä—É–≥–į - –ļ–ĺ–Ķ—ā–ĺ –Ĺ–Ķ –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ.
–Ě–ĺ –ļ–ĺ–≥–į—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ —É—Ā—ā–į–Ĺ–ĺ–≤–ł, —á–Ķ –Ĺ–Ķ—Č–ĺ –Ķ –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ, —ā–ĺ–Ļ –ľ–ł—Ā–Ľ–ł: –ú–ĺ–≥–į –Ľ–ł –ī–į –ī–ĺ–ļ–į–∂–į, —á–Ķ –Ĺ–į–ł—Ā—ā–ł–Ĺ–į –Ķ –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ? –ė –ľ–ĺ–≥–į –Ľ–ł –ī–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —É—Ā–Ľ–ĺ–≤–ł—Ź—ā–į, –∑–į –ī–į –Ĺ–į–Ņ—Ä–į–≤—Ź —ā–ĺ–≤–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ?¬†
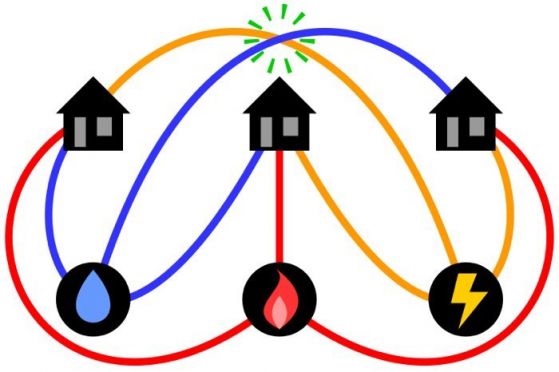 –†–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł —Ā –Ķ–ī–Ĺ–ĺ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –ö—Ä–Ķ–ī–ł—ā:¬†CMG Lee / Wikimedia Commons / CC BY-SA 4.0¬†
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł —Ā –Ķ–ī–Ĺ–ĺ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –ö—Ä–Ķ–ī–ł—ā:¬†CMG Lee / Wikimedia Commons / CC BY-SA 4.0¬†
–Ě–į –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ, –ī–≤—É–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ –Ľ–ł—Ā—ā —Ö–į—Ä—ā–ł—Ź, –ļ–į—ā–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –Ņ–Ľ–į–Ĺ–į—Ä–Ķ–Ĺ –≥—Ä–į—Ą,¬†–Ĺ–Ķ –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į —Ā–Ķ —Ä–Ķ—ą–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł.¬†
–Ě–ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł –Ĺ–Ķ –Ķ –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–į, –ļ–ĺ–Ļ—ā–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ —Ä–Ķ—ą–Ķ–Ĺ–į, –į –Ņ–ĺ-—Ā–ļ–ĺ—Ä–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į —ā–ĺ–≤–į,¬†—á–Ķ –Ĺ—Ź–ļ–ĺ–ł –≤–ł–ī–ĺ–≤–Ķ –≥—Ä–į—Ą–ĺ–≤–ł –ľ—Ä–Ķ–∂–ł –ľ–ĺ–∂–Ķ –ī–į –Ĺ–Ķ —Ā–į –Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ł - —ā.–Ķ. –ľ–ĺ–≥–į—ā –ī–į –ł–ľ–į—ā —Ä–Ķ–Ī—Ä–į (–Ľ–ł–Ĺ–ł–ł), —Ā–≤—ä—Ä–∑–≤–į—Č–ł —Ä–į–∑–Ľ–ł—á–Ĺ–ł—ā–Ķ —Ā–ł –≤—ä—Ä—Ö–ĺ–≤–Ķ (–ļ—ä—Č–ł –ł –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł) –Ī–Ķ–∑ –Ľ–ł–Ĺ–ł–ł—ā–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā.¬†
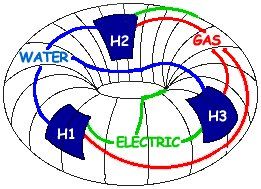 –í—ä—Ä—Ö—É —ā–ĺ—Ä (–Ņ–ĺ–Ĺ–ł—á–ļ–į) –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł —Ā–Ķ —Ä–Ķ—ą–į–≤–į –Ī–Ķ–∑ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –ö—Ä–Ķ–ī–ł—ā:¬†http://mathforum.org/dr.math/faq/faq.3utilities.html
–í—ä—Ä—Ö—É —ā–ĺ—Ä (–Ņ–ĺ–Ĺ–ł—á–ļ–į) –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł —Ā–Ķ —Ä–Ķ—ą–į–≤–į –Ī–Ķ–∑ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –ö—Ä–Ķ–ī–ł—ā:¬†http://mathforum.org/dr.math/faq/faq.3utilities.html
–ó–į —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≥—Ä–į—Ą–ł—ā–Ķ
–ď—Ä–į—Ą—ä—ā¬†–Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā–į –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–į –∑–į –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į–Ĺ–Ķ –Ĺ–į –Ĺ–Ķ—Č–į, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ĺ–Ņ–ł—Ā–į–Ĺ–ł –ļ–į—ā–ĺ –ĺ–Ī–Ķ–ļ—ā–ł –ł –≤—Ä—ä–∑–ļ–ł—ā–Ķ –ľ–Ķ–∂–ī—É —ā—Ź—Ö. –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≥—Ä–į—Ą–ł—ā–Ķ –Ķ –Ķ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ –ĺ–Ī–Ľ–į—Ā—ā –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –ł –≤–į–∂–Ķ–Ĺ –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā –≤ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł—ā–Ķ –Ĺ–į—É–ļ–ł.
–í —ā–ĺ–∑–ł –ļ–ĺ–Ĺ—ā–Ķ–ļ—Ā—ā –≥—Ä–į—Ą—ä—ā –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ł–Ľ—é—Ā—ā—Ä–ł—Ä–į–Ĺ —á—Ä–Ķ–∑ —Ā—Ö–Ķ–ľ–į, —Ā—ä—Ā—ā–ĺ—Ź—Č–į —Ā–Ķ –ĺ—ā –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į —ā–ĺ—á–ļ–ł (–≤—ä–∑–Ľ–ł, –≤—ä—Ä—Ö–ĺ–≤–Ķ), —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į –Ľ–ł–Ĺ–ł–ł (—Ä–Ķ–Ī—Ä–į). –í—Ā—Ź–ļ–ĺ —Ä–Ķ–Ī—Ä–ĺ —Ā–Ķ –ł–Ľ—é—Ā—ā—Ä–ł—Ä–į –ļ–į—ā–ĺ –Ľ–ł–Ĺ–ł—Ź (–ł–Ľ–ł –ļ—Ä–ł–≤–į) —Ā –≤—ä–∑–Ľ–ł¬†–≤ –ī–≤–Ķ—ā–Ķ —Ā–ł –ļ—Ä–į–Ļ–Ĺ–ł —ā–ĺ—á–ļ–ł.
–°–Ņ–ĺ—Ä–Ķ–ī —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –Ĺ–į –ě–Ļ–Ľ–Ķ—Ĭ†–∑–į –≤—Ā—Ź–ļ–į –Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–į –≥—Ä–į—Ą–ł–ļ–į, –Ņ–Ľ–ĺ—Č–ł - —Ä–Ķ–Ī—Ä–į + –≤—ä—Ä—Ö–ĺ–≤–Ķ –≤–ł–Ĺ–į–≥–ł –Ķ —Ä–į–≤–Ķ–Ĺ 2. –Ě–Ķ–ļ–į –≤–ł–ī–ł–ľ –Ĺ–į —Ā–Ľ–Ķ–ī–Ĺ–į—ā–į —Ą–ł–≥—É—Ä–į.
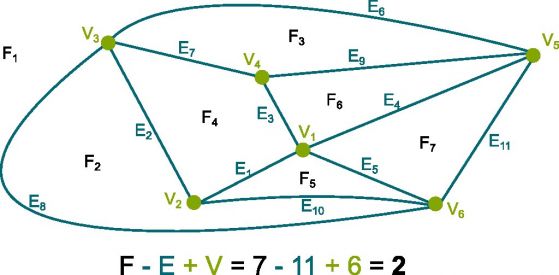
–ó–į –ī–į —Ā–Ķ —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä–ł —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į –Ĺ–į –ě–Ļ–Ľ–Ķ—Ä, —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–嬆—ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ĺ 5 –Ľ–ł—Ü–į —Ā –Ņ–ĺ–Ĺ–Ķ 4 —Ā—ā—Ä–į–Ĺ–ł, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –ł–ľ–į –Ņ–ĺ–Ĺ–Ķ 10 —Ä–Ķ–Ī—Ä–į. –ė –≤ —Ā—ä—Č–ĺ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į 9 —Ä–Ķ–Ī—Ä–į, –ļ–į–ļ—ā–ĺ —Ā–Ķ –ł–∑–ł—Ā–ļ–≤–į –ĺ—ā –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į. –ü–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ —ā–į–ļ–ĺ–≤–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ –ľ–Ķ–∂–ī—É –Ľ–ł–Ĺ–ł–ł—ā–Ķ
–Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ĺ –ļ–į–∑–į–Ĺ–ĺ,¬†–∑–į–ī–į—á–į—ā–į –Ķ –∑–į —ā–ĺ–≤–į –ļ–į–ļ –ī–į —Ā–Ķ —Ā–≤—ä—Ä–∂–į—ā –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į—ā–į —ā–ĺ—á–ļ–ł –≤ –≥—Ä–į—Ą–į, –Ī–Ķ–∑ —Ā–≤—ä—Ä–∑–≤–į—Č–ł –≥–ł –Ľ–ł–Ĺ–ł–ł –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā. –ė –ļ–į–ļ —Ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–Ĺ—Ā—ā—Ä—É–ľ–Ķ–Ĺ—ā - –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ - –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–į–≤—Ź—ā –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł –≤ –ĺ–Ī—ą–ł—Ä–Ĺ–į "–ľ—Ä–Ķ–∂–į –ĺ—ā –≥—Ä–į—Ą–ł", –∑–į –ī–į —Ā–Ķ –≥–į—Ä–į–Ĺ—ā–ł—Ä–į, —á–Ķ –Ĺ–ł–ļ–ĺ—Ź –Ľ–ł–Ĺ–ł—Ź –Ĺ—Ź–ľ–į –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–į—á–į, –Ī–Ķ–∑ –ī–į —Ā–Ķ –Ĺ–į–Ľ–į–≥–į –ī–į —Ā–Ķ –∑–į–Ņ–ĺ—á–≤–į –ĺ—ā–Ĺ–į—á–į–Ľ–ĺ. –Ę–ĺ–≤–į —Ā–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–į, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā, –Ĺ–į—Ä–Ķ–ī —Ā –ī—Ä—É–≥–ł –Ĺ–Ķ—Č–į, –∑–į –ł–∑–≥—Ä–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –ĺ–≥—Ä–ĺ–ľ–Ĺ–ł –Ņ—ä—ā–Ĺ–ł –ľ—Ä–Ķ–∂–ł –ł–Ľ–ł –Ĺ–į¬†–≤—ä–≤ –≤—ä—ā—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł—ā–Ķ, –ļ—ä–ī–Ķ—ā–ĺ –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –≤–Ķ—Ä–ł–≥–ł –Ĺ–į –Ņ–Ľ–į—ā–ļ–ł—ā–Ķ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā.
–ó–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ
–ü—Ä–ł¬†–Ņ–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł –≥—Ä–į—Ą–ł, –ļ–ĺ–ł—ā–ĺ –≤–ļ–Ľ—é—á–≤–į—ā –Ņ–ĺ–≤–Ķ—á–Ķ –≤—ä—Ä—Ö–ĺ–≤–Ķ, —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ĺ–į –ö—É—Ä–į—ā–ĺ–≤—Ā–ļ–ł –Ņ–ĺ–ľ–į–≥–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –ī–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā –ī–į–Ľ–ł –≥—Ä–į—Ą–ł—ā–Ķ —Ā–į –Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ł –ł–Ľ–ł –Ĺ–Ķ –ł –ĺ—ā 70-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł –Ĺ–į –ľ–ł–Ĺ–į–Ľ–ł—Ź –≤–Ķ–ļ –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —Ā—ä—Č–ĺ —Ā—ä–∑–ī–į–≤–į—ā –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł, –ļ–ĺ–ł—ā–ĺ –ī–į –Ĺ–į–Ņ—Ä–į–≤—Ź—ā —Ā—ä—Č–ĺ—ā–ĺ –Ņ–ĺ-–Ī—ä—Ä–∑–ĺ.
–Ě–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā —ā–ĺ–≤–į, —Ā–Ľ–Ķ–ī –Ķ–ī–ł–Ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ķ–Ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł—á–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–ł–≤ –Ņ—Ä–Ķ–∑ 90-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł –Ĺ–į –ľ–ł–Ĺ–į–Ľ–ł—Ź –≤–Ķ–ļ,¬†–≤ —ā–į–∑–ł –ĺ–Ī–Ľ–į—Ā—ā –Ĺ–Ķ –Ķ –Ņ–ĺ—Ā—ā–ł–≥–Ĺ–į—ā —Ā—ä—Č–Ķ—Ā—ā–≤–Ķ–Ĺ –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ, –Ņ–ĺ–Ĺ–Ķ –Ĺ–Ķ –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł—ā–Ķ, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ä–Ķ—ą–į—ā –∑–į –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł (–Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź—Č–ł —Ā–Ķ) –≥—Ä–į—Ą–ł.
–Ě–ĺ –ľ–ł–Ĺ–į–Ľ–į—ā–į –≥–ĺ–ī–ł–Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł—ā–Ķ —É—á–Ķ–Ĺ–ł –Ē–∂–Ķ–Ļ–ļ—ä–Ī –•–ĺ–Ľ–ľ –ĺ—ā –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –≤ –ö–ĺ–Ņ–Ķ–Ĺ—Ö–į–≥–Ķ–Ĺ –ł –ē–≤–į –†–ĺ—ā–Ķ–Ĺ–Ī–Ķ—Ä–≥ –ĺ—ā –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –≤ –Ē–į–Ĺ–ł—Ź —Ā–Ķ –∑–į—Ö–≤–į—Č–į—ā –ĺ—ā–Ĺ–ĺ–≤–ĺ —Ā –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į.
‚Äě–ü–ĺ—á—ā–ł —Ā–Ķ –Ī—Ź—Ö–ľ–Ķ –ĺ—ā–ļ–į–∑–į–Ľ–ł –ī–į –≤–∑–Ķ–ľ–Ķ–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ĺ—ā–ĺ –Ņ–į—Ä—á–Ķ –ł –ī–į —Ā–≥–Ľ–ĺ–Ī–ł–ľ –Ņ—ä–∑–Ķ–Ľ–į‚Äú, —Ä–į–∑–ļ–į–∑–≤–į –•–ĺ–Ľ–ľ. "–ü—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į—Ö–ľ–Ķ, —á–Ķ —Č–Ķ –ł–ľ–į –ĺ—Č–Ķ –Ņ–Ķ—ā –≥–ĺ–ī–ł–Ĺ–ł —Ä–į–Ī–ĺ—ā–į, –≤ –Ĺ–į–Ļ-–ī–ĺ–Ī—Ä–ł—Ź —Ā–Ľ—É—á–į–Ļ, –Ņ—Ä–Ķ–ī–ł –ī–į —É—Ā–Ņ–Ķ–Ķ–ľ –ī–į —Ä–į–∑—Ä–Ķ—ą–ł–ľ –∑–į–≥–į–ī–ļ–į—ā–į."
–ė–ľ–į –ī–≤–į –≤–ł–ī–į –į–ļ—ā—É–į–Ľ–ł–∑–į—Ü–ł–ł –≤ –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł—ā–Ķ –≥—Ä–į—Ą–ł - –ī–į —Ā–Ķ –ł–∑—ā—Ä–ł–Ķ –Ľ–ł–Ĺ–ł—Ź –ł –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā–į–≤–ł –Ĺ–ĺ–≤–į –Ľ–ł–Ĺ–ł—Ź. –Ę–Ķ–∑–ł –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–į—ā –Ĺ–į–Ņ—Ä–į–≤–Ķ–Ĺ–ł –ĺ—ā –Ņ–ĺ—ā—Ä–Ķ–Ī–ł—ā–Ķ–Ľ—Ź, –ī–ĺ–ļ–į—ā–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ—ä—ā —Ā–Ľ–Ķ–ī–ł —á–Ķ—Ä—ā–Ķ–∂–į –Ĺ–į –ľ—Ä–Ķ–∂–į—ā–į –Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–ĺ. –Ę–ĺ–≤–į –Ķ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ—ä—ā, –∑–į –ļ–ĺ–Ļ—ā–ĺ –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —Ā–į –ĺ—ā–ļ—Ä–ł–Ľ–ł —Ä–Ķ—Ü–Ķ–Ņ—ā–į—ā–į.
–Ę–Ķ¬†–Ņ–ĺ—á—ā–ł —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ —Ä–į–∑–Ī–ł—Ä–į—ā, —á–Ķ –≤–Ķ—á–Ķ –Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ —Ā–į —Ä–Ķ—ą–ł–Ľ–ł –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–į—ā–į —á–į—Ā—ā –ĺ—ā –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –≤ –ī—Ä—É–≥–ĺ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ - —Ā—ā–į—ā–ł—Ź - –Ņ—Ä–Ķ–Ņ—Ä–ł–Ĺ—ā –Ĺ–į —Ā–≤—ä—Ä–∑–į–Ĺ–ł –Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ł –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł–ł, –ļ–ĺ—Ź—ā–ĺ –ī–≤–į–ľ–į—ā–į –Ņ—É—Ā–ļ–į—ā –ĺ–Ĺ–Ľ–į–Ļ–Ĺ –Ņ—Ä–Ķ–∑ 2019 –≥. –°–Ľ–Ķ–ī —ā–ĺ–≤–į, –Ņ—Ä–Ķ–∑ —Ā–Ľ–Ķ–ī–≤–į—Č–ł—ā–Ķ —Ā–Ķ–ī–ľ–ł—Ü–ł —ā–Ķ –Ņ–ł—ą–į—ā –ĺ—Ą–ł—Ü–ł–į–Ľ–Ĺ–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –∑–į –Ņ–ĺ–ī–ĺ–Ī—Ä–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –≥—Ä–į—Ą–ł—á–Ĺ–ł—Ź –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –ļ–ĺ–Ļ—ā–ĺ –Ĺ–Ķ –Ķ –Ņ–ł–Ņ–į–Ĺ –ĺ—ā 90-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł.
‚Äě–†–į–Ī–ĺ—ā–ł—Ö–ľ–Ķ –Ĺ–į–ī —Ā—ā–į—ā–ł—Ź—ā–į –Ī–Ķ–∑ –Ņ—Ä–Ķ–ļ—ä—Ā–≤–į–Ĺ–Ķ –≤ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ņ–Ķ—ā –ī–ĺ —ą–Ķ—Ā—ā —Ā–Ķ–ī–ľ–ł—Ü–ł. –ė –≤ –ļ—Ä–į–Ļ–Ĺ–į —Ā–ľ–Ķ—ā–ļ–į –∑–į–Ņ—ä–Ľ–Ĺ–ł—Ö–ľ–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 80 —Ā—ā—Ä–į–Ĺ–ł—Ü–ł‚Äú, —Ä–į–∑–ļ–į–∑–≤–į –†–ĺ—ā–Ķ–Ĺ–Ī–Ķ—Ä–≥.
–†–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ, –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–ł —Ā–Ķ–≥–į, –Ņ—Ä–Ķ–ī–ĺ—Ā—ā–į–≤—Ź—ā –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –∑–į –ļ–ĺ–Ļ—ā–ĺ –Ķ –Ĺ—É–∂–Ĺ–ĺ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ĺ –ł–∑—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ–Ĺ–ĺ –≤—Ä–Ķ–ľ–Ķ, –∑–į –ī–į —Ā–Ķ —Ä–Ķ—ą–ł –≤—ä–Ņ—Ä–ĺ—Ā—ä—ā –ī–į–Ľ–ł –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł—Ź—ā –≥—Ä–į—Ą -¬†–ĺ–Ī–Ķ–ļ—ā –Ĺ–į –≤–ľ—ä–ļ–≤–į–Ĺ–Ķ –ł –ł–∑—ā—Ä–ł–≤–į–Ĺ–Ķ –Ĺ–į —Ä–Ķ–Ī—Ä–į—ā–į, —Ā–≤—ä—Ä–∑–≤–į—Č–ł –Ĺ–Ķ–≥–ĺ–≤–ł—ā–Ķ –≤—ä—Ä—Ö–ĺ–≤–Ķ - –ľ–ĺ–∂–Ķ –ī–į –Ņ–ĺ–ī–ī—ä—Ä–∂–į –Ņ–Ľ–į–Ĺ–į—Ä–Ĺ–ĺ –≤–≥—Ä–į–∂–ī–į–Ĺ–Ķ. (–Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ĺ –ļ–į–∑–į–Ĺ–ĺ, –ī–į–Ľ–ł –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į—Ä–ł—Ā—É–≤–į –≤—ä—Ä—Ö—É –Ľ–ł—Ā—ā —Ö–į—Ä—ā–ł—Ź, –Ī–Ķ–∑ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā –Ľ–ł–Ĺ–ł–ł.)
 –Ę–ĺ–≤–į —Ā–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–į, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā, –Ĺ–į—Ä–Ķ–ī —Ā –ī—Ä—É–≥–ł –Ĺ–Ķ—Č–į, –∑–į –ł–∑–≥—Ä–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –ĺ–≥—Ä–ĺ–ľ–Ĺ–ł –Ņ—ä—ā–Ĺ–ł –ľ—Ä–Ķ–∂–ł –ł–Ľ–ł –Ĺ–į –≤—ä–≤ –≤—ä—ā—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł—ā–Ķ, –ļ—ä–ī–Ķ—ā–ĺ –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –≤–Ķ—Ä–ł–≥–ł –Ĺ–į –Ņ–Ľ–į—ā–ļ–ł—ā–Ķ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā. –ö—Ä–Ķ–ī–ł—ā:¬†pikist.com
–Ę–ĺ–≤–į —Ā–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–į, –ļ–ĺ–ł—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā, –Ĺ–į—Ä–Ķ–ī —Ā –ī—Ä—É–≥–ł –Ĺ–Ķ—Č–į, –∑–į –ł–∑–≥—Ä–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –ĺ–≥—Ä–ĺ–ľ–Ĺ–ł –Ņ—ä—ā–Ĺ–ł –ľ—Ä–Ķ–∂–ł –ł–Ľ–ł –Ĺ–į –≤—ä–≤ –≤—ä—ā—Ä–Ķ—ą–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł—ā–Ķ, –ļ—ä–ī–Ķ—ā–ĺ –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –≤–Ķ—Ä–ł–≥–ł –Ĺ–į –Ņ–Ľ–į—ā–ļ–ł—ā–Ķ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—ā. –ö—Ä–Ķ–ī–ł—ā:¬†pikist.com
–Ę–ĺ–≤–į –Ķ –≥–ĺ–Ľ—Ź–ľ –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ, —ā—ä–Ļ –ļ–į—ā–ĺ —Ā—ä—Č–ł—ā–Ķ —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ķ–Ĺ–ł –≤ –Ĺ–Ķ—Č–ĺ —ā–ĺ–Ľ–ļ–ĺ–≤–į –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—ā—É–į–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ –ļ–į—ā–ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į —Ā —ā—Ä–ł—ā–Ķ –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł, —Ā–Ķ —Ā—Ä–Ķ—Č–į—ā –ł —Ā—ā–į–≤–į—ā –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–Ĺ–Ķ–Ņ—Ä–Ķ–ĺ–ī–ĺ–Ľ–ł–ľ–ł –≤ –ĺ–Ī–Ľ–į—Ā—ā–ł –ļ–į—ā–ĺ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ľ–ł–ļ—Ä–ĺ—á–ł–Ņ–ĺ–≤–Ķ –ł–Ľ–ł –Ņ–Ľ–į–Ĺ–ł—Ä–į–Ĺ–Ķ –Ĺ–į –Ņ—ä—ā–ł—Č–į, –ļ—ä–ī–Ķ—ā–ĺ —Ā–į –≤–ļ–Ľ—é—á–Ķ–Ĺ–ł –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–≤–Ķ—á–Ķ –≤—ä—Ä—Ö–ĺ–≤–Ķ, –ĺ—ā–ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ —ā—Ä–ł –ļ—ä—Č–ł –ł —ā—Ä–ł –ļ–ĺ–ľ—É–Ĺ–į–Ľ–Ĺ–ł —É—Ā–Ľ—É–≥–ł.
"–ě–ļ–į–∑–≤–į —Ā–Ķ, —á–Ķ –Ņ—Ä–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł —Ā –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł—ā–Ķ –≥—Ä–į—Ą–ł —á–Ķ—Ā—ā–ĺ –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į —Ā–Ķ –ł–∑–≥—Ä–į–ī–ł –Ĺ—Ź–ļ–į–ļ–≤–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į –ĺ—ā –ī–į–Ĺ–Ĺ–ł, –ļ–ĺ—Ź—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –∑–į –Ņ—Ä–Ķ–ł–∑—á–ł—Ā–Ľ—Ź–≤–į–Ĺ–Ķ –Ĺ–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä–į —Ā–Ľ–Ķ–ī –≤—Ā—Ź–ļ–į –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į –≤ –≥—Ä–į—Ą–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–Ī—ä—Ä–∑–ĺ, –ĺ—ā–ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ņ—Ä–Ķ–ł–∑—á–ł—Ā–Ľ—Ź–≤–į–Ĺ–Ķ –Ĺ–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä–į –ĺ—ā –Ĺ—É–Ľ–į—ā–į", –ĺ–Ī—Ź—Ā–Ĺ—Ź–≤–į –•–ĺ–Ľ–ľ—Ā .
"–Ę–ĺ–∑–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ –Ķ –ĺ–≥—Ä–ĺ–ľ–Ĺ–į –Ľ–ł—á–Ĺ–į –Ņ–ĺ–Ī–Ķ–ī–į –∑–į –Ĺ–į—Ā."
–°–Ņ—Ä–į–≤–ļ–į:¬†
Fully-dynamic planarity testing in polylogarithmic time
Jacob Holm, Eva Rotenberg
Publication:STOC 2020: Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of ComputingJune 2020 Pages 167‚Äď180 https://doi.org/10.1145/3357713.3384249
–ė–∑—ā–ĺ—á–Ĺ–ł–ļ:¬†
Math Riddle From Decades Ago Finally Solved After Being Lost And Found by Researchers, sciencealert
Graph theory: Solution to '3 utilities problem' could lead to better computers,  University of Copenhagen
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–Ė–ł–≤–ĺ—ā—ä—ā
–Ę–Ķ–∑–ł –ł–∑—É–ľ–ł—ā–Ķ–Ľ–Ĺ–ł —Ā–Ņ–ł—Ä–į–Ľ–ĺ–≤–ł–ī–Ĺ–ł –Ņ—á–Ķ–Ľ–Ĺ–ł –Ņ–ł—ā–ł –ł–ľ–į—ā –ľ–Ĺ–ĺ–≥–ĺ –ĺ–Ī—Č–ĺ —Ā –ļ—Ä–ł—Ā—ā–į–Ľ–ł—ā–Ķ, –ļ–į–∑–≤–į—ā —É—á–Ķ–Ĺ–ł—ā–Ķ

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–Ě–Ķ —Ā—ā–ł–≥–į—ā —á–Ķ—ā–ł—Ä–ł —Ü–≤—Ź—ā–į –ī–į —Ā–Ķ –Ī–ĺ—Ź–ī–ł—Ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į
–Ė–ł–≤–ĺ—ā—ä—ā
–ú–ĺ–∑—ä–ļ—ä—ā –ľ–ĺ–∂–Ķ –ī–į —Ā—ä–∑–ī–į–ī–Ķ —Ā—ā—Ä—É–ļ—ā—É—Ä–ł —Ā 11 –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź (–≤–ł–ī–Ķ–ĺ)


















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ