Непериодичните подреждания, при които отделните елементи могат да плътно да пасват помежду си, създавайки безкрайни модели или патерни, които никога не се повтарят, вълнуват математиците от десетилетия, но досега никой не знаеше дали това може да стане само с една фигура.
Математиците са открили една единствена форма, която може да се използва за пълно покриване на повърхност, без да се създава повтарящ се модел. Дълго търсената форма е изненадващо проста, но откриването ѝ е отнело десетилетия - и би могла да намери приложение във всичко - от материалознанието до дизайна.
Обикновени форми като квадрати и равностранни триъгълници могат да покриват повърхност с плочки или плътно да я покриват без пропуски в повтарящ се модел, който е познат на всеки, който се е взирал в стената на банята.
Но Дейвид Смит, Джоузеф Самуел Майерс, Крейг С. Каплан и Хаим Гудман-Щраус са създали една-единствена форма, която запълва равнината и не може да бъде подредена с транслационна симетрия.
Това вероятно е най-голямата математическа новина, отнасяща се за непериодичните мозайки.
И изглежда толкова просто!
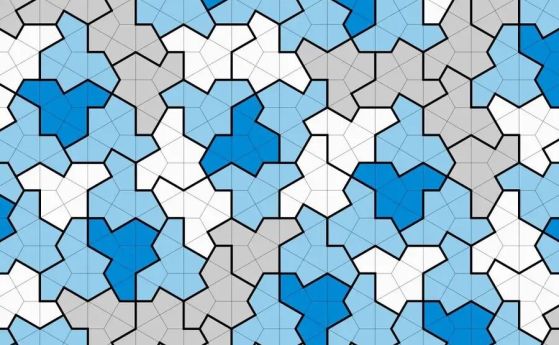
Непериодичната фигура „шапка“. Кредит: D. Smith et al/arXiv.org 2023
Геометрите са търсили форма с тези свойства в продължение на повече от 60 години и докато този пример не бе открит, не бе ясно дали такава изобщо съществува.
Плочката е направена от осем хвърчила – формата, която се получава като изрежете шестоъгълник през средните точки на ръбовете му.
Кредит: D. Smith et al/arXiv.org 2023
Всъщност те показват, че има цяло непрекъснато семейство от непериодични плочки, получени чрез промяна на дължините на ръбовете във формата, показана по-горе. Ето една анимация от Крейг Каплан, показваща непрекъсната трансформация в цялото семейство:
Обърнете внимание, че има три точки в анимацията, където формата е изродена (в началото, средата и края), тъй като два съседни ръба стават успоредни и тези форми могат да се подреждат периодично.
Авторите са създали сайт, който да придружава статията им, доказвайки, че формата е непериодична фигура. Прочетете статията: тя е наистина добре написана и започва с подробно въведение, описващо проблема и неговата история.
Има и интерактивен инструмент за създаване на кръпки от облицовката: избирате с кой от основните клъстери H, T, P или F искате да започнете и след това щракнете върху Build Supertiles („Изграждане на суперплочки“), за да приложите процеса на заместване и да завършите с по-голям кръпка от плочки.
Струва си да се отбележи, че това е само предпечат, така че може да се открие грешка в доказателството, но това съобщение е достоверно: авторите са добре известни математици, които работят по този и подобни проблеми от дълго време, и схемата на доказателството изглежда последователна.
Авторите наричат формата си „шапката на Айнщайн“, каламбур на немското „ein“ – един, „stein“ – камък (или плочка).
Формата има 13 страни и екипът я нарича просто „шапката“, защото им напомня на шапка.
Дейвид Смит е публикувал "алтернативен лексикон" в блога си, в който дава част от историята за това как са замислени формите. Дейвид отбелязва, че всъщност са открили две фигури: „шапката“ отгоре и фигура, направена от 10 хвърчила, която прилича на костенурка:
Защрихованите области по-долу показват приликите между двете плочки. Шапката е съставена от 8 хвърчила, а костенурката от 10.
Шапката (вляво) и костенурката (вдясно). Кредит: D. Smith et al/arXiv.org 2023
Периодични и непериодични мозайки
Представете си 2D равнина – безкрайна плоска повърхност. Как може да я покриете напълно? Ако имате безкраен запас от плочки, можете ли да ги подредите плътно в равнината, така че да няма празнини?
Задачата е по-интересна, ако се ограничите до определен, краен набор от различни форми на плочки, а не с произволна форма.
Подреждане на равнината с квадрати, триъгълници и комбинация от триъгълници и шестоъгълници.
Можете да направите това с безкрайно много квадрати с еднакъв размер или с комбинация от равностранни триъгълници и правилни шестоъгълници. Ако всичко, което имате, са правилни петоъгълници, не можете да го направите: без значение как ги подреждате, в крайна сметка ще се окажете с празнина, която е твърде малка, за да поставите петоъгълна плочка.
Петоъгълниците не облицоват равнината
Следващият въпрос е: след като поставите плочките, има ли симетрии? Ако току-що сте използвали квадрати, тогава можете да преместите всяка плочка с едно място надолу и тя ще изглежда точно както преди.
 |
Облицовката с квадрати има транслационна симетрия
Възможно ли е да подредите плочките така, че да няма транслационна симетрия – така че всяка точка в равнината да изглежда напълно уникална? Това се нарича непериодично подреждане.
Ако разделите квадрат на няколко правоъгълника с еднакви пропорции, можете да създадете непериодично подреждане на равнината, като ги подредите в различна конфигурация в зависимост от позицията им в равнината. Но можете също така да ги подредите по един и същи начин навсякъде, така че ще има транслационна симетрия.
Интересният въпрос е: има ли някакви плочки или набори от плочки, които могат да покрият равнината, но никога с транслационна симетрия – истински непериодични плочки?
Роджър Пенроуз е открил двойка форми – хвърчило и стреличка, със специфични дължини на ръбовете или алтернативно двойка ромби, маркирани така, че да се подчиняват на определени правила за съпоставяне на ръбовете – които заедно запълват равнината, но никога не могат да произведат транслационна симетрия.
Облицовка на Пенроуз с ромбове. Кредит: Wikimedia Commons
Това, което никой не знаеше досега, беше дали има единична форма на плочка, която генерира само непериодични мозайки.
Именно това са установили Смит, Майерс, Каплан и Гудман-Строс.
Те откриват фигурата, като първо ограничават възможните варианти с помощта на компютър и след това проучват получените по-малки комплекти на ръка. След като получават това, което смятаха за добра възможност, те го тестват с помощта на комбинаторна софтуерна програма.
Те доказват, че плочката покрива равнината, което е по-лесната част, а след това доказват, че тя покрива равнината непериодично. Те са измислили нова техника за доказване на това - всъщност две: доказали са го два пъти, за да са сигурни.
Това е кратката версия на историята.
Как работи доказателството за непериодичност
Няма как шапката да се подреди периодично. Кредит: D. Smith et al/arXiv.org 2023
Авторите показват, че без значение как поставяте плочките, винаги ще бъде възможно да ги разделите, така че всяка плочка да принадлежи към един от набор от четири клъстери – специфични подредби от 1, 2 или 4 плочки – и че ръбовете на съседни клъстери могат да съвпадат само по определени начини.
Четирите групи от единична форма на плочка, която генерира само непериодични мозайки. Кредит: D. Smith et al/arXiv.org 2023
Тази част от доказателството е направена с помощта на компютър: има много случаи и е вероятно да допуснете грешка, докато се опитвате да ги изведете на хартия, затова вместо това авторите разчитат да проверят дали кодът на тяхната програма за проверка е правилен.
След това те показват, че тези клъстери сами по себе си винаги могат да бъдат разделени на по-големи групи, наречени метаплочки, които имат същите симетрии като основните плочки. Така че, ако мозайката, разглеждана като съвкупност от единични плочки, има транслационна симетрия, то ако я разглеждаме като съвкупност от метаплочки, тя също трябва да има тази симетрия.
И след това те показват, че плочката от метаплочки не може да има транслационна симетрия! Така че и облицовката с моноплочки не го прави.
Четирите форми на метаплочки. Четири многоъгълника, обозначени с Т, Н, П и Е. Всеки от периметрите им е разделен на оцветени и анотирани участъци, съответстващи на правилата за съвпадение. Кредит: D. Smith et al/arXiv.org 2023
За да покажат, че плочката от метаплочки е непериодична, те просто правят същия трик отново, безкрайно: показват, че метаплочките образуват клъстери и след няколко стъпки клъстерите от една стъпка изглеждат същите като клъстерите от предишната стъпка, само че по-големи. Тези самоподобни форми се наричат суперплочки.
След като идентифицирате суперплочките, може да извършите заместване, за да получите следващата стъпка от процеса на клъстериране.
Участък от плочките с наложени няколко слоя суперплочки. Кредит: D. Smith et al/arXiv.org 2023
Второто доказателство се основава на факта, че шапката е част от континуум от форми: чрез постепенна промяна на относителните дължини на страните на шапката, математиците са успели да формират семейство от плочки, които могат да приемат един и същ неповтарящ се модел.
Спомнете си, че предположихме, че вече разглеждате пълна мозайка на равнината и сте намерили участък от съседни суперплочи. Заменете всяка суперплочка с определена подредба на копия на четирите възможни суперплочки и по-големият участък от плочки, което ще получите, трябва да съвпада точно с подредбата, която сте получили, покривайки по-голяма част от равнината, отколкото участъка, който сте започнали да разглеждате.
Кредит: D. Smith et al/arXiv.org 2023
Тъй като няма транслационна симетрия вътре в суперплочките, тогава няма транслационна симетрия между метаплочките, а оттам и оригиналните плочки.
Реакции
The new aperiodic monotile discovered by Dave Smith, Joseph Myers, Craig Kaplan, and Chaim Goodman-Strauss, rendered as shirts and hats. The hat tiles are mirrored relative to the shirt tiles. pic.twitter.com/BwuLUPVT5a
— Robert Fathauer (@RobFathauerArt) March 21, 2023
Формата е много лесна за правене. В GitHub има хранилище на файлове, представящи формата в различни формати, за използване в графичен дизайн или 3D печат.
Дан Пайкър добавя линии тип Труше на плочката, за да направи този хубав патерн:
Дейв Ричесън е отпечатал плочката на своя 3D принтер и е поставил своя моделен файл в Thingiverse за всеки друг, който иска да я отпечата.
Травис Хауз прескача едно измерение и използва своя лазерен нож, за да произведе набор от плочки:
Адам Гаучер е писал в блога си за статията, отбелязвайки, че съотношението на обърнатите плочки към необърнатите плочки е
Справка: David Smith et al, An aperiodic monotile, arXiv (2023). DOI: 10.48550/arxiv.2303.10798
Източници:
A geometric shape that does not repeat itself when tiled, Bob Yirka, Phys.org
An aperiodic monotile exists!, Christian Lawson-Perfect, Katie Steckles and Peter Rowlett, Аperiodical
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари