
В чест на юбилея на колонката Monday Puzzle на Guardian, изданието представя сингапурска математическа задачка, която доби голяма популярност.
В средата на май посетителите на интернет бяха развълнувани от задача, която уж се дава за решаване от първокласници в Сингапур, а това са деца на възраст от 5 до 7 години, и която се оказва толкова сложна, че никой не можа да я реши.
Но нашата история не е за това, как фрази като "математическа задача взриви интернет" са вече досадни и предвидими опити за привличане на посетители към даден сайт.

Внимателно прегледайте последователността от числата и попълнете празните кръгчета.
Дори един кратък поглед на тази задача, която за пръв път се появява в технически форум в Сингапур, позволява да се види, че тази снимка е очевидно фалшива. Снимката изглежда манипулирана, а към задачата липсват всякакви пояснения.
Задачата е видоизменена в сайта, воден от Гордън Бъргин (Gordon Burgin), американски пенсиониран учител. Във версията на задачата от неговия сайт в долната лява четвъртинка е числото 20. В сингапурската снимка 0-та е замазана. Не е изненадващо, че няма очевидно решение.
"Аз съм поразен от този фалшикат и не знам какво са се опитвали да постигнат с това", коментира Бъргин. - "Ако целта им е била бурна дискусия и последващо отчаяние, те са я постигнали".
Следва правилната версия на загадката.
1. Във всеки от четирите сектора на външния кръг има двуцифрено число, равно на сумата от трите числа, разположени в ъглите на сектора. Числата в кръгчетата могат да приемат стойности от 1 до 9 и всяко от числата може да се използва само веднъж. Едно от числата е дадено, за да започнем. Намерете останалите четири.
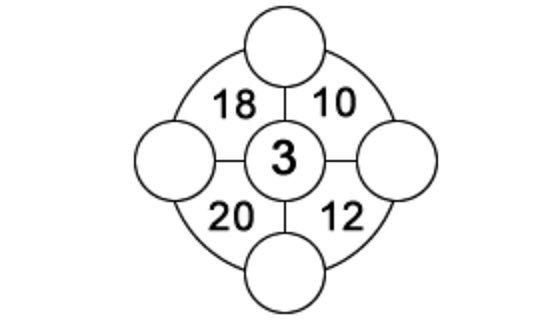
2. Следващата задача е да се превърне версията от Сингапур (със затритата нула) в смислен въпрос.
Тази загадка напомня задачка от една от най-интересните книги, посветени на историята на загадките - "Wakoku chiekurabe", стара японска книга за загадки, публикувана през 1727 година.
3. Запишете числата от 1 до 9 в черните кръгчета така, че сумата от числата във всеки от двата сини кръга (включително централния кръг), а също по хоризонталните и вертикалните линии, да е една и съща.

Тези четири суми, всяка от които се състои от пет събираеми, както и всички суми, трябва да са равни.
Ето една илюстрация от самата книга, която показва подобна задача.

Решенията

Това са някои от решенията и вариантите на сингапурската задача, пристигнали в редакцията на The Guardian:
1. По часовата стрелка, започвайки отгоре: 6, 1, 8, 9

Ако наречем позициите на числата Север, Изток, Запад и Юг, то кандидати за Запад и Юг ще бъдат 8 и 9, тъй като Ю + З + 3 = 20, или Ю + З = 17. Но ние знаем, че Ю + И + 3 = 12, или Ю + И = 9. Но Ю не може да бъде 9, защото тогава И = 0, а това не е разрешено в условието. Следователно Ю = 8, З = 9, С = 6 и И = 1.
2. Ето един интересен вариант на задачата от читател на име Том Фланъри (Tom Flannery).
Попълнете кръгчетата с цели числа така, че сумата от секторите във всяка полукръжност да е равна на сумата от числата в кръгчетата.
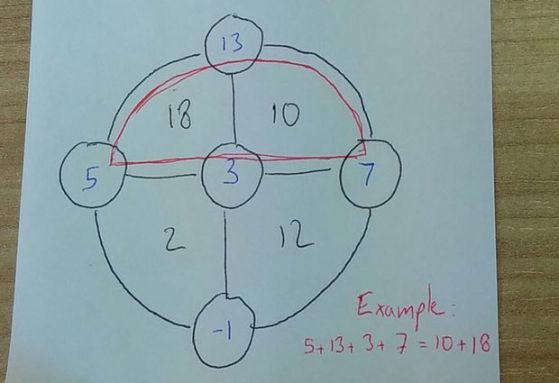
3. И едно решение на последната задача от японския сборник със загадки от 1727 година.
Запишете числата от 1 до 9 в черните кръгчета така, че сумата от числата във всеки от двата сини кръга (включително централния кръг), а също по хоризонталните и вертикалните линии е една и съща.

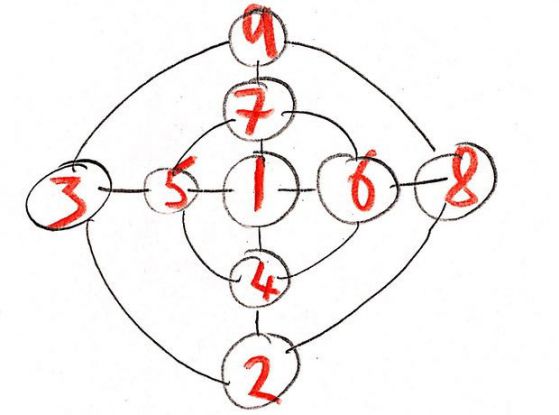
Ключът за решаването е да е разбере, че в центъра могат да бъдат само нечетни числа или по-точно могат да са 1, 3, 5 или 9,
След като сте избрали числото за центъра, разделете останалите числа на двойки, чиято сума дава едно и също число и поставете тези двойки в противоположни кръгчета. Ако изберете 1, както е в случая, получаваме двойките 2 и 9; 3 и 8; 4 и 7; и 5 и 6, като сумата на всяка двойка е 11. Разпределете позициите на двойките и готово!
Ето още едно решение, изпратено от Франциско Сампейа (Francisco Zampella): числа хоризонтално: 9-5-3-6-1. вертикална: 7-8-3-2-4.























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews