Задача: Да подредим еднакви тела най-далеч от ръба

През ноември списание Quanta изправи читателите си пред предизвикателството да подредят идентични плоски предмети (като монети или плочки), по един на ниво, така че да се надвесят извън ръба на масата, колкото се може по-далеч.

Математиката зад тази задача е проста и елегантна и решихме да я споделим с вас.

Вопрос 1

В класическата задача за построяването на надвиснали фигури всички блокове трябва да бъдат еднакви по размер и форма, а тяхната дължина се приема за единица. На всяко ниво на фигурата може да има само един блок. Блоковете не може да се слепват. Ако имате пет такива блокове, на каква максималната дължина може да стърчи краят на най-горния блок от ръба на масата, на която лежат блоковете? Можете ли  да изведете формула за максималното надвисване за n блокове?

Физическият принцип изисква да се балансира въртящият момент (или моменти) от двете страни на ръба на масата. Въртящият момент за всеки елемент се намира като се умножи масата на този елемент и разстоянието от неговия масов център до ръба.

Въпреки, че по-коректно е да използваме параметъра "маса", за по-голяма яснота ще използваме теглото на елементите, а и резултатът ще е един й същ, защото теглото се получава като масата се умножи по земното ускорение, което е приблизително g=9.81 м/сек и е константа в тази задача.

Когато центърът на тежестта е точно над ръба и двете страни имат равни въртящи се моменти и общият въртящ се момент за ръба е нула. За обект, който е съставен от много елементи, общият въртящ се момент може да бъде намерен като се съберат моментите на всички съставни части със съответния знак спрямо посоката на въртене. Това ни позволява да разделим проблема по прост начин, като вземаме предвид само промените, които стават, когато добавим един нов блок към съществуващата конструкция, по начин, подобен на математическата индукция - може да го приемем за физическа индукция.

Да разгледаме стълб от n-1 блокове, всеки с маса (тегло) единица и с дължина единица, точно балансиран на ръба на масата. Представете си, че линията на очите е точно по ръба на масата и масата е вляво, а надвисналите краища на блоковете са вдясно. Тъй като стълбът е точно балансиран, центърът на тежестта е точно над ръба и цялата купчина има въртящ се момент нула спрямо ръба. Сега да се представим, че повдигаме целия стълб нагоре и поставяме друг блок под нея, така че десния ръб на този блок да се подравнява с ръба на масата. Това може да бъде трудно да се направи на практика, но в мисловен експеримент е лесно.

Ние добавяме още стабилност на купчината, защото добавяйки n-тия блок на дъното, центърът на тежестта на стълба малко се премества вляво. Нека наречем това разстояние х.

n блокове, тежащи n единици, сега имат общ въртящ се момент х*п за ръба на масата и насочен на ляво. Да си припомним, че стълбът от n-1 блокове има общ въртящ се момент нула. Добавихме само един блок с единица тегло и с разстояние до центъра на тежестта половин единица от ръба на масата.

Получава се, че x*n = 1/2, което значи, че x = 1/2n, където x е разстоянието до новия център на тежестта от ръба на масата.

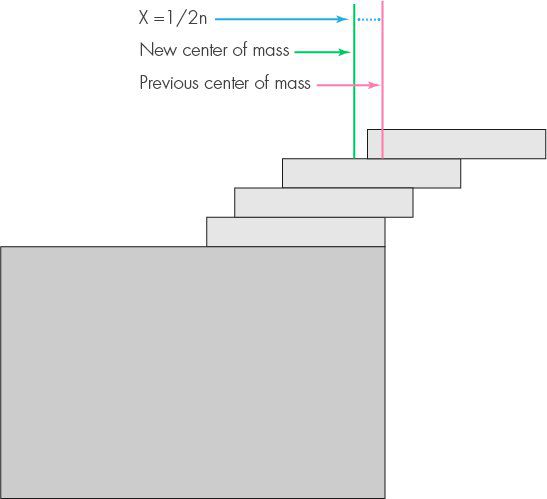
Това означава, че ако се премести цялата група от n блокове надясно с дължина 1/2n, тя ще бъде перфектно балансирана на ръба - и че това е максималната възможното преместване. За да завършим изграждането на индукцията, отбелязваме, че максимално стърчащият край на първия блок от ръба на масата е 1/2 от дължината на блока.

За 5 блока можем да заменим във формулата n са всяко ниво от 1 до 5, за да получим максималното надвесване:

$// <![CDATA[ x = \frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\frac{1}{10}= \frac{137}{120}= 1.141\bar{6} // ]]>$

Вижда се, че ако започнем от върха и след това се добавят блокове надолу всяка промяна ще бъде половината от обратното количество на наличните блокове. Такава последователност от обратни числа, известна като хармоничен ред. Такъв ред е бавно разходящ, а когато n се стреми към безкрайност, също клони към безкрайност.

Общата формула за сумата от п блокове се получава чрез сумиране на всички членове на реда.  Получава се половината от n-тия хармоничен член, който може да се запише като:

$// <![CDATA[ H_{n}= \sum_{k=1}^{n}\frac{1}{k} // ]]>$

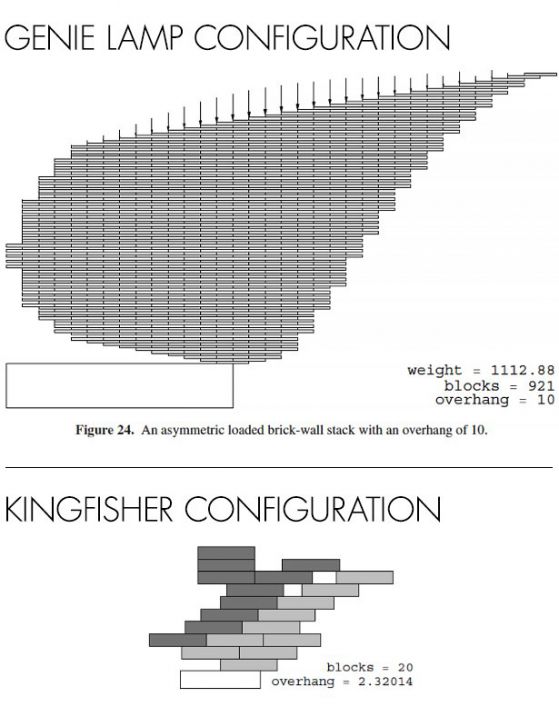
Може да се постигне най-голям надвес, ако се допусне използването на няколко блокове на едно ниво. Оптималното решение на тази задача е описано в публикация от 2009 година "Максимален надвес" [Maximum Overhang, by Paterson, Peres, Thorup, Winker and Zwick]. Според автора на статията в списание Quanta Pradeep Mutalik тези малки проекти, направени от техника на Патерсън-Звика напомнят по форма на птичето земеродно рибарче. По-големите изглеждат като вълшебната лампа на Аладин. За надвес от две дължини тези схеми са 2 - 3 пъти по-ефективни, отколкото класическите хармонични надвисвания и такива надвеси се достигат с помощта на 14 блока, вместо 32. За съжаление тяхната математика е твърде сложна, но можем да се насладим поне на изгледа им.

Още по темата

22/11/2015

Математика

Хипотезата на Риман за лаици