
Топологична размерност
През 300 г. до н. е. Евклид започнал първата книга на "Начала" с няколко определения, които били:
- Точка е това, което няма части.
- Линията е дължина без ширина.
- Повърхност е това, което има само дължина и ширина.
В Книга XI, добавил:
Обемна фигура е това, което има дължина, ширина и височина.
В тези определения се очертава понятието размерност. Всеки знае, че точката има нулева размерност, линията има размерност 1, квадратът е двуизмерен, а кубът - триизмерен.
Интуитивно ние разбираме термина размерност като броя на координатите, необходими за определяне на местоположението на точка във вътрешността на формата. По този начин, всяка една линия - права, крива, отворена или затворена (например, окръжност) е едномерна - достатъчна е само една координата за да се покаже къде точно е точката. Равнините и кривите повърхности като повърхността на сфера например, са двуизмерни по същата логика. Положението на точка от повърхност, ограничена от квадрат може да се зададе с две стойности и тогава размерността й ще бъде равна на две.
Тази размерност се нарича топологична. Тя се е използвала в течение на хилядолетия, но се оказва недостатъчна при изучаването на фракталите.
Дробната размерност
Размерността зависи силно от това как се мери в изследвания обект. Един квадрат има две измерения, но ако си представим, че е запълнен със силно нагънато въже, получаваме нещо като крива на Пеано.
 |
Да разгледаме една от кривите на Пеано, фрактал наречен "Гръцки кръст".
Той се чертае по следните правила:
|
|
Първият етап е отсечка. После тя се заменя с 9 отсечки с дължина 3 пъти по-малка от дължината на първоначалната отсечка (1 и 2 на схемата долу). След това, всяка от отсечките се заменя със същата тази фигура и повтаряйки този процес безкрайно, ще се получи плътен квадрат. Минете с мишката върху цифрите долу за да видите този процес. |
 |
|||||
| Цикли: | 1 | 2 | 3 | 4 | 5 | 6 |
Усетихте ли какъв е проблема? Фракталът се състои от отсечки, на които топологичната размерност е 1. Това обаче не е вярно, защото получената фигура - квадрат е с размерност 2.
Може да се докаже, че за всяка точка от този квадрат може да се намери точка, принадлежаща към кривата на Пеано.
Кривите на Пеано и Прахът на Кантор не са "нормални" геометрични обекти. Тяхната размерност не е равна на топологичната. Прахът на Кантор изглежда построен от едномерна линия, но се състои от точки с размерност 0, а кривата на Пеано е построена на базата на едномерна линия, а резултатът е повърхност.
Топологичната размерност на линия може да е 1, а на повърхността – 2, но при фрактала това значение на размерността може да бъде между 1 и 2 или между 2 и 3. Фракталите могат да имат и цели стойности размерност, но тя винаги е по-голяма от топологичната..
Фракталът срещу геополитиката
 |
рамка 1 |
| приближение 1 | |
| рамка 2 | |
| приближение 2 | |
| рамка 3 | |
| приближение 3 | |
| рамка 4 | |
| приближение 4 |
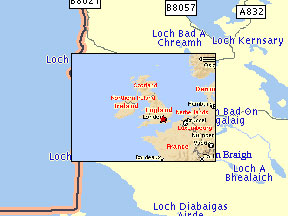
По време на Втората световна война английският математик Люис Фрай Ричардсън бил осенен от оригинална идея. Той предположил, че агресивността на една държава или империя зависи от дължината на нейната граница. Според него вероятността за война между две съседни държави зависи от дължината на границата, която ги разделя. Започнал да събира данни, но се натъкнал на парадокса, че в различните справочници дължините на бреговата линия например на Англия се различавала с 20-30%, дори и 2 пъти. Затова Ричардсън решил да измери сам дължината на брега на Англия. Но скоро разбрал, че колкото по-подробни карти използвал, толкова по-дълга ставала измерената бреговата линия.
Ричардсън установил, че нарастването става по добре изразен степенен закон. Той е съпоставил стъпката на измерване и получената дължина и намерил добре изразени линейни зависимости в логаритмични координати. Изразени графично, техният наклон бил мярка за това колко е ерозирал (насечен, назъбен) брега.
Ако някой реши да продължи упорито задачата на Ричардсън и отиде на място, в Англия и с дърводелски метър измери бреговата й линия, тази дължина ще бъде още по-голяма от измерените по карта. Може да се продължи този процес още, докато с подходящ уред не се стигне до песъчинките, до атомите или до дължината на Планк. Задачата е непосилна.
Манделброт е използвал този пример за да покаже, че бреговата линия на Англия всъщност има безкрайна дължина, тя е фрактал и определил, че фракталната му размерност е 1.25.
Как да пресметнем размерността на фрактал
Метод на подобието
Това е най-простият метод за изчисляване размерността на фрактал, който използва свойството самоподобие.
| Например, да вземем отсечка с размерност 1. Ако я разгледаме с увеличение 2 пъти, ще видим 2 идентични отсечки. Нека да използваме променливата D за размерност (означава степента на увеличение) и N за количеството идентични фигури. |  |
|
| Ако разгледаме квадрат и триъгълник с размерност 2. С увеличение 2, получаваме 4 идентични фигури и в двата случая. |  |
|
| Ако увеличим 2 пъти куб с размерност 3, получаваме 8 идентични кубове. В тези три примера, се забелязва ясна закономерност. |  |
|
Ако повдигнем увеличението e на степен размерността D, винаги ще получаваме количеството фигури N:
eD = N
Така с помощта на тази формула можем да изчисляваме размерността D:
D = log N / log e
Логаритъмът е степента D, на която трябва да бъде повдигната основата e, за да се получи числото N. Основата може да е кое да е положително число, различно от единица. Тук е записан логаритъм с основа 10, но в много източници, формулата е записана с естествен логаритъм ln с основа числото е=2.718, наричан е още неперов логаритъм, а числото e - неперово число
|
Да разгледаме друг фрактал, кривата на Кох, описана от Нилс Фабиан Хелге фон Кох (Niels Fabian Helge von Koch) през 1906г. В този фрактал се виждат четири идентични снежинки (N = 4). Всяка от тях е 1/3 от всяка фигура, така че e = 3. За изчисление на фракталната размерност: D = log 4 / log 3 =1.26. Според изчисленията на Беноа Манделброт, брегът на Англия има близка ( 1.25) размерност с размерността на кривата на Кох. |
 |
|
|
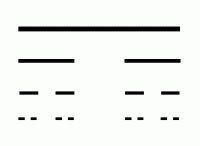
При т.н. Прах на Кантор първоначалната отсечка, се дели на 3 (e = 3), отстранява се вътрешна 1/3 част и след операцията остават 2 отсечки (N = 2), общата дължината на отсечките клони към нула. Фракталната размерност е : D = log 2 / log 3 =0.631. |
 |
|
Геометричен метод
Методът на подобие за изчисление на фракталната размерност е много ефективен, ако имаме работа с фрактали съставени от определено количество идентични версии на самите себе си. Но опитайте да го приложите за крайбрежието на Англия. Това е невъзможно, защото там всички линии имат различни размери и изискват различни увеличения.
Има прост изход от това. Знаем, че истинският фрактал има безкрайно количество детайли. Това означава, че при увеличението му се появяват допълнителни детайли, които се прибавят към размера. В нефракталните фигури размерът никога не се изменя. Например, нека да разгледаме схемата по-долу, където има графика на размерите на някои нефрактали под различно увеличение. Ако направите графика на логаритъма на размера върху логаритъма на увеличението, ще се получат хоризонтални прави. Това показва, че размерите не се изменят, което значи, че фигурите не са фрактали.

Ако изследваме някои фрактали по същия начин, няма да получим хоризонтални прави, тъй като с увеличението, дължините растат. Това доказва,че фигурите са фрактали.
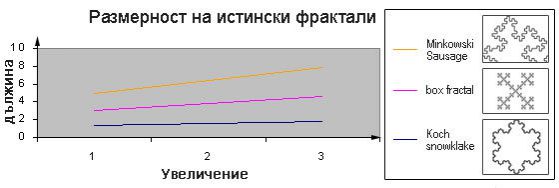
Сега можем лесно да изчислим фракталните размерности използвайки наклоните на правите. С простата формула:
фрактална размерност = наклон + 1
Геометричният метод може много ефективно да се използва за природни начупени форми с Брауново самоподобие. Използва се и за да се изчислят размерностите на крайбрежията, границите и облаците.
Метод броене на клетки

Методът на подобие и геометричният метод за изчисляване на фракталната размерност изискват измерване на размерите. За много фрактали това не само е сложно, но и почти невъзможно. Обърнете например, внимание на фрактала вдясно.
Вместо това, можем да използваме по-прост метод. Да поместим фрактала на лист карирана хартия, като страната на всеки квадрат има размер h. Нека преброим клетките, които не са празни. Броя им означаваме с променливата N. Намаляването на размера на квадратчетата прави сметката по-точна, което е равносилно на увеличение. Фактически увеличението e равно на 1/h. В раздела за метода на подобието за изчисляване на фракталната размерност употребихме формулата D= log N / log e. Сега можем да я заменим с: D = log N / log (1/h) Намалявайки h ще определим размерността все по-точно. За 3-мерни фрактали ще се използват кубове вместо квадрати, а за едномерните - отсечки.
Например, да изчислим фракталната размерност на фрактала Box (кутия). Поставяме го на карирана хартия - с размери на квадратите 1/3 и 1/9.
В първия случай 5 клетки не са празни. Във втория - 25. В първия случай:
D = log 5 / log (1/ (1/3)) = 1.46.
Във втория случай отговорът е същия, което означава, че изчислената размерност е точна.
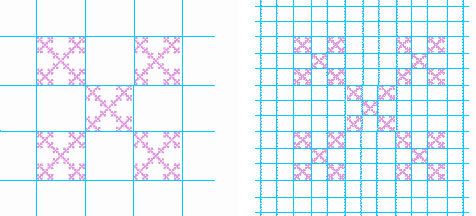

Този метод е много ефективен за природни форми, които е сложно да се измерят, особено култури бактерии.
Основни понятия и лексика
- Фрактали
- прах на Кантор
- Box (кутия)
- крива на Пеано
- Гръцки кръст
- крива на Кох
- Размерност
- топологична размерност
- дробна (фрактална) размерност
- Люис Фрай Ричардсън, бреговата линия на Англия
- Беноа Манделброт
- Логаритъм
- Методи за определяне на размерността
- Метод на подобието
- Геометричен метод
- Метод броене на клетки
Източници:
Фрактальная геометрия природы, Мандельброт Б.
Размерность пространства и фракталы, доклад прочитан 3 февраля 2007г. на семинаре “Мерность и фракталы”, Виталий Бойко
Фрактальная вселенная (Субъективный взгляд со стороны), Цицин Ф.А.,
Размер и размерность, Викиучебник
Фрактальные размерности, Евгений Епифанов
Анализ временных рядов: Фрактальные размерности
Въведение във фракталния анализ на природни структури. Цв. Георгиев




























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена