
Най-сетне, след осемгодишна сага на проверка на доказателство на хипотеза, която ще разтърси теорията на числата, докладът вече е готова да бъде официално публикуван.
През 2012 г. математикът Шиничи Мочизуки (Shinichi Mochizuki) от Университета в Киото в Япония представи доказателството на една от най-сложните и важни математически хипотези, хипотезата ABC.
Доказателството на Мочизуки, написано върху 500 страници в четири документа, е на толкова сложен стил, че теоретиците, които са способни да разберат основните му идеи, се броят на пръсти по света.
Работата му най-накрая е приета в рецензираното списание Publications of the Research Institute for Mathematical Sciences, но датата на публикуване все още не е определена.
Самият Мочизуки е главен редактор на списанието, което пък се издава от Университета в Киото. Той не е участвал в решението да се публикува доказателството, според Nature.
Мочизуки публикува доказателството на една от най-сложните и важни математически хипотези в своя блог и започва тихо да чака
Сутринта на 30 август 2012 г. японският математик Шиничи Мочизуки (Shinichi Mochizuki) публикува в своя уебсайт четири статии (1, 2, 3 и 4) с общо 512 страници - доказателство на abc-хипотезата, която се счита за едно от ключовите твърдения в теорията на числата, направи тогава кратко изложение Nature News.
Това е кулминацията на повече от едно десетилетие самотна работа. А Мочизуки просто я публикува в собствения си сайт и толкова. Не изпраща работата си в Annals of Mathematics. Не съобщава за нея в някой форум за математици.
Два дни по-късно услугата Google Scholar показва статиите на Мочизуки на Джордан Еленберг (Jordan Ellenberg), професор по математика в университета на Уисконсин-Медисън.
 Изображението е от анимация, създадена от Etienne Farcot на базата на спецификации, съставени от Шиничи Мочизуки и на предложения от Иван Фесенко, инициатор на среща на Института Клей по повод работата на японсклия математик.
Изображението е от анимация, създадена от Etienne Farcot на базата на спецификации, съставени от Шиничи Мочизуки и на предложения от Иван Фесенко, инициатор на среща на Института Клей по повод работата на японсклия математик.
Кой е Шиничи Мочизуки
Доказателството на abc-хипотезата се смята за толкова невъзможно, че малцина са математиците, които се осмеляват да се заемат с него. Повечето хора, които претендират за доказването на abc-хипотезата са отхвърлени като луди.
Но Мочизуки е различен от тези хора с непремерено самочувствие за възможностите си. Той прави кариера на математически гений - само за 2 години завършва едно от най-престижните висши училища в САЩ Philip Exeter Academy. Постъпва в Принстънския университет на 16 години и става доктор на математическите науки на 22. Става професор по 33, изключително ранна възраст за академичните среди.
Шиничи Мочизуки сега е номер едно теоретик в Университета Киото.
Мочизуки си изгради име за своите 20 години работа с редица значителни приноси към един сравнително нов, сложен клон на алгебричната геометрия, известен като неабелева геометрия. През 1998 г. той получи една от най-високите почести в математиката-покана за доклад на Международния конгрес на математиците, който се провежда на 4 години. След речта си през август 1998 г. в Берлин, той като че ли изчезва вдън земята в продължение на 14 години, за да работи по abc-хипотезата.

Неговата работа трябва да се вземе насериозно.
И в рамките на дни медиите поемат сензацията. Математическата общност имаше много причини за ентусиазъм. Всички са развълнувани, не защото някой е показал доказателство за важна хипотеза, а защото то се представя не от кой да е.
27 години, откакто е формулиран проблема, никой друг математик не е бил толкова близо до решаването му. Ако доказателство му се окаже вярно, това ще бъде едно от най-изумителните постижения на математиката този век и ще направи революция в проучването на уравнения с цели числа.
Почти няма кой да провери работата на Мочизуки
Материалът на Мочизуки е огромен - повече от 500 страници, целите гъсто запълнени със символи, прекалено абстрактен и неразбираем дори по стандартите на чистата математика. Не е лесно да се прочете доказателството, камо ли да се провери.
С тази нелека задача са се заели 10 математика.
За да се разбере защо случаят с Мочизуки е необичаен, трябва да го сравним с двете най-големи открития в математиката през последните 20 години: доказването на последната теорема на Ферма от британския математик сър Андрю Уайлс (той е посветен в рицарство за постижението си) през 1995 г. и доказателството за хипотезата на Поанкаре през 2003 г. от руския математик Григорий Перелман. Те са определени като изклюителни открития, тези доказателства превърнаха авторите си в двамата най-известни математици в света (заедно, може би, с Джон Наш от "Красив ум"). Но тяхната работа бе построена на базата на добре проучена математика, следвайки пътища, вече определени от други математици като възможни начини, които могат да доведат до доказателствата. В резултат на това на математическата общност бе в състояние да провери доказателствата на Уайлс и Перелман в сравнително кратко време.
Не е така положението с доказателството на Мочизуки.
 Преди математиците да започнат дори да четат доказателството или да разберат четирите негови статии, те трябва да проучат още 750 страници на невероятно сложната основополагаща работа на Мочизуки в областта на неабелевата геометрия. В момента има само около 50 души по света, които знаят неабелевата геометрия достатъчно добре, за да разберат тази предварителна работа. След това самото доказателство е написано в един напълно различен клон на математиката, наречен "интеруниверсална геометрия" (inter-universal geometry), в която Мочизуки, поне до този момент, той е сам, подчертава в статия Boston Globe.
Преди математиците да започнат дори да четат доказателството или да разберат четирите негови статии, те трябва да проучат още 750 страници на невероятно сложната основополагаща работа на Мочизуки в областта на неабелевата геометрия. В момента има само около 50 души по света, които знаят неабелевата геометрия достатъчно добре, за да разберат тази предварителна работа. След това самото доказателство е написано в един напълно различен клон на математиката, наречен "интеруниверсална геометрия" (inter-universal geometry), в която Мочизуки, поне до този момент, той е сам, подчертава в статия Boston Globe.
Веселин Димитров, студент в университета в Йейл, се запознава с предварителната работа на Мочизуки като подготовка за доказателството на японеца. Димитров пише: "Аз съм много впечатлен от единството и структурната съгласуваност в него".
Димитров подчертава, че е твърде рано да се прогнозира дали доказателството на Мочизуки ще издържи на строгата проверка. През октомври 2012 г. той и Акшай Венкатеш от Станфордския университет, изпращат писмо до Мочизуки, че са открили грешка в третата и четвъртата части на доказателството. Мочизуки признава грешката, но обяснява, че тя е незначителна и не влияе на основните изводи.
През декември 2013 г публикува коригираната версия на своето доказателство до януари. Мочизуки отказва всякакви интервюта и не напуска Киото.
Един от учените отбеляза, че японцът с поведението "показа среден пръст на математическата общност". Мочизуки се съгласява да отговаря на въпросите на своите колеги само по Skype. През декември 2015 в Оксфорд се проведе семинар по проблема с доказателството на abc-хипотезата, организиран от Математическия институт Клей. Мочизуки си остана у дома.
През 2018 г. математиците Петер Шолце (Peter Scholze) от Университета в Бон и Якоб Стикс (Jakob Stix) от Университета "Гьоте" в Германия заявиха, че са открили „сериозна, непоправима пропаст” в доказателството на Мочизуки. Те твърдяха, че някои от разсъжденията на Мочизуки са погрешни и че хипотезата ABC все още е открит проблем.
„Становището определено се измести към мнението, че доказателствата са погрешни след писмата на Шолце и Стикс през 2018 г.“, разказва Андрю Букър (Andrew Booker) от Университета в Бристол, Великобритания. „Очевидно е лошо за [теорията на числата], ако резултатът бъде обявен за теорема в някои кръгове, но не и в други.“
На пресконференция в петък в Киото, която обяви приемането на статията, на която Мочизуки не се яви, математикът Акио Тамагава (Akio Tamagawa) заяви, че доказателството не включва фундаментални промени в отговор на критиките на Стикс и Шолце.
В какво се състои abc-хипотезата или хипотезата на Естерле-Масер
Доказателството на abc-хипотезата, представено от Мочизуки през 2012 г., заема повече от 500 страници текст, а да го разберат и проверят могат малцина математици.
Аbc-хипотезата е предложена от математиците Дейвид Масер през 1985 г. и Джоузеф Естерле през 1988 г, независимо един от друг. Накратко тя изследва връзките между простите числа.
Хипотезата твърди, че за всяко реално число r>1 съществува краен брой тройки натурални числа a, b и c, за които се изпълняват условията:
- a + b = c;
- a, b и c са взаимно прости в съвкупност (т. е. нямат общи делители);
- c>rad (abc) r.
За да се разбере хипотезата на Естреле-Масер, са необходими малко обяснения и е нужно да се въведе понятието радикал. Радикал на числото rad(N) се нарича произведението на всички прости множители на това число. Например rad(24) =2*3 = 6 (защото 24 = 23*3). Това число има интересни свойства. Например, ако a и b са взаимно прости, т.е. нямат общи делители, различни от единица, то rad(ab) = rad(a) rad(b). Освен това, равенството rad(a) = a се изпълнява тогава и само тогава, когато a е произведение на различни прости числа. Например rad(15) = 15, защото това число има прости делители 3 и 5.
Да разгледаме сега тройката числа (a, b, c), за които a + b = c и тези три числа са взаимно прости. Естреле и Масер се интересуват от радикала на произведението на такива три числа, т. е. rad(abc), който е равен на rad(a), rad(b) или rad(c).
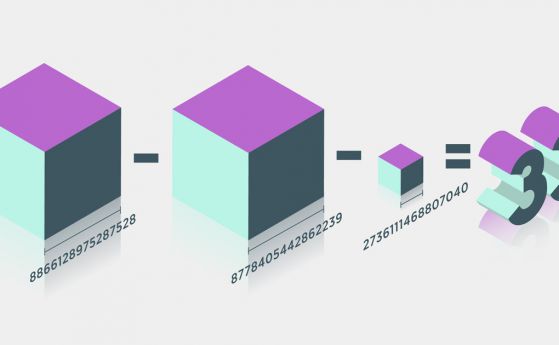
Например, да вземем тройката (2, 3, 5). За нея 5 < rad(2*3*5) = 2*3*5 = 30. Но за тройката (1, 8, 9) условието се изпълнява, 9 > rad(8*9) = rad(23*3 2) = 2*3 = 6.
Изследванията показват, че в някакъв смисъл тройките от първия тип са повече. Ако се вземе произволна тройка, която удовлетворява условието за взаимна простота и a + b = c, то почти винаги ще се изпълнява първото неравенство. Затова тройките, за които c > rad(abc), се наричат изключителни. Числен експеримент показва, че сред всички допустими тройки, при които с <50000, изключителни са само 276. Следователно, следващият естествен въпрос е: краен ли е броят на изключителните тройки? Оказва се, че са безкрайно много. Освен това е възможно да се намери такава серия от тройки, че съотношението rad(abc)/c да е произволно малко. Това означава липса на каквато и да е линейна оценка за стойността на радикала.
След като няма линейна оценка, то тогава може би съществува експоненциална. Тук на математиците им провървява и така се появява abc-хипотезата. Така се появява формулировката, която е в началото:
За всяко реално число r>1 съществува краен брой тройки натурални числа a, b и c, за които се изпълняват трите условия: a + b = c; a, b и c са взаимно прости; c>rad (abc)r.
Защо е толкова важна abc-хипотезата?
Работата е там, че за времето, откакто се появи тази хипотеза, математиците сведоха до нея много нерешени задачи. Те включват, например, хипотезата на Шпиро и хипотезата на Войта. Освен това бе установено, че от тази хипотеза може да се изведат редица фундаментални резултати не само в теорията на числата, но и в алгебричната геометрия - доказаната през 1983 г., хипотеза на Мордел и прословутата последна теорема на Ферма.
Източници:
Baffling 500-page ABC maths proof to be published after eight-year row, Newscientist
Monumental proof to torment mathematicians for years to come, Nature






















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews