
Седмици след като преодоляват една изключително трудна задача, свързана с числото 42 ("Отговорът на Живота, Вселената и Всичко останало"), математиците намериха решение за още по-труден проблем с числото 3.
В задачата се пита дали всяко цяло число може да бъде представено като сбор от три числа, повдигнати на трета степен.
Отдавна има две решения за числото 3, като и двете включват малки числа: 13 + 13 + 13 и 43 + 43 + (-5)3.
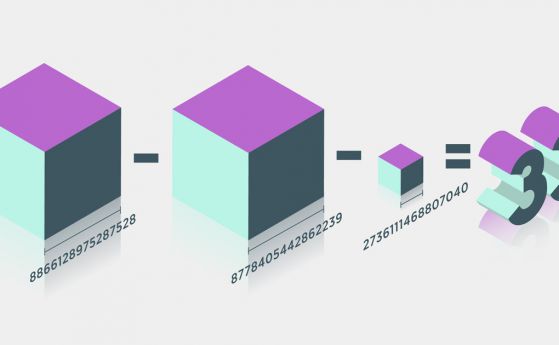
Но математиците търсят една трета възможност от десетилетия. Решението, което намериха Андрю Букър (Andrew Booker) от Университета в Бристол, Великобритания, и Андрю Съдърланд (Andrew Sutherland) от Масачузетския технологичен институт е:
5699368212219623807203 + (-569936821113563493509)3 + (-472715493453327032)3 = 3
По-рано този месец двамата математици намериха решение на задачата за числото 42, което бе последното останало нерешено число по-малко от 100.
За да намерят решението, Букър и Съдърланд използват от помощта на Charity Engine - инициатива, която обхваща целия свят, използвайки излишната изчислителна мощност на стотици хиляди домашни компютъра, които действат като своеобразен „планетарен суперкомпютър“. Времето за обработка е еквивалентно на един компютърен процесор, работещ непрекъснато в продължение на 4 милиона часа или повече от 456 години.
След като едно число може да бъде изразено като сбор от три куба, това означава, че има безкрайно много възможни решения, смята Букър. „Така че трябва да има безкрайно много решения за 3, а току-що намерихме третото“, отбелязва математикът.
Със сигурност се знае, че определени числа, като 4, 5 и 13, не могат да бъдат изразени като сума от три куба, както няма решение и за всяко k, което дава остатък 4 или 5, когато се раздели на 9. Това се дължи на факта, че кубовете на числата, когато се разделят на 9, могат да дадат остатък само 0, 1 и 8.
Има причина третото решение за 3 да е толкова трудно да се намери.
„Ако разглеждате решенията отделно за всяко просто число, те изглеждат случайни“, коментира Букър. Но ако вземем множеството начислата и решенията, което не е възможно, просто защото числата стават бързо много огромни - но ако съществува тази възможност, в тях ще видим някаква обща тенденция: големината на числата расте приблизително линейно с броя на решенията, които намерим, обяснява Букър.
Оказва се, че този темп на растеж е изключително малък за числото 3 - само 114, сега най-малкото нерешено число, има по-малък темп на растеж. С други думи, числата с бавен темп на растеж имат по-малко решения с по-малък брой цифри.
Двамата математици намериха решение и за задачата за числото 906. Така остават девет нерешени числа под 1000. Математиците смятат, че и те може да бъдат записани като сбор от три куба, но все още не знаем как.
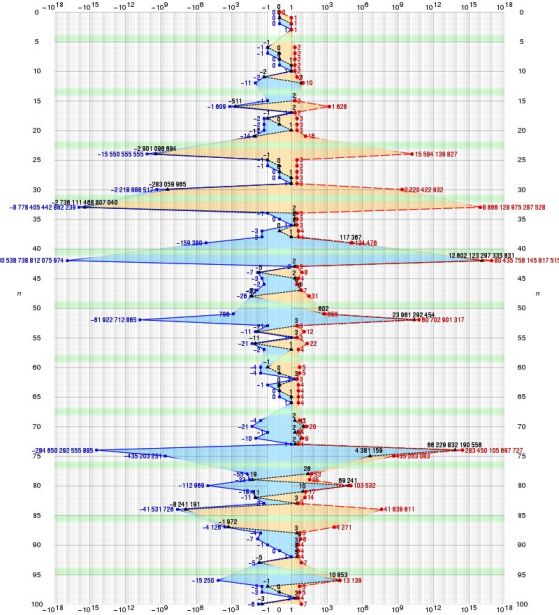 Полулогаритмична графика на решенията на x³ + y³ + z³ = k за целите числа x, y и z и n в интервала [0, 100]. Зелените ивици означават доказано отсъствие на решение. Кредит: Wikimedia Commons
Полулогаритмична графика на решенията на x³ + y³ + z³ = k за целите числа x, y и z и n в интервала [0, 100]. Зелените ивици означават доказано отсъствие на решение. Кредит: Wikimedia Commons
Уравненията в цели числа или диофантовите уравнения са специален начин за изследване на целите числа и техните свойства.
Според Букър проблемът „сума на три куба“ е „един от най-простите“ за диофантовите уравнения. „Точно на границата на това, с което можем да се справим”, добавя Браунинг.
Може би най-известният пример за такива уравнения е великата теорема на Ферма: x n + y n = z n за n> 2. Освен развитието на теорията на числата, търсенето на решения на диофантовите уравнения води до разработването на нови методи в математиката, които след това намират приложение в ежедневието.
Източник: Mathematicians find a completely new way to write the number 3, NewScientist





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews