
Терънс Тао е суперзвездата на математиката, носител на много награди, на 31-годишна възраст печели медала Фийлдс, наричан "математическият Нобел".
Сега той се доближи много до решението на един от най-известните нерешени проблеми в математиката, изключително трудна математическа задача, поставена за първи път преди 82 години.
Проблемът, известен като хипотезата на Колац (Collatz conjecture), наричан още "хипотеза 3n + 1", "сиракузки проблем". Хипотезата носи името на германския математик Лотар Колац, който формулира този проблем през 1 юли 1932 г.
Тя има проста формулировка, заради което е много популярна и доста аматьори се изкушават да се пробват, но винаги неуспешно. Доказателството на Тао е 48 страници сложна авангардна математика, надграждаща работата на други изследователи. Въпреки това той не твърди, че има пълното доказателство, а само частични резултати.
За да обясним същността й, ще разгледаме следната последователност от числа, наречена сиракузка последователност. Вземете кое да е естествено (положително цяло) число n. Ако е четно, тогава го разделете на 2, а ако е нечетно, го умножете по 3 и добавете 1 (получаваме 3n + 1). Извършваме същите действия върху полученото число и т.н.
Хипотезата на Колац гласи, че независимо кое число n вземем първоначално, рано или късно ще получим 1. Например 10, 5,16, 8, 4, 2, 1.
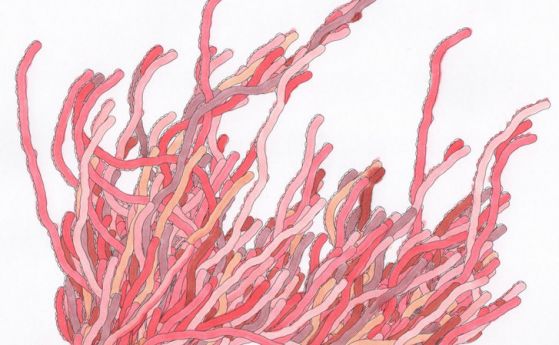
Ако се изобрази последователността на Колац от 1 наобратно към различни изходни точки, получаваме характерен модел на храст, наподобяващ също водорасли или купчина странни червеи.
 Кредит: Edmund Harriss
Кредит: Edmund Harriss
Визуалното представяне е лесно, но е трудно да се докаже дали хипотезата е вярна или невярна.
Към април 2019 г. всички естествени числа, по-малки от 1 152 921 504 606 846 976, са проверени и всякo от тях за краен брой стъпки съответства на условията на хипотезата на Колац. Но доказването не включва просто проверка на все повече числа - числовата линия е безкрайна - а намирането на логически обосновано математическо обяснение.
Докато не докажем математическо твърдение, не можем да го наречем теорема, а само предположение. Понякога най-простите твърдения са най-трудни за доказване, въпреки че са верни за милиони и дори трилиони числачи не са намерили такива, за които не са верни.
 График на последователността за число 27: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 . Кредит: Wikimedia Commons
График на последователността за число 27: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 . Кредит: Wikimedia Commons
Сега математикът Терънс Тао (Terence Tao) от Университета на Калифония, Лос Анджелис, изглежда "почти" е успял да докаже хипотезата на Колац.
Терънс Тао обяви, че има нови частични резултати в доказването на хипотезата на Колац. Неговите публикация в блога и arXiv са озаглавени „Почти всички орбити на Колац постигат почти ограничени стойности" (Almost all orbits of the Collatz map attain almost bounded values).
Какво означава това? Орбитите на Колац са просто поредиците, които се получават по време на процеса, който демонстрирахме. Орбитата на Колац за 10 е (10, 5, 16, 8, 4, 2, 1, 4, 2, 1,…). Тъй като половината от 4 е 2, половината от 2 е 1, а 3 * 1 + 1 е 4, Орбитите на Колац винаги преминават през 4, 2 и 1.
Защо това е важно? Причината е, че ако може да се докаже, че минимумът на последователността на Колац за N винаги е по-малък от N за всички N> 1, тогава хипотезата на Колац е доказана. Причината е проста. Ако получите стойност m, която е по-малка от N, тогава останалата част от последователността за N е същата, както ако сте започнали от m и затова сега имаме, че минимумът за последователността е по-малък от m. Можем да повтаряме процеса назад, за да докажем, че минимумът трябва да е 1.
Дао не доказва точно това, но доказа теоремата:
Нека f е коя да е функция, дефинирана за цели числа, с изключение на нула, и f (N) клони към безкрайност с N, тогава минимумът на последователността на Колац за N е по-малък от f (N) за почти всички N. В такъв случай минималната стойност на Колац за N е по-малка от N.
Значи ли това, че проблемът е решен?
Не точно.
Важна подробност в заглавието на работата на Тао е думата "почти". Тази дума е последната бариера пред цялостното решение и има различно значение в различни математически контексти.
Техническият термин в случая е логаритмична плътност, която се изучаеи в вероятностната теория на числата (англ. Probabilistic number theory).
Какво е аритметична плътност? Интуитивно усещаме, че сред естествените числа има повече „нечетни“ числа от квадрати на цели числа. Но множеството на нечетните числа всъщност не е „по-голямо“ от множеството на квадратите - и двете множества са безкрайни и изброими и по този начин могат да се приведат в съответствие „едно към едно“. Очевидно, за да формализираме интуитивната си концепция, се нуждаем от по-добър начин. Представата за аритметична плътност прави тази интуиция прецизна.
Аритметичната плътност описва колко редки са контрапримерите на Колац, ако изобщо съществуват. Те биха могли да съществуват, но тяхната честота клони към 0, слизайки надолу по числовата линия. Целта остава да се докаже, че те изобщо не съществуват.
По същество резултатите на Тао доказват, че всякакви контрапримери за преположението на Колац ще са невероятно редки.
Тогава на крачка ли сме от цялостно решение? Е, дори Тао казва "не".
Както Тао пише в отговор на коментар към публикацията си в блога:
"... това е една от тези ситуации, при които изглежда има огромна разлика в трудността между "почти всички резултати" и "всички резултати".
Тао обяснява, че има много малък шанс методът, който използва, някога да даде окончателни доказателства и всъщност не иска да се занимава с проблема повече.
Изглежда, че математиците ще могат да използват последните иновации на Тао, за да решат (или почти да решат) други големи проблеми, но вероятно хипотезата на Колац ще си остане "хипотеза" за десетилетия и ще са нужни напълно нови клонове на математиката, за да бъде решена.
Ако имате интерес, има онлайн калкулатор на Колац, в който можете да генерирате серия от собствени начални стойности.
Справка: arxiv.org/909.03562
Източници:
Terry Tao Almost Proves Collatz Conjecture, i-programmer.info
Baffling maths riddle that looks like a pile of worms almost solved, newscientist
Mathematicians Are So Close to Cracking This 82-Year-Old Riddle, popularmechanics
A matematika Mozartja majdnem bizonyította a 82 éve megoldatlan Collatz-sejtést, Molnár Csabakövetés






















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews