Андрю Букър, математик от Университета в Бристол, намери ново решение на диофантовото уравнение x 3 + y 3 + z 3 = k, в което k = 33, едно уравнение, останало нерешено 64 години, съобщава Quanta Magazine.
Хипотезата, че всяко естествено число, което разделено на девет не дава остатък 4 или 5, може да бъде представено като сума от кубовете от три цели числа е формулирана преди няколко десетилетия. От 1954 г. досега учените са успели да намерят тройки кубове за всички такива числа по-малки от сто, с изключение на две: 33 и 42.
33 бе особено труден случай, докато Букър не намери своето решение, сега единственият останал е за k=42.
А решението на Андрю Букър (Andrew Booker) е:
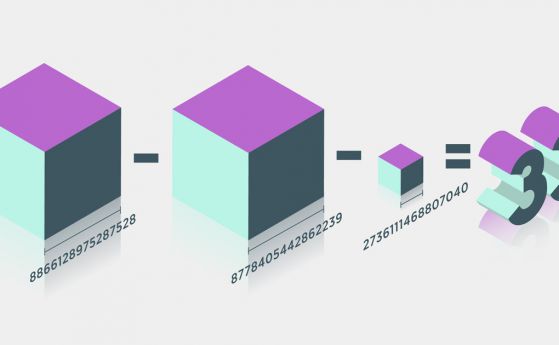
(8,866,128,975,287,528)³ + (–8,778,405,442,862,239)³ + (–2,736,111,468,807,040)³ = 33.
Препринтът на статията е публикуван в axiv.org.
Букър откри тази странна тройка от 16-цифрени числа, като измисли нов алгоритъм за търсене, за да ги отсее от квадрилион възможности. Алгоритъмът бе пуснат в университетския суперкомпютър в продължение на три седмици. (Математикът разказва, че е смятал, че ще са нужни шест месеца, но решението „изскочи, преди да го очаквам.“) Когато новината за неговото решение се появи в интернет по-рано този месец, колегите му теоретици и любители на математиката бяха трескави от вълнение. Според видеофилма горе за това откритие, самият Букър буквално скачал от радост в кабинета си, когато разбрал.
Причината, поради която толкова дълго време не се намери решение за 33, е, че търсенето отива доста далеч по цифровата линия - чак до 10 16 , или десет квадрилиона, и точно толкова далеч назад в отрицателните числа и да бъде намерена числовата тройка е непосилна задача, докато Букър не измисля своя алгоритъм. "Той не просто е пуснал да се търси това на по-голям компютър в сравнение с компютрите преди 10 години - той намери истински по-ефективен начин за намиране на решенията", коментира Тим Браунинг (Tim Browning), математик, специалист по теория на числата в Института за наука и технологии в Австрия.
Предишните алгоритми „не знаеха какво търсят“, обясни Букър, те биха могли ефективно да търсят в даден диапазон от цели числа за решения на k = x ³ + y ³ + z ³ за всяко цяло число k , но те не могат да се насочат към конкретно k, като k = 33. по този начин неговият алгоритъм работи "може би 20 пъти по-бързо на практика", отбелязва Букър, отколкото алгоритмите с нецелеви подход.
Уравненията в цели числа или диофантови уравнения са специален начин за изследване на целите числа и техните свойства.
Според Букър проблемът „сума на три куба“ е „един от най-простите“ за диофантовите уравнения. „Точно на границата на това, с което можем да се справим”, добавя Браунинг.
Може би най-известният пример за такива уравнения е великата теорема на Ферма: x n + y n = z n за n> 2. Освен развитието на теорията на числата, търсенето на решения на диофантовите уравнения води до разработването на нови методи в математиката, които след това намират приложение в ежедневието.
Ние се сблъскваме с най-простите примери на диофантови уравнения, когато се опитваме да платим за покупка без ресто - например, ако имате банкноти от 2 и 5 лева, може да съберете 19 лева само по два начина - да вземете две банкноти или монети от два лева и три банкноти от пет лева или седем банкноти/ монети от два лева и една от пет лева. В този случай всъщност решаваме диофантовото уравнение 19 = 2x + 5y в естествени числа.
Представянето на естествените числа като сума от кубове на цели числа е много по-сложен и интересен проблем от областта на диофантовите уравнения. Изглежда много необичайно, че за много числа, например k = 29, решенията на уравнението изглеждат лесно: x 3 + y 3 + z 3 = 29 има решение за x = 3, y = z = 1. Но вече за k = 30 решението се достига само при x = 3 982 933 876 681, y = -636 600 549 515 и z = -3 977 505 554 546, а за k = 31 и 32 няма никакво решение, както и за всяко k, което дава остатък 4 или 5, когато се раздели на 9. Това се дължи на факта, че кубовете на числата, когато се разделят на 9, могат да дадат остатък само 0, 1 и 8. За уравнението x 3 + y 3 + z 3 = 33 не са били известни стойности за x, y и z под 100 трилиона.
Андрю Букър е вдъхновен от видеото (горе) на блогъра Numberphile и решава да се опита да реши задачата с числото 33. За тази цел, математикът разработва алгоритъм, който позволява да се подбират стойностите на променливите много ефективно. Идеята е, че ако преместите един от кубовете в лявата част на уравнението, тогава и двете части трябва да се делят на (x + y):
x 3 + y 3 + z 3 = 33
x 3 + y 3 = 33 - z 3
(x + y) (x 2 - xy + y 2 ) = 33 - z 3
По този начин е възможно да се подбират само определени делители за всяко z. В резултат на това след около месец обработка на суперкомпютъра Андрю Букър успява да намери решение за k = 33.
33 = 8 866 128 975 287 5283 + (−8 778 405 442 862 239)3 + (−2 736 111 468 807 040)3
Интересно е, че за k = 42 решения с x, y, z по-малки от 10 трилиона не могат да бъдат намерени. Сред останалите k <1000, за които все още не е намерено решение, остават само числата 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, 975. Освен x = y = z = 1 не съществуват други решения за k = 3. Въпреки това съществува хипотеза, че за всяко подходящо k има безкрайно множество от тройки x, y, z.
Още по темата
Физика
Карен Уленбек е първата жена, спечелила престижната награда по математика Абел
Математика
Скромният гений Григорий Перелман - математикът, решил задачата на хилядолетието
Математика
Българинът, който се зае да провери доказателството на abc-хипотезата
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари