
Математиците най-накрая успяха да решат една задача, върху която е мислено 65 години. Те намериха сумата на кои три числа, повдигнати на трета степен, е 42.
Задачата е поставена през 1954 г. и най-общо е за представянето на цяло число във вид на сума от три куба на цели - положителни или отрицателни - числа, и звучи така:
x 3 + y 3 + z 3 = k. Където k може да е всяко от числата от 1 до 100. Въпросът е, кои са x, y и z?
Представянето на естествените числа като сума от кубове на цели числа е сложен и интересен проблем. Изглежда много необичайно, че за много числа, например k = 29, решенията на уравнението изглеждат лесно: x 3 + y 3 + z 3 = 29 има решение за x = 3, y = z = 1. Но вече за k = 30 решението се достига само при x = 3 982 933 876 681, y = -636 600 549 515 и z = -3 977 505 554 546, а за k = 31 и 32 няма никакво решение, както и за всяко k, което дава остатък 4 или 5, когато се раздели на 9. Това се дължи на факта, че кубовете на числата, когато се разделят на 9, могат да дадат остатък само 0, 1 и 8.
През следващите десетилетия са намерени по-лесните решения. През 2000 г. математикът Ноам Елкис (Noam Elkies) от Харвардския университет публикува алгоритъм, който да помогне да се намерят по-трудните.
През 2015 г. Тим Браунинг записва видео в YouTube за задачата с 33 по популярния математически канал Numberphile, в което обяснява проблема. По това време единствените числа, по-малки от 100, за които не е решена задачата, са 33, 42 и 74. Това видео достигна до по-широка аудитория, което доведе до поредица от пробиви.
Вдъхновен от видеоклипа на Numberphile, в рамките на няколко месеца Сандър Хайсман (Sander Huisman) от Амстердамския университет намира решение за 74:
74=(−284650292555885)3+662298321905563+2834501056977273
Numberphile записва още едно видео за решението на Хайсман, отново с Тим Браунинг. Друг математик, Андрю Букър (Andrew Booker) от Университета в Бристол, Великобритания, преглежда видеото и написва нов алгоритъм, който позволява да се подбират стойностите на променливите много ефективно. Идеята е, че ако преместите един от кубовете в лявата част на уравнението, тогава и двете части трябва да се делят на (x + y):
x 3 + y 3 + z 3 = 33
x 3 + y 3 = 33 - z 3
(x + y) (x 2 - xy + y 2 ) = 33 - z 3
По този начин е възможно да се подбират само определени делители за всяко z. В резултат на това само след три седмици обработка с мощния суперкомпютър в Университетския център за модерни компютърни изследвания Андрю Букър успява да намери решение за k = 33:.
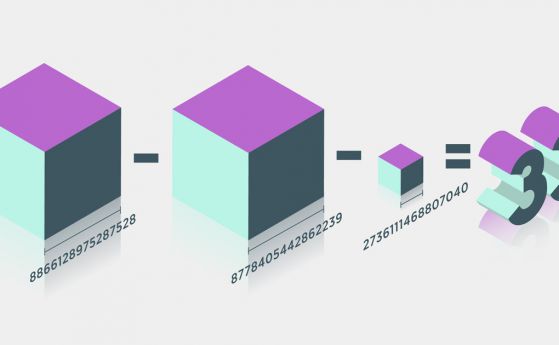
33 = 8 866 128 975 287 5283 + (−8 778 405 442 862 239)3 + (−2 736 111 468 807 040)3
И така, остана най-трудният случай от всички: 42.
Интересно е, че за k = 42 решения с x, y, z по-малки от 10 трилиона не могат да бъдат намерени.
Това се оказа много по-упорит проблем, затова Букър включва и колегата си, математикът от Масачузетския технологичен институт (MIT) Андрю Съдърланд (Andrew Sutherland), експерт в масово паралелно изчисляване.
И успяват. Освен това математиците обявиха резултата си забавно като тихомълком замениха началните страници на личните си сайтове с израза "Животът, Вселената и всичко останало", като реверанс към Дъглас Адамс, съобщaва The Aperiodical.
Математиците не стигат лесно до резултата. Те се възползват и от помощта на Charity Engine - инициатива, която обхваща целия свят, използвайки излишната изчислителна мощност на над 500 000 домашни компютъра, които действат като своеобразен „планетарен суперкомпютър“.
Бяха нужни над един милион часа изчислително време, но двамата математици намериха своето решение.
X = -80538738812075974
Y = 80435758145817515
Z = 12602123297335631
И така, пълното уравнение е (-80538738812075974) 3 + 80435758145817515 3 + 12602123297335631 3 = 42.
"Чувствам облекчение", заяви Букър.
"В тази игра е невъзможно да сте сигурни, че ще откриете нещо. Това е малко като опит за прогнозиране на земетресенията, тъй като имахме само груби вероятности. Така че можеше да намерим това, което търсим, след няколко месеца работа или да не стигнем до решението след век".
Това ли е всичко? Не, разбира се.
Намерени са числата само от 1 до 100. Ако се качим с порядък - до 1000, остават числата 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, 975, за които все още не е намерено решение,
Освен x = y = z = 1 не е намерено друго решение за k = 3.
Така че има още работа за математиците.
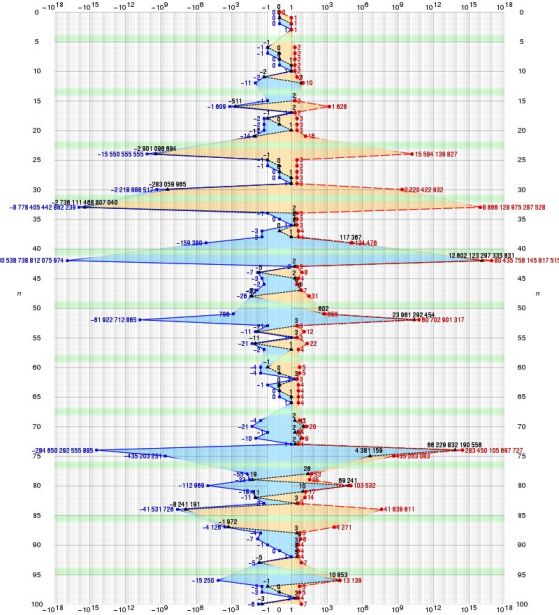 Полулогаритмична графика на решенията на x³ + y³ + z³ = k за целите числа x, y и z и n в интервала [0, 100]. Зелените ивици означават доказано отсъствие на решение. Кредит: Wikimedia Commons
Полулогаритмична графика на решенията на x³ + y³ + z³ = k за целите числа x, y и z и n в интервала [0, 100]. Зелените ивици означават доказано отсъствие на решение. Кредит: Wikimedia Commons
Уравненията в цели числа или диофантовите уравнения са специален начин за изследване на целите числа и техните свойства.
Според Букър проблемът „сума на три куба“ е „един от най-простите“ за диофантовите уравнения. „Точно на границата на това, с което можем да се справим”, добавя Браунинг.
Може би най-известният пример за такива уравнения е великата теорема на Ферма: x n + y n = z n за n> 2. Освен развитието на теорията на числата, търсенето на решения на диофантовите уравнения води до разработването на нови методи в математиката, които след това намират приложение в ежедневието.
Ние се сблъскваме с най-простите примери на диофантови уравнения, когато се опитваме да платим за покупка без ресто - например, ако имате банкноти от 2 и 5 лева, може да съберете 19 лева само по два начина - да вземете две банкноти или монети от два лева и три банкноти от пет лева или седем банкноти/ монети от два лева и една от пет лева. В този случай всъщност решаваме диофантовото уравнение 19 = 2x + 5y в естествени числа.
Източник:
Mathematicians Solve '42' Problem With Planetary Supercomputer, ScienceAlert
42 is the answer to the question “what is (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³?”, The Aperiodical






















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews