

–Ш–Ї–Њ–љ–Њ–Љ–Є—Б—В—К—В –Ф–Њ–±—А–Є –С–Њ–ґ–Є–ї–Њ–≤ –њ—Г–±–ї–Є–Ї—Г–≤–∞ –≤ –Є–љ—В–µ—А–љ–µ—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї–љ–Њ —А–µ—И–µ–љ–Є–µ –љ–∞ –Ј–∞–і–∞—З–∞, –љ–∞–і –Ї–Њ—П—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ¬†—А–∞–Ј–Љ–Є—И–ї—П–≤–∞—В –Њ—В 40 –≥–Њ–і–Є–љ–Є.
–°—В–∞–≤–∞ –≤—К–њ—А–Њ—Б –Ј–∞ "P versus NP problem". –Э–∞–є-–Њ–±—Й–Њ –Ї–∞–Ј–∞–љ–Њ –Ј–∞–і–∞—З–∞—В–∞ –Ј–∞–і–∞–≤–∞ –≤—К–њ—А–Њ—Б–∞: "–Р–Ї–Њ —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –≤—Б–µ–Ї–Є –њ—А–Њ–±–ї–µ–Љ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –±—К—А–Ј–Њ –њ—А–Њ–≤–µ—А–µ–љ–Њ –Њ—В –Ї–Њ–Љ–њ—О—В—К—А, –Љ–Њ–ґ–µ –ї–Є –Є –і–∞ –±—К–і–µ –±—К—А–Ј–Њ –љ–∞–Љ–µ—А–µ–љ–Њ –Њ—В –Ї–Њ–Љ–њ—О—В—К—А?". –Ш–ї–Є, —Б–њ–Њ—А–µ–і –і—Г–Љ–Є—В–µ –љ–∞ –С–Њ–ґ–Є–ї–Њ–≤, –Љ–Њ–ґ–µ –ї–Є —З—А–µ–Ј –њ—А–Њ—Б—В–Є –Ј–∞–і–∞—З–Є (P) –і–∞ —Б–µ —А–µ—И–∞–≤–∞—В —Б–ї–Њ–ґ–љ–Є –Ј–∞–і–∞—З–Є (NP). (P –Є NP —Б–∞ –Њ–Ј–љ–∞—З–µ–љ–Є—П –љ–∞ –њ–Њ-—Б–ї–Њ–ґ–љ–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –µ–ї–µ–Љ–µ–љ—В–Є, –љ–Њ —В—Г–Ї —Й–µ –≥–Є –љ–∞—А–Є—З–∞–Љ–µ "–Ј–∞–і–∞—З–Є", —Б—К–Њ—В–≤–µ—В–љ–Њ "–њ—А–Њ—Б—В–Є" –Є–ї–Є "—Б–ї–Њ–ґ–љ–Є" - –±.–∞.).
"–Р–Ї–Њ –Ї–Њ–Љ–њ—О—В—К—А—К—В –Ј–љ–∞–µ, —З–µ 3+2 –њ—А–∞–≤–Є 5, —В–Њ –Љ–Њ–ґ–µ –ї–Є, –∞–Ї–Њ –Љ—Г —Б–µ –Ј–∞–і–∞–і–µ –і–∞ –Ї–∞–ґ–µ –Ї–Њ–Є –і–≤–µ —З–Є—Б–ї–∞ –њ—А–∞–≤—П—В 5, —В–Њ–є –і–∞ –і–∞–і–µ –Њ—В–≥–Њ–≤–Њ—А "3+2" –±–µ–Ј –і–∞ –њ—А–Њ–≤–µ—А—П–≤–∞ –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є?", –њ–Є—В–∞ —Б–µ –µ –Є –∞–≤—В–Њ—А—К—В –љ–∞ –љ–Њ–≤–Њ—В–Њ —А–µ—И–µ–љ–Є–µ.
–°–њ–Њ—А–µ–і –Є–Ї–Њ–љ–Њ–Љ–Є—Б—В–∞, –∞–Ї–Њ —Б–µ –Њ–Ї–∞–ґ–µ, —З–µ –µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ —З—А–µ–Ј P –і–∞ —Б–µ —А–µ—И–Є NP, —В–Њ–≤–∞ —Й–µ —Б—К–Ї—А–∞—В–Є –Њ—Б–µ–Ј–∞–µ–Љ–Њ –≤—А–µ–Љ–µ—В–Њ –Ј–∞ –њ–Њ—Б—В–Є–≥–∞–љ–µ –љ–∞ –њ—А–Њ–≥—А–µ—Б –≤ –і–∞–і–µ–љ–∞ –Њ–±–ї–∞—Б—В (–љ–Њ–≤–Є –ї–µ–Ї–∞—А—Б—В–≤–∞, –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ–Њ—Б–ї–µ–і–Є—Ж–Є –Њ—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ —А–µ—И–µ–љ–Є–µ –≤ –Ї–Њ—Б–Љ–Њ—Б–∞ –Є –і—А., –Ї–Њ–Є—В–Њ –Є–Љ–∞—В –љ—Г–ґ–і–∞ –Њ—В –≥–Њ–ї–µ–Љ–Є –Є–Ј—З–Є—Б–ї–µ–љ–Є—П).
–†–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –С–Њ–ґ–Є–ї–Њ–≤ –Њ–±–∞—З–µ –≥–ї–∞—Б–Є, —З–µ —В–Њ–≤–∞ –µ –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Њ. –¶–µ–ї—В–∞ –љ–∞ –∞–≤—В–Њ—А–∞ –µ —А–µ—И–µ–љ–Є–µ—В–Њ –Љ—Г –і–∞ –±—К–і–µ —А–∞–Ј–≥–ї–µ–і–∞–љ–Њ –Є –њ—А–µ—Ж–µ–љ–µ–љ–Њ –і–∞–ї–Є –µ –≤—П—А–љ–Њ. –Р–Ї–Њ —Б–µ –Њ–Ї–∞–ґ–µ, —З–µ –µ –≤—П—А–љ–Њ, —В–Њ —В–Њ–є —Й–µ –њ–Њ–ї—Г—З–Є 1 –Љ–ї–љ. –і–Њ–ї–∞—А–∞, —В—К–є –Ї–∞—В–Њ –Њ–њ–Є—Б–∞–љ–Є—П—В –Ї–∞–Ј—Г—Б –µ –≤–Ї–ї—О—З–µ–љ –Ї—К–Љ –Ч–∞–і–∞—З–Є—В–µ –љ–∞ —Е–Є–ї—П–і–Њ–ї–µ—В–Є–µ—В–Њ. –Ш–Ї–Њ–љ–Њ–Љ–Є—Б—В—К—В —Б–µ –µ –Њ–њ–Є—В–∞–ї –і–∞ –њ—Г–±–ї–Є–Ї—Г–≤–∞ —Б–≤–Њ—П —В—А—Г–і –≤ –∞—А—Е–Є–≤–∞ –љ–∞ –±–Є–±–ї–Є–Њ—В–µ–Ї–∞—В–∞ –љ–∞ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ "–Ъ–Њ—А–љ–µ–ї", –љ–Њ –Љ–Њ–і–µ—А–∞—В–Њ—А–Є—В–µ —Б–∞ –≥–Њ –Њ—В—Е–≤—К—А–ї–Є–ї–Є.
"–Ш–Ј–њ—А–∞—В–Є—Е –≥–Њ –Є –љ–∞ –љ—П–Ї–Њ–ї–Ї–Њ –њ—А–Њ—Д–µ—Б–Њ—А–Є, –љ–Њ —В–µ —Б–µ —И–µ–≥—Г–≤–∞—В –Є –Ї–∞–Ј–≤–∞—В, —З–µ –љ–µ –µ —В–∞–Ї–∞. –°–∞–Љ–Њ —З–µ –љ–µ –Љ–Є –Ї–∞–Ј–≤–∞—В –Ј–∞—Й–Њ –љ–µ –µ —В–∞–Ї–∞. –Ґ–Њ–≤–∞ –µ, –Ї–Њ–µ—В–Њ –Љ–µ –≥–ї–Њ–ґ–і–Є - –∞–Ј –≤–Є–ґ–і–∞–Љ, —З–µ –љ–µ—Й–Њ –љ–µ –Љ–Є —Е–∞—А–µ—Б–≤–∞ –≤ —А–µ—И–µ–љ–Є–µ—В–Њ, –љ–Њ –љ–µ –Љ–Њ–≥–∞ –і–∞ –≤–Є–і—П –Ї—К–і–µ –±—К—А–Ї–∞–Љ", –Ї–∞–Ј–≤–∞ —Б–∞–Љ–Є—П—В –С–Њ–ґ–Є–ї–Њ–≤.
–Ґ—К–є –Ї–∞—В–Њ –і–∞ —Б–µ –Њ–±—П—Б–љ–Є —В–Њ–≤–∞ —А–µ—И–µ–љ–Є–µ –љ–µ –µ –њ–Њ —Б–Є–ї–Є—В–µ –љ–∞ –≤—Б–µ–Ї–Є, –≥–Њ –њ—Г–±–ї–Є–Ї—Г–≤–∞–Љ–µ —В—Г–Ї –≤ –њ—К–ї–љ–Є—П –Љ—Г –≤–Є–і –Є —Б–µ –љ–∞–і—П–≤–∞–Љ–µ –љ—П–Ї–Њ–є –і–∞ –і–∞–і–µ –Њ—В–≥–Њ–≤–Њ—А –љ–∞ –≤—К–њ—А–Њ—Б–∞ –њ—А–∞–≤ –ї–Є –µ –Ф–Њ–±—А–Є –С–Њ–ґ–Є–ї–Њ–≤, –Ї–∞—В–Њ –Ї–∞–Ј–≤–∞, —З–µ –љ–µ –µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ —З—А–µ–Ј –њ—А–Њ—Б—В–Є –Ј–∞–і–∞—З–Є –і–∞ —Б–µ —А–µ—И–∞–≤–∞—В —Б–ї–Њ–ґ–љ–Є.
PвЙ†NP, proven by an analysis of "Subset sum problem"
1.Solution in short
To have a вАЬwormholeвАЭ you need a worm to dig it. If no worm, no hole eitherвА¶
In short this is the solution of вАЬP vs. NPвАЭ problem. The answer is вАЬNoвАЭ. P is not equal to NP, as there is no вАЬwormвАЭ to dig a shortcut and this way bypass the exponential algorithm tragedy. There is no shortcut and such one is impossible. The purpose of this article is to prove this.
To achieve this the concept of this article is to prove that a specific NP-complete problem cannot be solved non-exponentially. This will prove that PвЙ†NP, because otherwise contradiction will appear. If a NP-complete problem is proved as un-solvable in polynomic time and another NP-complete is solved then the first will also be solved as it could be converted into second one. Obviously not-possible.
To prove this assertion we can use the вАЬSubset sum problemвАЭ. If we prove that it cannot be solved non-exponentially, this will be the end of вАЬP vs. NPвАЭ discussion.
And the answer of вАЬSubset sum problemвАЭ is very short and simple:
You can not avoid exponents (xn) in a problem where combinatorics is involved. No such possibility. And that is in short the solution of вАЬP vs. NPвАЭ. P is not equal to NP.
You donвАЩt need to read any more this article unless you are keen on brain gymnastics and developing intellect by thinking on complex issues. If you are interested just in the answer, that is all вАУ exponents are inevitable with combinatorics involved.
And you can not solve the subset sum problem without combinatorics. Theoretically if such a decision was possible, so it will mean existence of functional dependency between the numbers. Functional dependency and calculating by formula is the only way to find the right answer among many other wrong answers. But this will contradict the initial condition of the problem вАУ finding a subset in a set of arbitrary integers. The problem is defined as universal вАУ the algorithm must work on ANY set of integers. And this excludes functional dependency. As no dependency exists, combinatorics is the way. And combinatorics means exponents.
You can do whatever you want with the initial set (below are some thoughts on this), but never the less what you do, some subset will remain for combinatorial checkup. Therefore the only result of your effort will be a hypothetic reduction of the exponent size (xn, xn/2вА¶xn/1000вА¶). But in all these cases some exponential element will remain. Generally the most used approach in this area is splitting the initial set to subsets, because this way the exponential power goes down. But anyway there remains an exponential component. In addition, splitting has some limits. You can not split too much, because you will start missing some combinations containing possible solution. To avoid this you will have to combine again subsets each other and this will bring you back to a previous level of splitting. But this is in the next part of analysis. The real solution of вАЬP vs. NPвАЭ is as follows:
вАЬSubset sum problemвАЭ is a complete NP-problem. вАЬSubset sum problemвАЭ can not be solved without using combinatorics at all. The existence of combinatorics means unavoidable exponents. And this means that no pure polynomic solution is possible. As вАЬSubset sum problemвАЭ is proven unsolvable in polynomic time, and as it is a NP-complete, therefore:
PвЙ†NP
2.Some thoughts on what is theoretically lowest needed complexity for вАЬSubset sum problemвАЭ
Now letвАЩs return to the initial epigramвА¶
To have a вАЬwormholeвАЭ you need a worm to dig it. If no worm, no hole eitherвА¶
So letвАЩs start searching for вАЬwormsвАЭ. I.e. for something that could help us reduce this horrifying check-all-combinations calculation burden. What could help us avoid this? Is there a вАЬwormвАЭ, a вАЬprivilegeвАЭ, any concept that could help us?
Unfortunately No.
All we have is a set of numbers. And nothing more. No number is marked as preferable. No any arithmetic operation on numbers can help us avoid some of the calculations. There is nothing that can help us. No вАЬwormвАЭ to dig. No вАЬfiltering privilegeвАЭ to send in trash these unneeded and exhausting combinations. No such savior among numbers.
Anyway we have something that can help. But not enough. We have 3 important things that can be used for filtering:
-We have the initial set itself and can somehow manipulate it. Generally we can split it
-We have a target number that the subsets must equal - for simplification we could accept this as zero(0).
-We have the value of the current calculated combination
That is all we have. In fact these elements can be used for some filtering. But not enoung to make any potential algorithm non-exponential. In fact in one way or another exactly these 3 elements are used in all algorithms for solving the problem, including the most effective ones. These elements can be used in different ways вАУ directly or indirectly, by summing, sorting, merging, etc. But all ways descend visibly or not, from these 3 вАУ manipulating the set, target number and value of current calculated combination.
So if based only on these 3 factors (worms, privilege filters) we can not have a non-exponential solution, therefore we can not have such a solution at all.
So the purpose of the second part of this article is to find the filtering limit, based on the set, current calculated value and target number.
LetвАЩs start with the set, because this is used together with the rest 2 factors.
Splitting the set is a powerful tool of lowering the exponential power. Working with smaller subsets you can reduce the number of combinations to be checked. Using it along with other filters the overall job done will go down. Anyway splitting does not remove the exponential nightmare for the computer. It just makes it smaller.
In addition there are limits of splitting. If you split only in 2, then you will lower the exponent power to the level of the bigger subset. If 2 subsets are equal, you will have exponential power of n/2. So why not then spilt in 4,5вА¶1000? Why not split until we reach a subset of 1 number and solve the problem instantly? The answer is obvious. If you split on more than 2 subsets, you risk starting to miss some of the combinations needed for check. To avoid this you will have to combine again subsets each other. And this will bring you back to a previous level of splitting. At last you will be back to the initial split in 2 subsets. In this case with any subset having just one another subset as a possible вАЬpartnerвАЭ there is no risk of missing combinations. So the theoretical limit of filtering power of splitting is n/2.
Now letвАЩs go to the target number. It is the weaker filter. The main thing it can be used for is to conveniently divide the initial set into 2 subsets (for instance positive and negative after sorting). So it is an interesting вАЬsplit pointвАЭ that can be useful in some cases. In fact you can divide it at any number, but if it is not the target number you will lose some of the filtering power of this number. In fact some of algorithms are doing exactly this, but just because the вАЬprofitвАЭ from the other split is bigger than the loss from this. Anyway this is not so important issue, now we are on the matter of target value.
As we said above dividing the set to subsets is very useful because this way we can lower the complexity to calculate all possible combinations in each of the 2 subsets. For instance, if 2 subsets are equal, then we will have complexity lowered from O(2n) to (2*2n/2). If they are not equal we will have different reductions in each of 2 subsets.
Why the target number is interesting? The answer is because it splits a hypothetically sorted set of numbers to 2 subsets that does not need to calculate the combinations of numbers that are only from one of the sides of the target number. I.e. if the split is on positive and negative numbers and the target is 0, then you donвАЩt need to check all combinations containing only positive or only negative numbers. You will save much of the time of your processor.
Anyway the target number as filtering factor is not so important. Sometimes it can be вАЬmore profitableвАЭ to split at any other number.
Once we have 2 subsets, theoretically we can go back to initial version by making each-with-each combination and then the complexity will go back to O(2n).
And here it comes the second filter вАУ the value of the current combination. Using it we can prevent part of exactly this вАЬgoing backвАЭ. In fact, we will really go back as we will have to check many combinations that contain members of both 2 subsets. But using the вАЬcurrent valueвАЭ we can avoid part of the job.
So what is the вАЬfiltering powerвАЭ of current value?
Generally we can benefit in 2 ways вАУ by filtering final calculated values of other combinations, or by filtering the initial numbers that start creating combinations and also already calculated combinations from which next level of combinations descend.
These are 2 different approaches that are used in different algorithms. In this article I will not talk about any algorithm, nor focus on inventing algorithms. I am only analyzing the limits of filters that are one or another way implemented in these algorithms.
In filtering against final calculated values of other combinations, using the current value of current combination can be very powerful. If the subsets are sorted the current value can filter almost all useless combinations. Imagine a set of 1000 calculated positive values that are sorted. You have a negative current value. So you can theoretically filter (by some type of genius algorithm) all, or almost all, the values that are not equal to your current value. So the theoretical filtering power of current value is close to 100% when used against other calculated values that are sorted.
Anyway in this case the computer power will have to go to calculating other values and sorting them. In the case of a set divided in 2 subsets, we will have O(2n/2) for creating each subset plus some logarithmic cost of sorting. So if we want to use this extreme filtering power we will have to вАЬinvestвАЭ in initial calculations for creating subsets. If they are equal the complexity will be O(2n/2). But if we have unequal as size subsets then we risk increasing the complexity to the one of the bigger of the 2 subsets (for instance O(2n/4)- small and O(23n/4)-big).
So we come to the second approach. We can use the filtering power of current calculated value to filter combinations before they are calculated. For instance with current calculated value of -5 and a target of 0, we can filter all combinations that are based on positive numbers larger than 6. This means all 1-number possibilities and all 2,3,4вА¶n combinations that descend from 6 and upper numbers. In addition we can on next step filter all 2-number combinations that exceed value of 5. For instance we will check the number 2, but will filter the combination вАЬ2+4вАЭ and all consecutive combinations. And so on.
All this can be done if we are using some type of tree-building algorithm with any new combination coming from the previous one. Combined with initially sorted set (or subset), this filtering can be very impressive as a size. And we donвАЩt forget that in this case we have not still invested computer power in calculating all-possible-combinations.
But what is the limit of this filtering before calculating? In fact the calculation is not complex. In this case the dependency is something like вАЬlinearвАЭ. Not exactly linear because the function is based on discrete numbers and is not uninterrupted. But generally the calculations are the same. The number of calculations that can be filtered and avoided of calculating is depending on the absolute size of the current calculated value. If it is very low and has a low absolute value of the proportion of this value and maximal theoretic value for the subset, then we will be able to filter almost all of the combinations. Imagine current value of -2 and 1000 positive numbers in subset of positives with 999 numbers higher than 2. You will be able to filter 99,9% of all these combinations.
But look at the other side. Imagine current calculated value of -10000 and 1000 positive numbers with 999 of them lower than 10000. You will avoid just 0,01% of combinations. Of course you will have the ability to filter among 2,3вА¶n number combinations. But theoretically if you have a current value that is close to the maximal possible calculated value (as absolute value, it can be negative) then you will be able to filter almost nothing.
So this dependency is something like linear. There are math rules here that lead us to filtering about half of the possible combinations. –Ґhe function is something like:
z=(y(x1)+y(x2)+вА¶+y(xn))/n
y(x)=(x/constant1)*constant2.
Where
z вАУ final number of calculated combinations
y - number of checked combinations for a given value of x
x вАУ current calculated value
constant1 вАУ theoretical max calculated value
constant2 вАУ average density of combinations in set
The sum of all members(y) is something like half of the all possible combinations with linear-type function like this.
So is that good and enough?
If you donвАЩt have any initial divide this economy is not so impressive. You will go to O(2n/2). If we try a mixed approach we can calculate all and sort the smaller subset, and then try filtering with the bigger subset. In our previous cate - O(2n/4)- small and O(23n/4)-big). So the optimization will be to a level of O(23n/4/2). Obviously much worse than O(2n/2) with 2 equal as size subsets.
And that is the end. That is all. All possible possibilities are checked. The power to filter the combinations is limited to O(2n/2). And no algorithm based on these three вАЬwormsвАЭ can do better. In fact this is the answer of the question why after 4 decades of searching it is not yet discovered an algorithm better than the one of Horowitz and Sahni*. In fact this algorithm is very close to the theoretically possible lowest level complexity O(2n/2) and any other better algorithm will not bring enormous improvement.
So finally вАУ if the вАЬSubset sum problemвАЭ is proven unsolvable in non-exponential time, and as it is a NP-complete problem, therefore: PвЙ†NP
----------
"–Ч–∞–±.: –Э–∞ 25 —П–љ—Г–∞—А–Є, –≤ –Њ—В–≥–Њ–≤–Њ—А –љ–∞ –њ—А–Њ–≤–µ–ї–Є—В–µ —Б–µ –і–Є—Б–Ї—Г—Б–Є–Є –≤ –Ш–љ—В–µ—А–љ–µ—В, –Ф–Њ–±—А–Є –С–Њ–ґ–Є–ї–Њ–≤ –њ—Г–±–ї–Є–Ї—Г–≤–∞ –љ–∞ –±–ї–Њ–≥–∞ —Б–Є —А–∞–Ј—И–Є—А–µ–љ —Б –њ–Њ–≤–µ—З–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –≤–∞—А–Є–∞–љ—В –љ–∞ —А–µ—И–µ–љ–Є–µ—В–Њ –Є –≥–Њ –њ—А–µ–і—Б—В–∞–≤–Є –Є –љ–∞ –Љ–µ–і–Є–Є—В–µ.
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞
–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
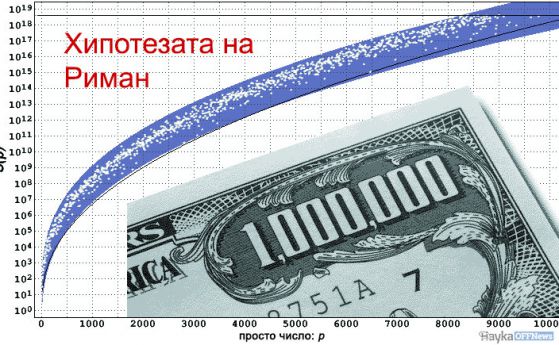
–•–Є–њ–Њ—В–µ–Ј–∞—В–∞ –љ–∞ –†–Є–Љ–∞–љ –Ј–∞ –ї–∞–Є—Ж–Є
–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
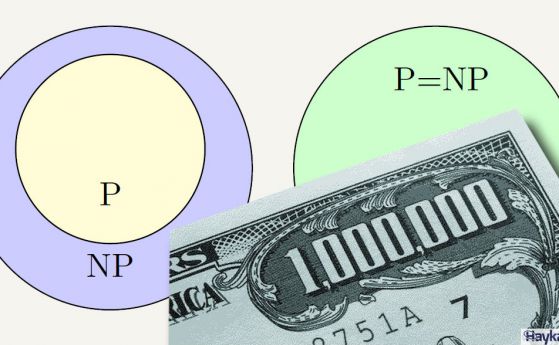
–Р–Ї–Њ P = NP, —З–Њ–≤–µ–Ї —Й–µ –±—К–і–µ –С–Њ–≥

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Э–Є–≥–µ—А–Є–є—Б–Ї–Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї –µ –Ј–∞—П–≤–Є–ї, —З–µ –µ –љ–∞–Љ–µ—А–Є–ї —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞ –Ј–∞ 1 –Љ–ї–љ –і–Њ–ї–∞—А–∞




















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
14005
36
31.12 2017 –≤ 00:14
–° –і–≤–µ –і—Г–Љ–Є, –Ї–Њ–ї–Ї–Њ—В–Њ –њ–Њ–≤–µ—З–µ –Є–Ј—З–Є—Б–ї–µ–љ–Є—П –Є–Ј–≤—К—А—И–≤–∞ –µ–і–Є–љ –Ї–Њ–Љ–њ—О—В—К—А, —В–Њ–ї–Ї–Њ–≤–∞ –њ–Њ-–Љ–∞–ї–Ї–Њ –Є–Ј—З–Є—Б–ї–µ–љ–Є—П –Љ–Њ–ґ–µ –і–∞ –Љ—Г —Б–µ –љ–∞–ї–Њ–ґ–Є –і–∞ –Є–Ј–≤—К—А—И–≤–∞. –Ъ–Њ–≥–∞—В–Њ –Ї–Њ–Љ–њ—О—В—К—А—К—В —В—А—П–±–≤–∞ –і–∞ –њ—А–µ—Б–Љ–µ—В–љ–µ 2—Е3 = ? , –Є –њ—А–Є–µ–Љ–µ–Љ, —З–µ —Е=2 –Є —Г=3, —В–Њ –Ј–љ–∞–Ї—К—В —Е –Љ—Г –Ї–∞–Ј–≤–∞, —З–µ —В—А—П–±–≤–∞ –і–∞ —Б—К–±–µ—А–µ 2 —Б—К—Б —Б–µ–±–µ —Б–Є 3 –њ—К—В–Є, —В.–µ —А–µ—И–µ–љ–Є–µ—В–Њ —Й–µ –±—К–і–µ 2+2+2 = ? –Ъ–Њ–≥–∞—В–Њ –Њ–±–∞—З–µ –љ–Є–µ —А–µ—И–∞–≤–∞–Љ–µ —В–∞–Ї–∞–≤–∞ –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–∞ –Ј–∞–і–∞—З–∞, –љ–Є–µ —Б–Љ–µ –љ–∞–Є–Ј—Г—Б—В–Є–ї–Є –Њ—В–≥–Њ–≤–Њ—А–∞ –њ—А–µ–і–Є.
12.01 2016 –≤ 00:57
–Я–Њ–≤–µ—З–µ—В–Њ —Й–µ —А–µ—И–∞—В –Ј–∞–і–∞—З–∞—В–∞ –Ї–∞—В–Њ –Є–Ј—З–Є—Б–ї—П—В –Љ–∞–Ї—Б–Є–Љ–∞–ї–љ–Є—П –±—А–Њ–є —А–∞–Ј–ї–Є—З–Є–Љ–Є —Б—К—Б—В–Њ—П–љ–Є—П –Ї–Њ–Є—В–Њ —Б–µ –Ї–Њ–і–Є—А–∞—В —Б —В—П—Е –Є —Й–µ —Б–≥—А–µ—И–∞—В.
–Э—П–Љ–∞ –і–∞ –Њ—В—З–µ—В–∞—В, —З–µ –≤—Б—П–Ї–Њ —Б—К—Б—В–Њ—П–љ–Є–µ –Љ–Њ–ґ–µ –і–∞ –µ —З–µ—В–љ–Њ –Є–ї–Є –љ–µ—З–µ—В–љ–Њ, –і–∞ –µ –њ–Њ-–Љ–∞–ї–Ї–Њ –Њ—В 8 –Є–ї–Є –њ–Њ-–≥–Њ–ї—П–Љ–Њ –Є–ї–Є —А–∞–≤–љ–Њ –љ–∞ 8.
–Р–Ї–Њ –±–Є—В–Њ–≤–µ—В–µ —Б–µ –љ–∞—А–µ–і—П—В –≤ –Љ–∞—В—А–Є—Ж–∞ –Њ—В –і–≤–∞ —А–µ–і–∞ –Є –і–≤–µ –Ї–Њ–ї–Њ–љ–Є, –Њ—Б–≤–µ–љ –љ–µ–≥–Њ–≤–Њ—В–Њ —Б—К—Б—В–Њ—П–љ–Є–µ (0 –Є–ї–Є 1) –≤–µ—З–µ –Є–Љ–∞ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П –Є –Ј–∞ –љ–Њ–Љ–µ—А–∞ –љ–∞ —А–µ–і–∞ –Є –Ї–Њ–ї–Њ–љ–∞—В–∞. –°—К—Б—В–Њ—П–љ–Є—П—В–∞ –Љ–Њ–≥–∞—В –і–∞ —Б–µ —А–∞–Ј–≥—А–∞–љ–Є—З–∞—В –Є –њ–Њ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ–љ –њ—А–Є–Ј–љ–∞–Ї, –љ–∞–њ—А–Є–Љ–µ—А –і–∞–ї–Є —А–∞—Б—В–µ—А–Є–Ј–Є—А–∞—В –Њ—В—Б–µ—З–Ї–∞ –Є–ї–Є –љ–µ. –Э—П–Ї–Њ–Є —Й–µ –њ–Њ—Б–Њ—З–∞—В, —З–µ –Є —В–Њ–≤–∞ –µ –Є–Ј–±—А–Њ–Є–Љ–Њ. –Ф–Њ–±—А–µ, –∞ –Ї–∞–Ї–≤–Њ —Й–µ –Ї–∞–ґ–∞—В –Ј–∞ —В–Њ–≤–∞: –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –Ї–∞—А—В–Є–љ–∞ –њ–Є—Б–∞—В–µ–ї –≤–Є–ґ–і–∞ —Б—О–ґ–µ—В–∞ –Ј–∞ –љ–Њ–≤–∞—В–∞ —Б–Є –Ї–љ–Є–≥–∞, –≤ –і—А—Г–≥–∞ - –Ї–Њ–Љ–њ–Њ–Ј–Є—В–Њ—А–∞ —Й–µ –њ–Њ—З—Г–≤—Б—В–≤–∞ –љ–Њ—В–Є—В–µ –љ–∞ –љ–Њ–≤–∞—В–∞ —Б–Є –њ–µ—Б–µ–љ, –∞ –≤ —В—А–µ—В–∞ - –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ —Й–µ –Њ—В–Ї—А–Є–µ –љ–Њ–≤–∞ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В. –Ґ–Њ–≤–∞ —Г–Љ–µ–љ–Є–µ —Б–µ –љ–∞—А–Є—З–∞ –∞—Б–Њ—Ж–Є–∞—Ж–Є—П –Є –µ –љ–µ–њ–Њ–і–≤–ї–∞—Б—В–љ–Њ –љ–∞ –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–∞—В–∞. –Ш–љ–і–µ–Ї—Б–Є—А–∞–љ–µ—В–Њ, —Е–µ—И–Є—А–∞–µ—В–Њ –Є —А–µ—З–љ–Є—Ж–Є—В–µ —Б–∞ –Љ–љ–Њ–≥–Њ –і–∞–ї–µ—З–љ–Є –±—А–∞—В–Њ–≤—З–µ–і–Є –љ–∞ –∞—Б–Њ—Ж–Є–∞—Ж–Є—П—В–∞. –° –љ–µ–є–љ–∞ –њ–Њ–Љ–Њ—Й –њ–Њ–≤–µ—З–µ—В–Њ NP-–њ—К–ї–љ–Є –Ј–∞–і–∞—З–Є —Б–µ –њ—А–µ–≤—А—К—Й–∞—В –≤ –ї–Є–љ–µ–є–љ–Є –њ–Њ —Б–ї–Њ–ґ–љ–Њ—Б—В.
11.01 2016 –≤ 13:46
09.01 2016 –≤ 14:18
08.01 2016 –≤ 23:06
–Є–љ–∞—З–µ, –Ї—А–Є—В–Є–Ї–Є—В–µ –љ–∞ '–Ґ–∞–љ–≥' —Б–∞ –љ–∞ –Љ—П—Б—В–Њ –Є –Ї–Њ–љ—Б—В—А—Г–Ї—В–Є–≤–љ–Є
08.01 2016 –≤ 21:27
–Я–Њ–љ–µ–ґ–µ –Є–Љ–∞–Љ–µ –µ–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї–µ–љ –±—А–Њ–є –Ї–∞–љ–і–Є–і–∞—В–Є –Ј–∞ —А–µ—И–µ–љ–Є—П, –Ј–љ–∞—З–Є –Ј–∞ –і–∞ –≥–Є –њ—А–Њ–≤–µ—А–Є–Љ –≤—Б–Є—З–Ї–Є—В–µ –љ–Є –µ –љ—Г–ґ–љ–Њ –љ–µ-–њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ. –Х–Љ–Є –±—А–∞–≤–Њ, —В–Њ–≤–∞ –µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ—В–Њ –Ј–∞ NP –њ—А–Њ–±–ї–µ–Љ.
08.01 2016 –≤ 17:42
07.01 2016 –≤ 18:01
–°–њ–µ—Ж–Є–∞–ї–љ–Њ –Ј–∞ —В–∞–Ј–Є –Ј–∞–і–∞—З–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –њ—Б–µ–≤–і–Њ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–µ–љ –∞–ї–≥–Њ—А–Є—В—К–Љ (–љ–µ –ї–Є–љ–µ–µ–љ), —В.–µ. —В–∞–Ї—К–≤ –і–µ—В–Њ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ—Б—В—В–∞ –Љ—Г –Ј–∞–≤–Є—Б–Є –љ–µ –Њ—В –±—А–Њ—П –љ–∞ –≤—Е–Њ–і–љ–Є—В–µ –і–∞–љ–љ–Є, –∞ –Њ—В —А–∞–Ј–Љ–µ—А–∞ –Є–Љ (–њ—А–Є–Љ–µ—А–љ–Њ), –∞–Љ–∞ –љ–µ –Љ–Є —Б–µ –Њ–±–µ—Б–љ—П–≤–∞ –њ–Њ–≤–µ—З–µ!
–©–Њ –њ–Є—И–µ—В–µ —В–Њ–ї–Ї–Њ–Ј –≥–ї—Г–њ–Њ—Б—В–Є ?
07.01 2016 –≤ 17:05
07.01 2016 –≤ 10:39
–†–∞–Ј–±–Є—А–∞–Љ –≥–Є –њ—А–Њ—Д–µ—Б–Њ—А–Є—В–µ –і–µ—В–Њ —Б–∞ —Б–µ —И–µ–≥—Г–≤–∞–ї–Є, –і–∞ —В–Є –Ї–∞–ґ–∞ –љ–µ –µ –Є –ї–µ—Б–љ–Њ –Њ—В –Ї—К–і–µ –і–∞ –њ–Њ—З–љ–µ —З–Њ–≤–µ–Ї –і–∞ –і—А–∞—Б–Ї–∞ —Б —З–µ—А–≤–µ–љ–Є—П —Е–Є–Љ–Є–Ї–∞–ї.
–Т–Є–ґ, –њ—А–Њ—Б—В–Њ –љ–µ —Б–µ –Ј–∞–љ–Є–Љ–∞–≤–∞–є, –љ—П–Љ–∞ –і–∞ –≥–Њ —Б–њ–µ—З–µ–ї–Є—И —В–Њ—П –Љ–Є–ї–Є–Њ–љ.
–©–µ —В–Є –≥–Њ –і–Њ–Ї–∞–ґ–∞ –≤ —В–≤–Њ–є —Б—В–Є–ї: –Р–Ї–Њ –Љ–Њ–ґ–µ—И–µ –і–∞ —Б–µ –і–Њ–Ї–∞–ґ–µ –±–µ–Ј —Ж–µ–ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –∞–њ–∞—А–∞—В, –Ї–Њ–є—В–Њ –љ—П–Љ–∞—И, —Й–µ—И–µ –≤–µ—З–µ –і–∞ –µ –і–Њ–Ї–∞–Ј–∞–љ–Њ, –∞ —В–Њ –љ–µ –µ –і–Њ–Ї–∞–Ј–∞–љ–Њ, –Ј–љ–∞—З–Є –љ–µ –Љ–Њ–ґ–µ. –Ґ.–µ. —В–Є—З–∞–є –і–∞ –Ј–∞–њ–Є—И–µ—И –µ–і–љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –Є–ї–Є –Є–љ—Д–Њ—А–Љ–∞—В–Є–Ї–∞ –≤—К–≤ –§–Ь–Ш –Є –њ–Њ—Б–ї–µ –њ—А–Њ–±–≤–∞–є.
–Р –Ї–∞–ґ–Є –Љ–Є —Б–µ–≥–∞ –Ї—К–і–µ –±—К—А–Ї–∞–Љ, —Б–Є–≥—Г—А–љ–Њ –±—К—А–Ї–∞–Љ, –∞–Љ–∞ –љ–µ –Ј–љ–∞–Љ –Ї—К–і–µ!
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
–•—А–Є—Б—В–Є—П–љ–Є–љ
–Ґ–Њ–≤–∞ –µ –Ї—А–∞–ї—П—В –љ–∞ —В–Є–Ї–≤–Є—В–µ: –Ґ–Є–Ї–≤–∞—В–∞ –Љ—Г —В–µ–ґ–Є –љ–∞–і –µ–і–Є–љ –µ–і–Є–љ —В–Њ–љ