Почти всеки от нас е бил очарован от идеята как златното сечение се проявява в геометрията на природата и архитектурата, идея, която показва силата на математиката.
Но математикът Крис Бъд (Chris Budd), професор по приложна математика в Университета на Бат, казва:
"И все пак в цялата си кариера по прилагане на математиката в реалния свят попаднах на златното сечение точно два пъти".
В беседа, публикувана в изданието на Университета в Кеймбридж "+plus math magazine", опровергава митологията за божествената пропорция и много от вълнуващите твърдения за златното сечение.
Вероятно мнозина от вас са чували за числото, наречено златно сечение. Той се появява например в книгата и филма „Шифърът на Леонардо“ („The da Vinci Code”) и в много други статии и книги, които имат за цел да покажат колко важна е математиката в реалния свят. Той е описан от много автори като основа на всички красиви модели в природата и понякога се нарича божествена пропорция. Твърди се, че голяма част от изкуството и архитектурата съдържат елементи в пропорции, съгласувани от златното сечение. Например твърди се, че и Партенонът, и пирамидите са в това съотношение. Твърди се също така, че златното сечение се появява в човешкото тяло, например като съотношение на височината на възрастен човек към височината на пъпа му или на дължината на предмишницата към тази на ръката.
Да си припомним какво е "златно сечение"?
Нека започнем с бързо припомняне какво всъщност представлява златното сечение. Той е определен от древногръцкия математик Евклид, както следва. Представете си, че имате отсечка от линии, която бихте искали да разделите на две части. Бихте искали да го разделите по такъв начин, че съотношението между целия сегмент и по-дългото от двете парчета да е същото като съотношението между по-дългото от двете парчета и по-късото. Какво трябва да бъде това съотношение?
Трябва да изберете A и B , така че ( A + B ) / A = A / B .
С малко математика може да се стигне до този израз за съотношението:
Фактът, който φ се определя като съотношение между две дължини, означава, че можете да го търсите, когато гледате нещо, което има сегменти от линии в него - независимо дали това е лице или сграда.
Златното сечение в човешкото тяло
Предполага се, че златното сечение е в основата на много от пропорциите в човешкото тяло. Те включват формата на перфектното лице, а също и съотношението на височината на пъпа към височината на цялото тяло. Всъщност се твърди, че почти всяка част от перфектното човешко лице има връзка към златното сечение.
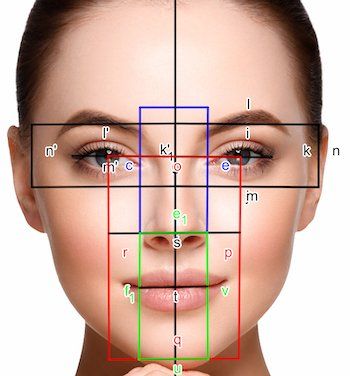
Можете да наслагвате всякакви правоъгълници върху красиво лице и след това да твърдите, че красотата произтича от пропорциите на "златния" правоъгълник.
Нищо от това обаче не е вярно, дори и отчасти. Тялото има много възможни съотношения, много от които се намират някъде между 1 и 2. Ако пресметнете достатъчно от тях, тогава ще получите числа, близки до стойността на златното сечение (около 1.618). Това е особено вярно, ако нещата, които измервате, не са особено добре дефинирани (както е на снимката горе) и е възможно да промените дефиницията по такъв начин, че да получите пропорциите, които искате да намерите.
Ако се вгледате достатъчно, ще намерите пропорции в човешкото тяло, близки до 1.6, 5/3, 3/2, квадратния корен от 2, 42/26 и т.н., и т.н. Всъщност повечето пропорции между 1 и 2 ще имат две части от тялото, които са близки по размер. Подобни фалшиви закономерности се наблюдават и в Слънчевата система (която също има много различни съотношения, от които може да избирате). Също така не забравяйте, че тъй като златното сечение е ирационално число, никога не може да бъде определено точно при измерване.
Всичко това е пример за начина, по който човешкият мозък намира фалшиви корелации. В действителност, като се вземат предвид достатъчно данни, е възможно да се намерят закономерности, които да се съгласуват с почти всяка хипотеза. Един добър начин да видите това е да излезете навън в хубав слънчев ден и да погледнете облаците. Рано или късно ще откриете облак, който отговаря на някакъв образ.
Това явление всъщност може да доведе до опасни заблуди, особено когато се объркат фалшиви корелации с причинно-следствени връзки. По-подробно за това може да прочетете в статията "Слочаенос? Не мисла!".
Спирали, златни правоъгълници и други
Ако вземете линия, разделена на два сегмента A и B така че A/B е златното сечение, и след това оформите правоъгълник със страни A+B и A, тогава този правоъгълник се нарича златен правоъгълник .
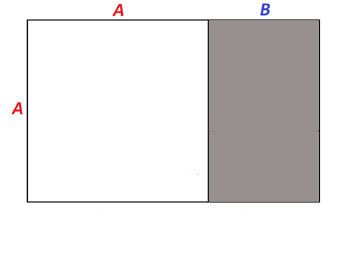Златният правоъгълник се състои от квадрат (бял) и по-малък правоъгълник (сив). По-малкият правоъгълник също е златен правоъгълник.
Златният правоъгълник, който току-що оформихме, се състои от квадрат и по-малък правоъгълник, който сам по себе си е златен правоъгълник. Този златен правоъгълник отново се състои от квадрат и по-малък правоъгълник, който сам по себе си е златен правоъгълник. И така нататък.
Използвайки последователността от по-малки и по-малки златни правоъгълници, можем да образуваме нещо, което прилича на спирала. Просто нарисувайте четвърт кръг във всеки от квадратите, които се появяват в златните правоъгълници.
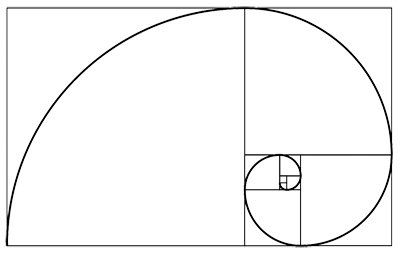
Спирална форма, изградена от златния правоъгълник.
Често се твърди, че тази подобна на спирала форма може да се намери на много места в природата и изкуството. Например, като формата на черупката на наутилус, формата на галактика, формата на ураган или дори на вълна.
Тук има два проблема. Първо, формата не е спирала. Това е последователност от кръгови дъги. Докато преминавате от една дъга към друга, кривината на спиралата скача. Едва ли в някакво природно явление може да се наблюдават подобни скокове. Всъщност формата е само приближение до истинска спирала. Формата на спиралата, на която прилича, е логаритмичната спирала. Такива спирали са много разпространени в природата. Те имат полярното уравнение:
| r = ae bθ, | |||
където e е основата на естествения логаритъм. В природата виждаме такива спирали навсякъде, с различни стойности a и b в зависимост от контекста. Причината тези спирали да са толкова често срещани е, че имат свойството самоподобие. Това означава, че ако завъртите спиралата с някакъв фиксиран ъгъл, тогава ще получите спирала, която е преоразмеряване на оригинала.
Така наречената златна спирала има особената стойност на b,
, където φ е златното съотношение (а ъглите се измерват в радиани).
Изобщо няма причина това число да е по някакъв начин специално. Черупката на наутилуса е логаритмична спирала, тъй като свойството за самоподобност позволява на черупката да расте, без да променя формата си.
Стойностите, b наблюдавани за обвивката на наутилус, нямат връзка с горната стойност, като стойността на b=0.18 се вижда най-често в реалните черупки.
Изкуство и архитектура
Тук трябва да бъдем внимателни. Със сигурност е вярно, че някои творци като Льо Корбюзие (в неговата система Modulor), умишлено са използвали златното сечение в своите произведения на изкуството. Това е така, защото се твърди, че пропорциите на златния правоъгълник са приятни за човешкото око и че естетически предпочитаме златния правоъгълник пред всички останали правоъгълници. Поради това има смисъл да се използват в произведения на изкуството. След това се твърди, че златното сечение може да се види във почти всяко друго произведение на изкуството и архитектурата.
Доказателствата, че златният правоъгълник е особено приятен, са доста несигурни. Психологическите проучвания, показващи различни правоъгълници на групи хора, показват, че е има широк спектър от предпочитания, като съотношението на квадратния корен от две към едно често е предпочитано пред останалите. Изпробвайте се на правоъгълниците отдолу, за да видите кой предпочитате.
Според книгата на Кийт Девлин Ъгълът на Девлин: Митът, който няма да изчезне (Devlin's angle: The myth that won't go away), идеята, че златното сечение има някаква връзка с естетиката, идва предимно от двама души, от които единият е цитиран погрешно, а другият е прибягнал до фантазии. Погрешно цитираният автор е Лука Пачоли, който написва книга, наречена De Divina Proportione ("За божествената пропорция") през 1509 г. Книгата е кръстена на златното сечение, но не пропагандира теория на естетиката, основана на златното сечение, или че то трябва да се прилага към изкуството и архитектурата. Подобна гледна точка е погрешно приписвана на Пачоли през 1799 г.
Пачоли е бил близък приятел с Леонардо да Винчи и често се твърди, че самият Леонардо е използвал златното сечение в картините си. Няма преки доказателства за това. Може би най-известният от тези примери е Витрувианският човек. Пропорциите в тази картина обаче не съвпадат със златното сечение. Всъщност Леонардо само споменава съотношенията на цели числа в своите произведения. Предполагаемите примери за златното сечение, появяващо се на неговите картини, са в същия клас като тези, намиращи съотношението в природата.
Девлин приписва "популяризирането" на златното сечение на Адолф Цайзинг (Adolf Zeising), немски психолог от 19-ти век, който твърди, че златното сечение е универсален закон, който описва "красота и пълнота в сферите на природата и изкуството [...], които проникват като първостепенен духовен идеал, всички структури, форми и пропорции, независимо дали са космически или човешки, органични или неорганични, акустични или оптични". Това е просто пример (както по-горе) за виждане на фалшиви закономерности. Работата на Цайзинг обаче повлиява на много други и постави основите на голяма част от съвременния мит.
Така наречената златна спирала, насложена върху Партенона. Няма доказателства, че златното сечение е играло роля в дизайна на тази сграда. Кредит: Oyvind Solstad, CC BY 2.0.
Друг пример за този мит е твърдението, че златното сечение се проявява в пропорциите на Партенона, част от Акропола в Атина.
Няма доказателства за това в гръцката наука, а идеята, че Партенонът има пропорции, дадени от златното сечение, датира едва от средата на 19-ти век. Освен това фактическите размери на Партенона не дават пропорции, особено близки до златното сечение, освен ако не подберете внимателно правоъгълниците.
Всъщност Партенонът има своя хармоничен външен вид благодарение на хитрото разполагане на линиите, които изглеждат успоредни, но всъщност се сближават или се изкривяват, така че е практически невъзможно да се направят достатъчно точно измервания, за да се дадат точни съотношения. Тъй като пропорциите на Партенона варират в зависимост от височината му, просто не е възможно да се намери обща пропорция, която да е в съгласие със златното сечение.
Същото се отнася и за останалата гръцка архитектура: няма никакви доказателства, че гърците са смятали златното сечение за естетически приятно или изобщо да са го използвали в своето изкуство и архитектура.
Златното сечение в музиката
Златното сечение се прилага и за музиката. Твърди се, че златното сечение е важно за музикалните композиции. Има малко доказателства за това.
Златното сечение в музиката всъщност се отнася до формата, а не до честотата (височината на звука), макар че това не пречи на някои така или иначе да правят музика с настройки, свързани със златното сечение Твърдението е, че ако имате някаква работа с AB форма, A и B частите в идеалния случай ще имат продължителност в златното сечение и т.н., тъй като златното сечение осигурява най-добрия баланс между отделното времетраене или между други характеристики. Твърди се, че пропорцията може да се намери конкретно в музиката на Моцарт.
Всъщност в композицията е важна гамата, а гамата е много тясно свързана с дванадесети корен от 2 или 21/12. Именно това число е в основата на музиката, а не златното сечение.
В 21/12 не е кой знае какво специално число - то е най-вече съвпадение и компромис. "Идеалните" съотношения на височините на звука (честотите) се изразяват в малки цели числа, но са свързани с някои математически проблеми (например факта, че (3/2) 4 ≠ 5) и е било възприето решението да се избере компромисна система с 12 равни стъпки за октава, а не неравномерни стъпки с „по-красиви“ числа или, да речем, различен брой равни стъпки (като 19 или 31).
Кредит: Wikimedia Commons
21/12 определя съотношението на честотата на полутоновете в т.нар. равномерно темпериран строй от дванадесет полутона - и днес е най-често употребявания музикален строй.
Съществува много реална опасност в тези упорити митове за златното сечение. Учениците и много други си изграждат една фалшива реалност, заблуждавайки се за начина, по който работи математиката. Рано или късно те ще открият, че тази реалност е лъжлива и ще загубят вяра в съвсем реалната способност на математиката да обяснява света.
Голямата реалност
Всъщност златното сечение е невероятно число и не се нуждае от всички тези фалшиви твърдения, за да бъде специално.
Първо, нека се обърнем към природните явления, които наистина са свързани със златното сечение. Златното сечение е тясно свързано с прочутия ред на Фибоначи: 1, 1, 2, 3, 5, 8, 13, 21
Числовият ред на Фибоначи със сигурност се проявява в природата, тъй като е свързан както с начина на растеж на популациите, така и с начина, по който се съчетават някои форми. Например редът на Фибоначи може да се види в спиралите на съцветията на слънчогледите, които трябва да съответстват по закономерен начин, и в листата на някои растения, които трябва да се разположат така че да улавят най-много слънчева светлина. В резултат на това е възможно да се наблюдават съотношения, близки до златното сечение, възникващи при определени природни явления
 |
Една от най-впечатляващите прояви на числата на Фибоначи е спиралното подреждане на семената върху питата на слънчогледа и на някои други от семейството на астрите. Както се вижда на снимката вляво, там се образуват две множества от логаритмични спирали:
|
|||
|
Снимка: photosite.ru |
 |
Растението вдясно конкретно илюстрира числата на Фибоначи, като начина му на нарастване повтаря точно родословното дърво на зайците на Фибоначи. Този модел на растеж се среща при много треви и дървета. |  |
Така че наистина е възможно да се види златното сечение в градината и за това има много добри математически причини.
Опит за зайцевъдство
Средновековният търговец-математик Леонардо Фибоначи от Пиза е автор на загубеният трактат "Kнига за абака"(книга за изчисления), който определя развитието математиката в Европа за няколко столетия. Именно в този трактат европейците се запознали с индуските (арабските) цифри.
Днес Леонардо от Пиза е известен благодарение на френския математик Люка, който нарекъл на името на Фибоначи числовата последователност, възникнала в една доста тривиална задачка от легендарния трактат: "Някой си поместил двойка зайци на някакво място, обградено от всички страни със стена, за да разбере колко двойки зайци ще се родят в течение на година, ако природата на зайците е такава, че след месец двойката зайци ще възпроизведе на бял свят друга двойка, а зайците ще могат да раждат други зайчета от втория месец след своето раждане".
 |
Първи месец - 1 двойка новородени |
|
Втори месец - 1 двойка (не се размножават - млади са) |
 |
Трети месец - 1+1=2 двойки |
 |
Четвърти месец - 2+1=3 двойки (потомство може да даде само старата двойка) |
 |
Пети месец - 3+2=5 двойки (само 2 от родилите се на третия месец двойки ще дадат потомство на петия месец) |
На шестия месец- 5+3=8 двойки (защото потомство дават само тези двойки, които са родени на четвъртия месец) и т.н. Ако означим броя двойки зайци на n-тия месец с Fn , то F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21 и т.н. или: Fn=Fn-1+Fn-2 , за всички n>2.
Броят на двойките зайци на n-тия месец е равен на броя Fn-1 двойки зайци от миналия месец плюс броят на родилите се двойки зайци, който съвпада с числото Fn-2 двойки зайци, родили през (n-2)-рия месец (нали само те даваха потомство). Числа Fn, образуващи последователността 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... се наричат "числа на Фибоначи", а самата последователност — ред на Фибоначи.
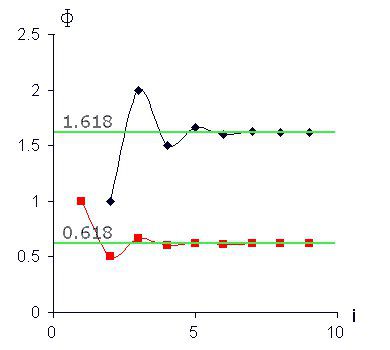
Едно от най-важните свойства на числата на Фибоначи е съществуването на т.н. коефициенти на Фибоначи, т.е. постоянни отношения на различни членове на реда. Те се определят по следния начин:
- Отношението на всяко число към следващото, което се стреми все повече и повече към 0.61803...
- Отношението на всяко число към предишното се стреми към 1.61803... (обратно на 0.618). Числото 1.61803... , по точно
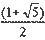, е въпросното ирационално число, наречено златно сечение.
|
 |
Има много очарователни математически свойства на златното сечение, но едно от свойстават му е особено очарователно и наистина отличава златното сечение от останалите числа: неговата изключителна ирационалност.
Ирационалните числа са числа, които не могат да бъдат представени с дроби и цифрите им след десетичната точка продължават безкрайно, без да се повтарят или да показват някаква периодичност. Този факт означава, че е трудно да се наблюдават ирационални числа в природата. Златното сечение има удивителното свойство да бъде най-ирационалното число от всички тях. Това означава, че не само, че не е възможно да се представи точно като дроб, дори не е възможно да се апроксимира лесно с дроб.
Може да се каже, че числото трудно се апроксимира, ако числата в неговата верижна дроб са ограничени (те никога не надвишават някакво фиксирано число) и това е мярка за това колко ирационални са те. Всъщност φ е най-ирационалното число, в неговата верижна дроб никога не надвишава 1:
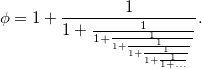
Трудността с апроксимирането на златното сечение с дроб го прави много полезно число за математици и учени, изучаващи процеса на синхронизация. Това се случва, когато система със собствена честота е форсирана от различна честота и приема принудителната честота. Един пример е синхронизирането на човешкия организъм с денонощния ритъм на слънчевата светлина. Друг пример е климатът на Земята, който се синхронизира с естествените цикли на орбитата около Слънцето.
Синхронизацията обаче сама по себе си може да бъде проблем, като доведе до нежелан резонанс в системата (като висящ мост, който вибрира силно и може да се разруши, ако по него преминават маршируващи войници). Избирайки две честоти в съотношение 1:φ, можем да избегнем синхронизацията поради изключителната ирационалност на златното сечение. Това много полезно свойство изглежда се използва от мозъка и различни видове насекоми, както и от климатичните учени и дори от хората, които произвеждат самолети.
Така че златното сечение има важна роля, но не такава, за която сме чели в свързаната с него митология. Това е много жалко. Прекрасен парадокс е, че най-интересното при златното сечение е, че то не е съотношение. То е най-ирационалното число.
За автора
Тази статия се основава на беседа в продължаващата поредица от лекции на колежа „Грешам” на Крис Бъд.
Крис Бъд (Chris Budd) е професор по приложна математика в Университета на Бат, вицепрезидент на Института по приложна математика, председател по математика на Кралския институт и почетен сътрудник на Британската научна асоциация. Той се интересува особено от прилагането на математиката в реалния свят и насърчаване на разбирането на математиката от обществото.
Той е съавтор на популярната математическа книга Mathematics Galore!, публикувана от Oxford University Press.
Източник: Myths of maths: The golden ratio, Chris Budd, plus.maths.org/
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари