Двама математици откриха доказателството за една от най-известните недоказани идеи в математиката, наречена "Хипотезата на простите числа близнаци". Методът, с който намериха това доказателство, макар да е приложен за странни числови пространства, може да помогне да се докаже самата хипотеза.
Хипотезата на простите числа близнаци е свързана с това как и кога прости числа - числа, които са неделими освен на себе си и на 1 - се появяват в числовия ред. "Простите числа близнаци" са прости числа, които са на две стъпки едно от друго по числовата ос: 3 и 5, 5 и 7, 29 и 31, 137 и 139 и т.н. Хипотезата на простите числа близнаци гласи, че има безкрайно много близнаци и че ще продължим да ги срещаме, независимо колко далеч сме стигнали по числовата линия.
Най-известното предсказание на хипотезата на простите числа близнаци е, че има безкрайно много двойки прости числа с разлика 2. Но твърдението е по-общо от това. Той предсказва, че има безкрайно много двойки прости числа с разлика 4 (като 3 и 7) или 14 (293 и 307), или с всякакъв четен интервал.
Алфонс де Полиняк представя хипотезата в сегашния й вид през 1849 г. Математиците постигат нищожен напредък по нея през следващите 160 години. Математиците са почти сигурни, че това е вярно. Изглежда, че е истина. А ако не беше истина, това ще означава, че простите числа не са толкова случайни, колкото си мислим, което би объркало много идеи за това как работят числата като цяло. Но никой не успя да го докаже.
Но през 2013 г. бентът като че ли се отприщи или поне се пропука. През тази година Итан Джан (Yitang Zhang) доказа, че има безкрайно много двойки прости числа с разлика от не повече от 70 милиона. През следващата година други математици, включително Джеймс Мейнард (James Maynard) и Тери Дао (Terry Tao), намалиха интервала значително. Настоящото състояние е доказателството, че има безкрайно много прости числа с разлика най-много 246.
Но напредъкът в хипотезата на простите числа близнаци е в застой. Математиците разбират, че ще им трябва изцяло нова идея, за да разрешат проблема напълно.
И сега математиците може да са по-близо от всякога до успеха. В статия, публикувана на 12 август на сървъра за препринти arXiv, както Quanta magazine за първи път съобщава, двама математици доказаха, че Хипотезата на простите числа близнаци е вярна - поне в някаква алтернативна вселена.
Така правят математиците: вървят към големите доказателства, като доказват по-малки идеи по пътя. Понякога поуките от тези по-малки доказателства могат да помогнат за по-голямото доказателство.
В този случай математиците Уил Сауин (Will Sawin) от Университета Колумбия и Марк Шустърман (Mark Shusterman) от Университета на Уисконсин доказаха версия на хипотезата на простите числа близнаци в алтернативна вселена от „крайни полета“: системи с числа, които не стигат до безкрайност като числовата линия, а вместо това се връщат в началото.
Математика по циферблата на часовника
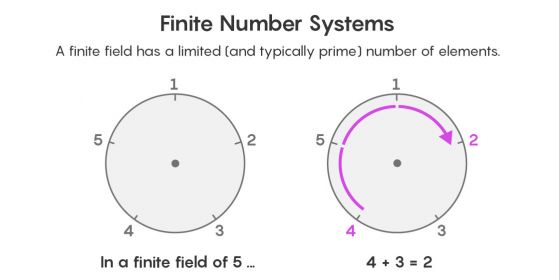
Вероятно всеки ден срещате едно крайно поле като погледнете циферблата на часовника си. Той минава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и извършвайки пълен кръг се завръща обратно на 1. В това крайно поле 3 + 3 все още е равно на 6. Но 3 + 11 = 2.
Вместо да визуализираме числата по числената ос по начина, познат от училище, визуализираме тази нова система с числа в кръг като циферблата на часовник.
Каква ще е аритметиката в такива крайни полета? Какво е 4 + 3 в система с пет елемента? Започваме от 4, пребройте три интервала около циферблата на часовника и ще стигнем до 2. Изваждането, умножението и делението се извършват по подобен начин.
Само че има уловка. Типичното понятие за просто число няма смисъл за крайните полета. В едно крайно поле всяко число се дели на всяко друго число. Например 7 обикновено не се дели на 3. Но в крайно поле с пет елемента се дели. Това е така, защото в това крайно поле 7 е същото число като 12 - и двете се падат на 2 на циферблата на часовника. Така 7 делено на 3 е същото като 12 делено на 3, а 12 делено на 3 е 4.
Поради това хипотезата на простите числа близнаци за крайни полета е за прости полиноми - математически изрази като x 2 + 1.
Например, да кажем, че вашето крайно поле съдържа числата 1, 2 и 3. Полином в това крайно поле би имал тези числа като коефициенти, а „прост“ полином би бил този, който не може да бъде разделен на по-малки полиноми. Така че x 2 + x + 2 е прост, защото не може да бъде разложен на множители, но x 2 - 1 не е прост: той е произведение на ( x + 1) и ( x - 1).
След като имате представата за простите полиноми, естествено е да попитате за двойки прости полиноми - чифт полиноми, които са едновременно прости и се различават с фиксиран интервал. Например полиномът x 2 + x + 2 е прост, както е x 2 + 2 x + 2. Двата се различават с полинома x (добавете x към първия, за да получите втория).
Хипотезата на простите числа близнаци за крайни полета предсказва, че има безкрайно много двойки прости полиноми, които се различават не само по х , но и с какъвто и да е интервал.
Номерът е в разделянето
Крайните полета и простите полиноми може да изглеждат умозрителни или че са от малка полза при изучаването на числата като цяло. Но те са аналогични на симулаторите на урагани - самостоятелна вселена, която дава представа за явленията в широкия свят.
„Съществува стара аналогия между целите числа и полиномите, която позволява да се трансформират проблемите за целите числа, които са потенциално много трудни, в проблеми за полиноми, които също са потенциално трудни, но евентуално по-проследими“, разказва Шустърман.
Крайните полета стават известни през 40-те години, когато Андре Вейл (André Weil) доказа, че може би най-важният проблем в математиката - хипотезата на Риман - може да се тълкува в задаването на криви над крайни полета (проблем, известен като геометрична хипотеза на Риман). Това доказателство, заедно с поредица от допълнителни предположения, които Вейл направи - предположенията на Вейл - установява крайните полета като богат пейзаж за математическо откритие.
Ключовото прозрение на Вейл бе, че при крайните полета техниките от геометрията могат да се използват с реална сила за отговор на въпроси за числата.
„Това е част от нещата, които са специални за крайните полета. Много проблеми, които искате да решите, можете да ги префразирате геометрично“, отбелязва Шустърман.
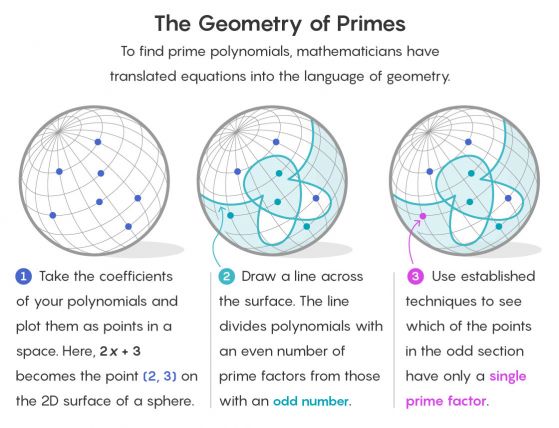
За да видите как възниква геометрията в такава среда, представете си всеки полином като точка в пространството. Коефициентите на полинома служат като координати, които определят къде се намира полиномът. Връщайки се към крайното ни поле от 1, 2 и 3, полиномът 2 х + 3 ще бъде разположен в точката (2, 3) в двумерното пространство.
Но дори и най-простото крайно поле има безкраен брой полиноми. Можете да конструираме по-сложни полиноми, като увеличим размера на най-голямата степен на израза. В нашия случай полиномът x 2 - 3 x - 1 ще бъде представен от точка в триизмерното пространство. Полиномът 3 x 7 + 2 x 6 + 2 x 5 - 2 x 4 - 3 x 3 + x 2 - 2 x + 3 ще бъде представен с точка в осеммерното пространство.
В новата работа това геометрично пространство представлява всички полиноми от дадена степен за дадено крайно поле. Тогава въпросът става: Има ли начин да се изолират всички точки, представляващи прости полиноми?
Стратегията на Сауин и Шустърман е да се раздели пространството на две части. Една от частите ще има всички точки, съответстващи на полиноми с четен брой множители. В другата част ще има всички точки, съответстващи на полиноми с нечетен брой множители.
Kredit: Lucy Reading-Ikkanda / Quanta Magazine
Вече това прави задачата по-проста. Хипотезата за простите числа близнаци за крайни полета се отнася до полиноми само с един множител (точно както простото число има един множител - себе си). И тъй като 1 е нечетно, може да изхвърлите частта от пространството с четните множители изцяло.
Номерът е в разделянето. В случай на двуизмерен обект, какъвто е повърхността на сфера, нещото, което го разрязва на две, е едноизмерна крива, точно както екватора разрязва повърхността на Земята наполовина. Пространството с по-големи измерения винаги може да бъде изрязано с обект, който има едно по-малко измерение.
И все пак фигурите с по-малък размер, които разделят пространството на полиноми, не са толкова елегантни, колкото екватора. Те са начертани с математическа формула, наречена функция на Мьобиус, която приема полином като вход и извежда 1, ако полиномът има четен брой прости множители, -1, ако има нечетен брой прости множители, и 0, ако има само повтарящ се множител (16 може да бъде разложен на 2 × 2 × 2 × 2).
Кривите, начертани от функцията на Мьобиус, се извиват причудливо, пресичайки се на много места. Местата, където се пресичат - наречени сингулярности - са особено трудни за анализ (и съответстват на полиноми с повтарящ се прост множител).
Основната иновация на Сауин и Шустърман бе в намирането на точен начин за разрез на нискодименсиалните криви на по-къси сегменти, което улеснява проучването.
След като те каталогизират полиномите с нечетен брой прости множители - най-трудната стъпка - Сауин и Шустърман трябваше да определят кой от тях е прост и кои са близнаци. За да направят това, те прилагат няколко формули, които математиците използват за намиране на простите числа.
Сауин и Шустърман успяха да докажат два основни резултата за простите полиноми в определени крайни полета.
Първо, хипотезата за прости числа близнаци за крайни полета е вярна: Има безкрайно много двойки прости полиноми, разделени от произволно избран интервал.
Второ, и още по-важно следствие, работата дава точния брой на простите полиноми близнаци, които може да има сред полиномите от дадена степен. Аналогично е на това да знаете колко близнаци попадат в рамките на всеки достатъчно дълъг интервал в числовата линия - един вид мечтания резултат за математиците.
„Това е първата работа, която дава количествен аналог на това, което се очаква да бъде вярно за целите числа, и това наистина е забележително“, заяви Зеев Рудник (Zeev Rudnick) от Университета в Тел Авив. "Досега не е имало нещо подобно."
Доказателствата на Сауин и Шустърман показват как близо 80 години след като Андре Вейл доказа хипотезата на Риман в криви над крайни полета, математиците все още енергично следват неговото ръководство. Математиците, преследващи хипотезата на близнаците, ще се обърнат към работата на Сауин и Шустърман и се надяват, че и тя ще им даде същото вдъхновение.
Справка: On the Chowla and twin primes conjectures over Fq[T]
Will Sawin, Mark Shusterman
Източник:
Big Question About Primes Proved in Small Number Systems, Quanta magazine
Mathematicians Solve 'Twin Prime Conjecture' — In an Alternate Universe, Live Science .
Още по темата
Математика
Най-голямото просто число се е увеличило с един и половина милиона знака
Математика
Известен математик твърди, че е доказал 160-годишната хипотеза на Риман
Физика
Изненадващ скрит ред обединява простите числа и квазикристалите
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари