
Още според древните математици най-интересните и съвършени геометрични обекти на нашето пространство са правилните многостени или т.н.
Платоновите тела
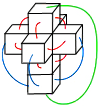
Има много многостени (в действителност, безкраен брой), но само пет от тях са правилни. Основния белег е да имат еднакви стени, с еднаква дължина на страните. Също така във всеки връх да се срещат еднакъв брой ръбове). Тези свойства са достатъчни (почти) за характеризиране на петте обекта, които искаме да покажем на гущерчетата:
| Изображение | Разгъвка | Название | Стени F | Върхове S | Ребра L | Елемент според питаго-рейците |
 |
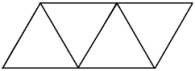 |
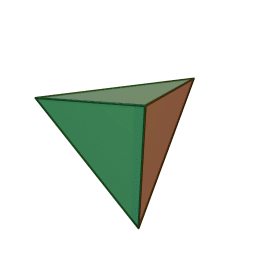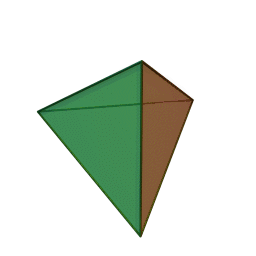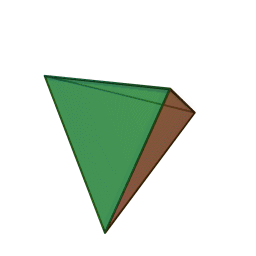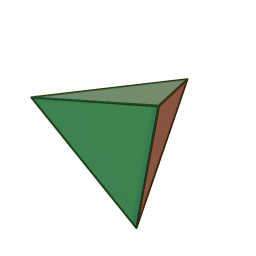
Тетраедър | 4 | 4 | 6 | Огън |
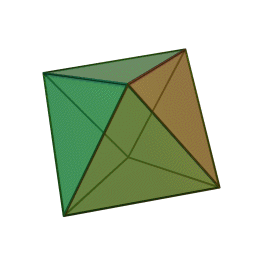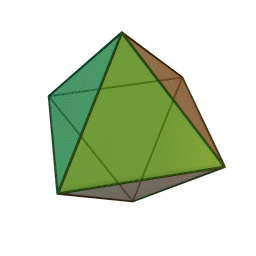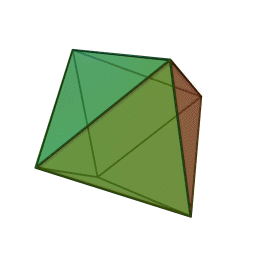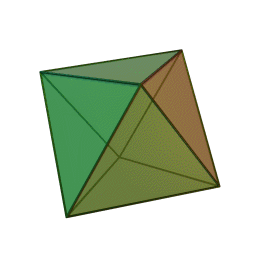 |
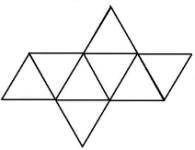 |
Октаедър | 8 | 6 | 12 | Въздух |
 |
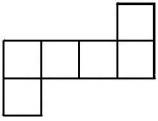 |
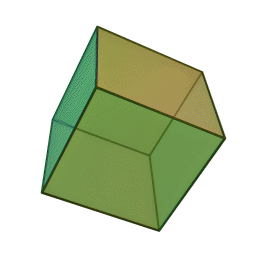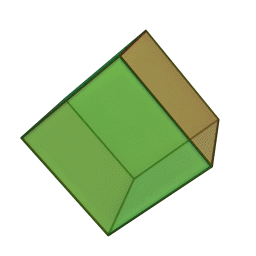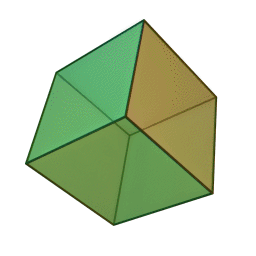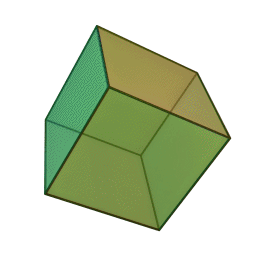
Куб | 6 | 8 | 12 | Земя |
 |
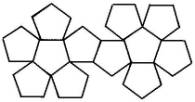 |
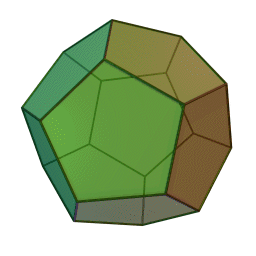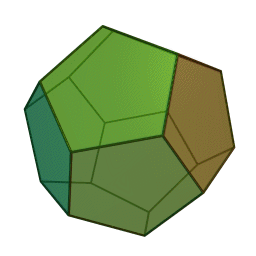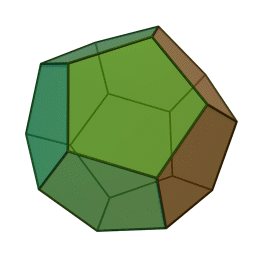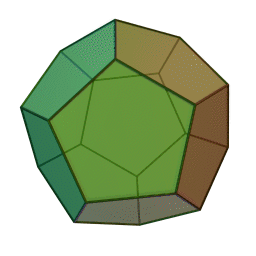
Додекаедър | 12 | 20 | 30 | Етер, Вселена |
 |
 |
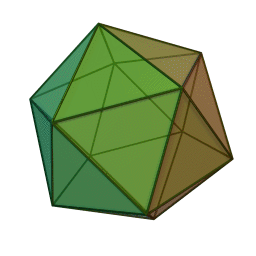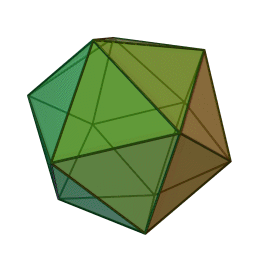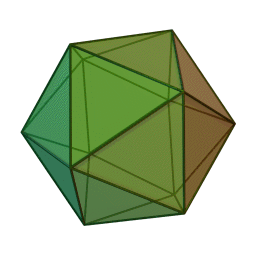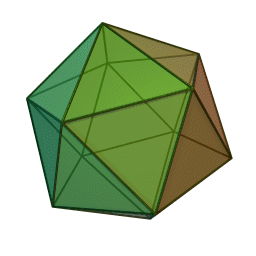
Икосаедър | 20 | 12 | 30 | Вода |
Според Ойлер всяко Платоново тяло трябва да удовлетворява зависимостта:
S - L + F = 2 или F + S = L + 2 ,
където F , L и S са съответно броят на стените, ръбовете и върховете.
Мистичният смисъл, който са придавали на Платоновите тела
Питагорейците смятали за опасно познаването на додекаедъра. Според тях, той е свързан по някакъв мистичен начин с Космоса.
Останалите четири правилни триизмерни фигури са идентифицирани по някакъв начин с четирите „елемента“, за които се смятало, че изграждат света: земя, огън, въздух и вода.
А петата правилна фигура, решават питагорейците, трябва да съответства на някакъв пети елемент - етер (Ether/Aether) или Вселената, който може да бъде символ и на божественото, субстанция на небесните тела. (От тази представа за петата същност произхожда думата квинтесенция).
На обикновените хора не трябвало да бъде давана информация за додекаедъра, свързва се с "тайното", "забранено" и "древно" знание.
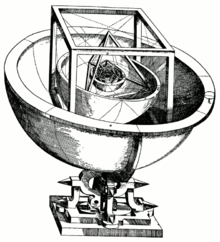
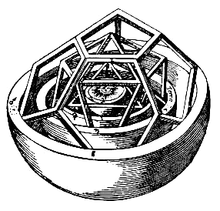
Йохан Кеплер прави в своята "Мистериум Космографикум" изображение на Слънчевата система, в което вписва Платоновите тела (правилни многостенници) в сфери.
Всяко от Платоновите тела е вписано в сфера и може в него да бъде вписана сфера, в която да бъде вписано следващото Платоново тяло. Сферите тогава са орбитите на планетите, а разстоянието между тях се определя от вписаното Платоново тяло.
Така се получават 6 сфери, разделени от 5 Платонови тела. Последователността от вътре на вън е - октаедър, икосаедър, додекаедър, тетраедър и куб. Като елементи подредбата в модела на Кеплер е въздух, вода, етер, огън, земя. Сферите, които ги обхващат отговарят на Меркурий, Венера, Земя, Марс, Юпитер и Сатурн.
В днешни времена Дан Уинтър смята, че формата на вселената е звезден додекаедър. Причината според него е, че тази форма е идеална за претворяване във фрактал и също така е идеалния 3D модел на фрактално електрическо поле.
Платоновите тела от четвъртото измерение
За широката публика четвъртото измерение често напомня за научна фантастика, паранормални явления. Някои твърдят, че там са душите на умрелите, а други поместват там и Боговете. За бедните "флатлендери", тримерно същество, което може да преминава през "стени", да обръща "наопаки" 2D обекти, да се появява и изчезва и пр. фокуси, ще изглежда наистина "всемогъщо". Ето такива приказни възможности носи увеличаването на размерността само с единица. И друго - както ние, тримерните изглеждаме "всемогъщи" за 2D съществата, така биха били всемогъщи спрямо нас и съществата от 4-тото измерение.
Но как поне да "надникнем" в 4 пространството?
От математична гледна точка няма нищо сложно в 4D- пространството. Просто добавяме още една променлива (W. да речем) в уравненията и точката вече ще се определя с четири числа: X, Y, Z, W. Геометрично това се изразява просто с добавяне на още една ос, перпендикулярна на останалите три. Как може да "виждаме" в четвъртото измерение? Все пак има някои начини.
Аналогия
За да се разбере характера на четиримерното пространство, можем да използваме методът на аналогията, т.е изучавайки как се отнасят характеристиките на обектите в (N - 1)-размерното пространство спрямо N - пространството, да си направим извода как (N + 1) -размерното пространството ще се отнасят към N -тото.
| Граници | Сечение | Образуване | Разгъвка | |||
|---|---|---|---|---|---|---|
| 1D |  |
X |  |
 точка точка |
 |
|
| 2D |  |
X, Y | 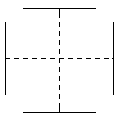 |
 линия линия |
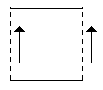 |
 |
| 3D | 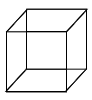 |
X, Y, Z | 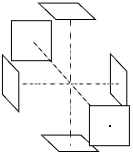 |
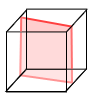 много- ъгълник много- ъгълник |
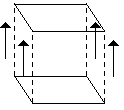 |
 |
| 4D |  |
X, Y, Z, W | 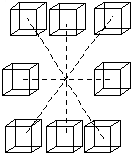 |
сечението е многостен |  |
 |
Ако 2D фигурите са многоъгълници, 3D телата наричаме многостени, то 4D си имат специално име - политопи.
Интересно е, че както сечението на куба може да има по-голяма площ от стените му, така многоъгълникът, получен от пресичане на 4-мерното тяло с 3-мерно пространство, може да е е по-голям от ограждащите го многостени. Представете си как в n-мерен куб с ръб дори сантиметър, може да се събере например нашата планета.
4D Многостените
Швейцарският математик Лудвиг Шлефли (Ludwig Schläfli) е първият, който през 1852 г. класифицира всички правилни политопи в по-високите измерения.Той установява варианта на формула на Ойлер за по-високи измерения.
Шлефли описал правилните политопи, т.е. n-мерните братовчеди на правилните многоъгълници и Платоновите тела.
Аналогично на Платоновите тела, правилни многостени в четвъртото измерение са:
| Просто име | Име | Върхове | Ребра | 2D Стени | 3D Стени |
|---|---|---|---|---|---|
| Симплекс | Пентахор | 5 | 10 | 10 триъгълника | 5 тетраедра |
| Хиперкуб | Тесаракт | 16 | 32 | 24 квадрата | 8 куба |
| 16 (Хипероктаедър) | Хексадекахор | 8 | 24 | 32 триъгълника | 16 тетраедра |
| 24 | Икоситетрахорон | 24 | 96 | 96 триъгълника | 24 октаедра |
| 120 | Хекатоникосахор | 600 | 1200 | 720 петоъгълника | 120 додекаедра |
| 600 | Хексакосизор | 120 | 720 | 1200 триъгълника | 600 тетраедра |
 |
|
||||||
| Ако поставите мишката върху някое име по-горе, ще видите съответстващото му въртящо се 4-мерно тяло. |
Любопитно е, че 4-мерните политопи са с един повече, но за 5-мерното и всички по-висши размерности - са само по 3 - аналозите на куба, тетраедъра и октаедъра.
В този филм ще видите анимации на тези политопи в 4 и 5 измерения. В петото измерение политопите се наричат политери.
Източници:
wikipedia-Four-dimensional space
Introduction to the fourth dimension
Дан Уинтър и формата на вселената























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
06.02 2015 в 01:47
05.02 2015 в 09:38
Някой от много учените може ли да си направи една *** на ума по този въпрос? :Р
Не се заяждам, интересно ми е...
05.02 2015 в 09:34
Последни коментари
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?
Nikor
На 30 септември 1928 е открит пеницилинът