Триъгълникът на Рело - от мехурчета до двигатели с вътрешно горене

Триъгълникът на Рело (Reuleaux) има удивителни свойства. Например свредло, направено с такова сечение, може да пробива квадратни дупки с неточност само 1.2%.

Триъгълникът на Рело се ограничава от пресичането на три кръга с центрове във върховете на равностранен триъгълник и радиуси, равни на негова страна.

Триъгълникът на Рело може да се построи с помощта само на пергел без линийка. Цялото построение се свежда до последователно изчертаване на три равни окръжности. Центърът на първата се избира произволно, центърът на втората е коя да е точка от първата окръжност, а центърът на третата е коя да е от двете пресечни точки на първите две окръжности.

Триъгълникът на Рело е най-простата след кръга фигура с постоянна ширина. Това означава, че ако към един триъгълник на Рело се прекарат двойка успоредни опорни линии, независимо от избраната им посока, разстоянието между тях ще е постоянно. Това разстояние се нарича ширина на триъгълника на Рело.

Триъгълникът на Рело e крива с постоянна ширина. Страната на квадрата са опорните прави: всяка страна се опира до триъгълника, но не го пресича. Триъгълникът на Рело може да се върти и при това винаги ще се опира до всяка страна на квадрата. Така ширината на триъгълника (разстоянието между две опорни прави) ще е постоянна.

История

Немският механик от 19-ти век Франц Рело не е откривател на тази фигура, въпреки че я е изследвал подробно. В частност, той се е занимавал с въпроса колко контакта (кинематични двойки) са необходими да се предотврати движението на тази фигура в равнина и установил, че дори три контакта може да не са достатъчни, за да се гарантира, че няма да не се върти.

Подобна фигура е намерена още през XV век - в ръкописите на Леонардо да Винчи.

Около 1514 Леонардо да Винчи е създал една от първите по рода си карти на света. Повърхността на земното кълбо върху нея се разделя от екватора и два меридиана (ъгълът между равнините на тези меридиани е равен на 90 °) на осем сферични триъгълници, които са показани на равнината на картата като триъгълници на Рело, събрани по четири около полюсите.

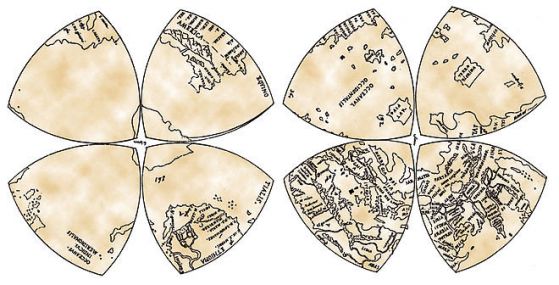
Още по-рано, през XIII век, създателите на църквата на Дева Мария в Брюж са използвали триъгълници на Рело като форма на някои прозорци (снимката най-горе). 

Геометрични характеристики на триъгълника на Рело

Ако ширината на триъгълника е равна на а, то площта му е равна на:

периметърът: 

Въртене в квадрат

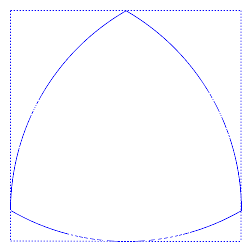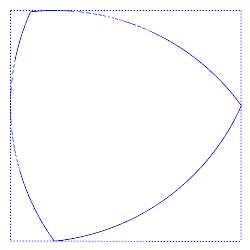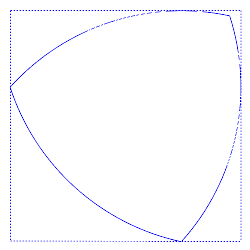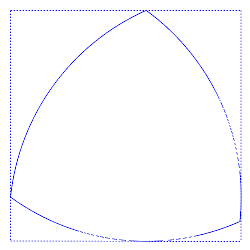
Всяка фигура с постоянна ширина като триъгълника на Рело може да се впише в квадрат със страни, равни на ширината на фигурата, без значение на ориентацията на квадрата. Така вписан триъгълникът на Рело може да се върти в квадрат, постоянно докосвайки всички четири страни.

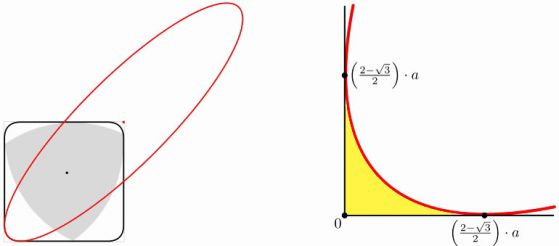
Всеки връх на триъгълника при неговото въртене преминава почти целия периметър на квадрата, отклонявайки се от тази траектория само в ъглите - там връхът описва дъга от елипса, завъртяна на 45° спрямо страните на квадрата.  А оста на триъгълника не описва кръг, както изглежда, а фигура, съставена от 4 дъги на елипса.

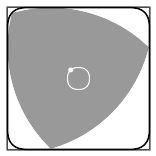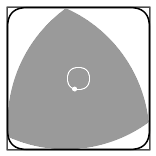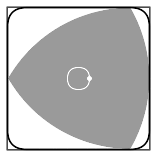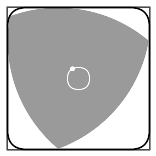
Елипсата в червено, очертава един от ъглите на фигурата (с черна граница), която покрива триъгълника на Рело при въртене в квадрат.	В светложълто е показан незасегнатия от въртенето ъгъл на квадрата

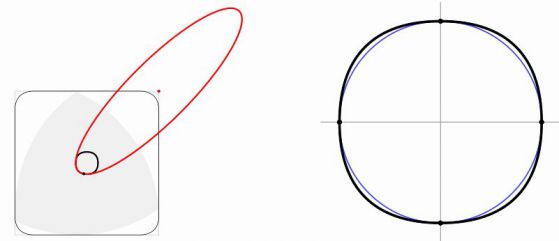
Елипсата в червено, очертава един една четвърт от кривата, по която се движи центърът на триъгълника на Рело при въртене в квадрат.	Траекторията на центъра на триъгълника на Рело при въртене в квадрат. За сравнение е показана окръжност (в синьо).

Разликата с площта на квадрат е ≈1,2%, така че въз основа на триъгълника на Рело се правят свредла, с които може да се получи почти квадратен отвор.

Пробиване на квадратни дупки

Фреза с режещи остриета със сечение във вид на триъгълника на Рело позволява да се получат почти квадратни отвори. Но оста на въртене на такъв изструмент не трябва да стои на едно място, както е при традиционните спирални свредла, а да описва специална крива, състояща се от 4 дъги на елипса. Затова патронникът, към който е прикрепен инструмента не трябва да пречи на това движение.

За първи път да направи подобна конструкциа за закрепване на инструмента успява английският инженер Хари Уотс. Той използвал водеща пластина с отвор във формата на квадрат, в който може радиално да се мести свредло, закрепено в "плаващ патронник". Получава патент през 1917. 

Ванкелов двигател

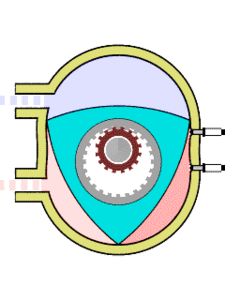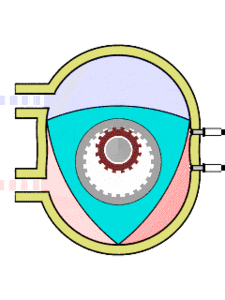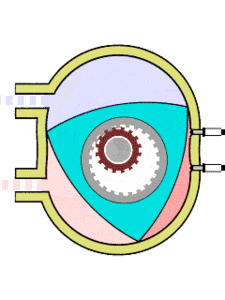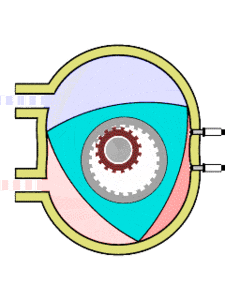Друг пример е двигателят на Ванкел - бутален ротационен двигател с вътрешно горене. Роторът на този двигател е изпълнен във вид на триъгълник на Рело. Той се върти в камера, чиято повърхност е епитрохоида - крива, описана от точка фиксирана спрямо окръжност, която се търкаля по външната страна на друга, направляваща, окръжност. Ако звучи сложно - вижте картинката вляво.

Тристранният ротор обхожда неподвижното зъбно колело, а в същото време допира с върховете си вътрешните стени на двигателя и като образува три области с променлив обем, всяка от които по ред става горивна камера. Така двигателят изпълнява три пълни работни цикъла за един оборот.

Двигателят на Ванкел позволява да се осъществи всеки четиритактов термодинамичен цикъл. Процесите всмукване, сгъстяване, разширение и изпускане са принципно както при обикновените бутални двигатели с вътрешно горене.

Грейферен механизъм

Друго приложение на триъгълника на Рело в механиката е грейферният механизъм, осъществяващ покадрово преместване на лентат в кинопроекторите. Този проектор, например, е основан на триъгълника на Рело, който е вписан в квадратна рамка и закрепен на двоен успоредник (паралелограм). Въртейки се около задвижващия вал, триъгълникът движи рамката с разположените на нея зъбци. Зъбът влиза в перфорацията на кинолентата, дърпа я един кадър надолу и се връща обратно към началото на цикъла.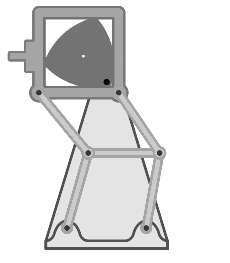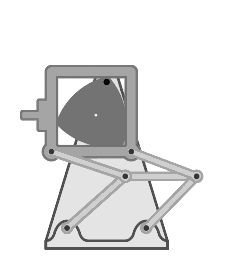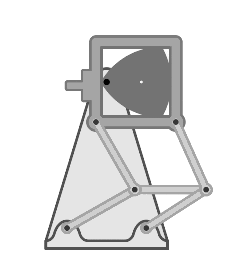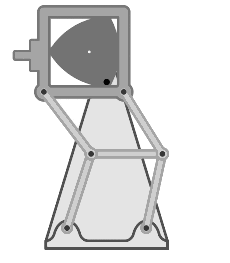

Форма и цвят

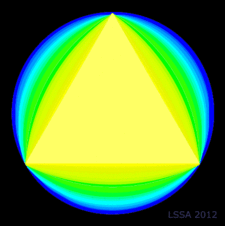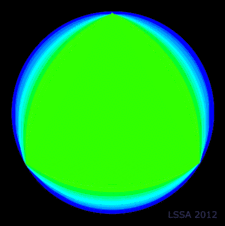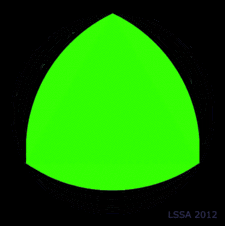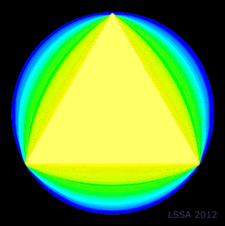Триъгълникът на Рело в съответствията на Й. Итен

Според швейцарския художник и теоретик на изкуствата Йоханес Итен (Johannes Itten) в живописта изразителните свойства на цвета и формата имат съгласувано въздействие.

Трите основни първични цвята: червен, жълт и син съответстват на три основни първични форми: квадрат, триъгълник и кръг.

Зеленият цвят в системата на Итън е "производен" - резултат на смесването на прозрачно-синьо и светложълто, а тъй като в този модел им съответстват кръг и правилен триъгълник. 

Така фигурата, наречена от Итен "сферичен триъгълник" е триъгълникът на Рело и съответства на зеленото.

Триъгълникът на Рело в изкуството

Формата на триъгълника на Рело се среща къде ли не - в дизайна на лога, в архитектурата, дори перцата за китари имат неговата форма.

Сапунените мехури

През 19 век белгийският физик Жозеф Плато на базата на експериментални наблюдения съставя т.н. закони на Плато, описващи структурата на сапунените мехури. Много модели в природата се подчиняват на същите тези закони.

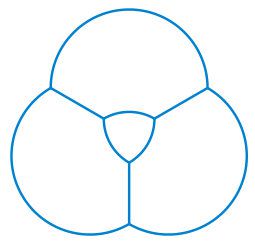Според законите на Плато, кръглите дъги в двуизмерни сапунени балони се срещат под 120° , както ъглите на триъгълника на Рело. Затова се изграждат групи, в които някои от мехурчетата ще са под формата на триъгълник на Рело.