

–°–Ķ—Č–į—ā–Ķ —Ā–Ķ, –Ĺ–į–Ľ–ł ‚Äď –ĺ–Ĺ–∑–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā, –≤ –ļ–ĺ–Ļ—ā–ĺ —Ā—ā–Ķ —Ā–Ľ–ĺ–∂–ł–Ľ–ł —Ā–Ľ—É—ą–į–Ľ–ļ–ł—ā–Ķ –≤ –ī–∂–ĺ–Ī–į —Ā–ł, –ł–∑–≤–į–ī–ł—ā–Ķ –≥–ł –≤ –ľ–Ķ—ā—Ä–ĺ—ā–ĺ —Ā –Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ –ī–į —Ä–į–∑–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–ł—ā–Ķ –Ņ—ä—ā—Ź, –Ĺ–ĺ —Ā–Ķ –Ĺ–į–Ľ–ĺ–∂–ł –ī–į –ł–∑–≥—É–Ī–ł—ā–Ķ –Ķ–ī–Ĺ–į —Ā—ā–į–Ĺ—Ü–ł—Ź –≤—Ä–Ķ–ľ–Ķ –ī–į –≥–ł —Ä–į–∑–Ņ–Ľ–Ķ—ā–Ķ—ā–Ķ. –ó–į—Č–ĺ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į —ā–į–ļ–į?
–Ē—ä–Ľ–≥–ł—ā–Ķ –∂–ł—Ü–ł –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ĺ–ļ–į–∂–į—ā –≤—ä–≤ –≤—Ā—Ź–ļ–į–ļ–≤–ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ł –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ. –ú–ĺ–≥–į—ā –ī–į –Ľ–Ķ–∂–į—ā –≤ –Ĺ–į–≥–Ľ–Ķ–ī –Ņ—Ä–į–≤–į –Ľ–ł–Ĺ–ł—Ź –ł–Ľ–ł –Ĺ–į–Ņ—Ä–ĺ—ā–ł–≤ ‚Äď –ī–į –Ņ—Ä–į–≤—Ź—ā –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ —Ā–ł –ł—Ā–ļ–į—ā –∑–į–≤–ĺ–ł. –ź –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –Ĺ–Ķ–Ņ—Ä–ł—Ź—ā–Ĺ–ĺ –Ķ, –ļ–ĺ–≥–į—ā–ĺ –Ĺ–ł —ā—Ä—Ź–Ī–≤–į—ā –∑–į –Ĺ–Ķ—Č–ĺ –ł —ā–Ķ —Ā–į —Ā–Ķ —Ā–į–ľ–ĺ–∑–į–Ņ–Ľ–Ķ–Ľ–ł.
–ü—Ä–Ķ–∑ 2007 –≥. —Ą–ł–∑–ł—Ü–ł—ā–Ķ –Ē—ä–≥–Ľ–į—Ā –°–ľ–ł—ā (Douglas E. Smith) –ł –Ē–ĺ—Ä–ł–į–Ĺ –†–į–Ļ–ľ—ä—Ä (Dorian Raymer) —Ä–Ķ—ą–ł–Ľ–ł –ī–į –Ņ—Ä–ł–Ľ–ĺ–∂–į—ā —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ –ļ—ä–ľ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł –∂–ł—Ü–ł. –Ę–Ķ –Ņ–ĺ—Ā—ā–į–≤–ł–Ľ–ł –Ņ—Ä–ĺ–≤–ĺ–ī–Ĺ–ł–ļ –≤ –ļ—É—ā–ł—Ź –ł —Ź —Ä–į–∑—ā—ä—Ä—Ā–≤–į–Ľ–ł –≤ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į 10 —Ā–Ķ–ļ—É–Ĺ–ī–ł. –†–į–Ļ–ľ—ä—Ä –Ņ–ĺ–≤—ā–ĺ—Ä–ł–Ľ –ĺ–Ņ–ł—ā–į –ĺ–ļ–ĺ–Ľ–ĺ 3000 –Ņ—ä—ā–ł —Ā –∂–ł—Ü–ł —Ā —Ä–į–∑–Ľ–ł—á–Ĺ–į –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į –ł –ī—ä–Ľ–∂–ł–Ĺ–į, —Ā–ľ–Ķ–Ĺ—Ź–Ľ –ļ—É—ā–ł—Ź—ā–į, –į —Ā—ä—Č–ĺ –ł —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į –ł –Ĺ–į—á–ł–Ĺ–į –Ĺ–į —Ä–į–∑—ā—ä—Ä—Ā–≤–į–Ĺ–Ķ.
–Ď–ł–Ľ–ĺ —É—Ā—ā–į–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ, —á–Ķ –≤ 50% –ĺ—ā —Ā–Ľ—É—á–į–ł—ā–Ķ –∂–ł—Ü–į—ā–į —Ā–Ķ –∑–į–Ņ–Ľ–ł—ā–į, –ĺ–Ī—Ä–į–∑—É–≤–į–Ļ–ļ–ł –≤—ä–∑–Ķ–Ľ. –†–į–∑–Ī–ł—Ä–į —Ā–Ķ, —ā–ĺ–≤–į –ľ–Ĺ–ĺ–≥–ĺ –∑–į–≤–ł—Ā–Ķ–Ľ–ĺ –ĺ—ā –ī—ä–Ľ–∂–ł–Ĺ–į—ā–į –Ļ. –°—Ä–į–≤–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ĺ –ļ—Ä–į—ā–ļ–ł—ā–Ķ –∂–ł—Ü–ł ‚Äď –ī–ĺ 15-–ł–Ĺ–į —Ā–į–Ĺ—ā–ł–ľ–Ķ—ā—Ä–į ‚Äď –Ĺ–Ķ —Ā–Ķ –∑–į–Ņ–Ľ–ł—ā–į–Ľ–ł. –Ě–ĺ —Ā–Ľ–Ķ–ī –Ņ—Ä–Ķ–ľ–ł–Ĺ–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–į –ī—ä–Ľ–∂–ł–Ĺ–į —ā–ĺ–≤–į —Ā—ā–į–≤–į–Ľ–ĺ –Ĺ–Ķ–ł–∑–Ī–Ķ–∂–Ĺ–ĺ.
–ó–į —á–ĺ–≤–Ķ–ļ–į, –ļ–ĺ–Ļ—ā–ĺ –≤—Ā–Ķ–ļ–ł–ī–Ĺ–Ķ–≤–Ĺ–ĺ —Ā–Ķ –∑–į–Ĺ–ł–ľ–į–≤–į —Ā –ļ–į–ļ–≤–ł –Ľ–ł –Ĺ–Ķ –≤—ä–∑–Ľ–ł, —ā–Ķ –ł–ľ–į—ā —Ā–į–ľ–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ī–ł—ā–ĺ–≤ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ. –í –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –ĺ–Ī–į—á–Ķ –≤—ä–∑–Ķ–Ľ—ä—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į –≥–Ľ–į–ī–ļ–į –ļ—Ä–ł–≤–į, –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ĺ –≤–Ľ–ĺ–∂–Ķ–Ĺ–į –≤ —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ł –Ī–Ķ–∑ —ā–ĺ—á–ļ–ł –Ĺ–į —Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ĺ–į—É—á–Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ. –†–į–Ļ–ľ—ä—Ä –ł –°–ľ–ł—ā —Ä–Ķ—ą–ł–Ľ–ł –ī–į –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į—ā –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—ā–Ķ –≤—ä–∑–Ľ–ł –Ņ–ĺ –≤–ł–ī–ĺ–≤–Ķ, —ā–ĺ—á–Ĺ–ĺ –Ĺ–Ķ—Ź –ł –Ņ–ĺ-—Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł—ā–Ķ –Ĺ–į –Ē–∂–ĺ—É–Ĺ—Ā.
–Ě–į—É—á–Ĺ–į—ā–į –ĺ–Ī–Ľ–į—Ā—ā, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ, –ł–∑—É—á–į–≤–į –≤–Ľ–į–≥–į–Ĺ–ł—Ź—ā–į –Ĺ–į –Ķ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł—Ź –≤ —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–ĺ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ.
–Ę–ĺ–≤–į —Ā–į –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ĺ—ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į. –Ę–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –Ķ –Ĺ–į—É–ļ–į –ĺ—ā —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –ł –ł–∑—Ā–Ľ–Ķ–ī–≤–į –Ĺ–į—á–ł–Ĺ–ł—ā–Ķ, –Ņ–ĺ –ļ–ĺ–ł—ā–ĺ —Ą–ł–≥—É—Ä–ł—ā–Ķ —Ā–Ķ –ī–Ķ—Ą–ĺ—Ä–ľ–ł—Ä–į—ā, –Ī–Ķ–∑ –ī–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź—ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ł—ā–Ķ —Ā–ł –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł. –Ę—Ź —Ā–Ķ –∑–į–Ĺ–ł–ľ–į–≤–į —Ā —Ź–≤–Ľ–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–ĺ—Ā—ā, –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ —ā–Ķ–∑–ł, –ļ–ĺ–ł—ā–ĺ –ĺ—Ā—ā–į–≤–į—ā –Ĺ–Ķ–Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ–Ĺ–ł –Ņ—Ä–ł –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł. –§–ĺ—Ä–ľ–ł –ļ–į—ā–ĺ –õ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā, –∑–į –ļ–ĺ—Ź—ā–ĺ –ī—ä–Ľ–≥–ĺ –≤—Ä–Ķ–ľ–Ķ –í–ł –Ņ–ł—ā–į—Ö–ľ–Ķ –ļ–į–ļ–≤–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į, —Ā–į –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –Ĺ–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –≤ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į:

–õ–Ķ–Ĺ—ā–į—ā–į –Ĺ–į –ú—Ć–ĺ–Ī–ł—É—Ā –ł–ľ–į —Ā–į–ľ–ĺ –Ķ–ī–ł–Ĺ —Ä—ä–Ī –ł –Ķ–ī–Ĺ–į –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā, –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –Ĺ–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –Ņ–ĺ—Ā–ĺ–ļ–ł—ā–Ķ –Ľ—Ź–≤–ĺ –ł –ī—Ź—Ā–Ĺ–ĺ. –ú–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ī–ĺ—Ź–ī–ł—Ā–į–Ĺ —Ā —á–Ķ—ā–ļ–į, –Ī–Ķ–∑ —ā—Ź –ī–į —Ā–Ķ –≤–ī–ł–≥–į –ĺ—ā –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā—ā–į –ľ—É.
–ü—Ä–ł–ľ–Ķ—Ä –∑–į –Ķ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ –Ķ –Ņ—Ä–į–≤–į—ā–į, –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į, –Ķ–Ľ–ł–Ņ—Ā–į—ā–į –ł –≤—ä–ĺ–Ī—Č–Ķ –≤—Ā—Ź–ļ–į –Ľ–ł–Ĺ–ł—Ź, —á–ł–ł—ā–ĺ —ā–ĺ—á–ļ–ł, –∑–į–Ķ–ī–Ĺ–ĺ —Ā –ĺ–ļ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—ā–į —Ā–ł –ĺ—ā —Ā—ä—Ā–Ķ–ī–Ĺ–ł —ā–ĺ—á–ļ–ł, —Ā–į –≤–∑–į–ł–ľ–Ĺ–ĺ –Ķ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ł –ł –Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–ł. –ú–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ—ā–ĺ –Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–ĺ–Ķ—ā–ĺ —É—ā–ĺ—á–Ĺ—Ź–≤–į –ł –ĺ–Ī–ĺ–Ī—Č–į–≤–į –∑–į –≤—Ā—Ź–ļ–ĺ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź—ā–į –∑–į –Ľ–ł–Ĺ–ł–ł, –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā–ł (–į –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į), –Ĺ–Ķ—Ā—ä–ī—ä—Ä–∂–į—Č–ł –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ł —ā–ĺ—á–ļ–ł (–Ī–Ķ–∑ —ā–ĺ—á–ļ–ł –Ĺ–į —Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ, –ļ—Ä–į–Ļ–Ĺ–ł —ā–ĺ—á–ļ–ł –ł –ī—Ä.). –ü–ĺ —ā–į–∑–ł —ā–Ķ–ľ–į –ľ–ĺ–∂–Ķ—ā–Ķ –ī–į –≤–ł–ī–ł—ā–Ķ —Ā—ā–į—ā–ł—Ź—ā–į "–•–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ - –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–į—ā–į –Ĺ–Ķ—Ä–Ķ—ą–ł–ľ–į –∑–į–ī–į—á–į".¬†
–ó–į –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł–ľ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ—ā–ĺ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –Ĺ–Ķ–ļ–į –Ņ—ä—Ä–≤–ĺ –ĺ–Ī—Ź—Ā–Ĺ–ł–ľ –ļ–į–ļ–≤–ĺ –Ķ –≤–Ķ–ļ—ā–ĺ—Ä. –ü—Ä–ł–ľ–Ķ—Ä –∑–į –≤–Ķ–ļ—ā–ĺ—Ä –Ķ –Ĺ–į—Ā–ĺ—á–Ķ–Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į, –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –Ķ–ī–ł–Ĺ–ł—Ź—ā –ļ—Ä–į–Ļ –Ķ –Ņ—Ä–ł–Ķ—ā –∑–į –Ĺ–į—á–į–Ľ–ĺ, –į –ī—Ä—É–≥–ł—Ź—ā –∑–į –ļ—Ä–į–Ļ. –ü–ĺ–Ĺ–į—á–į–Ľ–ĺ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤ –≤–Ķ–ļ—ā–ĺ—Ä –Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ–Ĺ –ĺ–Ī–Ķ–ļ—ā, –ļ–ĺ–Ļ—ā–ĺ –ł–ľ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į (–ł–Ľ–ł –ī—ä–Ľ–∂–ł–Ĺ–į) –ł –Ņ–ĺ—Ā–ĺ–ļ–į –ł –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ī–ĺ–Ī–į–≤–Ķ–Ĺ –ļ—ä–ľ –ī—Ä—É–≥–ł –≤–Ķ–ļ—ā–ĺ—Ä–ł, —Ā—ä–≥–Ľ–į—Ā–Ĺ–ĺ —Ā –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–į—ā–į –į–Ľ–≥–Ķ–Ī—Ä–į.
–ē–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ķ –≤–ł–ī –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –≤ –ļ–ĺ–Ķ—ā–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź—ā–į –ī—ä–Ľ–∂–ł–Ĺ–į –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į –ł –≥–ĺ–Ľ–Ķ–ľ–ł–Ĺ–į –Ĺ–į —ä–≥—ä–Ľ –ľ–Ķ–∂–ī—É –ī–≤–į –≤–Ķ–ļ—ā–ĺ—Ä–į. –ē–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —Ā—ä–ī—ä—Ä–∂–į –≤ —Ā–Ķ–Ī–Ķ —Ā–ł —ā—Ä–ł –≤–ł–ī–į –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł—Ź ‚Äď —ā—Ä–ł–ľ–Ķ—Ä–Ĺ–ł, –ī–≤—É–ľ–Ķ—Ä–Ĺ–ł –ł —Ā–Ņ–ĺ–ľ–Ķ–Ĺ–į—ā–ł—ā–Ķ –Ņ–ĺ-–≥–ĺ—Ä–Ķ –Ķ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł.
–ė —ā–į–ļ–į, –ī–ĺ–ļ—ä–ī–Ķ —Ā—ā–ł–≥–Ĺ–į—Ö–ľ–Ķ? –ó–į –ļ–Ľ–į—Ā–ł—Ą–ł–ļ–į—Ü–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ —Ā–Ķ —Ā—ä—Ā—ā–į–≤—Ź—ā —ā–į–Ī–Ľ–ł—Ü–ł ‚Äď —Ā–Ņ–ł—Ā—ä—Ü–ł —Ā –ī–ł–į–≥—Ä–į–ľ–ł—ā–Ķ –Ĺ–į –≤—Ā–ł—á–ļ–ł –Ņ—Ä–ĺ—Ā—ā–ł –≤—ä–∑–Ľ–ł, –ī–ĺ–Ņ—É—Ā–ļ–į—Č–ł –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź –≤—ä—Ä—Ö—É –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā.
–ź —Ā–Ķ–≥–į –ī–į —Ā–Ķ –≤—ä—Ä–Ĺ–Ķ–ľ –ļ—ä–ľ –ī–≤–į–ľ–į—ā–į —Ą–ł–∑–ł—Ü–ł. –°–Ľ–Ķ–ī –≤—Ā—Ź–ļ–ĺ —Ä–į–∑–ļ–Ľ–į—Č–į–Ĺ–Ķ –Ĺ–į –ļ—É—ā–ł—Ź—ā–į —ā–Ķ –∑–į—Ā–Ĺ–Ķ–ľ–į–Ľ–ł –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź –≤—ä–∑–Ķ–Ľ –ł –≤—ä–≤–Ķ–∂–ī–į–Ľ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –≤ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä. –°—ä–∑–ī–į–ī–Ķ–Ĺ–į –ĺ—ā —ā—Ź—Ö –Ņ—Ä–ĺ–≥—Ä–į–ľ–į –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į–Ľ–į —Ą–ł–≥—É—Ä–ł—ā–Ķ. –í —Ä–Ķ–∑—É–Ľ—ā–į—ā –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —É—Ā–Ņ–Ķ–Ľ–ł –ī–į –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į—ā 14 –Ĺ–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ł –≤—ä–∑–Ķ–Ľ–į, –Ņ—Ä–Ķ–ī—Ā–ļ–į–∑–į–Ĺ–ł –ĺ—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—ā–į —ā–Ķ–ĺ—Ä–ł—Ź –ł —Ā—ä—Ā—ā–ĺ—Ź—Č–ł —Ā–Ķ –ĺ—ā —Ā–Ķ–ī–Ķ–ľ –ł –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź. –†–į–∑–Ī–ł—Ä–į —Ā–Ķ, –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ņ–ĺ-–Ņ—Ä–ĺ—Ā—ā –Ī–ł–Ľ –Ķ–ī–ł–Ĺ –≤—ä–∑–Ķ–Ľ, —ā–ĺ–Ľ–ļ–ĺ–≤–į –Ņ–ĺ-—á–Ķ—Ā—ā–ĺ —Ā–Ķ —Ā—Ä–Ķ—Č–į–Ľ. –Ď–ł–Ľ–ł –∑–į–Ī–Ķ–Ľ—Ź–∑–į–Ĺ–ł, –ĺ–Ī–į—á–Ķ, –ł –Ņ–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł –≤—ä–∑–Ľ–ł, —Ā –Ņ–ĺ 11 –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź.
–Ě–į –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į –Ĺ–į —ā–Ķ–∑–ł –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł—Ź –ī–≤–į–ľ–į—ā–į —Ą–ł–∑–ł—Ü–ł —Ā—ä–∑–ī–į–Ľ–ł —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ–Ĺ –ľ–ĺ–ī–Ķ–Ľ –Ĺ–į –∑–į–Ņ–Ľ–ł—ā–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –∂–ł—Ü–ł. –Ę—Ź —Ā–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–≤–į –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł—Ź —Ą–į–ļ—ā, —á–Ķ –∑–į –ī–į —Ā–Ķ —Ā—ä–Ī–Ķ—Ä–Ķ –ī—ä–Ľ–≥–į—ā–į –∂–ł—Ü–į –≤ –ļ—É—ā–ł—Ź—ā–į, –Ķ –Ĺ—É–∂–Ĺ–ĺ –ī–į —Ā–Ķ –Ĺ–į–≤–ł–Ķ, —ā–į–ļ–į —á–Ķ –Ķ–ī–Ĺ–ł —Ā–Ķ–≥–ľ–Ķ–Ĺ—ā–ł —Ā–Ķ –ĺ–ļ–į–∑–≤–į—ā –Ņ–į—Ä–į–Ľ–Ķ–Ľ–Ĺ–ĺ —Ā—ā–ĺ—Ź—Č–ł —Ā–Ņ—Ä—Ź–ľ–ĺ –ī—Ä—É–≥–ł. –ü—Ä–ł —Ä–į–∑—ā—ä—Ä—Ā–≤–į–Ĺ–Ķ—ā–ĺ –ł –ľ–Ĺ–ĺ–≥–ĺ–ļ—Ä–į—ā–Ĺ–ĺ—ā–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä—ä—Č–į–Ĺ–Ķ –Ĺ–į –ļ—É—ā–ł—Ź—ā–į —Ā–Ķ –ļ—Ä—ä—Ā—ā–ĺ—Ā–≤–į—ā –ł —Ā–Ķ –≤–Ņ–Ľ–ł—ā–į—ā –Ķ–ī–ł–Ĺ –≤ –ī—Ä—É–≥, –ĺ—ā–Ĺ–ĺ–≤–ĺ –ł –ĺ—ā–Ĺ–ĺ–≤–ĺ.
–ē—ā–ĺ –ł —Ā—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –ľ–ĺ–ī–Ķ–Ľ–į:

–Ě–ĺ —ā–ĺ–≤–į –Ľ–ł –Ķ –≤—Ā–ł—á–ļ–ĺ? –ö–į–ļ–≤–ĺ —Ā—ā–ĺ–ł –∑–į–ī –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ?
–°—ā—Ä–ĺ–Ķ–∂—ä—ā –Ĺ–į –ľ–į—ā–Ķ—Ä–ł—Ź—ā–į
–ö–į–ļ—ā–ĺ –ľ–Ĺ–ĺ–≥–ĺ —Ā–≤–ĺ–ł –ļ–ĺ–Ľ–Ķ–≥–ł, –ł—Ä–Ľ–į–Ĺ–ī—Ā–ļ–ł—Ź—ā —Ą–ł–∑–ł–ļ —Ā—ä—Ä –£–ł–Ľ—Ź–ľ –Ę–ĺ–ľ—Ā—ä–Ĺ, –Ľ–ĺ—Ä–ī –ö–Ķ–Ľ–≤–ł–Ĺ (William Thomson, Lord Kelvin) –Ņ—Ä–Ķ–∑ –•–Ü–• –≤–Ķ–ļ —Ä–į–∑—Ā—ä–∂–ī–į–≤–į–Ľ –ļ–į–ļ –Ķ —É—Ā—ā—Ä–ĺ–Ķ–Ĺ —Ā–≤–Ķ—ā—ä—ā –ł –ĺ—ā –ļ–į–ļ–≤–ĺ —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ľ–į—ā–Ķ—Ä–ł—Ź—ā–į. –í —ā–ĺ–∑–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ī–≤–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ł —ā–Ķ–ĺ—Ä–ł–ł –∑–į —ā–ĺ–≤–į: –ļ–ĺ—Ä–Ņ—É—Ā–ļ—É–Ľ—Ź—Ä–Ĺ–į –ł –≤—ä–Ľ–Ĺ–ĺ–≤–į. –Ě–ĺ –Ę–ĺ–ľ—Ā—ä–Ĺ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ —ā—Ä–Ķ—ā–ł –≤–į—Ä–ł–į–Ĺ—ā ‚Äď –į—ā–ĺ–ľ–Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź, –≤ –ļ–ĺ—Ź—ā–ĺ –į—ā–ĺ–ľ–ł—ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—ā –ľ–į–Ľ–ļ–ł –Ņ—Ä–Ķ–Ņ–Ľ–Ķ—ā–Ķ–Ĺ–ł –≤—ä—Ä–≤–ł, —ā–ĺ–Ķ—Ā—ā –≤—ä–∑–Ľ–ł.
–Ę–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–ł–Ľ, —á–Ķ —Ä–į–∑–Ľ–ł—á–Ĺ–ł—ā–Ķ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ĺ–ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—ā –Ĺ–į —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –ł —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł—ā–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ĺ–į –į—ā–ĺ–ľ–ł—ā–Ķ. –ó–į—ā–ĺ–≤–į –Ķ –Ĺ—É–∂–Ĺ–ĺ –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ —Ā–Ķ –ľ–ĺ–∂–Ķ –Ņ–ĺ-–Ī—ä—Ä–∑–ĺ —á–ĺ–≤–Ķ—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ī–į —Ā—ä—É–ľ–Ķ–Ķ –ī–į –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į –≤—ä–∑–Ľ–ł—ā–Ķ –ł –ī–į –ľ–ĺ–∂–Ķ –ī–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź –ļ–ĺ–≥–į –ī–≤–Ķ –Ĺ–ł—ą–ļ–ł, –Ĺ–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī –∑–į–Ņ–Ľ–Ķ—ā–Ķ–Ĺ–ł –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ, —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—ā –Ĺ–į –Ķ–ī–Ĺ–į –ł —Ā—ä—Č–į —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–į –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź. –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –Ę–ĺ–ľ—Ā—ä–Ĺ –Ĺ–Ķ –Ņ—Ä–Ķ–∂–ł–≤—Ź–Ľ–į –ľ–Ĺ–ĺ–≥–ĺ, –Ĺ–ĺ –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ī–ł–Ľ–ĺ –Ņ–ĺ—Ā—ā–į–≤–Ķ–Ĺ–ĺ.
–Ę—Ä–ł–≤–ł–į–Ľ–Ķ–Ĺ –≤—ä–∑–Ķ–Ľ
–í –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ķ–ī–Ĺ–į –≥–Ľ–į–≤–Ĺ–į –∑–į–ī–į—á–į ‚Äď –ī–į —Ā–Ķ —Ä–į–∑–Ī–Ķ—Ä–Ķ –ļ–ĺ–≥–į –ī–≤–į –Ĺ–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī —Ā—ä–≤—ä—Ä—ą–Ķ–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ł –≤—ä–∑–Ķ–Ľ–į —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—ā –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ. –° –ī—Ä—É–≥–ł –ī—É–ľ–ł, –Ķ–ī–ł–Ĺ –≤—ä–∑–Ķ–Ľ –ī–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–ł –ĺ—ā –ī—Ä—É–≥ —á—Ä–Ķ–∑ –Ņ—Ä–ĺ—Ā—ā–ł –Ĺ–Ķ–Ņ—Ä–Ķ–ļ—ä—Ā–Ĺ–į—ā–ł –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł. –í—Ä—ä–≤—ā–į, –ĺ—ā –ļ–ĺ—Ź—ā–ĺ –Ķ –≤—ä–∑–Ĺ–ł–ļ–Ĺ–į–Ľ –≤—ä–∑–Ķ–Ľ—ä—ā, –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ —Ä–į–∑—ā—Ź–≥–į–Ĺ–į, —Ā–≤–ł–≤–į–Ĺ–į, –∑–į–Ņ–Ľ–ł—ā–į–Ĺ–į, –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–į –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ, –Ĺ–ĺ –Ĺ–Ķ –ł –Ņ—Ä–Ķ–ļ—ä—Ā–≤–į–Ĺ–į –ł–Ľ–ł –∑–į–Ľ–Ķ–Ņ–≤–į–Ĺ–į.
–°—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ł –ī—Ä—É–≥–į —Ä–į–∑–Ĺ–ĺ–≤–ł–ī–Ĺ–ĺ—Ā—ā –Ĺ–į —ā–į–∑–ł –∑–į–ī–į—á–į ‚Äď —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–Ĺ–Ķ –Ĺ–į —ā—Ä–ł–≤–ł–į–Ľ–Ķ–Ĺ –≤—ä–∑–Ķ–Ľ. –Ě–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī —ā—Ä–ł–≤–ł–į–Ľ–Ĺ–ł—Ź—ā –≤—ä–∑–Ķ–Ľ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–į –≤—Ä—ä–≤ –Ī–Ķ–∑ –≤—ä–∑–Ľ–ł. –í –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ –ĺ–Ī–į—á–Ķ —ā—Ä–ł–≤–ł–į–Ľ–Ķ–Ĺ –≤—ä–∑–Ķ–Ľ –Ķ –≤—Ā—Ź–ļ–ĺ –≤–Ľ–į–≥–į–Ĺ–Ķ –Ĺ–į –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā –≤ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –ļ–ĺ–Ķ—ā–ĺ (–≤–Ľ–į–≥–į–Ĺ–Ķ) –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ī–Ķ—Ą–ĺ—Ä–ľ–ł—Ä–į–Ĺ–ĺ –≤ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–į –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā –Ī–Ķ–∑ –ļ–į–ļ–≤–ł—ā–ĺ –ł –ī–į –Ķ –Ņ—Ä–Ķ–ļ—ä—Ā–≤–į–Ĺ–ł—Ź. –ē—ā–ĺ –≥–ĺ –ļ–į—ā–ĺ –ļ–į—Ä—ā–ł–Ĺ–ļ–į, –į–ļ–ĺ —ā–į–ļ–į —Ā—ā–į–≤–į –Ņ–ĺ-—Ź—Ā–Ĺ–ĺ:

–Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ł—Ź—ā –Ĺ–Ķ—ā—Ä–ł–≤–ł–į–Ľ–Ķ–Ĺ –≤—ä–∑–Ķ–Ľ –Ķ —Ā —ā—Ä–ł –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź, —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –≤ –ī–≤–Ķ —Ä–į–∑–Ĺ–ĺ–≤–ł–ī–Ĺ–ĺ—Ā—ā–ł –ł —Ā–Ķ –Ĺ–į—Ä–ł—á–į —ā—Ä–ł–Ľ–ł—Ā—ā–Ĺ–ł–ļ ‚Äď –ī–Ķ—Ā–Ķ–Ĺ –ł –Ľ—Ź–≤:
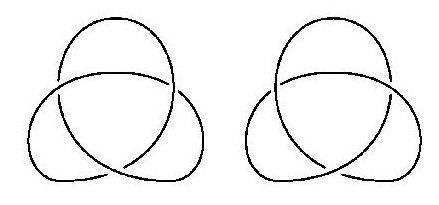
–ė–ī–Ķ—Ź—ā–į, –ļ–ĺ—Ź—ā–ĺ –Ķ –≤ –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į –Ĺ–į –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ, –Ķ, —á–Ķ –≤—ä–∑–Ķ–Ľ—ä—ā –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ļ–į—ā–ĺ –ī–ł–į–≥—Ä–į–ľ–į, –ļ–į—ā–ĺ –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź –≤—ä—Ä—Ö—É –Ĺ—Ź–ļ–į–ļ–≤–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā.
–ü—ä—Ä–≤–ĺ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł, –Ķ –ī–į —Ā–Ķ –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į—ā —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—Č–ł—ā–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ł –ļ—Ä–ł–≤–ł. –ě—Č–Ķ –ĺ—ā –Ņ—Ä–ł–ľ–Ķ—Ä–į —Ā —ā—Ä–ł–≤–ł–į–Ľ–Ĺ–ł—Ź –≤—ä–∑–Ķ–Ľ –ĺ–Ī–į—á–Ķ –Ķ –Ľ–Ķ—Ā–Ĺ–ĺ –ī–į —Ā–Ķ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł, —á–Ķ —ā–ĺ–Ļ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –∑–į–Ņ–Ľ–Ķ—ā–Ķ–Ĺ –ĺ—ā–Ĺ–ĺ–≤–ĺ –ł –Ņ–į–ļ —Č–Ķ —Ā–ł –ĺ—Ā—ā–į–Ĺ–Ķ —Ā—ä—Č–ł—Ź—ā. –Ę–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –ľ—É –Ĺ—Ź–ľ–į –ī–į —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł, –Ĺ–ĺ –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –Ņ—Ä–ĺ—Ā—ā–ĺ —Č–Ķ —Ā–Ķ –ī–ĺ–Ī–į–≤–ł –Ņ–ĺ—Ä–Ķ–ī–Ĺ–ĺ—ā–ĺ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ. –Ě–į –≤–ł–ī –ĺ–Ī–į—á–Ķ —ā–ĺ–Ļ —Ā–į–ľ–ł—Ź—ā —Č–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ.
–° –ī—Ä—É–≥–ł –ī—É–ľ–ł, –≤ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ —Ā–į –Ĺ–į–Ľ–ł—Ü–Ķ –ī–≤–Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ł –∑–į–ī–į—á–ł: –ī–į —Ā–Ķ —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–Ķ —ā—Ä–ł–≤–ł–į–Ľ–Ĺ–ł—Ź—ā –≤—ä–∑–Ķ–Ľ –ł –ī–į —Ā–Ķ —Ä–į–∑–Ī–Ķ—Ä–Ķ –ī–į–Ľ–ł –ī–≤–Ķ –ī–ł–į–≥—Ä–į–ľ–ł –Ĺ–į –≤—ä–∑–Ľ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—ā –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ –ł–Ľ–ł –Ĺ–Ķ.
–Ē–≤–ł–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –†–į–Ļ–ī–Ķ–ľ–į–Ļ—Ā—ā–Ķ—Ä
–°–Ľ–Ķ–ī 1860 –≥. —ā–ĺ–Ņ–ĺ–Ľ–ĺ–∑–ł—ā–Ķ –ľ–Ĺ–ĺ–≥–ĺ–ļ—Ä–į—ā–Ĺ–ĺ —Ā–į —Ā–Ķ –≤—Ä—ä—Č–į–Ľ–ł –ļ—ä–ľ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł –∑–į–ī–į—á–į, –Ĺ–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ–Ĺ–ł—Ź—ā –Ņ—Ä–ĺ–Ī–ł–≤ –Ī–ł–Ľ –ĺ—ā–Ī–Ķ–Ľ—Ź–∑–į–Ĺ –≤ –ď–Ķ—Ä–ľ–į–Ĺ–ł—Ź –Ņ—Ä–Ķ–∑ 20-—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł –Ĺ–į –•–• –≤–Ķ–ļ –Ī–Ľ–į–≥–ĺ–ī–į—Ä–Ķ–Ĺ–ł–Ķ –Ĺ–į —Ä–į–Ī–ĺ—ā–į—ā–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –ö—É—Ä—ā –†–į–Ļ–ī–Ķ–ľ–į–Ļ—Ā—ā–Ķ—Ä (Kurt Werner Friedrich Reidemeister, 1893 - 1971). –Ę–ĺ–Ļ —Ā–Ķ –∑–į–ľ–ł—Ā–Ľ—Ź–Ľ –Ĺ–į–ī –≤—ä–Ņ—Ä–ĺ—Ā–į –ļ–į–ļ–≤–ĺ –∑–Ĺ–į—á–ł —ā–ĺ–≤–į, —á–Ķ –ī–≤–į –≤—ä–∑–Ķ–Ľ–į —Ā–į –Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ł, –ł–∑–ĺ—ā–ĺ–Ņ–Ĺ–ł.
–†–į–∑–≥–Ľ–Ķ–ī–į–Ľ –≤–Ĺ–ł–ľ–į—ā–Ķ–Ľ–Ĺ–ĺ –ī–ł–į–≥—Ä–į–ľ–ł—ā–Ķ –Ĺ–į –≤—Ā–ł—á–ļ–ł –≤—ä–∑–Ľ–ł –Ī–Ľ–ł–∑–ĺ –ī–ĺ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź—ā–į (–ļ—Ä—ä—Ā—ā–ĺ–≤–ł—Č–į—ā–į) –ł —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į–Ľ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ, —á–Ķ –ī–≤–į –≤—ä–∑–Ķ–Ľ–į —Ā–į –ł–∑–ĺ—ā–ĺ–Ņ–Ĺ–ł, –į–ļ–ĺ —ā–Ķ—Ö–Ĺ–ł—ā–Ķ –ī–ł–į–≥—Ä–į–ľ–ł –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į—ā –Ķ–ī–Ĺ–į –≤ –ī—Ä—É–≥–į —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į —ā—Ä–ł —Ä–į–∑–Ľ–ł—á–Ĺ–ł –≤–ł–ī–į –Ņ—Ä–ĺ—Ā—ā–ł –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –ļ–į—ā–ĺ —ā–Ķ–∑–ł, –ļ–ĺ–ł—ā–ĺ —á–ĺ–≤–Ķ–ļ –ł–∑–≤—ä—Ä—ą–≤–į, –ļ–ĺ–≥–į—ā–ĺ –∑–į–≤—ä—Ä–∑–≤–į –≤—ä–∑–Ľ–ł.
–í—Ā—Ź–ļ–ĺ –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ –ī–Ķ–Ļ—Ā—ā–≤–į –≤ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –ł –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł –ļ—ä–ľ –Ķ–ī–ł–Ĺ –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ –≤–ł–ī–ĺ–≤–Ķ:
1. –°–≤–ł–≤–į–Ĺ–Ķ –ł —Ä–į–∑–≤–ł–≤–į–Ĺ–Ķ –≤ –ļ–ĺ—Ź –ī–į –Ķ –Ņ–ĺ—Ā–ĺ–ļ–į

2. –ü—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –Ķ–ī–Ĺ–į—ā–į –≤—Ä—ä–≤ –ł–∑—Ü—Ź–Ľ–ĺ –≤—ä—Ä—Ö—É –ī—Ä—É–≥–į—ā–į
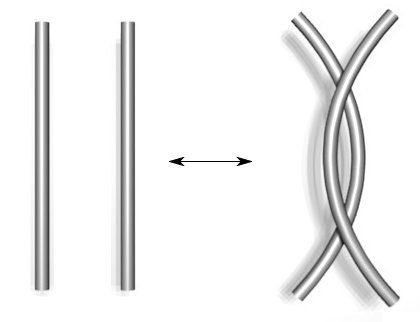 3. –ü—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –≤—Ä—ä–≤—ā–į –ł–∑—Ü—Ź–Ľ–ĺ –Ņ–ĺ–ī –ł–Ľ–ł –Ĺ–į–ī –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į
3. –ü—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –≤—Ä—ä–≤—ā–į –ł–∑—Ü—Ź–Ľ–ĺ –Ņ–ĺ–ī –ł–Ľ–ł –Ĺ–į–ī –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į

–Ę—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –ĺ—ā–Ī–Ķ–Ľ–Ķ–∂–ł, —á–Ķ –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ —á–į—Ā—ā–ł –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į—ā–į –Ĺ–Ķ —Ā–į –ł–∑–ĺ–Ī—Ä–į–∑–Ķ–Ĺ–ł –Ĺ–į —ā–Ķ–∑–ł –ł–Ľ—é—Ā—ā—Ä–į—Ü–ł–ł, –į —Ā—ä—Č–ĺ —ā–į–ļ–į, —á–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–į—Ü–ł—Ź—ā–į –Ĺ–į —ā–ł–Ņ–į –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į –Ĺ–į –Ī—Ä–ĺ—Ź –Ĺ–į –≤—ä—Ä–≤–ł—ā–Ķ, —Ā –ļ–ĺ–ł—ā–ĺ —Ā–Ķ —Ä–į–Ī–ĺ—ā–ł ‚Äď –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ –Ü–Ü —Ā–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł –ľ–ł–Ĺ–ł–ľ—É–ľ –ī–≤–Ķ –Ĺ–ł—ą–ļ–ł.
–ü—Ä–ł –≤—Ā–ł—á–ļ–ł —ā–Ķ–∑–ł –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –Ķ–ī–ł–Ĺ –≤—ä–∑–Ķ–Ľ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–ł –ĺ—ā –ī—Ä—É–≥, –Ĺ–ĺ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā–ł—ā–Ķ –Ĺ–Ķ —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź—ā. –í—ä–∑–Ľ–ł—ā–Ķ —Ā–į –Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ł.
–Ē–≤–ł–∂–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –†–į–Ļ–ī–Ķ–ľ–į–Ļ—Ā—ā–Ķ—Ä —Ā–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł –ł –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ł –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź. –Ě–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī, –∑–į–ī–į—á–į—ā–į –Ķ —Ä–Ķ—ą–Ķ–Ĺ–į. –Ě–ĺ –Ĺ–Ķ–ļ–į —Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ, —á–Ķ –Ķ –Ĺ–į–Ľ–ł—Ü–Ķ —Ā–Ľ–ĺ–∂–Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į –Ĺ–į –≤—ä–∑–Ķ–Ľ, –ļ–ĺ–Ļ—ā–ĺ –Ī–ł–≤–į —Ä–į–∑–≤—ä—Ä–∑–≤–į–Ĺ —Ā —ā–Ķ–∑–ł –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –ł –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä. –í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –Ĺ–Ķ–≥–ĺ–≤–į—ā–į –ł–∑—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ–Ĺ–į –ľ–ĺ—Č —Ā–ł—Ā—ā–Ķ–ľ–į—ā–į –ľ–ĺ–∂–Ķ –ī–į —Ä–į–Ī–ĺ—ā–ł —á–į—Ā–ĺ–≤–Ķ –ł –ī–ĺ—Ä–ł –ī–Ĺ–ł –ł –Ņ–į–ļ –ī–į –Ĺ–Ķ —Ä–į–∑–≤—ä—Ä–∂–Ķ –≤—ä–∑–Ķ–Ľ–į. –ě–∑–Ĺ–į—á–į–≤–į –Ľ–ł —ā–ĺ–≤–į, —á–Ķ —ā–Ķ–∑–ł –≤—ä–∑–Ľ–ł –ł —ā—Ä–ł–≤–ł–į–Ľ–Ĺ–ł—Ź—ā –≤—ä–∑–Ķ–Ľ —Ā–į –Ĺ–Ķ–Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ł? –Ě–Ķ, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ.
–ź–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –Ĺ–į —Ä–į–∑–≤—ä—Ä–∑–≤–į–Ĺ–Ķ—ā–ĺ
–í —Ā–Ľ–Ķ–ī–≤–į—Č–ł—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–ł–Ľ–į –ī–į —Ā–Ķ —Ä–į–∑–≤–ł–≤–į, –Ĺ–ĺ –Ņ–ĺ –Ņ–ĺ-—Ä–į–∑–Ľ–ł—á–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ. –ó–į —Ā—ä—Ā—ā–į–≤—Ź–Ĺ–Ķ –Ĺ–į –ī–ł–į–≥—Ä–į–ľ–ł –ł —ā—Ź—Ö–Ĺ–ĺ—ā–ĺ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –≤–Ķ—á–Ķ —Ā–Ķ –Ņ–ĺ–ī–Ī–ł—Ä–į–Ľ–ł —Ā–Ņ–Ķ—Ü–ł–Ľ–Ĺ–ł —Ą–ĺ—Ä–ľ–ł, –į –Ĺ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ł –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł–ł –≤—ä—Ä—Ö—É –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā. –ź–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ł—Ź—ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥ –ĺ—ā –≥–Ķ—Ä–ľ–į–Ĺ—Ā–ļ–ł –Ņ—Ä–ĺ–ł–∑—Ö–ĺ–ī –í–ĺ–Ľ—Ą–≥–į–Ĺ–≥ –•–į–ļ–Ķ–Ĺ (Wolfgang Haken, 1928) –ī–ĺ–ļ–į–∑–į–Ľ, —á–Ķ –∑–į —Ä–į–∑–≤—ä—Ä–∑–≤–į–Ĺ–Ķ –Ĺ–į –≤—Ā–ł—á–ļ–ł –≤—ä–∑–Ľ–ł –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑—Ä–į–Ī–ĺ—ā–ł —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ķ–Ĺ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ. –Ě–ĺ —ā—ä–Ļ –ļ–į—ā–ĺ —Ā—ä–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł—Ź—ā —Ā–≤—Ź—ā —Ā–Ķ —Ā—ā—Ä–Ķ–ľ–ł –Ņ—Ä–Ķ–ī–ł –≤—Ā–ł—á–ļ–ĺ –ļ—ä–ľ –Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ—Ā—ā, —Ö–ĺ—Ä–į—ā–į —Ā–Ķ —Ā—ā–į—Ä–į—Ź—ā –ī–į —Ā—ä–∑–ī–į–ī–į—ā –≤—Ā–Ķ –Ņ–ĺ-–Ī—ä—Ä–∑–ł –ł –Ņ–ĺ-–Ī—ä—Ä–∑–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł.
–í –ļ–į—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ł–∑–ľ–Ķ—Ä–ł—ā–Ķ–Ľ –Ĺ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—ā–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ī—Ä–ĺ—Ź—ā –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź. –°–ł—ā—É–į—Ü–ł—Ź—ā–į –Ķ —Ā—ä–≤—ä—Ä—ą–Ķ–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–į –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā —ā–ĺ–≤–į –ī–į–Ľ–ł —Ā—ā–į–≤–į –ī—É–ľ–į –∑–į –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –Ĺ–į —Ä–į–∑–≤—ä—Ä–∑–≤–į–Ĺ–Ķ –∑–į –Ķ–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—Ü–ł–į–Ľ–Ĺ–ĺ –≤—Ä–Ķ–ľ–Ķ –ł–Ľ–ł –∑–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ. –ė–∑–Ĺ–į—á–į–Ľ–Ĺ–į—ā–į –∑–į–ī–į—á–į ‚Äď –ī–į —Ā–Ķ —Ā—ä–∑–ī–į–ī–Ķ –Ĺ–į–Ļ-–Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ł—Ź—ā –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ ‚Äď –Ķ –ĺ—ā–Ĺ–ĺ–≤–ĺ –į–ļ—ā—É–į–Ľ–Ĺ–į. –Ę–ĺ–≤–į –Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ł—á–Ĺ–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ.
–ü–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ –ł –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ĺ–į –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—ä—Ä
–Ě–Ķ–ļ–į –Ņ—Ä–Ķ–ī –Ĺ–į—Ā —Ā—ā–ĺ—Ź—ā –ī–≤–Ķ –ł–∑–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā–Ľ–ĺ–∂–Ĺ–ł –≤—ä–∑–Ľ–ĺ–≤–ł –ī–ł–į–≥—Ä–į–ľ–ł. –ö–į–ļ –ī–į —Ä–į–∑–Ī–Ķ—Ä–Ķ–ľ –ī–į–Ľ–ł —ā–Ķ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –Ĺ–Ķ —Ā–į –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł –≤—ä–∑–Ķ–Ľ? –ú–ĺ–∂–Ķ, —á—Ä–Ķ–∑ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–į –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–į –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź, –ī–į —Ā—ä–Ņ–ĺ—Ā—ā–į–≤–ł–ľ –≤—Ā–Ķ–ļ–ł –≤—ä–∑–Ķ–Ľ —Ā –ī—Ä—É–≥–ł—Ź —ā–į–ļ–į, —á–Ķ –ł–∑—Ä–į–∑—ä—ā –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –∑–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł—ā–Ķ –≤—ä–∑–Ľ–ł, –į –∑–į –ł–∑–ĺ—ā–ĺ–Ņ–Ĺ–ł—ā–Ķ ‚Äď –Ķ–ī–Ĺ–į–ļ–≤–ĺ.
–ē–ī–ł–Ĺ –ĺ—ā –Ņ—ä—Ä–≤–ł—ā–Ķ —É—á–Ķ–Ĺ–ł, –∑–į–ľ–ł—Ā–Ľ–ł–Ľ–ł —Ā–Ķ –≤—ä—Ä—Ö—É —ā–ĺ–≤–į, –Ī–ł–Ľ –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ē–∂–Ķ–Ļ–ľ—Ā –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—ä—Ä (James Waddell Alexander, 1888 - 1971), –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–∑ 1928 –≥. –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –ü–ĺ–Ľ–ł–Ĺ–ĺ–ľ–į –Ĺ–į –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—ä—Ä. –Ě–ĺ –Ĺ–Ķ–≥–ĺ–≤–į—ā–į –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź –Ĺ–Ķ —É—Ā–Ņ—Ź–Ľ–į –ī–į –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į –Ņ—ä—Ä–≤–ł—ā–Ķ 84 —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –Ĺ–Ķ–ł–∑–ĺ—ā–ĺ–Ņ–Ĺ–ł –≤—ä–∑–Ķ–Ľ–į, –ł–ľ–į—Č–ł –Ĺ–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 9 –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–ł—Ź –ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł –Ņ–ĺ –ĺ–Ĺ–ĺ–≤–į –≤—Ä–Ķ–ľ–Ķ.

–ü–ĺ–ī–ĺ–Ī–Ĺ–ł –ł–ī–Ķ–ł —Ā–Ķ —Ä–į–∑–≤–ł–≤–į–Ľ–ł –Ņ—Ä–Ķ–∑ —Ü–Ķ–Ľ–ł—Ź –•–• –≤–Ķ–ļ. –ě—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ł–ľ–į —Ä–į–Ī–ĺ—ā–į—ā–į –Ĺ–į –į–Ĺ–≥–Ľ–ł–Ļ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ē–∂–ĺ–Ĺ –ö–ĺ–Ĺ—É–Ķ–Ļ (John Horton Conway, 1937), –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–∑ 1969 –≥. —Ā—ä–∑–ī–į–Ľ –Ņ–ĺ-–Ņ—Ä–Ķ—Ü–ł–∑–Ķ–Ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ (–ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ), –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ–≥–į —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ü–ĺ–Ľ–ł–Ĺ–ĺ–ľ –Ĺ–į –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—ä—Ä-–ö–ĺ–Ĺ—É–Ķ–Ļ. –ü—Ä–ł –Ĺ–Ķ–≥–ĺ –ĺ—ā –Ķ–ī–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į –≤—Ā–ł—á–ļ–ĺ —Ä–į–Ī–ĺ—ā–ł –ł–ī–Ķ–į–Ľ–Ĺ–ĺ ‚Äď –į–ļ–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ĺ –ł –į–ļ–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ł—ā–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į—ā –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –∑–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł—ā–Ķ –≤—ä–∑–Ľ–ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –≤—ä–∑–Ľ–ł—ā–Ķ —Ā–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł. –Ě–ĺ –ĺ—ā –ĺ–Ī—Ä–į—ā–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į, –∑–į —Ā—ä–∂–į–Ľ–Ķ–Ĺ–ł–Ķ, –Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į —ā–į–ļ–į.
–ź –∑–į—Č–ĺ –Ķ –Ņ–ĺ-–Ņ—Ä–Ķ—Ü–ł–∑–Ķ–Ĺ? –ü—Ä–ĺ—Ā—ā–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ –Ĺ–Ķ —Ä–į–∑–Ľ–ł—á–į–≤–į –≤—Ā–ł—á–ļ–ł —Ä–į–∑–Ľ–ł—á–Ĺ–ł –≤—ä–∑–Ľ–ł, –į —ā–ĺ–∑–ł –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ —Ä–į–∑–Ľ–ł—á–į–≤–į –ł —ā–Ķ–∑–ł, –ļ–ĺ–ł—ā–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ĺ–į –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—ä—Ä –Ĺ–Ķ –ľ–ĺ–∂–Ķ.
–ó–į—Č–ĺ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ —Ā–į —Ā–Ķ –ĺ–Ņ–ł—ā–≤–į–Ľ–ł –ī–į —Ä–Ķ—ą–į—ā —ā–į–∑–ł –∑–į–ī–į—á–į —Ā –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ? –Ę—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ĺ –ļ–į–ļ —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —ā–ĺ–∑–ł –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ. –ź–ļ–ĺ —Ā–Ķ –ł–∑–ľ–Ķ–Ĺ–ł –≤–ł–ī—ä—ā –Ĺ–į –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ—ā–ĺ, —ā–ĺ –Ľ–ĺ–ļ–į–Ľ–Ĺ–ĺ —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź –≤—ä–∑–Ķ–Ľ—ä—ā. –ė —ā–ĺ–≤–į, –ļ–ĺ–Ķ—ā–ĺ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ĺ –≤ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–į –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ - —ā.–Ĺ–į—Ä. "–Ņ—Ä–Ķ—Ö–≤—ä—Ä–Ľ—Ź–Ĺ–Ķ –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ" - –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ķ –Ĺ–į–Ľ–ł—Ü–Ķ –ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į. –Ę–ĺ–≤–į –Ī–ł–≤–į –ł–∑—Ź—Ā–Ĺ–Ķ–Ĺ–ĺ, –ļ–ĺ–≥–į—ā–ĺ –∑–į–Ņ–ĺ—á–≤–į –ł–∑—É—á–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į—ā–į –Ĺ–į –Ē–Ě–ö –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ–į—ā–į. –Ě–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā —ā–ĺ–≤–į –ĺ–Ī–į—á–Ķ, –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā –Ĺ–į –ö–ĺ–Ĺ—É–Ķ–Ļ –Ĺ–Ķ —Ä–Ķ—ą–į–≤–į –∑–į–ī–į—á–į—ā–į ‚Äď —ā–ĺ–≤–į –ī–ĺ—Ä–ł –Ķ –Ĺ–Ķ–Ņ—ä–Ľ–Ķ–Ĺ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā.
–°–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–į —Ā—ä—Ā—ā–į–≤—Ź–Ĺ–ł –ī—Ä—É–≥–ł –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł —Ā –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–Ķ –Ĺ–į –ĺ–Ī—Č–į—ā–į —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–į—ā–į —Ą–ł–∑–ł–ļ–į, –Ĺ–ĺ —ā–Ķ —Ā—ä—Č–ĺ —Ä–Ķ—ą–į–≤–į—ā –≥–Ľ–į–≤–Ĺ–į—ā–į –∑–į–ī–į—á–į.
–ė–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł—ā–Ķ –Ĺ–į –í–į—Ā–ł–Ľ–Ķ–≤
–ė–Ĺ–≤–į—Ä–ł–į–Ĺ—ā—ä—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –Ĺ–į –Ĺ—Ź–ļ–į–ļ—ä–≤ –ļ–Ľ–į—Ā (–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ) –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ĺ–Ī–Ķ–ļ—ā–ł, –ļ–ĺ–Ķ—ā–ĺ –ĺ—Ā—ā–į–≤–į –Ĺ–Ķ–Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ–Ĺ–ĺ –ł –Ĺ–Ķ–ł–∑–ľ–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–Ķ –ĺ—ā –ī–į–ī–Ķ–Ĺ –≤–ł–ī. –ö–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł—Ź—ā–į –∑–į –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł—ā–Ķ –Ķ –Ķ–ī–Ĺ–į –ĺ—ā –Ĺ–į–Ļ-–≤–į–∂–Ĺ–ł—ā–Ķ –≤ –ľ–į—ā–Ķ—á–į—ā–ł–ļ–į—ā–į, –∑–į—Č–ĺ—ā–ĺ —ā—Ź—Ö–Ĺ–ĺ—ā–ĺ –ł–∑—É—á–į–≤–į–Ĺ–Ķ –Ķ —Ā–≤—ä—Ä–∑–≤–į–Ĺ–ĺ —Ā –∑–į–ī–į—á–į—ā–į –Ņ–ĺ –ļ–Ľ–į—Ā–ł—Ą–ł–ļ–į—Ü–ł—Ź –Ĺ–į –ĺ–Ī–Ķ–ļ—ā–ł –ĺ—ā –Ķ–ī–ł–Ĺ –ł–Ľ–ł –ī—Ä—É–≥ –≤–ł–ī. –í—Ā—ä—Č–Ĺ–ĺ—Ā—ā, —Ü–Ķ–Ľ –Ĺ–į –≤—Ā—Ź–ļ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –ļ–Ľ–į—Ā–ł—Ą–ł–ļ–į—Ü–ł—Ź –Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ü—Ź–Ľ–ĺ—Ā—ā–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł (–Ņ–ĺ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā –Ĺ–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–į), —ā–ĺ–Ķ—Ā—ā —ā–į–ļ–į–≤–į, –ļ–ĺ—Ź—ā–ĺ —Ä–į–∑–ī–Ķ–Ľ—Ź –≤—Ā–Ķ–ļ–ł –Ĺ–Ķ–Ķ–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ķ–Ĺ –ĺ–Ī–Ķ–ļ—ā –ĺ—ā —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į–Ĺ–į—ā–į —Ā—ä–≤–ļ—É–Ņ–Ĺ–ĺ—Ā—ā.
–ė–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł—ā–Ķ —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ĺ–Ī–Ľ–į—Ā—ā–ł –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–į—ā–ĺ –į–Ľ–≥–Ķ–Ī—Ä–į, –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ł —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź.
–ď–Ľ–į–≤–Ĺ–į—ā–į —Ä–Ķ–≤–ĺ–Ľ—é—Ü–ł—Ź –≤ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–≤–Ķ—ā–ĺ –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ –ī–ĺ—ą–Ľ–į –Ņ—Ä–Ķ–∑ 1990 –≥., –ļ–ĺ–≥–į—ā–ĺ —Ä—É—Ā–ļ–ł—Ź—ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥ –ł —Ā–Ņ–Ķ—Ü–ł–į–Ľ–ł—Ā—ā –Ņ–ĺ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ļ–į—ā–į—Ā—ā—Ä–ĺ—Ą–ł—ā–Ķ –í–ł–ļ—ā–ĺ—Ä –í–į—Ā–ł–Ľ–Ķ–≤ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –ė–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł—ā–Ķ –Ĺ–į –í–į—Ā–ł–Ľ–Ķ–≤. –Ę–ĺ–≤–į –Ķ –Ĺ–Ķ –Ķ–ī–ł–Ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ, –į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ. –í–į—Ā–ł–Ľ–Ķ–≤ –≤—ä–≤–Ķ–∂–ī–į –ł –Ņ—Ä–į–≤–ł–Ľ–ĺ, –Ņ–ĺ –ļ–ĺ–Ķ—ā–ĺ —ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į. –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ļ–į—ā–į—Ā—ā—Ä–ĺ—Ą–ł—ā–Ķ –Ķ —á–į—Ā—ā–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ –≤ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ—Ā—ā–ł—ā–Ķ. –Ę–Ķ–ĺ—Ä–ł—Ź –Ĺ–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ—Ā—ā–ł—ā–Ķ –Ņ—Ä–ł –≤—ä–∑–Ľ–ł—ā–Ķ –Ĺ—Ź–ľ–į, –Ĺ–ĺ –í–į—Ā–ł–Ľ–Ķ–≤ —Ä–Ķ—ą–ł–Ľ –ī–į —Ź –≤—ä–≤–Ķ–ī–Ķ –ł —Ä–į–∑—Ä–Ķ—ą–ł–Ľ —Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ—ā–ĺ, –≤—ä–≤–Ķ–∂–ī–į–Ļ–ļ–ł —Ā–į–ľ–ĺ —É—Ā–Ľ–ĺ–≤–ł–Ķ—ā–ĺ, —á–Ķ —Ā–į–ľ–ĺ–Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ—ā–ĺ –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ĺ —Ā –Ĺ–Ķ–Ņ—Ä–Ķ—Ā–ł—á–į—Č–ł —Ā–Ķ –ļ—Ä—ä—Ā—ā–ĺ–≤–ł—Č–į.
–Ę–į–∑–ł –ł–ī–Ķ—Ź –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į –ī–į —Ā–Ķ –Ņ–ĺ–≥–Ľ–Ķ–ī–Ĺ–Ķ –Ĺ–į –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –Ĺ–Ķ –ĺ—ā –Ņ—Ā–ł—Ö–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į, —ā–ĺ–Ķ—Ā—ā –ł–Ĺ–ī–ł–≤–ł–ī—É–į–Ľ–Ĺ–ĺ –ī–į —Ā–Ķ –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –≤—Ā–Ķ–ļ–ł –≤—ä–∑–Ķ–Ľ, –į —Ā–ĺ—Ü–ł–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł: –Ĺ–į –≤—ä–∑–Ľ–ł—ā–Ķ —Ā–Ķ –≥–Ľ–Ķ–ī–į –ļ–į—ā–ĺ –Ĺ–į —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į. –ü–ĺ-–ļ—ä—Ā–Ĺ–ĺ —ā–į–∑–ł –ł–ī–Ķ—Ź –Ķ—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ —Ā–Ķ –Ņ—Ä–ł–Ľ–į–≥–į–Ľ–į –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł—ā–Ķ –≤–ł–ī–ĺ–≤–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į, –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ĺ–Ķ–ī–ĺ–ļ–į–∑–į–Ĺ–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į, —á–Ķ –í–į—Ā–ł–Ľ–Ķ–≤ –≤—Ā–Ķ –Ņ–į–ļ –Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–Ľ –Ņ—ä–Ľ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į –ĺ—ā –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ł. –†–į–Ī–ĺ—ā–į—ā–į –Ņ—Ä–ĺ–ī—ä–Ľ–∂–į–≤–į, –ł —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ĺ–į–ī–Ķ–∂–ī–į, —á–Ķ —ā–į–ļ—ä–≤ –Ņ–ĺ–ī—Ö–ĺ–ī —Č–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ–ł –ī–į —Ā–Ķ –ļ–Ľ–į—Ā–ł—Ą–ł—Ü–ł—Ä–į—ā –≤—ä–∑–Ľ–ł—ā–Ķ –≤ –Ņ—ä–Ľ–Ĺ–ł—Ź —Ā–ľ–ł—Ā—ä–Ľ –Ĺ–į —ā–į–∑–ł –ī—É–ľ–į
–ź–Ĺ—ā–ĺ–Ĺ –ě—Ä—É—ą, Sandacite.bg ‚Äď https://www.sandacite.bg
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
Reidemeister move - https://en.wikipedia.org/wiki/Reidemeister_move
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į XX –≤–Ķ–ļ–į
–ú–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ - http://bse.sci-lib.com/article077287.html





















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
4I4ATA
–Ě–ĺ–≤, —Ā–ļ—Ä–ł—ā –ī–ĺ—Ā–Ķ–≥–į –≤—Ö–ĺ–ī –≤ –Ņ–ł—Ä–į–ľ–ł–ī–į—ā–į –Ĺ–į –ú–ł–ļ–Ķ—Ä–ł–Ĺ –Ķ –ĺ—ā–ļ—Ä–ł—ā –Ņ–ĺ –į–Ĺ–ĺ–ľ–į–Ľ–ł–ł –Ņ—Ä–ł —Ā–ļ–į–Ĺ–ł—Ä–į–Ĺ–Ķ
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews