"Шапката на Айнщайн" възхити математиците. Сега формата разтърсва физиката.

През 2023 г. математиците съобщиха, че 13-странна плочка е първият известен "айнщайн"- игра на думи от немското „ein“ – един, „stein“ – камък (или плочка), но екипът я нарича просто „шапката“, защото им напомня на шапка. Това е една единствена форма, която може перфектно да покрие безкрайна равнина, без да се създава повтарящ се модел, т.е. не може да бъде подредена с транслационна симетрия, с други думи - образува непериодична мозайка.

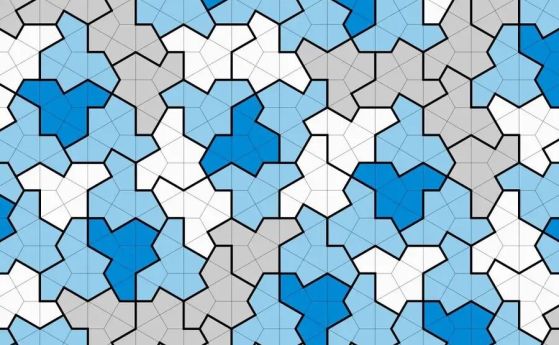Една единствена форма създава шарка, която никога не се повтаря. Кредит David Smith, Joseph Myers, Chaim Goodman-Strauss и Craig S. Kaplan

Сега са предсказани свойствата на двуизмерен материал, базиран на непериодичната мозайка с един елемент тип "шапка". Това е квазикристал, материал, който е подреден като кристал, но в който разположението на атомите не се повтаря. (Прочетете повече: "Квазикристалите - между два свята")

Интригуващо е, че този хипотетичен материал, базиран на тази непериодична мозайка, споделя свойства с графена, който е кристален материал, съобщават изследователите в статия, която ще се появи в Physical Review Letters.

"Той има много свойства, които свързваме с квазикристалите, но след това действа странно като кристал", разказва физикът Шинейд Грифин (Sinéad Griffin) от Националната лаборатория на Лорънс Бъркли в Калифорния, която не е участвала в изследването. "Това е наистина забавно проучване."

В тази анимация симулиран материал, базиран на плочката с шапка, показва улавяне на електрони при увеличаване на магнитното поле. (По-топлите цветове показват по-голяма вероятност да се намери електрон с нулева енергия на дадено място.) Електроните се улавят около плочките, които са огледални изображения на шапката. Кредит: A. Grushin/Institut Néel/CNRS

Преди това математиците се нуждаеха от повече от една форма, за да покрият безкрайна равнина по този неповтарящ се начин. Някои по-ранни неапериодични облицовки имат връзки с материали от реалния свят. Плочките на Пенроуз, базирани на комплекти от две плочки, открити през 70-те години на миналия век от математика Роджър Пенроуз, изглеждат като 2D срез през квазикристал. Такива квазикристали са открити в метеорити и отломки от тестове на атомни бомби, освен направените в лабораторията.

Учените, извършили проучването, са заинтригувани от идеята какъв може да бъде материалът, базиран на мозайка с "шапки". Физикът Адолфо Грушин (Adolfo Grushin) и колегите му изчисляват свойствата на електроните в 2D материал, в който атомите се намират на върховете на плочката.

За да определят характеристиките на материала, учените разглеждат връзката между енергиите на неговите електрони и техните дължини на вълните. (Според квантовата физика електроните преминават през материали като вълни; дължината на вълната означава размера на тези вълни.) В тази връзка енергия-дължина на вълната изследователите откриват поразителни прилики между квазикристала "шапка" и графена, който е 2D кристал от въглерод.

Това е така, защото много от върховете на плочките на шапката попадат по протежение на шестоъгълна решетка като тази на графена, обяснява Грушин, който е от Institut Néel на Националния център за научни изследвания (CNRS) в Гренобъл, Франция.

Фактът, че тази мозайка е съставена от една форма на плочка, а не от множество форми, също помага да се обясни как тя обхваща свойствата и на кристали, и на квазикристали. Фактът, че се използва една плочка, означава, че тя е по-близо до периодичните мозайки, отколкото други непериодични подреждания, без действително да се повтаря.

За разлика от графена обаче, 2D материалът на базата на непериодична мозайка от "шапки" е хирален, което означава, че електроните ще се държат различно, ако се обърне материала, сякаш се отразява в огледало. В реален материал това хирално свойство може да повлияе на това как светлината взаимодейства с веществото, например чрез завъртане на поляризацията на светлината, преориентирайки нейните електромагнитни вълни.

Още по-интересни характеристики се появяват, когато изследователите проучват какво би се случило, ако материалът бъде поставен в магнитно поле. В тази мозайка част от плочките са огледални изображения на останалите. Електроните, особено тези с нулева енергия, се улавят около обърнатите "шапки" при определени стойности на магнитното поле.

"Намерихме това за доста красиво“, коментира Грушин.

Въпреки че засега материалът е изцяло теоретичен, изследователите предлагат няколко начини, по които материалът може да бъде създаден. Например учените биха могли да поставят молекули върху повърхност една по една в модел, съответстващ на плочката "шапка". 

Справка: J. Schirmann et al. Physical properties of the aperiodic hat monotile: Graphenelike features, chirality, and zero modes. Physical Review Letters, in press, 2024.

Източник: A predicted quasicrystal is based on the ‘einstein’ tile known as the hat, Science News

Опити за обяснение за съществуването на квазикристали

Известно е, че при кристалите се наблюдава осева симетрия само от 1, 2, 3, 4 и 6-ти ред, съответно те съвпадат при завъртане на 180°, 120°, 90° и 60°. Няма кристални решетки със симетрия от 5-ти ред и над шести ред.

Но вече е признато съществуването и на квазикристали с пространствена решетка по законоверностите на мозайките на Пенроуз -  подредена, но никога не се повтаря. 

Да се обясни растежа и стабилността на квазикристалите е невъзможно със средствата на класическата кристалография. Липсва транслация, но как се обясняват белезите на все пак някаква подреденост?

Установено е, че съотношението на елементите на квазикристалите е в златна пропорция, което съчетано с петоъгълната симетрия натрапва приликата с "мозайките на Пенроуз" и както казва Питър Дж. Лу, от Харвардския университет като че ли ислямските математици и художници са открили схемата на квазикристалите преди стотици години.

Атомен модел на повърхността на квазикристал (Al-Pd-Mn).Снимка: wikipedia

Мозайка на нобеловия лауреат Пенроуз "двата ромба". Илюстрация: quadibloc.com

Фрагмент от средновековна ислямска мозайка, Исфахан, Иран. Снимка: math.ucr.edu

Въпреки, че непериодичните мозайки на Пенроуз са се появили като математическа игра, те са впрегнати да обяснят това ново явление. Тази теория приложил към кристалографията Алън Маккей. Той поставил атоми във възлите на мозайката на Пенроуз, изчислява картината на дифракция и получава модел със симетрия от десети ред, подобен на квазикристалните.

Фрагменти на атомната структура на квазикристалите могат да бъдат тримерни аналози на мозайките на Пенроуз - остри и тъпи ромбоедри с ъгли при върховете 63,43° и 116,57°, из които може да се сглоби многостен, наречен триаконтаедър със симетрия 53m.

В обемния си вариант мозайката на Пенроуз може да е съставена от икосаедри - дванайсетостени с триъгълни стени, като на всеки връх се срещат пет триъгълници, от където идва и симетрията от 5-ти порядък.

Проекция от 6-тото измерение

Преди да продължим, ви препоръчвам да прегледате раздел Четвъртото измерение в този сайт, ако досега не сте се сблъсквали с идеята за пространства с размерност над обичайната ни.

Тъй като да се опишат квазикристалите в 3D пространството не е толкова лесно, колкото при нормални кристални структури, на помощ ни идват и по-висшите пространства.

За да се определят нормалните кристали са достатъчни три цели числа (индекси на Милер), отразяващи триизмерната транслационна периодичност на структурата.

Необходимостта от n вектора съответства на nD-мерно пространство. С други думи, в пространство с по-висока размерност от трета, квазикристалите може да се опишат периодично.

Ще си обясним това с пример от една по-ниска размерност. Представете си една двумерна периодична решетка Да прекараме ос и проектираме върху нея точките, които попадат в ивицата около оста. Ако наклонът й някаква част от периода, да речем 1/2, то проекциите ще отразяват периодичната структура на двумерната решетка.

 

Но ако наклонът е някакво ирационално число като π (3.1415...) или златното сечение φ=1.618... - често срещано при кристалите, тогава проекциите ще са една непериодична едномерна решетка. Последователността на тези стойности изглежда повече или по-малко хаотична - липсва транслационна симетрия, ако не разширим пространството до две измерения, тогава всичко става ясно: нашият едномерен квазикристал е само част от проекцията на една периодична квадратна мрежа.

И така, за да се зададат целочислени индекси на квазикристалите са необходими най-малко 5 линейно независими вектори за многоъгълните квазикристали и 6 за икосаедрични квазикристали.

Тоест необходимо е пет- или шестмерно пространство, в което квазикристалите са периодични. При проекция в тримерното пространство периодичността изчезва и се превръща в необичайната петоъгълно-симетрична дифракционна картина.

Истинската квазипериодична структура в 3D-физическото пространство може да бъде получена чрез подходящи техники за проекция и сечение. Така че е достатъчно да се определи една единична клетка с nD-структура, чието съдържание се състои от "хиператоми", по аналогия на атомите в една нормална единична клетка в кристалите. Това ни позволява да се опише цялата структура на квазикристалите с ограничен набор от параметри.

Оказва се, че картината на мозайката на Пенроуз при квазикристалите се получава като сечение на пет- и шестмерна кубична решетка с наклонена равнина.

Не всички приемат това толкова сложно обяснение - то обяснява дифракционната картина, но не дава отговор на въпроса как локалните междуатомни взаимодействия може да стабилизират квазикристала и установят периодичност на далечни разстояния в едно хиперпространство.

В същото време, при растежа на кристала от стопилката, атомите се присъединяват към повърхността на зародиша по някакъв закон, който има локален характер. Как атомите "знаят" (заради естеството на междуатомните си взаимодействия) какви местната конфигурации може да образуват и какви не може за да се формира в двумерния случай мозайка на Пенроуз.

Някои смятат, че квазикристалът е всъщност микрокристално състояние, при което веществото се групира в икосаедрични клъстери, произволно свързани помежду си, а кристалографски ограничения върху такива опаковки няма, защото клъстерът може да има каквато и да е форма - той няма нужда да запълва с решетката си безкрайни пространства. Въпросът остава открит.

Още по темата

03/10/2023

Физика

Физици постигат свръхпроводимост и още нещо от квазикристали

05/06/2023

Математика

Плочка "вампирски айнщайн" надминава последното постижение на математиците

27/03/2023

Математика

Пробив в геометрията: Непериодична мозайка с еднакви плочки (видео)

19/05/2021

Физика

В първия тест за ядрена бомба е изкован „невъзможен“ квазикристал (видео)