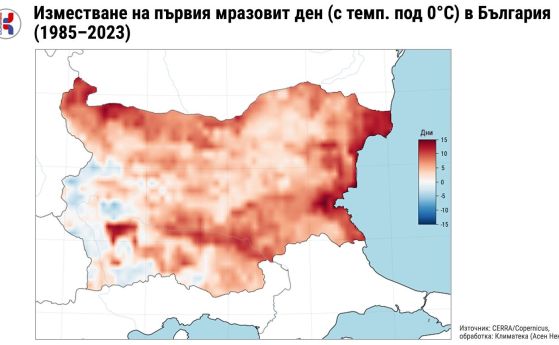

Двама млади компютърни специалисти - Саймън Макензи (Simon Mackenzie) и Харис Азиз (Haris Aziz) - може би са намерили начин да разделят торта за произволен брой хора като същевременно да е справедливo за всички участници, проблем, който учените се опитват да се справят най-малко от половин век.
Констатациите са интересни, защото много учени смятаха, че справедливото разделяне в тази ситуация е невъзможно, съобщава Ерика Кларайх (Erica Klarreich) от Quanta Magazine.
"Не може ли просто да изядат проклетото парче торта?" - пита ZME Science.
"Как да се раздели торта справедливо" е главоблъсканица, която много от нас се изправят най-малко веднъж в живота си. Например, двама може да искат парче от едно и също място, някои искат с цели плодове или ванилова глазура. Нещата стават все по-сложни с увеличаване на броя на хората. В края на краищата, всеки може да направи компромис, но за чистата математика няма такъв вариант. Трябва да има начин да се раздели една торта в еднакво справедливи парчета, така че всички участници да са доволни.
Това дори не е нов проблем. Например, Библията предлага решение. В книгата Битие, Авраам и Лот спорят как да си разделят парче земя. Авраам разделя земята на две части, които той оценява като равностойни, и след това предлага на Лот да избере това, което предпочита. По този начин, без значение какво е избрал Лот, Авраам е удовлетворен.
Нещата стават объркани, когато се дели тортата на три или четири парчета. Един забележителен алгоритъм, с който може да се раздели торта та на три е предложен от математиците Джон Селфридж (John Selfridge) и Джон Конуей (John Conway), който самостоятелно стига до същото решение през 60-те.
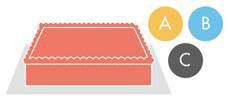 Алис, Боб и Чарли искат всеки да получи справедлив дял от една торта. Алис, Боб и Чарли искат всеки да получи справедлив дял от една торта. |
 Чарли разделя тортата на три парчета, които са еднакво ценни от неговата гледна точка. Чарли разделя тортата на три парчета, които са еднакво ценни от неговата гледна точка. |
 След това Алис и Боб трябва да си изберат парчета. В най-добрия случай, че Алис ще си избере едното парче, а Боб - друго парче и справедливото поделяне ще завърши успешно, защото Чарли ще получи това, което е останало, което вече е определил като еднакво удовлетворяващо. Но Алис и Боб избират едно и също парче. След това Алис и Боб трябва да си изберат парчета. В най-добрия случай, че Алис ще си избере едното парче, а Боб - друго парче и справедливото поделяне ще завърши успешно, защото Чарли ще получи това, което е останало, което вече е определил като еднакво удовлетворяващо. Но Алис и Боб избират едно и също парче. |
 Ако Алис и Боб изберат едно и също парче от тортата, тогава единият от тях (в случая Боб) да отрежете от едното толкова, колкото, според него, ще го направи равностойно на другото. Ако Алис и Боб изберат едно и също парче от тортата, тогава единият от тях (в случая Боб) да отрежете от едното толкова, колкото, според него, ще го направи равностойно на другото. |
|
Това е справедливо:
|
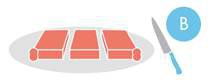 За да си поделят отрязаното малко парче, първо Боб го нарязва на три части, които са равностойни от неговата гледна точка. За да си поделят отрязаното малко парче, първо Боб го нарязва на три части, които са равностойни от неговата гледна точка. |
|
Това е справедливо:
|
Може да си помислите, че всичко започва отначало с малкото парченце, ако Алис и Чарли изберат един и същи дял от малкото парченце, което ще трябва да се дели по първото правило. Този процес предполага безкраен цикъл, така че това не е добро решение. Интересно е, че Чарли е винаги доволен, защото дори и ако един от другите играчи получава обрязано парче и да си разпределят останалата част от тортата, те все пак няма да вземат повече от цялото парче от тортата, която Чарли вече има, той е в един вид винаги печеливша ситуация, което означава, че "доминира" в играта за разпределянето на тортата. Чарли печели във всички сценарии.
Да си доминиращ играч означава, че трябва да си доволен, без значение какво парче си получил, което значително намалява сложността на проблема.
Този вид алгоритъм осигурява справедливо разделяне, но е безкрайно, и въпреки всякакви интересни предложения за подобрение, досега нямаше работно решение - не, докато Саймън Макензи, постдокторант изследовател от Карнеги Мелон и Харис Азиз, компютърен учен от Университета на Нов Южен Уелс, публикуват основополагащата си работа.
Алгоритъмът на двамата математици се основава на метода на Селфридж и Конуей. Подобно на други алгоритми преди това, протоколът предлага на някой да разреже тортата на n еднакво удовлетворяващи го парчета, след това - останалите играчи, за да коригират парчетата и да изберат своите фаворити. Различното е, че във фонов режим, протоколът се променя динамиката на играта и увеличава броя на доминиращите отношения между участниците.
Доминиращ играч означава, че ще бъде удовлетворен, без значение какво получи, така че сложността на проблема значително се намалява. Това не означава, че става по-лесно. Разделянето на тортата на n играчи може да изисква nnnnnn (n^n^n^n^n^n) стъпки и приблизително толкова корекции. За шепа играчи това означава, че са необходими повече повторения , отколкото са атомите във Вселената - "всичко за задоволяване на едно извратено обсесивно-компулсивно разстройство. Представете си, че такава порода хора са на вашия рожден ден. Тортата ще се скапе," - както се изразява иронично ZME Science.
Проблемът е най-малкото ограничен засега. Азис и Макензи казват, че вече имат идеи, как да направят своя алгоритъм по-прост и да намалят броя на стъпките.
Азис и Макензи ще представят своята работа на 10 октомври на 57-ия годишен симпозиум IEEE по Основи на компютърните науки.


 Отрязаното малко парченце се заделя за по-късно, а тримата избират в следния ред: първа е Алис, Боб - втори и Чарли е последен.
Отрязаното малко парченце се заделя за по-късно, а тримата избират в следния ред: първа е Алис, Боб - втори и Чарли е последен.  Сега изборът е в следния ред: първа е Алис, Чарли - втори и Боб е последен.
Сега изборът е в следния ред: първа е Алис, Чарли - втори и Боб е последен. 




















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон