Амебата има компютърни способности, превъзхождащи съвременните алгоритми (видео)

Изследователи демонстрираха, че амебата - едноклетъчен организъм с променлива форма на тялото от протоплазма - има уникални компютърни способности, които един ден могат да са конкурентна алтернатива на използваните от конвенционалните компютри методи, съобщава Phys.org.

Изследването е публикувано в Royal Society Open Science.

Изследователи, водени от Масаши Аоно (Masashi Aono) от Университета Кейо, възложиха на амеба, която да реши "проблема на търговския пътник" (TSP). TSP е задача за оптимизация, при която целта е да се намери най-краткият маршрут между няколко града, така че всеки град да бъде посетен само веднъж и началните и крайните точки да съвпадат.

Проблемът е NP-труден (повече в "Ако P = NP, човек ще бъде Бог"), което означава, че с увеличаването на броя на градовете времето, необходимо за решаването на задачата от компютър, нараства експоненциално. Сложността се дължи на големия брой възможни решения. Например за четири града има само три възможни маршрута. Но за осем града броят на възможните маршрути се увеличава до 2520. С други думи, става експоненциално по-трудно - и ще е нужно много повече време за компютрите да изберат най-добрия маршрут.

Впечатляващ обаче е фактът, че когато проблемът се усложнява, амебите го решават по напълно различен и по-ефективен начин от повечето алгоритми.

"В това изследване показахме, че времето, необходимо на амебата да намери разумно висококачествено решение за TSP, нараства линейно като размерът на проблема се увеличава от четири на осем", пишат изследователите в Royal Society Open Science. 

"Тези резултати могат да доведат до разработването на нови аналогови компютри, позволяващи приблизителни решения на сложни проблеми с оптимизация в линейно време".

Или по-просто - нашите най-съвременни електронни устройства наистина могат да научат нещо от амебата, а тя никак не е по-бърза от компютрите (вижте колко бавно се движи във видеото по-долу).

Проблемът става по-сложен експоненциално, а времето за обработката му за амебата се увеличава само линейно. Може да видите разликата:

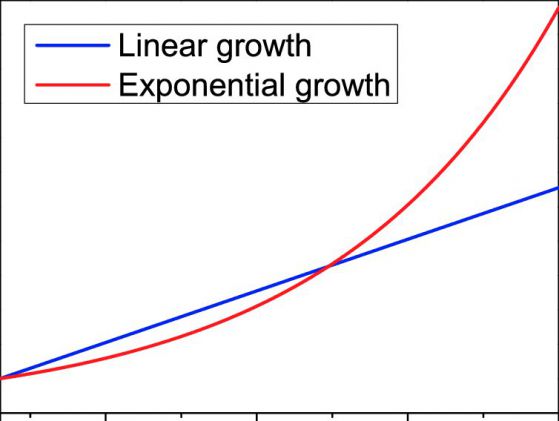_{Принципната разлика между линейно и експоненциално нарастване (Luo, Researchgate)}

Как работи

Учените използват определен вид амеба, плазмодий или Physarum polycephalum. Тази амеба непрекъснато деформира аморфното си тяло, като се придвижва псевдоподи (лъжливи крачка) със скорост около 1 мм/сек. 

Разбира се, амебите не знаят какво е град (доколкото знаем), така че в тази версия на TSP "градовете" са 64 тесни канали (осем "града", всеки от които съдържат осем канала), излизащи от кръгла плоча, поставена на горната част на лабораторен съд с хранителна среда с агар-агар.

За да получи достъп до агара и ефективно да абсорбира хранителните вещества, амебата навлиза в каналите.

Пътят на търговския пътник е нейната постоянно променяща се форма на тялото. Така тя формира едно тяло, когато влиза в един канал, друга форма на тялото, когато влезе втори канал и т.н.

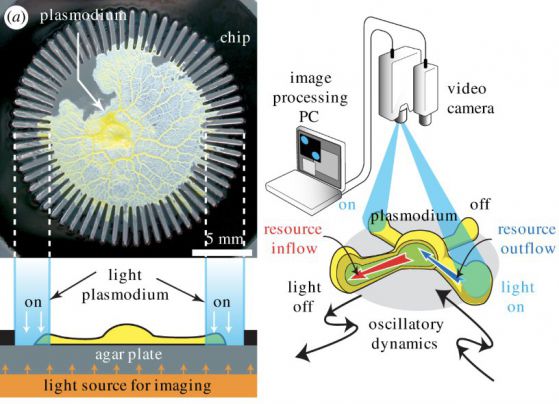_{Кредит: Aono et al., ©2018 Royal Society Open Science}

За да се увеличи максимално абсорбцията на хранителни вещества, амебата се опитва да се разшири вътре в плочата, за да влезе в контакт с колкото е възможно повече агар-агар. 

За да са сигурни, че амебата е влязла оптимално в "градовете", изследователите използват светлина (която не се харесва на амебата) за осветяване на някои канали, които са твърде отдалечени или вече са посетени, или за да я спрат да влезе в няколко канала едновременно.

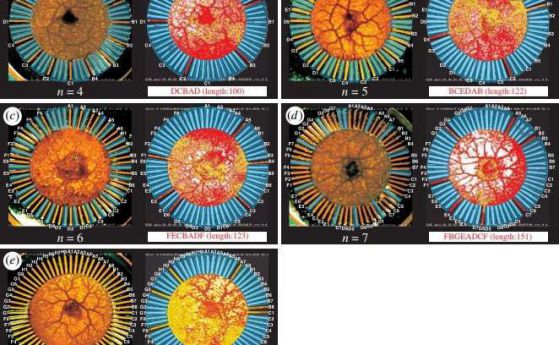
Така изследователите моделират задачата TSP. Например, в случая с четири града, обозначени от A до D, ако амебата заема канали A4, B2, C1 и D3, тогава съответното решение за TSP е C, B, D, A, C.

_{Кредит: Aono et al., ©2018 Royal Society Open Science}

В проучването екипът установи, че една амеба може да намери разумни (почти оптимални) решения за TSP в период от време, който расте само линейно като броят на градовете се увеличава от четири на осем. Конвенционалните компютри също могат да намерят приблизителни решения в линейно време, но подходът на амебата е напълно различен от традиционните алгоритми. Както обясняват учените, амебата изследва пространството на разтвора чрез постоянно преразпределяне на гела в аморфното си тяло при постоянна скорост, както и чрез обработка на оптична обратна връзка паралелно, вместо последователно.

"Интересното е, добавя екипът, че качеството на решението не се разваля, въпреки експоненциалното разширяване на пространството за търсене."

Изследователите обясняват, че ограничават експеримента само до осем канала, защото не могат да направят достатъчно голям и сложен съд за амебата, за да я тестват с повече "градове" , но смятат, че естественото желание на амебата да търси стабилно равновесие ще се справи със стотици "градове".

Въпреки че конвенционалният компютър все още може да разреши TSP много по-бързо от амебата, особено за малки размери, новите резултати са интригуващи и могат да доведат до разработването на нови аналогови компютри, които извличат приблизителни решения на изчислително сложни проблеми с много по-големи размери за линейно време.

Изследователите разработиха и компютърна симулация, наречена AmoebaTSP, която имитира някои от основните характеристики на начина, по който амебата се справя с проблема, включително непрекъснатото движение на гела, който с постоянна скорост навлиза и се изтегля от различни канали.

"Но все пак механизмът, чрез който амебата поддържа качеството на приблизителното решение, тоест най-късата дължина на маршрута, остава загадка. Изглежда, че свързаните в пространството и времето движения на разклоненията на амебата, разположени на далечни канали са ключови. Групите от разклонения изпълняват синхронизация и десинхронизация за споделяне на информацията, въпреки че са пространствено отдалечени."

В бъдеще изследователите планират да подобрят компютърните възможности с помощта на това, което научат от амебата.

"Ще проучим по-подробно как тази сложна пространствено-скоростна осцилаторна динамика повишава изчислителната производителност при намирането на решения с по-високо качество за по-кратко време", коментира съавторът Сонг-Ю Ким (Song-Ju Kim) от Университета Кейо.

_{Кредит: Aono et al., ©2018 Royal Society Open Science}

Проблемът NP=P

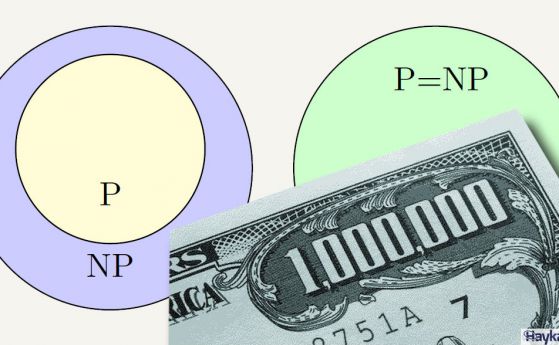
За хората, които мразят математиката и се плашат от сложни уравнения, изразът NP=P е измамно прост. Но върху доказателството му или за доказването на обратното (NP ≠ P) са работили безуспешно десетки години най-добрите умове на нашата планета. Това е една от седемте задачи на хилядолетието, за чието решаване математическият институт Клей дава един милион долара.

Нещо повече, ако някой успее обосновано и категорично да даде отговор, че NP и P са равни, това ще премахне всякакви ограничения пред човешкия ум и би отворило невероятни възможности пред нашата цивилизация. 

Просто казано, P са всички относително лесни задачи и NP е набор, който включва изглеждащи много, много трудни задачи, така че ако P = NP, това би означавало, че очевидно сложни проблеми всъщност имат сравнително лесни решения.

Въпросът се свежда до: задължително ли е по-лесно да се провери една задача, отколкото да се реши.

Още...

Още по темата

18/09/2017

Математика

Ако P = NP, човек ще бъде Бог