

–Р–ї–≥–Њ—А–Є—В—К–Љ, –њ—А–µ–і–љ–∞–Ј–љ–∞—З–µ–љ –і–∞ –љ–∞–Љ–µ—А–Є –љ–∞–є-–µ—Д–µ–Ї—В–Є–≤–љ–Є—П –њ—К—В –Њ—В –∞—В–Њ–Љ –і–Њ –∞—В–Њ–Љ –≤¬†–Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї, —Б–µ –Њ–Ї–∞–Ј–≤–∞, —З–µ —Б—К–Ј–і–∞–≤–∞ –љ–µ–≤–µ—А–Њ—П—В–љ–Њ —Б–ї–Њ–ґ–љ–Є –ї–∞–±–Є—А–Є–љ—В–Є. –Ю—Б–≤–µ–љ —З–µ –њ—А–∞–≤–Є –ї–∞–±–Є—А–Є–љ—В–Є, —В–µ—Е–љ–Є–Ї–∞—В–∞ –Љ–Њ–ґ–µ –і–∞ –њ–Њ–Љ–Њ–≥–љ–µ –Ј–∞ —Г—Б–Ї–Њ—А—П–≤–∞–љ–µ –љ–∞ –љ—П–Ї–Њ–Є –Є–љ–і—Г—Б—В—А–Є–∞–ї–љ–Є —Е–Є–Љ–Є—З–љ–Є —А–µ–∞–Ї—Ж–Є–Є.
–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ —Б–µ –љ–∞—А–Є—З–∞—В —В–∞–Ї–∞, –Ј–∞—Й–Њ—В–Њ¬†–њ–Њ–Ї–∞–Ј–≤–∞—В –њ–Њ-—Б–ї–Њ–ґ–љ–Є –Є –љ–µ–њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Є —Д–Њ—А–Љ–Є –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Ї–∞—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—В–∞ –Ї–Њ–љ—Ж–µ–њ—Ж–Є—П, –љ–∞—А–µ—З–µ–љ–∞ –љ–µ–њ–µ—А–Є–Њ–і–Є—З–љ–∞ –Љ–Њ–Ј–∞–є–Ї–∞,¬†–Ј–∞ —А–∞–Ј–ї–Є–Ї–∞ –Њ—В –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Є—В–µ –Ї—А–Є—Б—В–∞–ї–Є, —З–Є–Є—В–Њ –∞—В–Њ–Љ–Є —Б–∞ –њ–Њ–і—А–µ–і–µ–љ–Є –≤ –њ–Њ–≤—В–∞—А—П—Й–Є —Б–µ —Д–Њ—А–Љ–Є —Б —В—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ —Б–µ —Б–Є–љ—В–µ–Ј–Є—А–∞—В –≤ –ї–∞–±–Њ—А–∞—В–Њ—А–љ–Є —Г—Б–ї–Њ–≤–Є—П, —Б–∞ –Њ—В–Ї—А–Є—В–Є –Є —Б–ї–µ–і –њ—К—А–≤–∞—В–∞ –і–µ—В–Њ–љ–∞—Ж–Є—П –љ–∞ —П–і—А–µ–љ–Њ –Њ—А—К–ґ–Є–µ –њ—А–µ–Ј 1945 –≥.¬†–Є –≤ –Љ–µ—В–µ–Њ—А–Є—В–Є.
"–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ –Є–Љ–∞—В —Б–Є–Љ–µ—В—А–Є–Є, –Ї–Њ–Є—В–Њ –љ–µ –±–Є—Е–∞ –Љ–Њ–≥–ї–Є –і–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞—В –≤ [–љ–Њ—А–Љ–∞–ї–љ–Є—В–µ] –Ї—А–Є—Б—В–∞–ї–Є, –Ї–Њ–µ—В–Њ –µ –љ–µ—Й–Њ –Њ—З–∞—А–Њ–≤–∞—В–µ–ї–љ–Њ", —А–∞–Ј–Ї–∞–Ј–≤–∞ –§–µ–ї–Є–Ї—Б –§–ї–Є–Ї–µ—А (Felix Flicker) –Њ—В —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ –≤ –С—А–Є—Б—В–Њ–ї, –Т–µ–ї–Є–Ї–Њ–±—А–Є—В–∞–љ–Є—П. "–Ґ–Њ–≤–∞ –µ —В–∞–Ј–Є –Љ–љ–Њ–≥–Њ –Ї—А–∞—Б–Є–≤–∞ –Њ–±–ї–∞—Б—В –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞, –љ–Њ –≤ –Ї–Њ—П—В–Њ —Е–Њ—А–∞—В–∞ –Љ–Њ–≥–∞—В –і–∞ –Њ—Ж–µ–љ—П—В –Ї—А–∞—Б–Њ—В–∞—В–∞ –є –њ—А—П–Ї–Њ, –±–µ–Ј –љ–µ–њ—А–µ–Љ–µ–љ–љ–Њ –і–∞ –µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –і–∞ –Ј–љ–∞—П—В –њ–Њ–і—А–Њ–±–љ–Њ—Б—В–Є—В–µ."
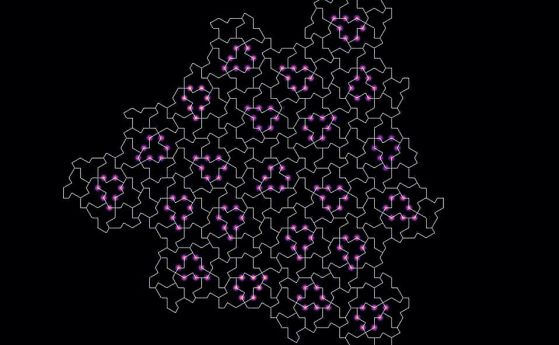
–Ш–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є –љ–∞–±–Њ—А –Њ—В –і–≤—Г–Є–Ј–Љ–µ—А–љ–Є –њ–Њ–і–ї–Њ–ґ–Ї–Є –љ–∞ –љ–µ–њ–µ—А–Є–Њ–і–Є—З–љ–∞ –Љ–Њ–Ј–∞–є–Ї–∞, –Є–Ј—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є—В–µ¬†–≥–µ–љ–µ—А–Є—А–∞—В –•–∞–Љ–Є–ї—В–Њ–љ–Њ–≤–Є —Ж–Є–Ї–ї–Є, –Ї–Њ–Є—В–Њ —Б–њ–Њ—А–µ–і —В—П—Е –Њ–њ–Є—Б–≤–∞—В –∞—В–Њ–Љ–љ–Є—П –Љ–Њ–і–µ–ї –љ–∞ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї.
 –Э–µ–њ–µ—А–Є–Њ–і–Є—З–љ–∞—В–∞ –Љ–Њ–Ј–∞–є–Ї–∞ –љ–∞ Ammann-Beenker —Б –њ–Њ-–і–µ–±–µ–ї–∞ —З–µ—А–љ–∞ –ї–Є–љ–Є—П, –њ—А–Њ—Б–ї–µ–і—П–≤–∞—Й–∞ –•–∞–Љ–Є–ї—В–Њ–љ–Њ–≤–∞—В–∞ —В—А–∞–µ–Ї—В–Њ—А–Є—П —З—А–µ–Ј –њ–Њ—Б–µ—Й–µ–љ–Є–µ –љ–∞ –≤—Б–µ–Ї–Є –≤—А—К—Е. –Ы–Є–ї–∞–≤–Є—В–µ –ї–Є–љ–Є–Є –љ–µ —Б–∞ —З–∞—Б—В –Њ—В –Њ–±–ї–Є—Ж–Њ–≤–Ї–∞—В–∞. –Ъ—А–µ–і–Є—В: Singh et al., Phys. Rev. X , 2024
–Э–µ–њ–µ—А–Є–Њ–і–Є—З–љ–∞—В–∞ –Љ–Њ–Ј–∞–є–Ї–∞ –љ–∞ Ammann-Beenker —Б –њ–Њ-–і–µ–±–µ–ї–∞ —З–µ—А–љ–∞ –ї–Є–љ–Є—П, –њ—А–Њ—Б–ї–µ–і—П–≤–∞—Й–∞ –•–∞–Љ–Є–ї—В–Њ–љ–Њ–≤–∞—В–∞ —В—А–∞–µ–Ї—В–Њ—А–Є—П —З—А–µ–Ј –њ–Њ—Б–µ—Й–µ–љ–Є–µ –љ–∞ –≤—Б–µ–Ї–Є –≤—А—К—Е. –Ы–Є–ї–∞–≤–Є—В–µ –ї–Є–љ–Є–Є –љ–µ —Б–∞ —З–∞—Б—В –Њ—В –Њ–±–ї–Є—Ж–Њ–≤–Ї–∞—В–∞. –Ъ—А–µ–і–Є—В: Singh et al., Phys. Rev. X , 2024
–§–ї–Є–Ї–µ—А –Є –Ї–Њ–ї–µ–≥–Є—В–µ –Љ—Г —Б–∞ —А–∞–Ј—А–∞–±–Њ—В–Є–ї–Є –∞–ї–≥–Њ—А–Є—В—К–Љ –Ј–∞ –±—К—А–Ј–Њ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ –Љ–∞—А—И—А—Г—В, –Ї–Њ–є—В–Њ –і–Њ–Ї–Њ—Б–≤–∞ –≤—Б–µ–Ї–Є –∞—В–Њ–Љ –≤ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї –≤–µ–і–љ—К–ґ –Є —Б–∞–Љ–Њ –≤–µ–і–љ—К–ґ. –Ф–Є–∞–≥—А–∞–Љ–Є—В–µ –љ–∞ —В–µ–Ј–Є –Љ–∞—А—И—А—Г—В–Є –Њ–±—А–∞–Ј—Г–≤–∞—В –Ї—А–∞—Б–Є–≤–Є –ї–∞–±–Є—А–Є–љ—В–љ–Є —Б—В—А—Г–Ї—В—Г—А–Є.
–Ю—В –µ–і–љ–∞ —Б—В—А–∞–љ–∞, –љ–∞–Љ–Є—А–∞–љ–µ—В–Њ –љ–∞ –•–∞–Љ–Є–ї—В–Њ–љ–Њ–≤–Є —Ж–Є–Ї–ї–Є –µ –Є–Ј–Ї–ї—О—З–Є—В–µ–ї–љ–Њ —В—А—Г–і–љ–Њ.
–†–µ—И–µ–љ–Є–µ—В–Њ –Є–Љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –і–∞ —А–µ—И–Є –Љ–љ–Њ–≥–Њ –і—А—Г–≥–Є —В—А—Г–і–љ–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –њ—А–Њ–±–ї–µ–Љ–Є, –Њ—В —Б–ї–Њ–ґ–љ–Є —Б–Є—Б—В–µ–Љ–Є –Ј–∞ –љ–∞–Љ–Є—А–∞–љ–µ –љ–∞ –Љ–∞—А—И—А—Г—В –і–Њ —Б–≥—К–≤–∞–љ–µ –љ–∞ –њ—А–Њ—В–µ–Є–љ–Є.
–°—К–Ј–і–∞–≤–∞–љ–µ—В–Њ –љ–∞ —В–∞–Ї—К–≤ –Љ–∞—А—И—А—Г—В –µ –њ–Њ–і–Њ–±–љ–Њ –љ–∞ —А–µ—И–∞–≤–∞–љ–µ—В–Њ¬†–љ–∞¬†–њ—А–Њ–±–ї–µ–Љ–∞¬†NP=P –≤ –Ї–Њ–Љ–њ—О—В—К—А–љ–Є—В–µ –љ–∞—Г–Ї–Є, –Ї–Њ–є—В–Њ —Б—В–∞–≤–∞ –µ–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї–љ–Њ –њ–Њ-—Б–ї–Њ–ґ–µ–љ —Б —Г–≤–µ–ї–Є—З–∞–≤–∞–љ–µ—В–Њ –љ–∞ –±—А–Њ—П –љ–∞ –∞—В–Њ–Љ–Є—В–µ. –Ґ–µ–Ј–Є –њ—А–Њ–±–ї–µ–Љ–Є –Љ–Њ–≥–∞—В –±—К—А–Ј–Њ –і–∞ —Б—В–∞–љ–∞—В –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Є –Ј–∞ –Є–Ј—З–Є—Б–ї—П–≤–∞–љ–µ –≤ –≥–Њ–ї–µ–Љ–Є –Љ–∞—Й–∞–±–Є, –љ–Њ –Є–Ј—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є—В–µ —Г—Б—В–∞–љ–Њ–≤—П–≤–∞—В, —З–µ –Ј–∞ –љ—П–Ї–Њ–Є –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є –њ—А–Њ–±–ї–µ–Љ—К—В –µ –љ–µ–Њ—З–∞–Ї–≤–∞–љ–Њ –њ—А–Њ—Б—В.
"–Ґ–Њ–≤–∞ –±–µ—И–µ –Љ–љ–Њ–≥–Њ –Є–Ј–љ–µ–љ–∞–і–≤–∞—Й–Њ, —В—К–є –Ї–∞—В–Њ —В–Њ–Ј–Є –њ—А–Њ–±–ї–µ–Љ –Ї–∞—В–Њ —Ж—П–ї–Њ —Б–µ –Ј–љ–∞–µ, —З–µ –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ –µ –љ–µ–≤—К–Ј–Љ–Њ–ґ–µ–љ –Ј–∞ —А–µ—И–∞–≤–∞–љ–µ –Є –љ–µ –Є–Ј–≥–ї–µ–ґ–і–∞—И–µ –Њ—З–µ–≤–Є–і–љ–Њ –Њ–њ—А–Њ—Б—В—П–≤–∞–љ–µ, –њ—А–µ–і–Њ—Б—В–∞–≤–µ–љ–Њ –Њ—В —В–µ–Ј–Є –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є, —В—К–є –Ї–∞—В–Њ —В–µ –љ—П–Љ–∞—В —В—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–Є —Б–Є–Љ–µ—В—А–Є–Є", –Њ–±—П—Б–љ—П–≤–∞ –§–ї–Є–Ї–µ—А.
 –†–µ—И–µ–љ–Є–µ –љ–∞ –ї–∞–±–Є—А–Є–љ—В–∞, –Љ–∞—А–Ї–Є—А–∞–љ–Њ –≤ —З–µ—А–≤–µ–љ–Њ. –Ъ—А–µ–і–Є—В: University of Bristol
–†–µ—И–µ–љ–Є–µ –љ–∞ –ї–∞–±–Є—А–Є–љ—В–∞, –Љ–∞—А–Ї–Є—А–∞–љ–Њ –≤ —З–µ—А–≤–µ–љ–Њ. –Ъ—А–µ–і–Є—В: University of Bristol
–§–ї–Є–Ї–µ—А –Њ—В–±–µ–ї—П–Ј–≤–∞, —З–µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В—В–∞ –Ј–∞ —А–∞–Ј—А–∞–±–Њ—В–≤–∞–љ–µ –љ–∞ —В–∞–Ї—К–≤ –Љ–∞—А—И—А—Г—В –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П –≤ –ї–∞–±–Њ—А–∞—В–Њ—А–µ–љ –Љ–µ—В–Њ–і, –Є–Ј–≤–µ—Б—В–µ–љ –Ї–∞—В–Њ —Б–Ї–∞–љ–Є—А–∞—Й —В—Г–љ–µ–ї–µ–љ –Љ–Є–Ї—А–Њ—Б–Ї–Њ–њ, –Ї—К–і–µ—В–Њ —Г–ї—В—А–∞–Њ—Б—В—К—А –≤—А—К—Е —Б–µ –љ–∞—Б–Њ—З–≤–∞ –≤—К—А—Е—Г –Љ–∞—В–µ—А–Є–∞–ї, –Ј–∞ –і–∞ —Г—Б–µ—В–Є –∞—В–Њ–Љ–Є—В–µ –µ–і–Є–љ –њ–Њ –µ–і–Є–љ –Є –і–∞ –Є–Ј–≥—А–∞–і–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ –љ–∞ –∞—В–Њ–Љ–љ–Њ –љ–Є–≤–Њ. –°—К–Ј–і–∞–≤–∞–љ–µ—В–Њ –љ–∞ –љ—П–Ї–Њ–Є —Б–ї–Њ–ґ–љ–Є –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є—П, –Ї–∞—В–Њ —В–µ–Ј–Є –љ–∞ —Б–∞–Љ–Є—В–µ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є, –Љ–Њ–ґ–µ –і–∞ –Њ—В–љ–µ–Љ–µ –і–Њ –µ–і–Є–љ –Љ–µ—Б–µ—Ж, –љ–Њ –∞–Ї–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞–Љ–µ—А–Є –њ–Њ-–µ—Д–µ–Ї—В–Є–≤–µ–љ –њ—К—В, –Ї–Њ–є—В–Њ –Њ–±—Е–≤–∞—Й–∞ –≤—Б–µ–Ї–Є –∞—В–Њ–Љ, —В–Њ–≥–∞–≤–∞ —В–Њ–≤–∞ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –љ–∞–Љ–∞–ї–µ–љ–Њ –љ–∞–њ–Њ–ї–Њ–≤–Є–љ–∞, –Ї–∞–Ј–≤–∞ –§–ї–Є–Ї–µ—А.
–Ґ–Њ–є —Б—К—Й–Њ —В–∞–Ї–∞ —Б–Љ—П—В–∞, —З–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ –Ї—А–Є—Б—В–∞–ї–љ–Є –Ї–∞—В–∞–ї–Є–Ј–∞—В–Њ—А–Є –Ј–∞ –њ—А–Њ–Љ–Є—И–ї–µ–љ–Є —Е–Є–Љ–Є—З–µ—Б–Ї–Є –њ—А–Њ—Ж–µ—Б–Є, –Ї–Њ–Є—В–Њ —Б–∞ –њ–Њ-–µ—Д–µ–Ї—В–Є–≤–љ–Є –Њ—В –љ–∞—Б—В–Њ—П—Й–Є—В–µ –Љ–µ—В–Њ–і–Є –Є —Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ —Г—Б–Ї–Њ—А—П–≤–∞—В –Є–ї–Є –љ–∞–Љ–∞–ї—П–≤–∞—В —А–∞–Ј—Е–Њ–і–Є—В–µ –Ј–∞ –њ–Њ–ї—Г—З–∞–≤–∞–љ–µ –љ–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є —Б—К–µ–і–Є–љ–µ–љ–Є—П. –Э–Њ¬†–§–ї–Є–Ї–µ—А —Б–Љ—П—В–∞, —З–µ –Є –і—А—Г–≥–Є –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П –Љ–Њ–≥–∞—В –і–∞ —Б—В–∞–љ–∞—В –Њ—З–µ–≤–Є–і–љ–Є —Б –≤—А–µ–Љ–µ—В–Њ:
"–Э–∞–і—П–≤–∞–Љ–µ —Б–µ, —З–µ –љ–∞–є-–Є–љ—В–µ—А–µ—Б–љ–Є—В–µ –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П —Б–∞ –љ–µ—Й–∞, –Ј–∞ –Ї–Њ–Є—В–Њ –љ–µ —Б–Љ–µ —Б–µ —Б–µ—В–Є–ї–Є."
–°–њ—А–∞–≤–Ї–∞:¬†Hamiltonian cycles on Ammann-Beenker Tilings,¬†Phys. Rev. X,¬†Shobhna Singh, Jerome Lloyd, and Felix Flicker;¬†https://journals.aps.org/prx/accepted/9c077K95P1d1d60727e054a929069cafd5b559c87¬†
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:¬†
Incredibly complex mazes discovered in structure of bizarre crystals, New Scientist
Physicists Have Created The World's Most Fiendishly Difficult Maze, ScienceAlert
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞
–§–Є–Ј–Є–Ї–∞
–Я—А–µ–і—Б–Ї–∞–Ј–∞–љ –µ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –њ–ї–Њ—З–Ї–∞—В–∞ "—И–∞–њ–Ї–∞—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ"

–§–Є–Ј–Є–Ї–∞
–§–Є–Ј–Є—Ж–Є –њ–Њ—Б—В–Є–≥–∞—В —Б–≤—А—К—Е–њ—А–Њ–≤–Њ–і–Є–Љ–Њ—Б—В –Є –Њ—Й–µ –љ–µ—Й–Њ –Њ—В –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ - –Љ–µ–ґ–і—Г –і–≤–∞ —Б–≤—П—В–∞





















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews