В математиката прости уравнения могат да генерират сложна еволюция във времето и завладяващи самоповтарящи се модели (патерни) в пространството. Един от известните примери е множеството на Манделброт, кръстен на математика Беноа Манделброт, въвел понятието "фрактал" за подобни форми.
Това множество се основава на едно квадратно уравнение само с един параметър и една променлива. Очарователните фрактални модели на множеството Манделброт привличат вниманието далеч отвъд математиката.
Увеличение върху множеството на Манделброт. Кредит: Wikimedia Commons
Статия на Ралф Анджеяк (Ralph Andrzejak), озаглавена Chimeras confined by fractal boundaries in the complex plane („Химери, ограничени от фрактални граници в комплексната равнина“), е част от специално издание на списанието „ Хаос“ в памет на руския професор Вадим С. Анищенко, публикувано на 3 май, 2021. Анджеяк е ръководител на групата за нелинейни анализи на времеви редове в Департамента по информационни и комуникационни технологии (DTIC) на Университета Помпей Фабра (UPF).
Работата обобщава множеството на Манделброт за четири квадратни уравнения. Фигурата, показана по-долу, е пример за моделите, генерирани чрез този подход.
Фрактални модели, генерирани от набор от четири квадратни уравнения. Сивите цветове показват дивергенция до безкрайност. Несивите цветове кодират различни състояния на синхронизация. Кредит: UPF
Пътуване през много порядъци
Анджеяк отбелязва, че „сложността на фракталните модели може да се види, когато се приближим до все по-малки детайли“, което авторът илюстрира на изображението по-долу. Той обяснява изображението, като казва, че „общо погледнато моделът, показан в горния ляв панел на фигурата, прилича на класическото множество на Манделброт. Веднага след като разгледаме детайлите, можем да видим модели, които не могат да бъдат намерени в множеството Манделброт. За да видим тези подробности по-добре, ние увеличаваме квадрата, за да създадем следващия панел".
„Итеративно увеличение на фрактални модели. Отляво надясно и отгоре надолу следващите панели увеличават квадратите на съответните предишни панели. Първата фигура по-горе се появява отново, тук като петата стъпка в увеличението. Кредит: UPF
Авторът използва сравнение, за да подчертае, че тези модели наистина са от много порядъци. Той заявява, че „увеличението, приложено към дванадесетте панела, съставляващи изображението, съответства на раздуването на атом до размера на автомобил“.
„Докато увеличаваме и увеличаваме размера на изображението, виждаме, че има богато разнообразие от естетически интригуващи форми и форми. Моделите, които открихме, може да изглеждат по-малко филигранни и по-малко подредени, но са по-разнообразни от тези, намерени в множеството на Манделброт".
Взаимодействие на фрактали и синхронизация
Но има повече от фрактални модели, за да се подходи към предложението на Анджеяк. Тъй като авторът използва четири уравнения вместо едно, той също е успял да изучи синхронизацията в рамките на тези фрактални модели. Как можем да разберем това? Andrzejak обяснява, като казва, че
„Множеството на Манделброт се основава на едно уравнение с един параметър и една променлива. Можем да си представим тази променлива като малка топка, която се движи по повърхността на голяма кръгла маса. Какво ще се случи с тази топка зависи от параметъра на уравнението. За някои стойности на този параметър топката се движи и винаги е на масата. Множеството от всички тези стойности на параметрите, за които топката остава на масата, е това, което определя множеството на Манделброт. Напротив, за останалите стойности на параметрите топката пада от масата в даден момент от времето".
Анджеяк продължава, като казва, че „може да се мисли, че четирите уравнения, които използваме, описват движението не само на една, а на четири топки по повърхността на масата. Тъй като уравненията са свързани, топките не могат да се движат свободно. Те обаче се привличат, както Слънцето, Земята и Луната се привличат помежду си чрез гравитацията".
Изследователят добавя, че „в резултат на това привличане четирите топки могат да показват различни форми на синхронизация. Двете крайности са: Четирите топки се движат заедно по едни и същи траектории или всяка топка следва своя".
„Най-важното, отвъд тези крайности, е намирането на така наречената частична синхронизация. Например две топки могат да се движат в синхрон заедно, докато другите две топки остават несинхронизирани от това движение", подчертава Анджеяк.
Въпрос от голямо значение за динамиката на реалния свят
На въпроса дали въпросният математически модел може да има отношение към динамиката на реалния свят, Анджеяк отговаря:
„Да. Абсолютно. Най-добрият пример е мозъкът. Ако всички наши неврони се синхронизират или изчезнат, мозъкът ни вече не може да си свърши работата. Нашият мозък може да работи правилно само ако някои неврони се синхронизират, докато други неврони остават несинхронизирани. Частичната синхронизация е от съществено значение за правилната работа на мозъка".
Авторът свързва това със своята работа, като казва: „ние демонстрираме как е възможно да се установи частична синхронизация в много прост модел и освен това показваме как тази частична синхронизация се ограничава във фракталните граници чрез пълна синхронизация и десинхронизация“.
„Ако изучим основните механизми на частичната синхронизация в много прости модели, това гнще помое да помогне да се разбере как тя [синхронизацията] се установява и как може да се поддържа стабилна в такива сложни системи като човешкия мозък“, заключава авторът.
Справка: “Chimeras confined by fractal boundaries in the complex plane ” by Ralph G. Andrzejak, 3 May 2021, Chaos.
DOI: 10.1063/5.0049631
Източник: A New Bridge Between the Geometry of Fractals and the Dynamics of Partial Synchronization, Universitat Pompeu Fabra - Barcelona
Още за множеството Манделброт
Алгебричните фрактали възникват в изследването на нелинейни динамични системи, затова се наричат и динамични, и нелинейни. Те са обект на особено внимание, защото възпроизвеждат огромно богатство от геометрични фигури само от един съвсем прост алгоритъм и са тясно свързани със съвременната теория на хаоса.
Тъй като.се развиват в комплексната равнина, нека си припомним какво представляваха комплексните числа.
За да се построи фракталът например на Манделброт имаме нужда от комплексни числа. Комплексните числа се състоят от две части - реална и имагинерна, а цялото комплексно число се означава така: z =a+bi , като i се нарича имагинерна единица, защото ако се повдигне на квадрат, получаваме -1, т. е. i2 = –1; a и b са реални числа, като a се нарича реална, а b се нарича имагинерна част на числото.
Ако b = 0, то вместо a + 0i пишем просто a - т.е. реалните числа са частен случай на комплексни числа.
Събирането и изваждането стават по правилото (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение - по правилото (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (тук се използва, че i2 = –1). Тези действия ще се използват основно в разглежданите по-късно фрактали.
 |
 |
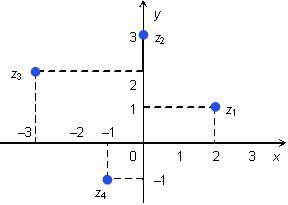
| z1 = 2+i; z2 = 3i; z3 = --3+2i; z4 = -1-i; | |z1| = √5; |z2| = 3; |z3| = √13; |z4| = √2; |
Комплексните числа може да се събират, изваждат, умножават, делят и всички останали алгебрични действия, но не могат да се сравняват. Комплексно число може да се представи като точка в Декартовата равнина, в която x координата е реалната част, а y е коефициентът на имагинерната част b.
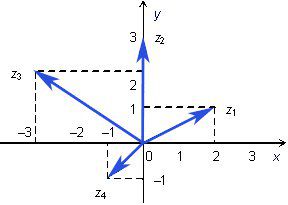
Комплексните числа имат удобно и нагледно геометрично представяне - числото z = a + bi може да бъде изобразено и като вектор с координати на върха (a, b) . Сумата от две комплексни числа се представя като сумата на съответните вектори по правилото на успоредника. По теоремата на Питагор дължина на вектора с координати (a, b) е равна на 
Тази величина се нарича модул на комплексното число z = a + bi и се означава с |z|. Ъгълът, който този вектор сключва с положителната посока на ос х (отчетен обратно на часовниковата стрелка) се нарича аргумент на комплексното число z . Аргументът не е еднозначно определен, а точно само до добавянето на величина, кратна на 2π радиана (или 360°) - ясно е, че пълен оборот около началото на координатите няма да промени вектора.
Основни принципи
Има различни видове нелинейни фрактали, но в най-общия случай алгебричния фрактал се задава с итерации на полином
Нека f(z) е полином , а z0 комплексно число. Да разгледаме следната последователност:
z0, z1=f(z0), z2=f(f(z0))=f(z1), z3=f(f(f(z0)))=f(f(z1))= f(z2), ...
В зависимост от началната точки z0 , при изследване на поведението на тази последователност, когато n клони към безкрайност, тази последователност може да се държи по различен начин:
- да клонни към безкрайност
- да клонни към крайно число,
- да проявява циклично поведение в някакви граници, например: z1, z2, z3, z1, z2, z3...
- да се държи хаотично, т.е. да не показва нито един от горните три типа поведение.
Множество на Жюлиа
| Да си представим комплексната равнина, цялата изпълнена с точки, съответстващи на комплексните числа. Да начертаем окръжност около началото на координатната системас радиус 1. Някои точки ще попаднат вътре в окръжността (червените), а други (зелените) - вътре. Да ги повдигнем на квадрат. |  |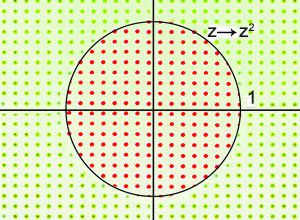
| Резултатът от последователните итерации на повдигане на степен е, че червените точки остават вътре в окръжността, а зелените се разбягват далече от нея. Тази окръжност е запълнено множество на Жюлиа, получено от итерации, извършващи преобразувания повдигане на квадрат. Точните извън множеството на Жюлиа, след неограничени преобразувания повдигане на квадрат отиват в безкрая. |  |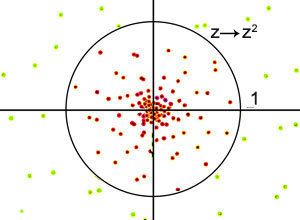
Ако алгоритъмът се промени на z → z2+c, където c е някакво комплексно число, за всяко различно c , очертанията на формата на множеството на Жюлиа започва да се променя. Колкото е по-голямо по модул c , толкова то силно се отклонява от формата на кръг. Добавянето на параметъра c към точките от комплексната равнина "ще запрати" някои от тях към безкрайността, а други ще насочи към центъра. Така ще се образуват нови разнообрази форми:
 |
 |
 |
 |
 |
 |
 |
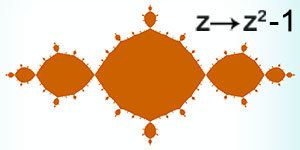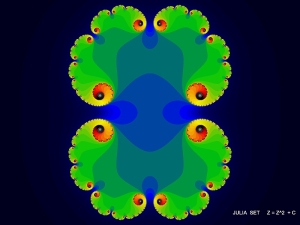
Симетрията в очертанията на запълненото множество на Жюлия говори за липса на имагинерна част, а завихрянията - за наличието й. | |
Полиномът f(z) може да се разглежда като запълнено множество на Жюлиа, множеството точки, които не се стремят към безкрайност. А множеството на Фату е дополнение на множеството на Жюлиа и ако последното е затворено множество, то множеството на Фату е отворено.
Точките, лежащи на границата между двете множества имат свойството при много малка промяна на позицията, характерът на поведението им драстично да се изменя. Границата на запълненото множество на Жюлиа има фрактални характеристи със самоподобни части, тя представлява обикновеното множество на Жюлиа.
Графичните интерпретации
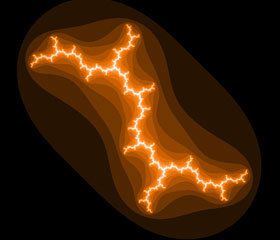
Това красиво оцветено изображение не е точно самото множество на Жюлиа, което всъщност се състои от само от точки и не може да бъде изрисувано така. На картинката се виждат точките от околността на множеството на Жюлиа и колкото е по-ярка точката, толкова е по-близко до множеството на Жюлиа и толкова повече итерации са й необходими за да се отдалечи.
 |
|
||||||||||
| При c = i множеството на Жюлиа се превраща в дендрит - дървовидна структура, срещаща се в минералогията, и във физиологията, а тук напомня на светкавица (те също имат фрактална структура | Как ще изглежда множеството на Жюлиа, ако се смени степента от формулата z → z2+c вместо 2, с 3, 4, 5, 6. |
||||||||||
Връзката между множествата на Жюлиа и множеството на Манделброт
Математиците Жюлиа и Фату открили, че за всеки параметър c се получават два вида фрактални изображения:
- Множеството на Жюлиа може да бъде едносвързана фигура или
- т.н. прах на Фату (хомеоморфен на праха на Кантор), който се състои от безкраен брой несвързани една с друга точки, разхвърлени подобно на прашинки и има размерност нула.
Понятията "едносвързано" и "хомеоморфно" са от областта на топологията и с тях може да се запознаете в темата "Хипотезата на Поанкаре".
Ако нанесем всяка точка от комплексната равнина със стойност параметъра c, за който множеството на Жюлиа е едносвързано и прескочим точките със стойности на c, които дават несвързани множества, резултатът ще бъде фракталът на Манделброт. На всяка точка (или координата) от множеството на Манделброт съответства някакъв фрактал Жюлиа.
Комплексното множество на Манделброт
Множеството на Манделброт, което било построено от Беноа Манделброт, навярно е първата асоциация, възникваща у хората, когато чуят "фрактал".
Този фрактал се генерира по същата прост алгоритъма като фрактала на Жюлиа
z → z2+c,
Но тук акцентът е другаде, защото множеството на Манделброт се състои само от точки, за които множеството на Жюлиа може бъде едносвързано.
Определяне на множеството на Манделброт. Критерий за едносвързаност на множеството на Жюлиа
Ако определим критерия за едносвързаност на множеството на Жюлиа, ще можем да изобразим и множеството на Манделброт. С определянето на този критерий са се справили и Жюлиа и Фату. Те са открили, че този този на пръв поглед труден проблем може да бъде решен с прости сметки.
Да разгледаме последователността от стойности на zn, получени от формулата
Ако тя не клони към безкрайност, то асоциираното със същата стойност на параметъра c множество Жюлиа ще бъде едносвързано и точката c ще принадлежи на множеството на Манделброт.
На всяка точка от множеството на Манделброт съответства фрактал на Жюлиа.
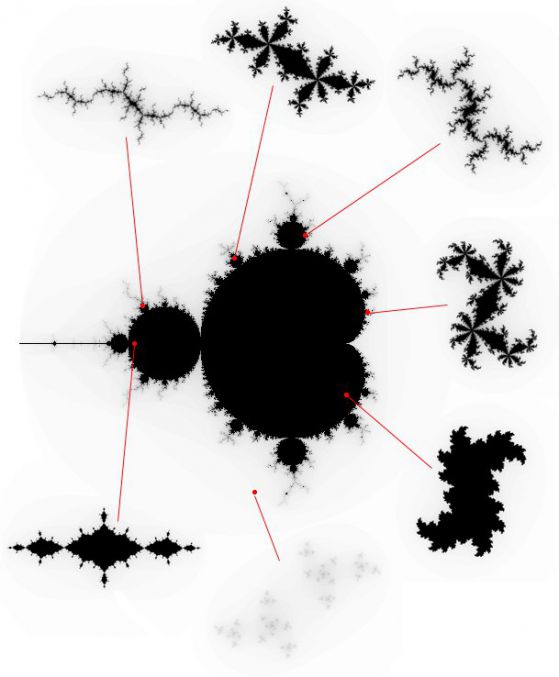
Как се изчертава множеството на Манделброт
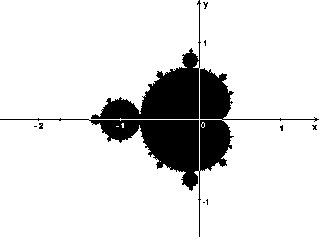За да построим този знаменит фрактал итерациите се изпълняват за всяка стартова точка C в правоъгълна или квадратна област - подмножество на комплексната плоскост. Итерационият процес продължава дотогава, докато Z[i] не излезе извън границите на окръжност с радиус 2, центърът на която лежи в точката (0,0), (това означава, че атракторът на динамичната система се намира в безкрайността), или след достатъчно голям брой итерации (например 200-500) Z[i] започне да клони към някаква точка от окръжността. В зависимост от количеството итерации, в течениe на които Z[i] остава вътре в окръжността, може да се определи цвета на точка C (ако Z[i] остава вътре в окръжността в течение на достатъчно количество итерации, итерационния процес се прекратява и тази точка се оцветява в черно). Към множеството на Манделброт принадлежат точки, които в течение на безкраен брой итерации не клонят към безкрайност (черни точки).
Точките, принадлежащи на границата множеството (именно там възникват сложни структури) клонят към безкрайност за крайно число итерации, а точките лежащи извън пределите на множеството, клонят към безкрайност след няколко итерации.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари