Да приличаш на себе си

Много неща около нас изглеждат подобни независимо от това, колко ги увеличаваме - клоните и листата на дърветата, планините, облаците, реките, кръвоносните съдове и навсякъде в природата. Когато част от някоя фигура е подобна на цялата фигура, наричаме това самоподобие. 

ПРОЧЕТЕТЕ ПРЕДИ ТОВА:

Фракталите. Въведение

Точно самоподобие

При много фрактали, самоподобието е очевидно, може ясно да се види във фигурите по-долу. Всеки от тези фрактали е съставен от по-малки версии на себе си. При увеличение, се оказва, че частите са идентични на цялото изображение. Такива са геометричните фрактали.

Драконът от книгата "Юрски парк" на Майкъл Крайтън, (дракон на Хартер-Хейтуей)	Пентагонът на Албрехт Дюрер	Kривaта на Леви	Триъгълникът на Серпински

Триъгълникът (решетката, салфетката) на Серпински, както и цяла серия фрактали като килимът (квадратът), кривата на Серпински са измислени от полския математик Вацлав Франциск Серпински през 1915г. Серпински е учен с изключителен принос към теорията на множествата, теорията на числата, теорията на функциите и топологията. Тази анимация показва ясно точното самоподобие в този фрактал - триъгълника на Серпински, може да я задвижите с "play".

play pause

	Това е анимация, демонстрираща самоподобието и на тримерния триъгълни (тетраедър) на Серпински . Може да я задвижите с "play". Изчакайте, достатъчн е да поставите само мишката, без натискане,
play pause

Приблизително самоподобие

Понякога, фигурата не е толкова очевидно самоподобна и в този случай имаме приблизително самоподобие. Например, в известния фрактал на Манделброт не се виждат идентичните изображения. Обаче, когато започнете да увеличавате, ще се сблъскате с малки версии на фрактала на всички нива на увеличение.

Най-добре това приблизително самоподобие се забелязва на видео, като "потъваме" в движение във фрактала на Манделброт. Поставете мишката върху изображението, за да се приближите:

Брауновото самоподобие

Горните примери на фрактали са точни или детерминирани фрактали. Всички те са изградени върху ясно определено геометрично правило или формула.

В природата по-честно срещани от точните фрактали са т. н. случайни фрактали. В подреждането на техните елементи има някаква доза случайност. 

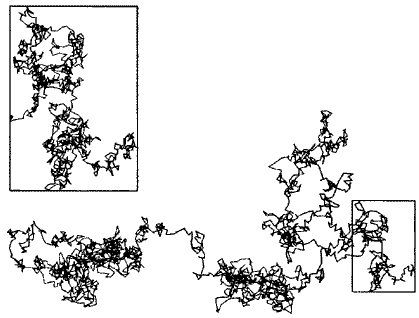
През 1828 г. Роберт Браун изучавайки движението на микроскопични частици във водата, открил, че то е случайно и хаотично. Траекторията на частиците изпълняващи Брауново движение е прост случаен фрактал. 

Ако се свържат последователните позиции на една частица на всеки 30 секунди с прави линии, се получава траектория от отсечки, разположени произволно в пространството. Ако се намали интервала между измерванията 100 пъти, на мястото на всяка отсечка от линията ще се появи начупена линия също толкова сложна, колкото оригиналното изображение. 

Манделброт в "Фракталната геометрия на природата" набляга на факта, че при постепенно увеличаване на мащаба, дължината на наблюдаваната крива на Брауновото движение се увеличава до безкрайност, подобно на дължината на крайбрежието на Англия.

Следите от Брауновото движение на частиците в края на крайщата ще изпълни почти цялата равнина. От това следва, че размерността на траекторията съвпада с размерността на равнина, т.е  фракталната размерност е D=2., въпреки, че топологично траекторията на Брауновите частици е с размерност 1. Този факт ни дава основание да класифицираме следите на брауновото движение като фрактал.

Фрактални клъстери или DLA (Diffusion-Limited Aggregation)

Поставете мишката върху изображението, за да се задвижи процеса DLA.

Друг пример на случаен фрактал, по-сложен, но също толкова разпространен в природата като горния, се получава в т.н. процес "дифузия, ограничена от агрегация" - DLA (Diffusion-Limited Aggregation).

"Дифузия", защото частиците съставляващи структурата скитат наоколо преди случайно да се прикачат ("струпват") към структурата. "Ограничена", защото се приема, че частиците са в ниски концентрации, така че не влизат в контакт помежду си и структурата расте частица по частица.

Тя може да се моделира по следния начин: Да си представим сфера (окръжност в двумерния случай) с достатъчно голям радиус, от повърхността на която от време на време на случайни места се появяват частици, които блуждаят вътре в сферата. В центъра й се намира т.н. "клъстер" (зародиш). При сблъсък блуждаещата частица "прилепва" към него и повече не се движи. После прилепва следващата частица и така до безкрайност. В резултат се образува една силно пореста структура. С разрастването й, броят на порите и размерите им се увеличават. В двумерния случай фракталната размерност на такъв клъстер е около 1.7.

Зародишът (семенцето, атракторът) може да е точка, линия, стените на кутия.

Може да се въведе т.н. коефициент на лепкавост, който представлява вероятността за залепване на частицата. Във всичките примери досега, ако блуждаещата частица се удари в съществуващата структура, тя винаги остава (лепкавост = 1). Промяната на този коефициент ще доведе до по-космати и по-солидни форми.

Кл = 0,2	Кл =  0,05	Кл = 0,01

Може частиците да са оцветени по реда, в който се слепват, а може и размерът им да намалява като първи се прикрепят най-едрите частици.

Такъв процес се нарича агрегация, а когато частиците се движат към растящия клъстер в условията случайно движение — това всъщност е DLA. Този процес е крайно неустойчив. С негова помощ може лесно да се обяснят някои свойства на растеж на фракталните структури. В природата подобни фрактални клъстери се срещат много често. Така, например, растат коралите, мазолите, кристалите в наситен разтвор, снежинките, така се оформя пътят на мълнията, така се слепва прах или сажди и т. н. .

Продължение:

Скритите измерения на фракталната размерност

Итерации

Рекурсия

Видове фрактали

Алгебрични (динамични, нелинейни) фрактали

Основни понятия и лексика

• Фрактали
  • дракон на Хартер-Хейтуей
  • пентагонът на Албрехт Дюрер
  • кривa на Леви
  • триъгълник на Серпински
  • фрактал на Манделброт
  • детерминирани фрактали
  • случайни фрактали
• Самоподобие
  
  • Точно самоподобие
  • Приблизително самоподобие
  • Брауновото самоподобие
  • Фрактални клъстери или DLA 
  • Diffusion-Limited Aggregation
    • агрегация
    • коефициент на лепкавост
• Вацлав Франциск Серпински
• Роберт Браун
• Беноа Манделброт

Източници:

Фрактальная геометрия природы, Мандельброт Б.

Fractal Geometry, Yale University, Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger

Фрактальный рост, Л.М. Сандер (doc)

Ограниченная диффузия

Принцип Кюри и ограниченная диффузией агрегация © Л.М. Мартюшев, Л.Г. Горбич

DLA - Diffusion-Limited Aggregation, Paul Bourke