Точно както молекулите са съставени от атоми, така и в математиката всяко естествено число може да се раздели на своите прости множители - тези, които се делят само на себе си и на 1. Математиците искат да разберат как са разпределени простите числа по числовата линия с надеждата да открият принцип за организиране на атомите на аритметиката.
"На пръв поглед те изглеждат доста случайни", коментира Джеймс Мейнард (James Maynard), математик от Оксфордския университет. "Но всъщност се смята, че в простите числа има скрита структура."
В продължение на 165 години математиците, търсещи тази структура, се фокусират върху хипотезата на Риман. Нейното доказване би предложило Розетски камък за разшифроване на простите числа - както и награда от 1 млн. долара от Института по математика "Клей". Сега, в препринт, публикуван онлайн наскоро, Мейнард и Лари Гът (Larry Guth) от Масачузетския технологичен институт правят стъпка в тази посока, отхвърляйки някои изключения от хипотезата на Риман. Резултатът едва ли ще спечели паричната награда, но представлява първият напредък от десетилетия насам по най-големия неразрешен проблем на математиката и обещава да предизвика нов напредък в цялата теория на числата.
"Това е сензационен пробив", отбелязва Алекс Конторович (Alex Kontorovich), математик от университета Рутгерс. "В това доказателство се съдържат куп нови идеи, които хората ще използват години наред."
Да се предвиди къде точно ще се появи следващото просто число на редицата на числата е предизвикателство, но да се опише съвкупността от прости числа в големи интервали е изненадващо просто. В края на 1700 г., на 16-годишна възраст, немският математик Карл Фридрих Гаус забелязва, че честотата на простите числа изглежда намалява с увеличаването им, и изказва предположението, че те се увеличават по проста формула: броят на простите числа, по-малки или равни на X, е приблизително X, разделен на естествения логаритъм на X. Оценката на Гаус се е запазила впечатляващо добре. Доколкото математиците могат да преценят, действителният брой на простите числа се колебае малко над и под тази крива до безкрайност. Фактът, че известните числа следват толкова точно една проста формула, предполага, че числата не са напълно случайни; трябва да има някакви дълбоки връзки, които да определят мястото на появата им.
Но математиците искат да знаят точно колко добре се потвърждава предположението на Гаус - и защо. През 1859 г. Бернхард Риман, друг известен немски математик, търси помощ от друга функция, която сега се нарича Риманова дзета функция. За входни данни функцията приема комплексни числа, които са комбинация от реални числа и това, което математиците наричат "имагинерни": нормално число, умножено по квадратния корен от -1. Изглежда, че функцията улавя несъответствията между кривата на Гаус и реалното разпределение на простите числа. Местата, където функцията на Риман е равна на нула - наричани дзета-нули - описват директно колебанията на грешките около кривата на Гаус.
Дзета функцията на Риман
Риман разбира, че дзета функцията е ключът към теоремата за разпределението на простите числа, но за да се приложи този подход, трябва да се разшири, да се определи дзета функцията не само за реални, но и за комплексни променливи.
Има още едно нещо, което може да се направи. С помощта на комплексния математичен анализ, може да се разшири областта на определение на дзета-функцията на Ойлер така, че за числа по-малки или равни на 1 функцията да приема крайни стойности. С други думи, има начин да се определи нова функция, която ще наречем ζ (x) :
ζ(x) = 1/1x + 1/2x + 1/3x + 1/4x + … .
За x > 1 и за x < 1 функцията ζ(x) ще приема определени крайни стойности. Този метод се нарича аналитично продължение и новата функция, която се получава, се нарича дзета-функцията на Риман. Създаването на тази нова функция приемаща крайни стойности и за x < 1 се състои в изваждането от несходящия ред на друг несходящ ред. Така от безкрайността, получаваща се от първата разходяща сума минус безкрайността, която дава втората разходяща сума, се получава нещо крайно.
Риман разширява определението на ζ (x) за всички комплексни числа освен 1. Единицата е изключена, защото за x = 1, стойността на дзета-функцията става безкрайна.
Интуицията на Риман е доста забележителна при свързването на свойствата на непрекъсната функция на комплексна променлива със свойствата на простите числа, които са реални и дискретни. По-конкретно, Риман показва, че броят на простите числа, по-малки от x, е свързан с точките, в които дзета функцията е равна на нула - тези точки са известни като нули на функцията.
Тривиални и нетривиални нули
Риман успял да покаже, че разпределението на простите числа зависи от това къде дзета-функцията се нулира. Тя има така наречените тривиални нули в четните отрицателни числа (–2, –4, –6, …). Те са тривиални в смисъл, че тяхното съществуване може да се докаже сравнително лесно (например използвайки функционалното уравнение).
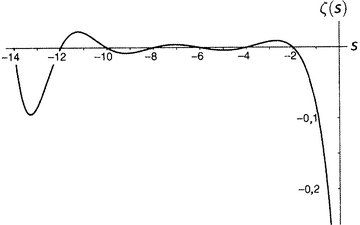
Всички останали нули се наричат нетривиални. Задачата се състои в това, да се опишат всички останали нули на дзета-функцията. А всички нетривиални нули на дзета-функцията се получават за комплексни числа. Те лежат на критичната линия, а реалната им част, равна на 1/2.
Това е и забележителната хипотеза на Риман.
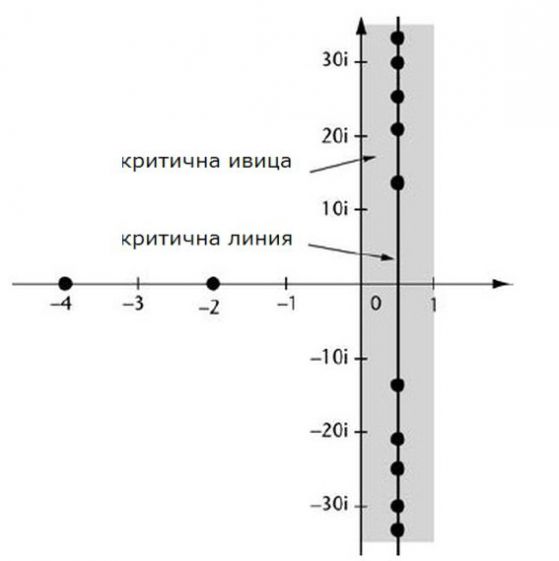
Нулите на дзета-функцията, критичната линия и критичната ивица
Хипотезата става известна като хипотезата на Риман и е ключът към разбирането на разпределението на простите числа и все още няма доказателство, че няма изключения от този модел.
Ако хипотезата му е вярна, това означава, че привидно случайните колебания в разпределението на простите числа са ограничени и не оставят големи струпвания или пропуски в разпределението им по линията на числата. Всяко доказателство на хипотезата на Риман би било прозорец към тайния часовников механизъм, управляващ неравномерната последователност на простите числа. Това би дало възможност за "обратно конструиране на генератора на случайни числа на простите числа", смята Максим Радзивил (Maksym Radziwill), математик от Северозападния университет.
Досега математиците са използвали компютри, за да тестват повече от 10 трилиона нетривиални дзета-нули - и всички те лежат точно на 1/2. Но нито едно емпирично доказателство няма да задоволи математиците: Те искат официално доказателство, че нулите не могат да лежат никъде другаде. Въпреки че никой не подозира, че хипотезата на Риман е невярна, "доказателството дава много повече от това, че едно твърдение е вярно", обяснява Мейнард. "То дава разбиране защо е вярно, така че имате нова мощна техника за разбиране на простите числа."
След 165 години математиците продължават да са "в пълна безизходица" по отношение на това как могат да докажат хипотезата на Риман, казва Мейнард. "Нямаме дори правдоподобна линия на атака." Затова те прибягват до по-малки парченца от задачата, като определят къде не може да има дзета нули.
Математиците вече знаят, че нетривиалните дзета нули са ограничени между 0 и 1.
Те също така знаят за огледалната симетрия около 1/2, при която изключването на дзета-нули в 3/4 би ги изключило и в 1/4. Така че някои техники се фокусират върху областта от 1/2 до 3/4, докато други работят по-добре между 3/4 и 1. Това оставя малка, но обезпокоителна възможност много нули да се крият точно в 3/4.
Най-добрата граница за това колко нули могат да се крият в 3/4 е дадена от британския математик Алберт Ингам през 1940 г. Оттогава никой не се е справил по-добре.
"Беше малко неприятно, че тази [граница] не можеше да бъде намалена", разказва Радзивил. "По принцип никой не работеше по този въпрос, защото всички се отказаха."
С изключение на Мейнард, 37-годишен виртуоз, който специализира в аналитичната теория на числата, за която през 2022 г. печели медала "Фийлдс" - най-престижната награда в областта на математиката. В посветените на проблема петъчни следобедни мисловни сесии той се връща към нея отново и отново през последното десетилетие, но без резултат. На среща на Американското математическо общество през 2020 г. той търси помощта на Гът, който специализира в техника, известна като хармоничен анализ, която черпи от идеите във физиката за разделяне на звуците на съставните им ноти. Гът също се занимава с проблема в продължение на няколко години. Малко преди да се откаже, двамата с Мейнард правят пробив. Заимствайки тактики от съответните си математически диалекти и обменяйки идеи до късно през нощта чрез верига от имейли, те прилагат някои нестандартни ходове, за да преодолеят най-накрая ограничението на Ингам.
Радзивил посочва, че работата представлява първата нова идея в търсенето на дзета-нули от 50 години насам.
"Това всъщност може да даде нов старт на една област, която дълго време беше пренебрегвана", обяснява той. "Искам да кажа, че може да настъпи ренесанс."
Подобрената граница не помага на математиците да докажат Римановата хипотеза като цяло. Но Радзивил и Конторович очакват, че резултатът ще се разпространи в цялата теория на числата. Новото ограничение веднага позволява на математиците да оценят по-добре броя на простите числа в по-кратки интервали, например.
Но истинското значение се крие в ходовете, които са позволили на Гът и Мейнард да преодолеят бариерата - нови инструменти, които могат да се приложат и извън теорията на простите числа, посочва Радзивил. Той предполага, че новите стратегии могат да помогнат за опростяването на някои от предишните му работи по динамични системи, а също така могат да помогнат и при друго отдавнашно предположение, известно като проблема на Кейкея (Kakeya problem), при който преместваща се игла се върти на 360°, очертавайки сложни кръгли или делтовидни форми, като същевременно покрива възможно най-малка площ. Междувременно Гът е най-доволен от използването на тези идеи за изследване на дълбоката връзка между физиката на вълните и разпределението на множествата от числа.
Поглеждайки назад, Гът си спомня един цитат от австрийския поет Райнер Мария Рилке, който напътства начинаещия поет да "живее с въпросите", вместо да търси отговори. За Гът тази стратегия да се чувстваш удобно и неудобно от неразрешими проблеми резонира с опита му като математик.
"Изобщо не очаквам да разреша хипотезата на Риман", обяснява той. "Но се надяваме, че като се чудим за нещо, което не разбираме, ще намерим нещо, което е красиво или може би дори полезно."
Източник: ‘Sensational breakthrough’ marks step toward revealing hidden structure of prime numbers, Zack Savitsky, Science
Още по темата
Математика
Някои пробиви в най-трудната задача в теорията на числата. "Периодични таблици" на простите числа
Математика
Пробивът в теорията за простите числа показва, че простите числа могат да бъдат предвидени
Физика
Изненадващ скрит ред обединява простите числа и квазикристалите
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари