
Крайната цел на физиката е да опише възможно най-точно как точно ще се държи всяка физическа система, която може да съществува в нашата вселена. Законите на физиката трябва да се прилагат навсякъде: едни и същи правила трябва да работят за всички частици и полета на всички места и по всяко време.
Те трябва да са достатъчно добри, така че, независимо от съществуващите условия или провежданите експерименти, нашите теоретични прогнози да са в съответствие с измерените резултати. А наличието на изрична предсказваща сила означава, че ако знаете първоначалните условия на вашата система и законите, които я управляват, може да предвидите какви винаги ще бъдат резултатите - или относителната вероятност за набор от възможни резултати, обяснява в статия астрофизикът и научен журналист Итън Сийгъл (Ethan Siegel).
Най-успешните физически теории са:
- квантова теория на полето, описваща всяко от основните взаимодействия между частиците,
- както и Общата теория на относителността, която описва пространство-времето и гравитацията.
И все пак има една фундаментална симетрия, която се прилага не само за всички тези физични закони, но и за всички физически явления: CPT симетрия. И от почти 70 години учените познават теорема, която забранява нарушаването й.

В азбуката има много букви, които се отличават с особена симетрия. Обърнете внимание, че показаните тук главни букви имат една-единствена линия на симетрия; букви като "H", "I", "O" и "X" имат повече от една. Тази "огледална" симетрия, известна като паритет (или Р-симетрия), е потвърдена като валидна за всички силни, електромагнитни и гравитационни взаимодействия, където и да е тествана. Слабите взаимодействия обаче предлагат възможност за нарушаване на четността. Откриването и потвърждаването на това обстоятелство струва Нобеловата награда за физика за 1957 г. Кредит: math-only-math.com
За повечето от нас, когато чуят думата симетрия, се сещат за отразяването на нещата в огледало. Някои от буквите на нашата азбука проявяват този вид симетрия: "А" и "Т" са вертикално симетрични, а "B" и "Е" са хоризонтално симетрични. Буквата "О" е симетрична по отношение на всяка права линия, която минава през централната ѝ точка, както и притежава ротационна симетрия: независимо от начина, по който я завъртите, външният ѝ вид остава непроменен. Тези симетрии, известни съответно като симетрия на линиите и симетрия на точките, са двете симетрии, с които имаме най-голям опит в ежедневието си.
Но в природата се срещат и други видове симетрия. Ако имате хоризонтална линия и я преместите с каквато и да е стойност в хоризонталната линия, тя остава непроменена: все още е същата хоризонтална линия. Това е пример за това, което наричаме "транслационна" симетрия. Ако се намирате във вагон на влак и експериментите, които извършвате, дават един и същ резултат, независимо дали влакът е в покой или се движи бързо по релсите, това е симетрия при "ускоренията" (или трансформации на скоростта). Някои от тези общи симетрии винаги са валидни при известните физични закони, докато други са валидни само понякога: стига да са изпълнени определени условия.
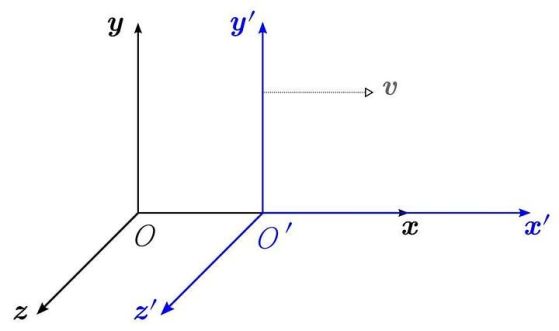 Ако една теория не е релативистично инвариантна, различните отправни системи, включително различните позиции и движения, ще възприемат различни закони на физиката (и ще се разминават с реалността). Фактът, че имаме симетрия при "ускоренията" или трансформациите на скоростта, ни подсказва, че имаме запазена величина: линеен импулс. Фактът, че една теория е инвариантна при всякакъв вид координатни или скоростни трансформации, е известен като инвариантност на Лоренц, а всяка инвариантна симетрия на Лоренц запазва симетрията на CPT. Въпреки това С, Р и Т (както и комбинациите СР, СТ и РТ) могат да бъдат нарушени поотделно. Кредит: Krea/Wikimedia Commons
Ако една теория не е релативистично инвариантна, различните отправни системи, включително различните позиции и движения, ще възприемат различни закони на физиката (и ще се разминават с реалността). Фактът, че имаме симетрия при "ускоренията" или трансформациите на скоростта, ни подсказва, че имаме запазена величина: линеен импулс. Фактът, че една теория е инвариантна при всякакъв вид координатни или скоростни трансформации, е известен като инвариантност на Лоренц, а всяка инвариантна симетрия на Лоренц запазва симетрията на CPT. Въпреки това С, Р и Т (както и комбинациите СР, СТ и РТ) могат да бъдат нарушени поотделно. Кредит: Krea/Wikimedia Commons
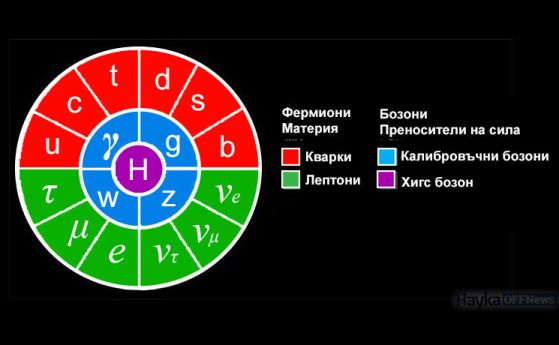
Ако искаме да слезем на фундаментално ниво и да разгледаме най-малките неделими частици, които съставляват всичко, което познаваме в нашата Вселена, това би ни накарало да разгледаме частиците от Стандартния модел. Състоящи се от фермиони (кварки и лептони) и бозони (глуони, фотон, W- и Z-бозони и Хигс), те обхващат всички известни ни частици, от които се състоят материята и лъченията, върху които пряко сме провеждали експерименти във Вселената. (Въпреки че има доказателства за съществуването на тъмната материя и тъмната енергия, те не са включени в тази картина и не могат да бъдат обяснени с нито една от известните частици от Стандартния модел).
Съгласно законите на Квантовата теория на полето и Общата теория на относителността можем да изчислим силите между всякакви частици във всяка конфигурация и да определим как те ще се движат, взаимодействат и развиват във времето. Можем да наблюдаваме как частиците на материята се държат при едни и същи условия с частиците на антиматерията и да определим къде поведението им е идентично едно с друго и къде се различава едно от друго. Можем да провеждаме експерименти, които са огледални аналози на други експерименти, и да отбелязваме резултатите. И в трите случая се проверява валидността на различни симетрии.
 Частиците и античастиците на Стандартния модел се подчиняват на всички видове закони за запазване, но има малки разлики в поведението на някои двойки частици/античастици, които могат да бъдат намек за произхода на бариогенезата. Кварките и лептоните са примери за фермиони, докато бозоните (долният ред) опосредстват силите и възникват като следствие от произхода на масата. Кредит: E. Siegel/Beyond the Galaxy
Частиците и античастиците на Стандартния модел се подчиняват на всички видове закони за запазване, но има малки разлики в поведението на някои двойки частици/античастици, които могат да бъдат намек за произхода на бариогенезата. Кварките и лептоните са примери за фермиони, докато бозоните (долният ред) опосредстват силите и възникват като следствие от произхода на масата. Кредит: E. Siegel/Beyond the Galaxy
Във физиката тези три фундаментални симетрии - симетрията между материята и антиматерията, симетрията между системите от частици и техните огледални отражения и симетрията на движението на часовника напред или назад - имат специфични имена и правила, които следват.
Зарядова симетрия (С): тази симетрия включва замяната на всяка частица в една система с нейния аналог от антиматерия. Нарича се зарядова симетрия, защото всяка заредена частица има противоположен заряд (например електрически или цветови) за съответната си античастица.
Пространствена инверсия (отражение), паритет (P): тази симетрия включва замяната на всяка частица, взаимодействие и разпад с нейния огледален аналог.
Симетрия на обръщане на времето (Т): тази симетрия налага физичните закони, засягащи взаимодействията на частиците, да се държат по абсолютно един и същ начин, независимо дали времето се движи напред или назад във времето.
Повечето от силите и взаимодействията, с които сме свикнали, се подчиняват независимо на всяка от тези три симетрии.
Ако хвърлим топка в гравитационното поле на Земята и нейната траектория на полета придобие форма като парабола, няма да има значение, ако замените частиците с античастици (C), няма да има значение, ако отразите вашата парабола в огледало или не (P), и няма значение дали сте преместили часовника напред или назад (Т), при условие че пренебрегнем неща като въздушно съпротивление и всякакви (не съвсем еластични) удари на земята.
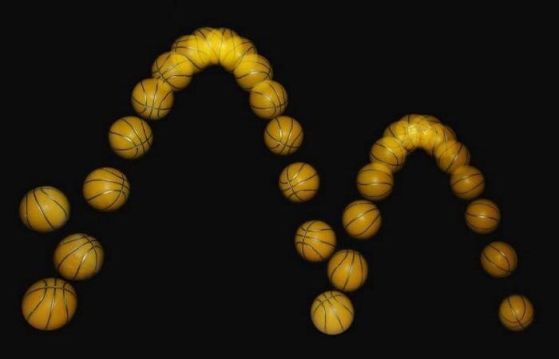
Топка в средата на отскок има своите минали и бъдещи траектории, определени от законите на физиката, но времето за нас ще тече само в бъдещето. Ако нямаше въздушно съпротивление и загуба на енергия всеки път, когато топката удари земята, наблюдателят не би могъл да разбере дали топката е започнала отляво и се е преместила надясно с течение на времето, или обратното. Докато законите на движението на Нютон са едни и същи, независимо дали часовниците се движат напред или назад във времето, и са симетрични по отношение ляво-дясно и материя-антиматерия, не всички закони на физиката се държат еднакво във всички тези симетрии.
Но отделните частици не се подчиняват на всички тези симетрии при всички физически условия, които можем да си представим. Наблюдавано е, че някои частици се държат фундаментално различно от техните античастици, нарушавайки C-симетрията.
Неутрино и антинеутрино - поне тези, които могат да се наблюдават - винаги се наблюдават в движение и се движат със скорост, близка до скоростта на светлината. Въпреки това, ако насочите левия си палец в посоката, в която се движат частиците, неутриното винаги се „върти“ в посоката, в която пръстите на лявата ви стискат около траекторията на неутриното, докато антинеутрино винаги са „десни“ по същия начин.
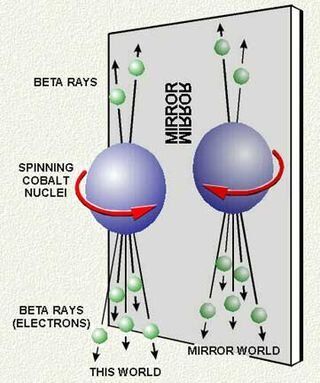 |
Кълбото вляво представя голям брой кобалтови ядра, всички с еднакъв спин и всички излъчващи бета-лъчи. От дясно е огледалният образ на същия процес. Посоката на спина е обърната, а посоката, в която се отделят най-много бета-лъчи, остава непроменена. Огледалният свят се различава от реалния свят. Р-четността се нарушава. Пространствената инверсия (отражението) променя света така, че той не е идентичен с реалния свят. Кредит: physics.nist.gov |
Ако една нестабилна частица, която има определен спин и след това се разпада, нейните разпадни продукти могат да имат същия спин или противоположен. Ако една нестабилна частица проявява предпочитан спин на своя разпад, тогава огледалният разпад ще има противоположен спин, нарушавайки P-симетрията.
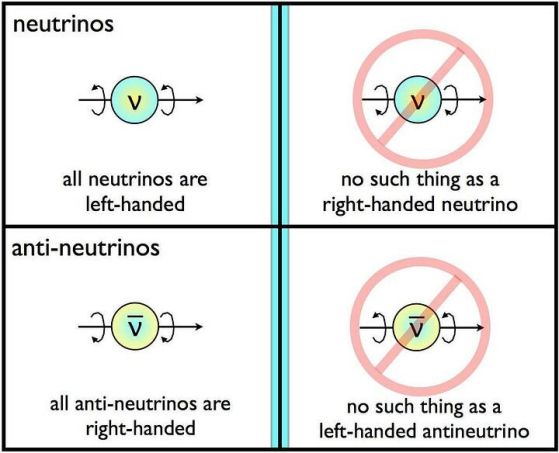
Природата не е симетрична между частици/античастици или между огледалните изображения на частиците. Или както симетрията на огледалното отражение, така и зарядовата симетрия се комбинират. До откриването на неутрино, които ясно нарушават огледалната симетрия дори без разпад, те бяха единствения потенциален начин за откриване на нарушения на P-симетрията. Кредит: E. Siegel/Beyond the Galaxy
Може да проверим комбинацията от тези симетрии, създавайки огледален образ на системата и след това заменим частиците в огледалото с античастици. Тази комбинация, която може да бъде нарушена или запазена, е известна като CP симетрия.
През 50-те и 60-те години на миналия век са проведени редица експерименти, които тестват всяка от тези симетрии и колко добре работят при гравитационни, електромагнитни, силни и слаби ядрени сили. При силно ядрено взаимодействие, както и при електромагнитно и гравитационно взаимодействие не се наблюдава нарушаване на симетрията. Това остава вярно дори и днес.
Може би изненадващо, слабите взаимодействия нарушават всяка от симетриите C, P и T поотделно, както и комбинации от всеки две такива симетрии (CP, PT и CT) заедно.
Тези смущения са важни за нашето разбиране за Вселената. Но всички фундаментални взаимодействия, всяко поотделно, винаги са обект на комбинация от всичките три от тези симетрии заедно: CPT симетрии (CPT инвариантност).

Нормалният мезон има спин (върти се) обратно на часовниковата стрелка около своя N полюс и след това се разпада с изпускане на електрон към своя N полюса. Прилагането на C-симетрия заменя частиците с античастици, което означава, че трябва да имаме антимезон, въртящ се обратно на часовниковата стрелка около своя разпад на Северния полюс, излъчвайки позитрон в северна посока. По същия начин P-симетрията обръща това, което виждаме в огледалото. Ако частиците и античастиците се държат различно при C-, P- или CP-симетрии, се казва, че тази симетрия е нарушена. Засега само слабото взаимодействие нарушава някое от трите, но е възможно да има нарушения в други сектори под текущите прагове. CPT обаче никога не е бил нарушаван едновременно. Кредит: E. Siegel/Beyond the Galaxy
CPT симетрията гласи, че всяка физическа система от частици, която се движи напред във времето, ще се подчинява на същите закони като идентична физическа система от античастици, отразени в огледало, което се движи назад във времето. Това е наблюдаваната точна симетрия на природата на фундаментално ниво и тя трябва да се спазва за всички физически явления, дори за тези, които тепърва ще бъдат открити.
Експерименти във физиката на елементарните частици се провеждат от десетилетия, за да се търсят нарушения на CPT симетрията. С много по-голяма точност от 1 част на 10 милиарда се наблюдава добра CPT симетрия в мезонни (кварк-антикварк), барионни (протон-антипротон) и лептонни (електрон-позитрон) системи. При нито един експеримент не е наблюдавано несъответствие с CPT симетрията, което е добре за Стандартния модел.
Това също е важно съображение от теоретична гледна точка, тъй като има CPT теорема, която изисква тази комбинация от симетрии, приложени заедно, да не се нарушава. Въпреки че това е доказано за първи път през 1951 г. от Джулиан Швингер (Julian Schwinger), има много изненадващи последици от факта, че CPT симетрията трябва да бъде запазена в нашата вселена, както и много проблеми, които биха се проявили, ако бъде фундаментално нарушена.

Можем да си представим, че има огледална вселена, където важат същите правила. Ако голямата червена частица, показана по-горе, е частица с импулс, ориентиран в една посока, и се разпада (белите стрелки) чрез силни, електромагнитни или слаби взаимодействия, създавайки „дъщерни“ частици в процеса, тогава това е същото като огледален процес на неговата античастица с обратен импулс (т.е. движение назад във времето). Ако огледалното отражение и за трите (C, P и T) симетрии се държи по същия начин като частица в нашата Вселена, тогава CPT симетрията се запазва.
Първото заключение е, че нашата вселена, каквато я познаваме, ще бъде неразличима от конкретна инкарнация на антивселената. Ако промените:
- позицията на всяка частица в позиция, която съответства на отражението с център на симетрия спрямо точка (P-трансформация),
- всяка частица се заменя със своя аналог антиматерия (C-трансформация),
- и импулса на всяка частица, обърнат със същата стойност и в обратна посока от сегашната й стойност (T- трансформация),
тогава тази антивселена ще се развива според точно същите физически закони като нашата собствена вселена.
Друго следствие е, че ако комбинацията от СРТ е в сила, то всяко нарушение на една от тях (С, Р или Т) трябва да съответства на еквивалентно нарушение на другите две комбинирани (съответно РТ, СТ или СР), за да се запази комбинацията от СРТ.
Ето защо учените знаят, че T-нарушението трябва да се появи в определени системи десетилетия, преди да могат да го измерят директно: защото наблюдаваното нарушение на СР изисква това да е така. Това означава също, че веднага щом се измери С-нарушение и Р-нарушение, веднага се разбира, че ще трябва да се нарушат и РТ-симетрията и СТ-симетрията.
 |
Стандартният модел прогнозира, че електрическият диполен момент на неутрона ще бъде десет милиарда пъти по-голям от границите на наблюдение. Единственото обяснение е, че нещо извън Стандартния модел по някакъв начин защитава тази CP симетрия при силни взаимодействия. Ако C е нарушено, PT също е нарушено; ако P е счупено, тогава и CT също; ако Т е нарушено, тогава и СР. Кредит: Andreas Knecht/public domain |
Но най-важното следствие от CPT теоремата е много дълбоката връзка между теорията на относителността и квантовата физика: инвариантността на Лоренц. Ако CPT симетрията е валидна симетрия, тогава симетрията на Лоренц, която гласи, че законите на физиката остават същите за наблюдателите във всички инерционни (т.е. неускоряващи се) референтни системи, също трябва да бъде валидна симетрия. Обратното обаче също е вярно, което означава, че ако нарушите CPT симетрията, тогава симетрията на Лоренц също е нарушена.
Поради редица причини това е не само лошо, но и потенциално катастрофално: разрушаването на основата, върху която е изградена съвременната физика.
Нарушаването на симетрията на Лоренц може да е модерно в някои области на теоретичната физика, особено в някои подходи към квантовата гравитация, но експерименталните ограничения за това са изключително силни.
В продължение на повече от 100 години са проведени много експериментални търсения за нарушения на инвариантността на Лоренц и резултатите в по-голямата част от случаите са отрицателни и надеждни. Ако законите на физиката са еднакви за всички наблюдатели, тогава CPT трябва да е валидна симетрия. А ако не е, то начините, по които се нарушава са миниатюрни, незабележими и изключително силно ограничени.

Квантовата гравитация се опитва да съчетае Общата теория на относителността на Айнщайн с квантовата механика. Квантовите корекции на класическата гравитация се визуализират като контурни диаграми, както е показано тук в бяло. Ако разширим Стандартния модел, за да включим гравитацията, симетрията, която описва CPT (симетрия на Лоренц), може да стане само приблизителна симетрия, която може да бъде нарушена. Подобни експериментални нарушения обаче досега не са наблюдавани. Кредит: SLAC National Accelerator Laboratory
Във физиката трябва да сме готови да поставим под съмнение нашите предположения и да изследваме всички възможности, без значение колко малко вероятни изглеждат или доколко противоречат на интуитивното ни разбиране за това как трябва да се държи природата. Но по подразбиране трябва да приемем, че законите на физиката, които са издържали всички експериментални тестове, представляват последователна теоретична основа и точно описват нашата реалност, трябва да се третират така, сякаш са правилни, докато не се докаже противното.
В този случай това означава, че предположението, че законите на физиката са еднакви навсякъде и за всички наблюдатели, трябва да се счита за валидно до доказване на противното.
Понякога частиците се държат различно от античастиците и това е добре. Понякога физическите системи се държат различно от техните огледални образи и това също е добре.
И понякога физическите системи се държат различно в зависимост от това дали времето върви напред или назад, което също е валидно. Трябва обаче да изискваме същото поведение да се наблюдава за:
- частици, движещи се напред във времето
- като за античастици, отразени в огледало, движещо се назад във времето;
Това е следствие от CPT теоремата. Това е единствената симетрия, стига физическите закони, за които знаем, да са верни, която трябва да бъде наистина ненарушима в нашата вселена.
Източник: The Universe’s most unbreakable symmetry, Starts With A Bang, Ethan Siegel



















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?
Nikor
На 30 септември 1928 е открит пеницилинът
Прост Човек
Ново обяснение за гигантските експлодиращи кратери в Сибир