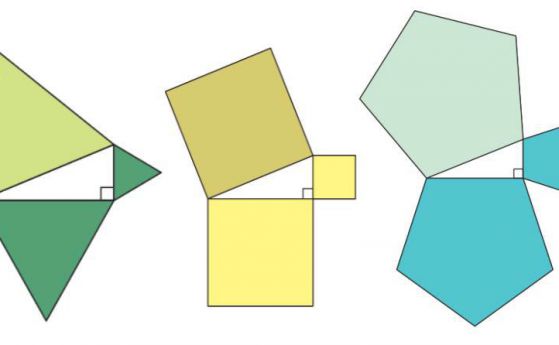
Имало едно време, в едно далечно, далечно царство, богат земевладелец, който решил да продаде част от нивата си. Това било преди около 4000 години, в днешния централен Ирак - и тази сделка със земя в крайна сметка ще доведе до пълна промяна в начина, по който разбираме историята на математиката.
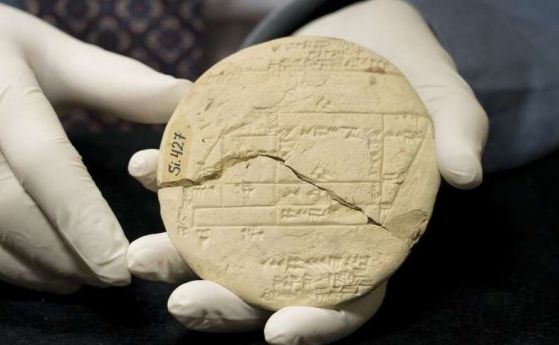
Ново изследване, публикувано тази седмица в списание Foundations of Science, предполага, че Si.427 - малка, непретенциозна глинена плочка, престояла в музей в Истанбул през последните 100 години - всъщност е най-старият известен пример за приложна геометрия в света. Нещо повече, тази плочка разкрива още нещо необикновено: вдъхновението и методологията, които са позволили на древните вавилонски математици да изпреварят Питагор с известната му теорема с няколко хилядолетия.
„Всяка книга по история ще ви каже, че тригонометрията започва от древногръцките астрономи“, разказва пред IFLScience авторът Даниел Мансфийлд (Daniel Mansfield).
„Обичам да мисля за вавилонското прозрение като за неочаквана предистория, която наистина е независима, тъй като вавилонците не са го използвали за измерване на звездите, а за измерване на земята“.
Преди четири години Мансфийлд създава сензация, когато той и неговият колега Норман Уайлдбергер (Norman Wildberger) стават първите, които декодират древна глинена плоча, известна като Plimpton 322. Този почти 4000-годишен артефакт е покрит с щателно организирани групи от числа, известни на съвременните математици като Питагорови тройки - тоест цели числа, които отговарят на теоремата на Питагор, като (3, 4, 5) или (5, 12, 13).
Мансфийлд и Уайлдбъргър разбират, че Plimpton 322 е тригонометрична таблица - един вид древен справочник за решаване на геометрични задачи. Но защо древните вавилонци са имали нужда от нещо подобно?
Тук идва новото изследване на Мансфийлд. Si.427 не е просто някаква абстрактна математическа задача - това е 4 000-годишен правен документ, отбелязва изследователят.
„Това е единственият известен пример за кадастрален документ от периода OB [Old Bablylon - Старият Вавилон], който представлява план, използван от геодезистите за определяне на границите на парцела“, обяснява Мансфийлд. "В този случай той ни разказва правни и геометрични подробности за нива, която е разделена, след като част от нея е продадена".
Отпред виждаме схема на нивата. Полето се разделя, а част от него се продава. Линиите очертават границите на различните парцели. Кредит: UNSW Sydney
Изненадващо е, но Si.427 предшества Plimpton 322 - ако случаят е такъв, това откритие е не само най-старият известен пример за геометрия в света, но и важна улика за употребата на вавилонската математика.
„Вавилонската [математика] ... е била много сложна за своето време“, коментира Мансфийлд пред IFLScience, „и сега знаем, че те са използвали това разбиране за решаване на съвременни проблеми свързани със собствеността върху земята и границите ... Сега, когато знаем с какви проблеми са се сблъскали, други глинени таблици започват да придобиват повече смисъл".
Това е важно, защото стандартната история на тригонометрията е, че тя е изобретена от древногръцки астрономи за изучаване на нощното небе. Si.427 преобръща тази теория. Тригонометрията - или както я нарича Мансфийлд, „прототригонометрията“ - е разработена независимо от вавилонците хиляди години по-рано и нейното вдъхновение е безпогрешно земно.
„С тази нова глинена таблица всъщност за първи път можем да видим защо се интересуват от геометрията [древните вавилонци]: за да определят точните граници на земята су“, обяснява Мансфийлд. „Това е от период, в който земята започва да става частна - хората започват да мислят за земята като „моята земя и вашата земя“, като искат да установят подходящи граници, за да имат положителни съседски отношения. И точно това казва тази таблица. Това е нива, която се разделя и се създават нови граници".
На гърба на таблицята има текст, написан с клинопис, една от най-ранните системи за писане. Текстът съответства на схемата отпред - описва размера на нивата. Кредит: UNSW Sydney
Но вавилонците не просто „изпреварват“ гърците, обяснява Мансфийлд - тази „прототригонометрия“ има съвсем различна гледна точка. Няма степени или функции като sin или cos. Всъщност от съвременна гледна точка задачите, решени от таблици като Si.427 и Plimpton 322, изглеждат почти напълно обратни: докато днешните ученици по математика са свикнали със задачи, които задават дължините на страните на правоъгълен триъгълник, вавилонските математици и геодезисти вместо това да били фокусирани върху това кой набор от дължини на страните ще доведе до хубава двойка перпендикулярни линии.
„Забавно е, защото този подход към геометрията е напълно неочакван“, коментира Мансфийлд. „Това е далеч извън нашата математическа култура. Така че тя ни изглежда нова и свежа, въпреки че е на почти 4000 години”.
Таблицата може да е на около четири хилядолетия, но това не означава, че не може да ни научи на нищо - и Мансфийлд вярва, че този древен начин на математика може да има някои важни съвременни приложения.
„Древната математика не е толкова сложна, колкото съвременната математика. Но понякога търсим прости отговори вместо сложни“, отбелязва Мансфийлд. „И не говоря само за това как учениците по математика искат да бъдат изпитите им. Предимството на простия подход е, че е бърз ... [може] да бъде от полза в компютърната графика или всяко приложение, където скоростта е по-важна от прецизността".
Справка: Mansfield, D.F. Plimpton 322: A Study of Rectangles. Found Sci (2021). https://doi.org/10.1007/s10699-021-09806-0
Източник: This Ancient Tablet Secretly Held The Oldest Evidence Of Applied Geometry In The World, IFLScience
Още по темата
Математика
Реална ли е математиката? Дали древните са възприемали математиката като нас?
Математика
Първата тригонометрична таблица от Вавилон е по-лесна от съвременните (видео)
Математика
Първото предсказано от човек слънчево затъмнение се случва на 28 май 585 година пр. н.е.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари