Да се изчисли броя на възможните конфигурации, които могат да заемат много топки в ограничен обем е задача, за която на математиците им трябва компютър по-голям от Вселената.
Но физици от Университета Кеймбридж са намерили начин, използвайки "ентропията" на такива системи.
Работата е публикувана в списание Physical Review E.
Колко начина има да се подредят 128 топки? Намирането на отговора е по-трудно, отколкото си мислите, а решаването на тази задача може да доразвие теорията на земната механика за несвързани почви или т.нар. *насипни тела. На практика тази задача засяга поведението на пясък (дюни), почва, зърно, сняг (лавини), пише NewScientist.
*Насипен материал е механична система, която се състои от голям брой отделни твърди частици, толкова много, че свойствата на системата се определя преди всичко от характеристиките на взаимодействието между отделните частици, които могат да бъдат извлечени от свойствата на отделните частици. Частиците също така трябва да са достатъчно големи (макроскопични), че да може да се пренебрегне движението на съставящите ги единични молекули. Знаейки характеристиките на взаимодействието между съставните частици, може да се прогнозира какви свойства в крайна сметка ще има цялата система. Тези материали се изучават от земната механика за несвързани почви - пясък, чакъл, други несвързани почви и сняг, пример могат да бъдат 10 000 зелки или астероиди.
Примери за насипни материали. Източник: Wikipedia.
Математиците отдавна се интересуват от най-ефективният начин да се опаковат сфери. Ако ги хвърлим в кутия и ги разклатим хубаво докато застанат на място, има множество възможни начини това да стане - толкова много, че според изследователите за преброяването им ще трябва компютър по-голям от Вселената.
Най-важното свойство на една насипна система от тела е как нейните съставни частици се разпределят в пространството. Математически методи, като например преките изчисления, не позволяват да се изчисли броя на начините на разпределение на частицитете за системи, които се състоят от повече от 20 частици. Дори най-мощните компютри не могат да се справят с тази задача, поради огромното количество ресурси, които ще бъдат необходими в търсенето на всички възможни комбинации.
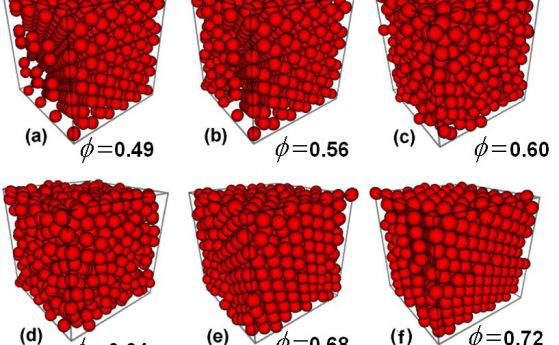
Но сега учените имат по-различен подход. Използвайки компютърно моделиране, те разглеждат система, състояща се от 128 сфери. Вместо да изчисляват всички възможни конфигурации, те взели определени термодинамични характеристики на системата, за да определят на тяхна основа конфигурационната й ентропия.
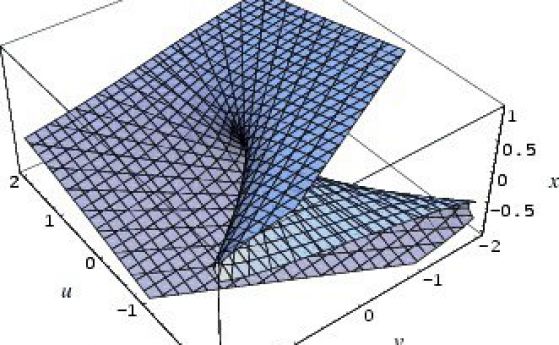
Представете си всяко от възможните положения на сферите като точка на огромен енергиен пейзаж. Когато топките се движат хлабаво, те имат повече енергия, което ги поставя в по-високо в енергийния ландшафт. Задръстеното състояние съответства на дъното на долина, където топките не могат да се придвижат на по-ниско енергийно състояние.
Изследователите взели предвид факта, че частиците имат склонност да заемат определени точки в пространствената конфигурация, които може да се разглеждат като точки на привличане (енергийни долини - атрактори). А цялата останала конфигурация зависи от разположението в тези области. Въз основа на това, учените са извели уравнение, което позволява само въз основа на средния обем на областите на привличане и общият обем на насипното тяло, да се оцени конфигурационната ентропия. Обемът на областите на привличане се изчислява чрез термодинамично интегриране.
Резултатите показват, че 128 частици са способни да се организират в около 10 250 различни конфигурации. Новият метод обаче позволява да се решават по-сложни задачи, при които броят на частиците е 50 милиона пъти повече. Това дава възможност да се изследва поведението на сложни системи като лавини, плаващи пясъци и дори някои приложения в областта на изкуствения интелект.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари