

–ö–Ψ―Ä–Β–Ι―¹–Κ–Η―è―² –Φ–Α―²–Β–Φ–Α―²–Η–Κ –ß–Η–Ϋ–Β–Ψ–Ϋ –ë–Α–Β–Κ (Jineon Baek) –Ψ―² ―É–Ϋ–Η–≤–Β―Ä―¹–Η―²–Β―²–Α –ô–Ψ–Ϋ―¹–Β–Ι –Β –Ω―Ä–Β–¥―¹―²–Α–≤–Η–Μ ―Ä–Β―à–Β–Ϋ–Η–Β –Ζ–Α –Ζ–Α–¥–Α―΅–Α―²–Α ―¹ –Ω―Ä–Β–Φ–Β―¹―²–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α –¥–Η–≤–Α–Ϋ –Ω―Ä–Β–Ζ ―²–Β―¹–Β–Ϋ L-–Ψ–±―Ä–Α–Ζ–Β–Ϋ –Κ–Ψ―Ä–Η–¥–Ψ―Ä.¬† –î–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Ψ―²–Ψ, –Κ–Ψ–Β―²–Ψ –Β –Ω–Ψ–≤–Β―΅–Β –Ψ―² 100 ―¹―²―Ä–Α–Ϋ–Η―Ü–Η, –Β –Ω―É–±–Μ–Η–Κ―É–≤–Α–Ϋ–Ψ –Ϋ–Α ―¹―ä―Ä–≤―ä―Ä–Α –Ζ–Α –Ω―Ä–Β–Ω―Ä–Η–Ϋ―²–Η arXiv.
–ü–Ψ―¹―²–Α–Ϋ–Ψ–≤–Κ–Α –Ϋ–Α –Ζ–Α–¥–Α―΅–Α―²–Α
–ü–Ψ–≤–Β―΅–Β―²–Ψ ―Ö–Ψ―Ä–Α, –Κ–Ψ–Η―²–Ψ ―¹–Α –Ω―Ä–Β–Φ–Β―¹―²–≤–Α–Μ–Η –Ω–Ψ–Κ―ä―â–Ϋ–Η–Ϋ–Α―²–Α ―¹–Η, ―¹–Α ―¹–Β ―¹–±–Μ―ä―¹–Κ–Α–Μ–Η ―¹ –Ω―Ä–Ψ–±–Μ–Β–Φ–Α ―¹ –Ω―Ä–Β–Ϋ–Α―¹―è–Ϋ–Β―²–Ψ –Ϋ–Α –¥–Η–≤–Α–Ϋ - –≤―ä–Ζ–Ϋ–Η–Κ–≤–Α, –Κ–Ψ–≥–Α―²–Ψ ―¹–Β –Ψ–Ω–Η―²–≤–Α―²–Β –¥–Α –Ω―Ä–Β–Ϋ–Β―¹–Β―²–Β –¥–Η–≤–Α–Ϋ –Ω―Ä–Β–Ζ ―΅―É–Ω–Β―â –Ω–Ψ–¥ –Ω―Ä–Α–≤ ―ä–≥―ä–Μ –Κ–Ψ―Ä–Η–¥–Ψ―Ä (–Ω―Ä–Β–¥―¹―²–Α–≤–Β―²–Β ―¹–Η ―¹―²―ä–Μ–±–Η―â–Ϋ–Α –Κ–Μ–Β―²–Κ–Α). –ö–Ψ–Ι –Β –Ϋ–Α–Ι-–≥–Ψ–Μ–Β–Φ–Η―è―² –¥–Η–≤–Α–Ϋ, –Κ–Ψ–Ι―²–Ψ –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ω―Ä–Β–Ϋ–Β―¹–Β –Ω―Ä–Β–Ζ –¥–Α–¥–Β–Ϋ ―ä–≥―ä–Μ, –±–Β–Ζ –¥–Α ―¹–Β –Ζ–Α–Κ–Μ–Β―â–Η? –Δ–Α–Ζ–Η –Ζ–Α–¥–Α―΅–Α –Β –Ω–Ψ―¹―²–Α–≤–Β–Ϋ–Α –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η –Ψ―² –Κ–Α–Ϋ–Α–¥―¹–Κ–Η―è –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α –¦–Β–Ψ –€–Ψ–Ζ–Β―Ä –Ω―Ä–Β–Ζ 1966 –≥. –Η –¥–Ψ―¹–Β–≥–Α –Ψ―¹―²–Α–≤–Α –Ϋ–Β―Ä–Β―à–Β–Ϋ–Α.
–ü―ä―Ä–≤–Ψ–Ϋ–Α―΅–Α–Μ–Ϋ–Ψ –€–Ψ–Ζ–Β―Ä ―¹–Β ―³–Ψ–Κ―É―¹–Η―Ä–Α –≤―ä―Ä―Ö―É –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Ψ―¹―²―²–Α –¥–Α ―¹–Β ―Ä–Α–Ζ―Ä–Α–±–Ψ―²–Η –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Ψ, –Ω–Ψ–Κ–Α–Ζ–≤–Α―â–Ψ –Κ–Α–Κ –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α―²–Α –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α –Ζ–Α ―Ä–Β―à–Α–≤–Α–Ϋ–Β –Ϋ–Α ―²–Α–Κ―ä–≤ –Ω―Ä–Ψ–±–Μ–Β–Φ, ―¹ –Ω–Ψ–Φ–Ψ―â―²–Α –Ϋ–Α –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Α –¥–≤―É–Φ–Β―Ä–Ϋ–Α ―³–Ψ―Ä–Φ–Α, –¥–Ψ–Κ–Α―²–Ψ ―²―è ―¹–Β –¥–≤–Η–Ε–Η –Ψ–Κ–Ψ–Μ–Ψ –Ω―Ä–Α–≤ ―ä–≥―ä–Μ –Ϋ–Α –Ω―Ä–Α–Ζ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ (–Κ–Α―²–Ψ –Κ–Ψ―Ä–Η–¥–Ψ―Ä), –Κ–Ψ–Ι―²–Ψ –Η–Φ–Α –Β–¥–Η–Ϋ–Η―Ü–Α ―à–Η―Ä–Η–Ϋ–Α.
 |
–î–Η–≤–Α–Ϋ―ä―² –Ϋ–Α –î–Ε–Ψ–Ϋ –Ξ–Α–Φ―ä―Ä―¹–Μ–Η –Η–Φ–Α –Ω–Μ–Ψ―â 2.2074, –Ϋ–Ψ –Ϋ–Β –Β –Ϋ–Α–Ι-–≥–Ψ–Μ―è–Φ–Α―²–Α, –Η–Φ–Α –Ω–Ψ-–¥–Ψ–±―Ä–Ψ ―Ä–Β―à–Β–Ϋ–Η–Β. –ö―Ä–Β–¥–Η―²:¬†Wikimedia Commons¬† |
–Δ―ä―Ä―¹–Β–Ϋ–Β –Ϋ–Α ―Ä–Β―à–Β–Ϋ–Η–Β
–ë–Α–Β–Κ ―Ä–Α–±–Ψ―²–Η ―¹ –¥–Η–≤–Α–Ϋ ―¹ ―³–Ψ―Ä–Φ–Α "–≥―ä―Ä–≤―ä―Ä" (–Ϋ–Α–Ω–Ψ–¥–Ψ–±―è–≤–Α―â–Α ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α ―²–Β–Μ–Β―³–Ψ–Ϋ–Ϋ–Α ―¹–Μ―É―à–Α–Μ–Κ–Α) –Κ–Α―²–Ψ –¥–Β–Φ–Ψ–Ϋ―¹―²―Ä–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α ―³–Ψ―Ä–Φ–Α. –î–Η–≤–Α–Ϋ―ä―²¬† –Ϋ–Α –™―ä―Ä–≤―ä―Ä –Β –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Α –Κ–Ψ–Ϋ―¹―²―Ä―É–Κ―Ü–Η―è, ―Ä–Α–Ζ―Ä–Α–±–Ψ―²–Β–Ϋ–Α –Ψ―² –î–Ε–Ψ―É–Ζ–Β―³ –™–Β―Ä–≤―ä―Ä (Joseph Gerver), –Ω―Ä–Ψ―³–Β―¹–Ψ―Ä –≤ –Θ–Ϋ–Η–≤–Β―Ä―¹–Η―²–Β―²–Α –†―É―²–≥–Β―Ä―¹, –Ω―Ä–Β–Ζ 1992 –≥. –Δ–Ψ–≤–Α –Β –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Ψ –Κ―É–±–Ψ–Η–¥ ―¹ U-–Ψ–±―Ä–Α–Ζ–Ϋ–Α –Ω―Ä–Β–¥–Ϋ–Α ―΅–Α―¹―², –Ω–Μ–Ψ―¹―ä–Κ –≥―Ä―ä–± ―¹―ä―¹ –Ζ–Α–Ψ–±–Μ–Β–Ϋ–Η ―Ä―ä–±–Ψ–≤–Β –Η –Ω–Μ–Ψ―¹–Κ–Η, –Ψ–±―ä―Ä–Ϋ–Α―²–Η –Ϋ–Α–Ω―Ä–Β–¥ –Ψ–±–Μ–Β–≥–Α–Μ–Κ–Η. –ê–Κ–Ψ –≤–Η ―¹–Β ―¹―²―Ä―É–≤–Α ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α ―¹―²―Ä–Α–Ϋ–Ϋ–Α, ―²―Ä―è–±–≤–Α –¥–Α ―¹–Β –Ω–Ψ–¥―΅–Β―Ä―²–Α–Β, ―΅–Β –Φ–Α―²–Β–Φ–Α―²–Η―Ü–Η―²–Β ―²―ä―Ä―¹―è―² ―³–Ψ―Ä–Φ–Α―²–Α, –Κ–Ψ―è―²–Ψ ―â–Β –¥–Α–¥–Β –Φ–Α–Κ―¹–Η–Φ–Α–Μ–Ϋ–Α –Ω–Μ–Ψ―â –Η ―¹―ä―â–Β–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ ―â–Β –Φ–Ψ–Ε–Β –¥–Α –Φ–Η–Ϋ–Β –Ω―Ä–Β–Ζ ―ä–≥―ä–Μ–Α.
–ü–Ψ–Μ―É―΅–Β–Ϋ–Α―²–Α –Ψ–Ω―²–Η–Φ–Α–Μ–Ϋ–Α –Ω–Μ–Ψ―â –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α ―¹–Β –Ϋ–Α―Ä–Η―΅–Α –Κ–Ψ–Ϋ―¹―²–Α–Ϋ―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α. –Δ–Ψ―΅–Ϋ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ϋ–Α –Κ–Ψ–Ϋ―¹―²–Α–Ϋ―²–Α―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α –Β –Ψ―²–Κ―Ä–Η―² –Ω―Ä–Ψ–±–Μ–Β–Φ. –£–Ψ–¥–Β―â–Ψ―²–Ψ ―Ä–Β―à–Β–Ϋ–Η–Β –Ψ―² –î–Ε–Ψ―É–Ζ–Β―³ –™―ä―Ä–≤―ä―Ä –Η–Φ–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ω―Ä–Η–±–Μ–Η–Ζ–Η―²–Β–Μ–Ϋ–Ψ 2,2195.
 –î–Η–≤–Α–Ϋ―ä―² –Ϋ–Α –™―ä―Ä–≤―ä―Ä ―¹ –Ω–Μ–Ψ―â 2.2195 ―¹ 18 –Κ―Ä―ä–≥–Ψ–≤–Η ―¹–Β–≥–Φ–Β–Ϋ―²–Α. –ö―Ä–Β–¥–Η―²: Wikimedia Commons¬†
–î–Η–≤–Α–Ϋ―ä―² –Ϋ–Α –™―ä―Ä–≤―ä―Ä ―¹ –Ω–Μ–Ψ―â 2.2195 ―¹ 18 –Κ―Ä―ä–≥–Ψ–≤–Η ―¹–Β–≥–Φ–Β–Ϋ―²–Α. –ö―Ä–Β–¥–Η―²: Wikimedia Commons¬†
–ë–Α–Β–Κ –Ω―Ä–Η–Μ–Α–≥–Α –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η –Η–Ϋ―¹―²―Ä―É–Φ–Β–Ϋ―²–Η, –Ζ–Α –¥–Α –Ω―Ä–Β–Φ–Η–Ϋ–Β –Ω―Ä–Β–Ζ –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Ψ―²–Ψ, ―΅–Β ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α –™―ä―Ä–≤―ä―Ä –Β –Ψ–Ω―²–Η–Φ–Α–Μ–Ϋ–Α, ―¹―²―ä–Ω–Κ–Α –Ω–Ψ ―¹―²―ä–Ω–Κ–Α, –Ω―Ä–Β–¥–Η –≤ –Κ―Ä–Α–Ι–Ϋ–Α ―¹–Φ–Β―²–Κ–Α –¥–Α ―¹―²–Η–≥–Ϋ–Β –¥–Ψ –Ψ―²–≥–Ψ–≤–Ψ―Ä–Α: –½–Α –Κ–Ψ―Ä–Η–¥–Ψ―Ä ―¹ ―à–Η―Ä–Η–Ϋ–Α 1 –Β–¥–Η–Ϋ–Η―Ü–Α –Φ–Α–Κ―¹–Η–Φ–Α–Μ–Ϋ–Α―²–Α –Ω–Μ–Ψ―â –Ϋ–Α –¥–Η–≤–Α–Ϋ –Ϋ–Α –™―ä―Ä–≤―ä―Ä –Φ–Ψ–Ε–Β –¥–Α –±―ä–¥–Β ―¹–Α–Φ–Ψ 2,2195 –Β–¥–Η–Ϋ–Η―Ü–Η.
 –î–≤–Η–Ε–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α¬†–Ω―Ä–Β–Φ–Β―¹―²–≤–Α―⬆―¹–Β –¥–Η–≤–Α–Ϋ –≤ –Ω–Β―Ä―¹–Ω–Β–Κ―²–Η–≤–Α―²–Α –Ϋ–Α –Κ–Ψ―Ä–Η–¥–Ψ―Ä–Α (–Ψ―²–≥–Ψ―Ä–Β) –Η –¥–Η–≤–Α–Ϋ–Α (–Ψ―²–¥–Ψ–Μ―É). –ö―Ä–Β–¥–Η―²: arXiv (2024). DOI: 10.48550/arxiv.2411.19826
–î–≤–Η–Ε–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α¬†–Ω―Ä–Β–Φ–Β―¹―²–≤–Α―⬆―¹–Β –¥–Η–≤–Α–Ϋ –≤ –Ω–Β―Ä―¹–Ω–Β–Κ―²–Η–≤–Α―²–Α –Ϋ–Α –Κ–Ψ―Ä–Η–¥–Ψ―Ä–Α (–Ψ―²–≥–Ψ―Ä–Β) –Η –¥–Η–≤–Α–Ϋ–Α (–Ψ―²–¥–Ψ–Μ―É). –ö―Ä–Β–¥–Η―²: arXiv (2024). DOI: 10.48550/arxiv.2411.19826
–ö–Α―²–Ψ ―΅–Α―¹―² –Ψ―² –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Ψ―²–Ψ, –ë–Α–Β–Κ ―¹―ä―â–Ψ ―²–Α–Κ–Α ―¹―²―Ä–Ψ–≥–Ψ –¥–Β―³–Η–Ϋ–Η―Ä–Α ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α –≥―ä―Ä–≤―ä―Ä, –Κ–Ψ–Ι―²–Ψ –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α. –ü–Ψ ―²–Ψ–Ζ–Η –Ϋ–Α―΅–Η–Ϋ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Η―²–Β –Η–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η–Η –Ϋ–Α ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α –±–Η―Ö–Α –¥–Ψ–≤–Β–Μ–Η –¥–Ψ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Η –Ψ―²–≥–Ψ–≤–Ψ―Ä–Η.
–Δ―ä–Ι –Κ–Α―²–Ψ ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ–Α –Β ―è―¹–Ϋ–Ψ –¥–Β―³–Η–Ϋ–Η―Ä–Α–Ϋ–Α –≤ ―¹–Α–Φ–Ψ―²–Ψ –Ϋ–Α―΅–Α–Μ–Ψ, –Ψ―²–≥–Ψ–≤–Ψ―Ä―ä―², –Κ–Ψ–Ι―²–Ψ –ë–Α–Β–Κ –Ϋ–Α–Φ–Η―Ä–Α, –±–Η –Φ–Ψ–≥―ä–Μ –¥–Α –±―ä–¥–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ϋ –≤ ―Ä–Β–Α–Μ–Ϋ–Η―è ―¹–≤―è―² –Ψ―² ―Ö–Ψ―Ä–Α, –Κ–Ψ–Η―²–Ψ ―¹–Β –Ψ–Ω–Η―²–≤–Α―² –¥–Α –Ω―Ä–Β–Φ–Β―¹―²―è―² –¥–Η–≤–Α–Ϋ–Α –Ω―Ä–Β–Ζ L-–Ψ–±―Ä–Α–Ζ–Β–Ϋ –Κ–Ψ―Ä–Η–¥–Ψ―Ä - –≤―ä–Ω―Ä–Β–Κ–Η ―΅–Β –±–Η ―²―Ä―è–±–≤–Α–Μ–Ψ –¥–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Α –Ϋ–Α ―¹―ä―â–Α―²–Α ―³–Ψ―Ä–Φ–Α –Ϋ–Α –¥–Η–≤–Α–Ϋ.
–î–≤–Ψ–Ι–Ϋ–Η―è―² –¥–Η–≤–Α–Ϋ –Ϋ–Α –†–Ψ–Φ–Η–Κ
–£–Α―Ä–Η–Α–Ϋ―² –Ϋ–Α –Ζ–Α–¥–Α―΅–Α―²–Α ―¹ –¥–Η–≤–Α–Ϋ–Α ―²―ä―Ä―¹–Η ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –Ϋ–Α–Ι-–≥–Ψ–Μ―è–Φ–Α―²–Α –Ω–Μ–Ψ―â, –Κ–Ψ―è―²–Ψ –Φ–Ψ–Ε–Β –¥–Α –Ζ–Α–Ψ–±–Η–Κ–Α–Μ―è –Κ–Α–Κ―²–Ψ –Μ–Β–≤–Η―è, ―²–Α–Κ–Α –Η –¥–Β―¹–Ϋ–Η―è 90-–≥―Ä–Α–¥―É―¹–Ψ–≤ ―ä–≥―ä–Μ –≤ –Κ–Ψ―Ä–Η–¥–Ψ―Ä ―¹ –Β–¥–Η–Ϋ–Η―΅–Ϋ–Α ―à–Η―Ä–Η–Ϋ–Α (–Κ―ä–¥–Β―²–Ψ –Μ–Β–≤–Η―è―² –Η –¥–Β―¹–Ϋ–Η―è―² ―ä–≥―ä–Μ ―¹–Α ―Ä–Α–Ζ–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η –¥–Ψ―¹―²–Α―²―ä―΅–Ϋ–Ψ –¥–Α–Μ–Β―΅ –Β–¥–Η–Ϋ –Ψ―² –¥―Ä―É–≥, ―²–Α–Κ–Α ―΅–Β –Β–¥–Η–Ϋ–Η―è―² –¥–Α –±―ä–¥–Β –Ϋ–Α–Ω―ä–Μ–Ϋ–Ψ –Ω―Ä–Β–Ψ–¥–Ψ–Μ―è–Ϋ –Ω―Ä–Β–¥–Η ―¹–Β ―¹―²–Η–≥–Ϋ–Β –¥―Ä―É–≥–Η―è). –î–Ψ–Μ–Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü–Α –Ϋ–Α –Ω–Μ–Ψ―â –Ω―Ä–Η–±–Μ–Η–Ζ–Η―²–Β–Μ–Ϋ–Ψ 1,64495521 –Β –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ―² –î–Α–Ϋ –†–Ψ–Φ–Η–Κ. 18-–Κ―Ä–Η–≤–Η ―¹–Β–Κ―Ü–Η–Η –Ψ–Ω–Η―¹–≤–Α―² –Ϋ–Β–≥–Ψ–≤–Η―è –¥–Η–≤–Α–Ϋ.
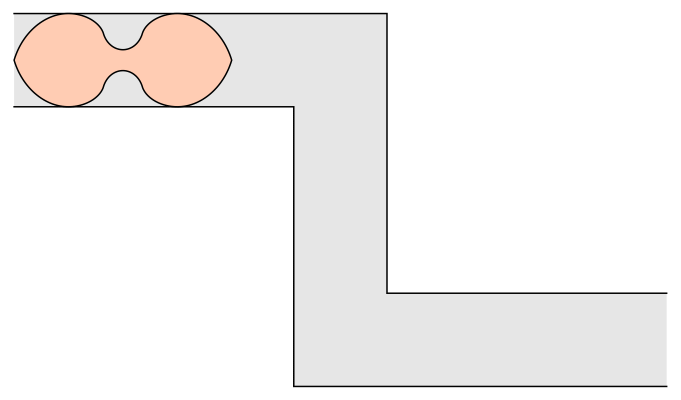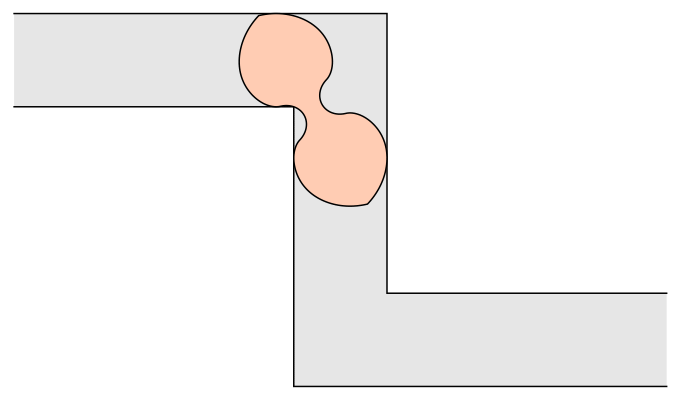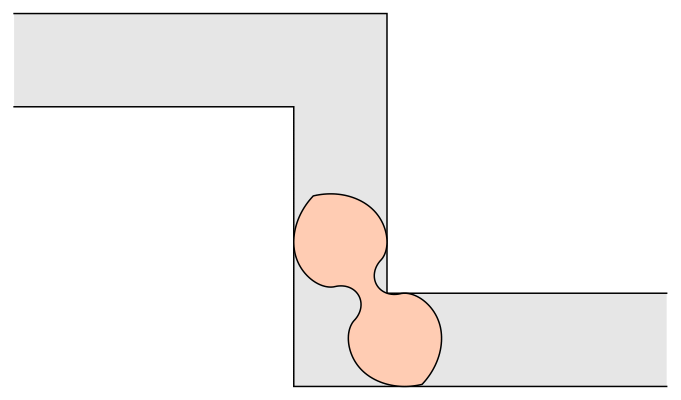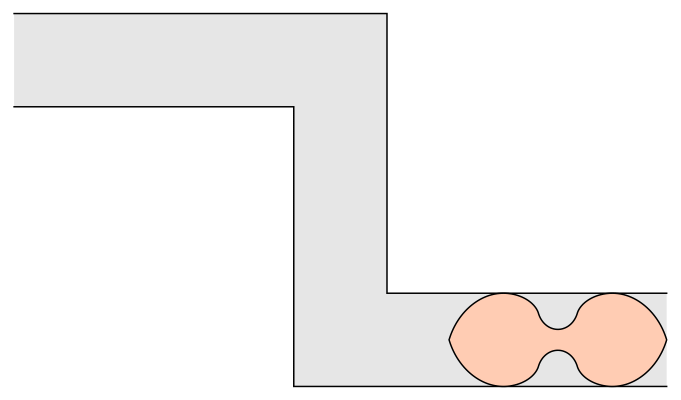 –î–Η–≤–Α–Ϋ –Ϋ–Α –†–Ψ–Φ–Η–Κ. –ö―Ä–Β–¥–Η―²: Wikimedia Commons
–î–Η–≤–Α–Ϋ –Ϋ–Α –†–Ψ–Φ–Η–Κ. –ö―Ä–Β–¥–Η―²: Wikimedia Commons
–ü―Ä–Β–¥―¹―²–Ψ–Η –Ω―Ä–Ψ–≤–Β―Ä–Κ–Α
–ö–Α–Κ―²–Ψ –Ω―Ä–Η –≤―¹–Η―΅–Κ–Η –Ω–Ψ–¥–Ψ–±–Ϋ–Η –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Α, ―²–Β–Ζ–Η –Ϋ–Α –ë–Α–Β–Κ ―â–Β ―²―Ä―è–±–≤–Α –¥–Α –±―ä–¥–Α―² –Ω–Ψ–¥–Μ–Ψ–Ε–Β–Ϋ–Η –Ϋ–Α –Ω―Ä–Ψ–≤–Β―Ä–Κ–Α –Ψ―² –¥―Ä―É–≥–Η –Φ–Α―²–Β–Φ–Α―²–Η―Ü–Η, –Ζ–Α –¥–Α ―¹–Β –≥–Α―Ä–Α–Ϋ―²–Η―Ä–Α, ―΅–Β –¥–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―¹―²–≤–Ψ―²–Ψ –Φ―É –Β –Ω―Ä–Α–≤–Η–Μ–Ϋ–Ψ –Η –¥–Β–Ι―¹―²–≤–Η―²–Β–Μ–Ϋ–Ψ –≤–Ψ–¥–Η –¥–Ψ –Ψ–Ω―²–Η–Φ–Α–Μ–Ϋ–Ψ―²–Ψ ―Ä–Β―à–Β–Ϋ–Η–Β –Ϋ–Α –¥–Α–¥–Β–Ϋ –Ω―Ä–Ψ–±–Μ–Β–Φ.
–Γ–Ω―Ä–Α–≤–Κ–Α: Jineon Baek, Optimality of Gerver's Sofa, arXiv (2024). DOI: 10.48550/arxiv.2411.19826
–‰–Ζ―²–Ψ―΅–Ϋ–Η―Ü–Η:
Mathematician solves the moving sofa problem, Bob Yirka, Phys.org
Moving sofa problem, wikipedia
–û―â–Β –Ω–Ψ ―²–Β–Φ–Α―²–Α

–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–€–Α―²–Β–Φ–Α―²–Η―Ü–Η –Ψ―²–Κ―Ä–Η–≤–Α―² –Ϋ–Ψ–≤ –Κ–Μ–Α―¹ ―³–Ψ―Ä–Φ–Η, –Κ–Ψ–Η―²–Ψ ―¹–Β ―¹―Ä–Β―â–Α―² –≤ –Ω―Ä–Η―Ä–Ψ–¥–Α―²–Α

–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–ï–Κ―¹–Ω–Β―Ä―²–Η –Ψ–±―¹―ä–Ε–¥–Α―² ―³–Η–Ζ–Η–Κ–Α―²–Α –Η –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α―²–Α –≤ ―¹–Β―Ä–Η–Α–Μ–Α "–½–Α–¥–Α―΅–Α―²–Α –Ζ–Α ―²―Ä–Η―²–Β ―²–Β–Μ–Α"
–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–€–Α―²–Β–Φ–Α―²–Η―Ü–Η ―Ä–Α–Ζ–Κ―Ä–Η–≤–Α―² ―³–Ψ―Ä–Φ–Η―²–Β –Ϋ–Α "–Φ–Β–Κ–Η―²–Β –Ω–Μ–Ψ―΅–Κ–Η" –≤ –Φ–Ψ–Ζ–Α–Ι–Κ–Α―²–Α –Ϋ–Α –Ε–Η–≤–Η―²–Β ―²―ä–Κ–Α–Ϋ–Η





















–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
–ù―è–Φ–Α –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η –Κ―ä–Φ ―²–Α–Ζ–Η –Ϋ–Ψ–≤–Η–Ϋ–Α !
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
4I4ATA
–ù–Ψ–≤, ―¹–Κ―Ä–Η―² –¥–Ψ―¹–Β–≥–Α –≤―Ö–Ψ–¥ –≤ –Ω–Η―Ä–Α–Φ–Η–¥–Α―²–Α –Ϋ–Α –€–Η–Κ–Β―Ä–Η–Ϋ –Β –Ψ―²–Κ―Ä–Η―² –Ω–Ψ –Α–Ϋ–Ψ–Φ–Α–Μ–Η–Η –Ω―Ä–Η ―¹–Κ–Α–Ϋ–Η―Ä–Α–Ϋ–Β
YKoshev
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Johnny B Goode
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Gunteer
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews