

–Я–Њ–≤—В–∞—А—П—Й–Є—В–µ —Б–µ –µ–ї–µ–Љ–µ–љ—В–Є, –њ–∞—Б–≤–∞—Й–Є –µ–і–Є–љ –Ї—К–Љ –і—А—Г–≥, –Ї–Њ–Є—В–Њ –Ј–∞–њ—К–ї–≤–∞—В –њ–ї—К—В–љ–Њ —А–∞–≤–љ–Є–љ–∞—В–∞ –Є–ї–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ —Б–∞ —Б—К—Б –Ј–∞–Њ—Б—В—А–µ–љ–Є —Д–Њ—А–Љ–Є –Ї–∞—В–Њ —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є –Є–ї–Є –Ї–≤–∞–і—А–∞—В–Є. –Э–Њ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –≤¬†–њ—А–Є—А–Њ–і–љ–Є—П —Б–≤—П—В —В–µ –љ–µ —Б–∞ —В–∞–Ї–Є–≤–∞.
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ –Њ–њ—А–µ–і–µ–ї—П –љ–Њ–≤ –Ї–ї–∞—Б –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є —Д–Њ—А–Љ–Є, –љ–∞—А–µ—З–µ–љ–Є –Љ–µ–Ї–Є –Ї–ї–µ—В–Ї–Є,¬†–Ї–Њ–Є—В–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В –Ј–∞ –Њ–њ–Є—Б–∞–љ–Є–µ –љ–∞ –љ–∞—З–Є–љ–∞, –њ–Њ –Ї–Њ–є—В–Њ —Б–µ —Д–Њ—А–Љ–Є—А–∞—В –Є –љ–∞—А–∞—Б—В–≤–∞—В –Ј–∞–±–µ–ї–µ–ґ–Є—В–µ–ї–љ–Њ —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–Є–µ –Њ—В –њ–∞—В–µ—А–љ–Є (–Љ–Њ–і–µ–ї–Є) –≤ –ґ–Є–≤–Є—В–µ –Њ—А–≥–∞–љ–Є–Ј–Љ–Є - –Ї–∞—В–Њ –Љ—Г—Б–Ї—Г–ї–љ–Є –Ї–ї–µ—В–Ї–Є –Є —З–µ—А—Г–њ–Ї–Є –љ–∞ –љ–∞—Г—В–Є–ї—Г—Б–Є.
–Я—А–Њ—Б—В–Є —Д–Њ—А–Љ–Є, –Ї–Њ–Є—В–Њ —Б–µ –љ–∞–њ–∞—Б–≤–∞—В –µ–і–љ–∞ –Ї—К–Љ –і—А—Г–≥–∞ –±–µ–Ј –њ—А–Њ–ї—Г–Ї–Є, –Ї–∞—В–Њ –Ї–≤–∞–і—А–∞—В–Є –Є —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є, —Б–∞ –Њ—В–і–∞–≤–љ–∞ –Є–Ј–≤–µ—Б—В–љ–Є –Є —Б–µ –њ—А–µ–і–њ–Њ—З–Є—В–∞—В, –Ј–∞—Й–Њ—В–Њ —Б —В—П—Е —Б–µ —А–∞–±–Њ—В–Є –њ–Њ-–ї–µ—Б–љ–Њ.
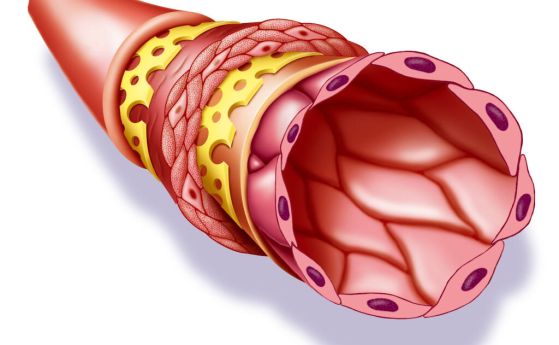
–Т –њ—А–Є—А–Њ–і–∞—В–∞ –Њ–±–∞—З–µ —А—П–і–Ї–Њ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В –Є–і–µ–∞–ї–љ–Њ –њ—А–∞–≤–Є –ї–Є–љ–Є–Є –Є –Њ—Б—В—А–Є –≤—К—А—Е–Њ–≤–µ. –Э—П–Ї–Њ–Є –њ—А–Є—А–Њ–і–љ–Є –Њ–±–µ–Ї—В–Є —Б–µ –і–Њ–±–ї–Є–ґ–∞–≤–∞—В –і–Њ—Б—В–∞—В—К—З–љ–Њ¬†–і–Њ –µ–ї–µ–Љ–µ–љ—В–Є —Б –њ—А–∞–≤–Є —Б—В–µ–љ–Є –Ї–∞—В–Њ –Љ–љ–Њ–≥–Њ—Б—В–µ–љ–Є –Ї–∞—В–Њ –љ–∞–њ—А–Є–Љ–µ—А —Б—К–≤–Ї—Г–њ–љ–Њ—Б—В –Њ—В –Љ–µ—Е—Г—А—З–µ—В–∞ –≤ –њ—П–љ–∞ –Є–ї–Є –љ–∞–њ—Г–Ї–∞–љ–∞—В–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В –љ–∞ –Ь–∞—А—Б. –Э–Њ –Є–Љ–∞ –љ—П–Ї–Њ–Є –Є–Ј–≤–Є—В–Є —Д–Њ—А–Љ–Є, –Ї–∞—В–Њ –љ–∞–њ—А–Є–Љ–µ—А —В—А–Є–Є–Ј–Љ–µ—А–љ–Є—В–µ –Љ–љ–Њ–≥–Њ—К–≥—К–ї–љ–Є—Ж–Є, –Њ—В–Ї—А–Є—В–Є –≤ –µ–њ–Є—В–µ–ї–љ–Є—В–µ –Ї–ї–µ—В–Ї–Є, –њ–Њ–Ї—А–Є–≤–∞—Й–Є –Њ–±–≤–Є–≤–Ї–∞—В–∞ –љ–∞ –Ї—А—К–≤–Њ–љ–Њ—Б–љ–Є—В–µ —Б—К–і–Њ–≤–µ –Є –Њ—А–≥–∞–љ–Є—В–µ, –Ї–Њ–Є—В–Њ —Б–µ –Њ–њ–Є—Б–≤–∞—В –њ–Њ-—В—А—Г–і–љ–Њ.
–°–µ–≥–∞ –У–∞–±–Њ—А –Ф–Њ–Љ–Њ–Ї–Њ—Б (G√°bor Domokos) –Њ—В –Ґ–µ—Е–љ–Њ–ї–Њ–≥–Є—З–љ–Є—П —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В –≤ –С—Г–і–∞–њ–µ—Й–∞, –£–љ–≥–∞—А–Є—П, –Є –Ї–Њ–ї–µ–≥–Є—В–µ –Љ—Г —Б–∞ –Њ—В–Ї—А–Є–ї–Є –Ї–ї–∞—Б —Д–Њ—А–Љ–Є, –Ї–Њ–Є—В–Њ –Њ–њ–Є—Б–≤–∞—В –µ–ї–µ–Љ–µ–љ—В–Є —Б –Є–Ј–≤–Є—В–Є –Ї—А–∞–Є—Й–∞, –Ї–Њ–Є—В–Њ —В–µ –љ–∞—А–Є—З–∞—В –Љ–µ–Ї–Є –Ї–ї–µ—В–Ї–Є. –Ъ–ї—О—З—К—В –Ї—К–Љ —В–µ–Ј–Є —Д–Њ—А–Љ–Є –µ, —З–µ —В–µ —Б—К–і—К—А–ґ–∞—В –≤—К–Ј–Љ–Њ–ґ–љ–Њ –љ–∞–є-–Љ–∞–ї–Ї–Њ –Њ—Б—В—А–Є —К–≥–ї–Є, –Ї–∞—В–Њ –≤ —Б—К—Й–Њ—В–Њ –≤—А–µ–Љ–µ —Б–µ –љ–∞–њ–∞—Б–≤–∞—В –≤—К–Ј–Љ–Њ–ґ–љ–Њ –љ–∞–є-–њ–ї—К—В–љ–Њ.
"–Ґ–µ–Ј–Є —Д–Њ—А–Љ–Є —Б–µ –њ–Њ—П–≤—П–≤–∞—В –≤ –Є–Ј–Ї—Г—Б—В–≤–Њ—В–Њ, –љ–Њ —Б—К—Й–Њ –Є –≤ –±–Є–Њ–ї–Њ–≥–Є—П—В–∞", –Њ–±—П—Б–љ—П–≤–∞ –Ф–Њ–Љ–Њ–Ї–Њ—Б. "–Р–Ї–Њ —А–∞–Ј–≥–ї–µ–і–∞—В–µ —Г—З–∞—Б—В—К—Ж–Є –Њ—В –Љ—Г—Б–Ї—Г–ї–љ–∞ —В—К–Ї–∞–љ, —Й–µ –≤–Є–і–Є—В–µ, —З–µ –Ї–ї–µ—В–Ї–Є—В–µ –Є–Љ–∞—В —Б–∞–Љ–Њ –і–≤–∞ –Њ—Б—В—А–Є –≤—К—А—Е–∞, –Ї–Њ–µ—В–Њ –µ —Б –µ–і–Є–љ –њ–Њ-–Љ–∞–ї–Ї–Њ –Њ—В —В—А–Є—К–≥—К–ї–љ–Є–Ї–∞ - —В–Њ–≤–∞ –µ –Љ–љ–Њ–≥–Њ —Б–њ–µ—Ж–Є–∞–ї–µ–љ –≤–Є–і –Љ–Њ–Ј–∞–є–Ї–∞."
 –Ь–µ–Ї–Є –Њ–±–ї–Є—Ж–Њ–≤–Ї–Є –≤ —А–∞–≤–љ–Є–љ–∞—В–∞: –њ—А–Є–Љ–µ—А–Є –Њ—В –њ—А–Є—А–Њ–і–∞—В–∞ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А–∞—В–∞. –Ъ–Њ–ї–Њ–љ–∞ (1): –њ—А–Є–Љ–µ—А–Є –Ј–∞ –Љ–Њ–љ–Њ–µ–і—А–Є—З–љ–Є (–Љ–Њ–Ј–∞–є–Ї–Є —Б –µ–і–Є–љ-–µ–і–Є–љ—Б—В–≤–µ–љ –µ–ї–µ–Љ–µ–љ—В), –Љ–µ–Ї–Є –Ї–ї–µ—В–Ї–Є. –Ъ–Њ–ї–Њ–љ–Є (2) –Є (3): –њ—А–Є–Љ–µ—А–Є –≤ –њ—А–Є—А–Њ–і–∞—В–∞, –Ї—К–і–µ—В–Њ —Б–µ –њ–Њ—П–≤—П–≤–∞—В —В–µ–Ј–Є –Љ–Њ–і–µ–ї–Є. (a2) –Х—Б—В—Г–∞—А –љ–∞ —А–µ–Ї–∞ –≤ —Б–µ–≤–µ—А–Њ–Ј–∞–њ–∞–і–µ–љ –Ь–∞–і–∞–≥–∞—Б–Ї–∞—А. (b2) –Ш–≤–Є—Ж–Є –љ–∞ –Ј–µ–±—А–∞. (c2) –Э–∞–њ—А–µ—З–љ–Њ —Б–µ—З–µ–љ–Є–µ –љ–∞ —З–µ—А—Г–њ–Ї–∞. (d2) –У–µ–Њ–Љ–µ—В—А–Є—З–µ–љ –Љ–Њ–і–µ–ї –љ–∞ —А–∞—Б—В–µ–ґ –љ–∞ –≤—К—А—Е–∞ –њ—А–Є –≤–Њ–і–Њ—А–∞—Б–ї–Є. (a3) вАЛвАЛ–У–ї–∞–і–Ї–∞ –Љ—Г—Б–Ї—Г–ї–љ–∞ —В—К–Ї–∞–љ. (b3) –Э–∞–њ—А–µ—З–љ–Њ —Б–µ—З–µ–љ–Є–µ –љ–∞ –ї—Г–Ї. (c3) –Я—И–µ–љ–Є—З–µ–љ –Ї–ї–∞—Б (d3) –Ь–µ—А–Є–і–Є–∞–љ–љ–∞ —Б–µ–Ї—Ж–Є—П –љ–∞ –Ї—А—К–≤–љ–Є –Ї–ї–µ—В–Ї–Є. –Ъ–Њ–ї–Њ–љ–∞ (4): –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –љ–∞ –∞—А—Е–Є—В–µ–Ї—В–∞ –Ч–∞—Е–∞ –•–∞–і–Є–і. (a4) Galaxy Soho, –Я–µ–Ї–Є–љ. (b4) –§—Г—В–±–Њ–ї–µ–љ —Б—В–∞–і–Є–Њ–љ, –Ъ–∞—В–∞—А. (c4) Heydar Aliev Center, –С–∞–Ї—Г (d4) –Я—А–Њ–µ–Ї—В –≤ Surfside, –§–ї–Њ—А–Є–і–∞ (2023). –Ъ—А–µ–і–Є—В:¬†Domokos et al.¬†DOI: 10.48550/arXiv.2402.04190; https://arxiv.org/pdf/2402.04190.pdf¬†¬†
–Ь–µ–Ї–Є –Њ–±–ї–Є—Ж–Њ–≤–Ї–Є –≤ —А–∞–≤–љ–Є–љ–∞—В–∞: –њ—А–Є–Љ–µ—А–Є –Њ—В –њ—А–Є—А–Њ–і–∞—В–∞ –Є –∞—А—Е–Є—В–µ–Ї—В—Г—А–∞—В–∞. –Ъ–Њ–ї–Њ–љ–∞ (1): –њ—А–Є–Љ–µ—А–Є –Ј–∞ –Љ–Њ–љ–Њ–µ–і—А–Є—З–љ–Є (–Љ–Њ–Ј–∞–є–Ї–Є —Б –µ–і–Є–љ-–µ–і–Є–љ—Б—В–≤–µ–љ –µ–ї–µ–Љ–µ–љ—В), –Љ–µ–Ї–Є –Ї–ї–µ—В–Ї–Є. –Ъ–Њ–ї–Њ–љ–Є (2) –Є (3): –њ—А–Є–Љ–µ—А–Є –≤ –њ—А–Є—А–Њ–і–∞—В–∞, –Ї—К–і–µ—В–Њ —Б–µ –њ–Њ—П–≤—П–≤–∞—В —В–µ–Ј–Є –Љ–Њ–і–µ–ї–Є. (a2) –Х—Б—В—Г–∞—А –љ–∞ —А–µ–Ї–∞ –≤ —Б–µ–≤–µ—А–Њ–Ј–∞–њ–∞–і–µ–љ –Ь–∞–і–∞–≥–∞—Б–Ї–∞—А. (b2) –Ш–≤–Є—Ж–Є –љ–∞ –Ј–µ–±—А–∞. (c2) –Э–∞–њ—А–µ—З–љ–Њ —Б–µ—З–µ–љ–Є–µ –љ–∞ —З–µ—А—Г–њ–Ї–∞. (d2) –У–µ–Њ–Љ–µ—В—А–Є—З–µ–љ –Љ–Њ–і–µ–ї –љ–∞ —А–∞—Б—В–µ–ґ –љ–∞ –≤—К—А—Е–∞ –њ—А–Є –≤–Њ–і–Њ—А–∞—Б–ї–Є. (a3) вАЛвАЛ–У–ї–∞–і–Ї–∞ –Љ—Г—Б–Ї—Г–ї–љ–∞ —В—К–Ї–∞–љ. (b3) –Э–∞–њ—А–µ—З–љ–Њ —Б–µ—З–µ–љ–Є–µ –љ–∞ –ї—Г–Ї. (c3) –Я—И–µ–љ–Є—З–µ–љ –Ї–ї–∞—Б (d3) –Ь–µ—А–Є–і–Є–∞–љ–љ–∞ —Б–µ–Ї—Ж–Є—П –љ–∞ –Ї—А—К–≤–љ–Є –Ї–ї–µ—В–Ї–Є. –Ъ–Њ–ї–Њ–љ–∞ (4): –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –љ–∞ –∞—А—Е–Є—В–µ–Ї—В–∞ –Ч–∞—Е–∞ –•–∞–і–Є–і. (a4) Galaxy Soho, –Я–µ–Ї–Є–љ. (b4) –§—Г—В–±–Њ–ї–µ–љ —Б—В–∞–і–Є–Њ–љ, –Ъ–∞—В–∞—А. (c4) Heydar Aliev Center, –С–∞–Ї—Г (d4) –Я—А–Њ–µ–Ї—В –≤ Surfside, –§–ї–Њ—А–Є–і–∞ (2023). –Ъ—А–µ–і–Є—В:¬†Domokos et al.¬†DOI: 10.48550/arXiv.2402.04190; https://arxiv.org/pdf/2402.04190.pdf¬†¬†
–Т –і–≤–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Љ–µ–Ї–Є—В–µ –Ї–ї–µ—В–Ї–Є –Є–Љ–∞—В —Б–∞–Љ–Њ –і–≤–∞ –Њ—Б—В—А–Є –≤—К—А—Е–∞, —Б–≤—К—А–Ј–∞–љ–Є —Б –Є–Ј–≤–Є—В–Є –Ї—А–∞–Є—Й–∞, –Є –Љ–Њ–≥–∞—В –і–∞ –њ—А–Є–µ–Љ–∞—В –±–µ–Ј–Ї—А–∞–µ–љ –±—А–Њ–є —А–∞–Ј–ї–Є—З–љ–Є —Д–Њ—А–Љ–Є. –Э–Њ –≤ —В—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П —В–µ–Ј–Є —Д–Њ—А–Љ–Є –Є–Ј–Њ–±—Й–Њ –љ—П–Љ–∞—В –Њ—Б—В—А–Є –≤—К—А—Е–Њ–≤–µ¬†–Є–ї–Є —К–≥–ї–Є. –Э–µ –µ —П—Б–љ–Њ –Ї–Њ–ї–Ї–Њ –Њ—В —В–µ–Ј–Є —В—А–Є–Є–Ј–Љ–µ—А–љ–Є –Љ–µ–Ї–Є –Ї–ї–µ—В–Ї–Є, –Ї–Њ–Є—В–Њ –Ф–Њ–Љ–Њ–Ї–Њ—Б –Є –µ–Ї–Є–њ—К—В –Љ—Г –љ–∞—А–Є—З–∞—В z-–Ї–ї–µ—В–Ї–Є, –Љ–Њ–≥–∞—В –і–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞—В –Є–ї–Є –Ї–∞–Ї –ї–µ—Б–љ–Њ –і–∞ –±—К–і–∞—В —Б—К–Ј–і–∞–і–µ–љ–Є, —А–∞–Ј–Ї–∞–Ј–≤–∞ –∞–≤—В–Њ—А—К—В.
–°–ї–µ–і –Ї–∞—В–Њ –Њ–њ—А–µ–і–µ–ї—П—В –Љ–µ–Ї–Є—В–µ –Ї–ї–µ—В–Ї–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є, –Ф–Њ–Љ–Њ–Ї–Њ—Б –Є –µ–Ї–Є–њ—К—В –Љ—Г —В—К—А—Б—П—В –њ—А–Є–Љ–µ—А–Є –≤ –њ—А–Є—А–Њ–і–∞—В–∞ –Є –Њ—В–Ї—А–Є–≤–∞—В, —З–µ —В–µ —Б–∞ —И–Є—А–Њ–Ї–Њ —А–∞–Ј–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є.
"–Ю—В–Ї—А–Є—Е–Љ–µ, —З–µ –∞—А—Е–Є—В–µ–Ї—В–Є—В–µ —Б–∞ –љ–∞–Љ–Є—А–∞–ї–Є —В–Њ–Ј–Є –≤–Є–і —Д–Њ—А–Љ–Є –Є–љ—В—Г–Є—В–Є–≤–љ–Њ, –Ї–Њ–≥–∞—В–Њ —Б–∞ –Є—Б–Ї–∞–ї–Є –і–∞ –Є–Ј–±–µ–≥–љ–∞—В —К–≥–ї–Є—В–µ", –Њ–±—П—Б–љ—П–≤–∞ –Ф–Њ–Љ–Њ–Ї–Њ—Б.
–Ґ–µ —Б—К—Й–Њ —В–∞–Ї–∞ —Г—Б—В–∞–љ–Њ–≤—П–≤–∞—В, —З–µ z-–Ї–ї–µ—В–Ї–Є—В–µ —Б–∞ —З–µ—Б—В–Њ —Б—А–µ—Й–∞–љ–Є –≤ –±–Є–Њ–ї–Њ–≥–Є—З–љ–Є—В–µ –њ—А–Њ—Ж–µ—Б–Є, –Ї—К–і–µ—В–Њ –Є–Љ–∞ –Є–Ј—А–∞—Б—В–≤–∞–љ–µ –Њ—В –≤—К—А—Е–∞ –љ–∞ –і–∞–і–µ–љ –Њ–±–µ–Ї—В.
–Х–і–Є–љ –Њ—В –љ–∞–є-—П—А–Ї–Є—В–µ –њ—А–Є–Љ–µ—А–Є –Ј–∞ z-–Ї–ї–µ—В–Ї–Є –µ –≤ –Љ–Њ—А—Б–Ї–Є—В–µ —З–µ—А—Г–њ–Ї–Є, –Є–Ј–≥—А–∞–і–µ–љ–Є –Њ—В –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Ї–∞–Љ–µ—А–Є, –Ї–∞—В–Њ –љ–∞–њ—А–Є–Љ–µ—А —З–µ—А—Г–њ–Ї–∞—В–∞ –љ–∞ –љ–∞—Г—В–Є–ї—Г—Б–∞, –Ї–Њ—П—В–Њ –Њ—З–∞—А–Њ–≤–∞ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ, —В—К–є –Ї–∞—В–Њ —Б—В—А—Г–Ї—В—Г—А–∞—В–∞ —Э —Б–ї–µ–і–≤–∞ –ї–Њ–≥–∞—А–Є—В–Љ–Є—З–µ–љ –Љ–Њ–і–µ–ї.
–Ф–Њ–Љ–Њ–Ї–Њ—Б –Є –µ–Ї–Є–њ—К—В –Љ—Г –Ј–∞–±–µ–ї—П–Ј–∞–ї–Є, —З–µ –і–≤—Г–Є–Ј–Љ–µ—А–љ–Є—В–µ —Б—А–µ–Ј–Њ–≤–µ –љ–∞ –≤—Б—П–Ї–∞ –Њ—В –Ї–∞–Љ–µ—А–Є—В–µ –љ–∞ —З–µ—А—Г–њ–Ї–∞—В–∞ –њ—А–Є–ї–Є—З–∞—В –љ–∞ –Љ–µ–Ї–∞ –Ї–ї–µ—В–Ї–∞, –Ј–∞—В–Њ–≤–∞ –Є–Ј—Б–ї–µ–і–≤–∞—В —З–µ—А—Г–њ–Ї–Є—В–µ –љ–∞ –љ–∞—Г—В–Є–ї—Г—Б–∞ —Б –Ї–Њ–Љ–њ—О—В—К—А–µ–љ —В–Њ–Љ–Њ–≥—А–∞—Д, –Ј–∞ –і–∞ –Є–Ј–Љ–µ—А—П—В –Ї–∞–Љ–µ—А–Є—В–µ –≤ —В—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П.
"–Э–µ –≤–Є–і—П—Е–Љ–µ –љ–Є–Ї–∞–Ї–≤–Є —К–≥–ї–Є", –і–Њ–±–∞–≤—П –Ф–Њ–Љ–Њ–Ї–Њ—Б, –Ї–Њ–µ—В–Њ –љ–∞–≤–µ–ґ–і–∞ –љ–∞ –Љ–Є—Б—К–ї—В–∞, —З–µ –Ї–∞–Љ–µ—А–Є—В–µ —Б–∞ –Ї–∞—В–Њ Z-–Њ–±—А–∞–Ј–љ–Є—В–µ –Ї–ї–µ—В–Ї–Є, –Ї–Њ–Є—В–Њ —Б–∞ –Њ–њ–Є—Б–∞–ї–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є.
 –У–µ–Њ–Љ–µ—В—А–Є—П—В–∞ –љ–∞ –Ї–∞–Љ–µ—А–Є—В–µ –љ–∞ –љ–∞—Г—В–Є–ї—Г—Б–∞. –Ъ—А–µ–і–Є—В:¬†Domokos et al.¬†DOI: 10.48550/arXiv.2402.04190; https://arxiv.org/pdf/2402.04190.pdf¬†¬†
–У–µ–Њ–Љ–µ—В—А–Є—П—В–∞ –љ–∞ –Ї–∞–Љ–µ—А–Є—В–µ –љ–∞ –љ–∞—Г—В–Є–ї—Г—Б–∞. –Ъ—А–µ–і–Є—В:¬†Domokos et al.¬†DOI: 10.48550/arXiv.2402.04190; https://arxiv.org/pdf/2402.04190.pdf¬†¬†
"–Ґ–µ —Б–∞ –Є–Ј–Љ–Є—Б–ї–Є–ї–Є –µ–Ј–Є–Ї –Ј–∞ –Њ–њ–Є—Б–≤–∞–љ–µ –љ–∞ –Ї–ї–µ—В—К—З–љ–Є –Љ–∞—В–µ—А–Є–∞–ї–Є, –Ї–Њ–є—В–Њ –Љ–Њ–ґ–µ –і–∞ –µ –њ–Њ-—А–µ–∞–ї–Є—Б—В–Є—З–µ–љ –Њ—В –≥–ї–µ–і–љ–∞ —В–Њ—З–Ї–∞ –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞ –Њ—В —Б—В—А–Њ–≥–Є—П –Љ–Њ–і–µ–ї —Б –Љ–љ–Њ–≥–Њ—Б—В–µ–љ–Є, —Б –Ї–Њ–є—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ —Б–Є –Є–≥—А–∞—П—В –Њ—В —Е–Є–ї—П–і–Њ–ї–µ—В–Є—П", –њ–Њ—Б–Њ—З–≤–∞ –•–∞–Є–Љ –У—Г–і–Љ–∞–љ-–°—В—А–Њ—Б (Chaim Goodman-Strauss) –Њ—В –£–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ –≤ –Р—А–Ї–∞–љ–Ј–∞—Б.
–Ґ–µ–Ј–Є –Љ–Њ–і–µ–ї–Є –±–Є—Е–∞ –Љ–Њ–≥–ї–Є –і–∞ –њ–Њ–і–Њ–±—А—П—В —А–∞–Ј–±–Є—А–∞–љ–µ—В–Њ –љ–Є –Ј–∞ —В–Њ–≤–∞ –Ї–∞–Ї –≥–µ–Њ–Љ–µ—В—А–Є—П—В–∞ –љ–∞ –±–Є–Њ–ї–Њ–≥–Є—З–љ–Є—В–µ —Б–Є—Б—В–µ–Љ–Є, –љ–∞–њ—А–Є–Љ–µ—А –≤ –Љ–µ–Ї–Є—В–µ —В—К–Ї–∞–љ–Є, –≤–ї–Є—П–µ –≤—К—А—Е—Г —Б–≤–Њ–є—Б—В–≤–∞—В–∞ –љ–∞ –Љ–∞—В–µ—А–Є–∞–ї–Є—В–µ, –Ї–Њ–Љ–µ–љ—В–Є—А–∞ –У—Г–і–Љ–∞–љ-–°—В—А–Њ—Б.
"–Э–∞—З–Є–љ—К—В, –њ–Њ –Ї–Њ–є—В–Њ –≥–µ–Њ–Љ–µ—В—А–Є—П—В–∞ –≤–ї–Є—П–µ –≤—К—А—Е—Г –Љ–µ—Е–∞–љ–Є—З–љ–Є—В–µ —Б–≤–Њ–є—Б—В–≤–∞ –љ–∞ —В—К–Ї–∞–љ–Є—В–µ, –µ –љ–∞–Є—Б—В–Є–љ–∞ –Љ–љ–Њ–≥–Њ —Б–ї–∞–±–Њ –њ—А–Њ—Г—З–µ–љ."
–°–њ—А–∞–≤–Ї–∞:¬†SOFT CELLS AND THE GEOMETRY OF SEASHELLS;¬†G. DOMOKOS, A. GORIELY, A. G. HORVATH AND K. REGOS;¬†arXiv DOI: 10.48550/arXiv.2402.04190; https://arxiv.org/pdf/2402.04190.pdf¬†
–Ш–Ј—В–Њ—З–љ–Є–Ї:¬†Mathematicians discover 'soft cell' shapes behind the natural world,¬†New Scientist
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞
–§–Є–Ј–Є–Ї–∞
–Я—А–µ–і—Б–Ї–∞–Ј–∞–љ –µ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –њ–ї–Њ—З–Ї–∞—В–∞ "—И–∞–њ–Ї–∞—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ"

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Я–ї–Њ—З–Ї–∞ "–≤–∞–Љ–њ–Є—А—Б–Ї–Є –∞–є–љ—Й–∞–є–љ" –љ–∞–і–Љ–Є–љ–∞–≤–∞ –њ–Њ—Б–ї–µ–і–љ–Њ—В–Њ –њ–Њ—Б—В–Є–ґ–µ–љ–Є–µ –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ
–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Я—А–Њ–±–Є–≤ –≤ –≥–µ–Њ–Љ–µ—В—А–Є—П—В–∞: –Э–µ–њ–µ—А–Є–Њ–і–Є—З–љ–∞ –Љ–Њ–Ј–∞–є–Ї–∞ —Б –µ–і–љ–∞–Ї–≤–Є –њ–ї–Њ—З–Ї–Є (–≤–Є–і–µ–Њ)




















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews