Следващия път, когато пресичате претъпкан площад, пешеходна пътека или зала на летището, обърнете внимание на пешеходния поток. Вървят ли хората в подредени коридори, в една колона, към съответните си дестинации? Или това е случайна плетеница от лични траектории, докато хората избягват сблъсъци и се промъкват през тълпата?
В статия, публикувана тази седмица в Proceedings of the National Academy of Sciences, изследователи разглеждат общ сценарий, при който пешеходците се движат по натоварена пешеходна пътека. Екипът анализира сценария чрез математически анализ и симулации, като взема предвид многото ъгли, под които хората могат да пресичат, и маневрите за избягване, които могат да направят, докато се опитват да достигнат дестинациите си, същевременно опитвайки се да избегнат сблъсък с други пешеходци по пътя си.
Изследователите също така провеждат експерименти с контролирана тълпа и проучват как реални участници минават през тълпата, за да достигнат определени места. След математическа и експериментална работа екипът идентифицира ключова мярка, която определя дали пешеходният трафик е подреден, така че да се образуват в потока ясни коридори, или неподреден, в който няма забележими пътеки през тълпата. Наречен "ъглово разпространение", този параметър описва броя на хората, които вървят в различни посоки.
Ако тълпата има сравнително малко ъглово разпространение, това означава, че повечето пешеходци вървят в противоположни посоки и се срещат челно с насрещния трафик, например на пешеходна пътека. В този случай е вероятно по-подреден трафик, подобен на коридор. Ако обаче тълпата има по-голямо ъглово разпространение, като например в зала, това означава, че има много повече посоки, които пешеходците могат да поемат, за да пресекат, с по-голям шанс за безредие.
Всъщност изследователите изчисляват точката, в която движеща се тълпа може да премине от ред към безредие. Те откриват, че тази точка е ъглово разпространение от около 13 градуса, което означава, че ако пешеходците не минават направо, а вместо това среден пешеходец се отклонява под ъгъл, по-голям от 13 градуса, това може да насочи тълпата към объркан поток.
"Всичко това е много разумно", заявява Богдан Бачик (Bogdan Bacik)), който е преподавател по приложна математика в MIT. "Въпросът е дали можем да се справим с него точно и математически и къде е преходът. Сега вече имаме начин да определим количествено кога да очакваме да се образуват коридори - спонтанен, организиран, безопасен поток - срещу неорганизиран, по-малко ефективен, потенциално по-опасен поток."
Сред съавторите на изследването са Гжегож Собота (Grzegorz Sobota) и Богдан Бачик от Академията по физика в Катовице, Полша, и Тим Роджърс (Tim Rogers) от Университета в Бат, Великобритания.
Вдясно, вляво, в центъра
Бачик, който е квалифициран в областта на динамиката на флуидите и гранулираните потоци, започва да изучава потока на пешеходците през 2021 г., когато заедно със своите сътрудници разглежда въздействието на социалното отдалечаване и начините, по които хората могат да се движат помежду си, като същевременно поддържат безопасни разстояния. Тази работа ги вдъхновява да разгледат по-общо динамиката на потока на тълпите.
През 2023 г. той и сътрудниците му изследват "образуването на коридори" - явление, при което частици, зърна и, да, хора са наблюдавани да образуват спонтанно коридори, движейки се в една линия, когато са принудени да пресекат даден район от две противоположни посоки. В тази работа екипът идентифицира механизма, по който се образуват такива коридори, който Бачик обобщава като "дисбаланс на завиване наляво спрямо завиване надясно". По същество те откриват, че веднага щом нещо в тълпата започне да прилича на лента, индивидите около тази зараждаща се лента или се присъединяват, или са принудени да се прехвърлят на една от двете ѝ страни, вървейки успоредно на първоначалната лента, която другите могат да последват. По този начин тълпата може спонтанно да се организира в регулярни, структурирани коридори.
"Сега се питаме колко устойчив е този механизъм?" Бацик отбелязва, че този механизъм е много надежден. "Работи ли само в тази много идеализирана ситуация, или формирането на коридори може да търпи някои несъвършенства, като например някои хора да не вървят идеално праволинейно, както може да се случи в тълпата?"
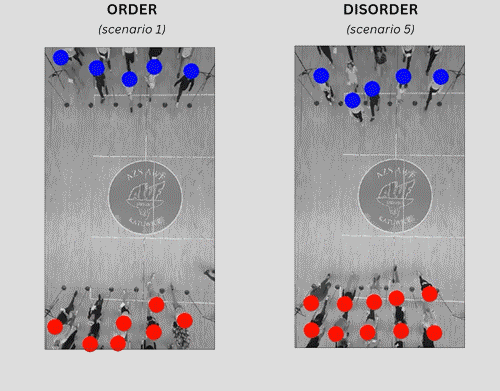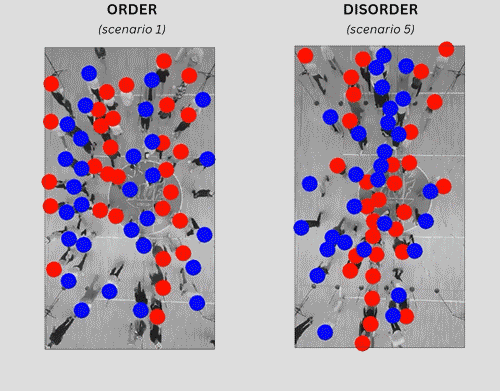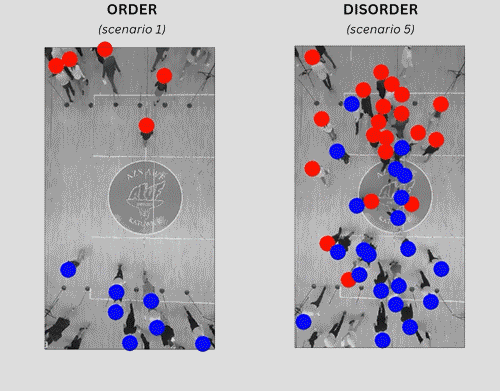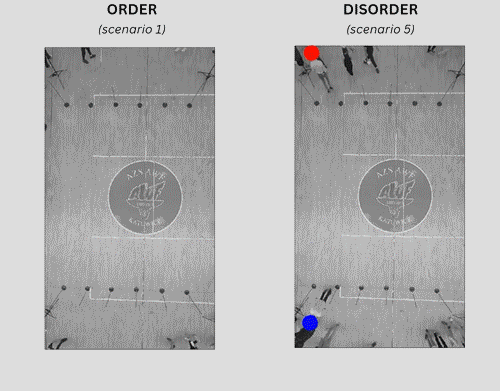Изследователите провеждат контролирани експерименти с тълпа и проучват как реални участници минават през тълпата, за да достигнат определени места. Те идентифицират ключова мярка, „ъглово разпространение“, която определя дали пешеходният трафик е подреден или неподреден. Кредит: K.A. Bacik,G. Sobota,B.S. Bacik,& T. Rogers, Order–disorder transition in multidirectional crowds, Proc. Natl. Acad. Sci. U.S.A. 122 (14) e2420697122, https://doi.org/10.1073/pnas.2420697122 (2025)
Смяна на лентата
За новото си изследване екипът се стреми да идентифицира ключов преход в потока на тълпите: Кога пешеходците преминават от подредено, подобно на лента движение, към по-малко организирано, разхвърляно движение? Изследователите първо изследват въпроса математически, с уравнение, което обикновено се използва за описание на флуиден поток от гледна точка на средното движение на много отделни молекули.
"Ако си представим, че цялата тълпа се движи като флуид, а не отделни индивиди, можем да използваме описания, подобни на тези на флуидите", обяснява Бачик. "Това е изкуството на усредняването, при което, дори ако някои хора могат да пресичат по-настойчиво от други, тези ефекти вероятно ще се усреднят в достатъчно голяма тълпа. Ако се интересуваме само от глобалните характеристики, като например има ли коридори или не, тогава можем да правим прогнози, без да имаме подробни познания за всички в тълпата."
Бачик и колегите му използват уравненията на флуидния поток и ги прилагат към сценария с пешеходци, пресичащи пешеходна пътека. Екипът променя някои параметри в уравнението, като например ширината на канала за флуиди (в този случай пешеходната пътека) и ъгъла, под който молекулите (или хората) пресичат, както и различните посоки, в които хората могат да "избягват сблъсъци" или да се движат един около друг, за да избегнат сблъсък.
Въз основа на тези изчисления изследователите установяват, че пешеходците на пешеходна пътека е по-вероятно да образуват коридори, когато вървят сравнително праволинейно, от противоположни посоки. Този ред се запазва до голяма степен, докато хората не започнат да пресичат под по-крайни ъгли. Тогава уравнението прогнозира, че потокът от пешеходци вероятно ще бъде неорганизиран и ще се образуват малко или никакви коридори.
Изследователите решават да проверят дали математиката се потвърждава в действителност. За тази цел те провеждат експерименти в спортна зала, където записват движенията на пешеходците с помощта на горна камера. Всеки доброволец носел хартиена шапка, на която бил изобразен уникален баркод, който камерата можела да проследи.
При експериментите си екипът определил на доброволците различни начални и крайни позиции от противоположните страни на симулирана пешеходна пътека и им поставил задачата да преминат едновременно през пешеходната пътека до целевото място, без да се блъскат в никого. Експериментът е повторен многократно, като всеки път доброволците заемат различни начални и крайни позиции. В крайна сметка изследователите успели да съберат визуални данни за множество потоци от хора, като пешеходците заемали много различни ъгли на пресичане.
Когато анализирали данните и отбелязали кога спонтанно се образуват коридори и кога не, екипът установил, че както предсказва уравнението, ъгловото разпространение има значение. Експериментите им потвърждават, че преходът от подреден към неподреден поток настъпва някъде около теоретично предвидените 13 градуса. Тоест, ако средностатистическият човек се отклони на повече от 13 градуса от правата линия, потокът от пешеходци може да премине в безпорядък, с малко образуване на коридори. Нещо повече, те откриват, че колкото повече безпорядък има в тълпата, толкова по-неефективно е нейното движение.
Екипът планира да провери прогнозите си върху реални тълпи и пешеходни улици.
Справка: K.A. Bacik,G. Sobota,B.S. Bacik,& T. Rogers, Order–disorder transition in multidirectional crowds, Proc. Natl. Acad. Sci. U.S.A. 122 (14) e2420697122, https://doi.org/10.1073/pnas.2420697122 (2025)
Източник: Mathematicians uncover the logic behind how people walk in crowds, Jennifer Chu, MIT News
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
dolivo
Полетът на Starliner до МКС през 2024 г. е бил много по-драматичен, отколкото знаем (видео)
dolivo
Загадка: Как са се озовали инструменти, подобни на неандерталските, в Източна Азия - разстоянието е континент?
dolivo
Варна става част от Световно космическо парти с кратки видеоклипове и техно груув парти
Имане Хелиф
Анусът може да е еволюирал от отвор, първо използван за отделяне на сперма