Земята
Суровините от критично значение не са само ресурс, те са новото политическо и дипломатическо оръжие

Животът
Един вид пеперуди използват отрова, за да привлекат партньори. Как го правят?
Медицина
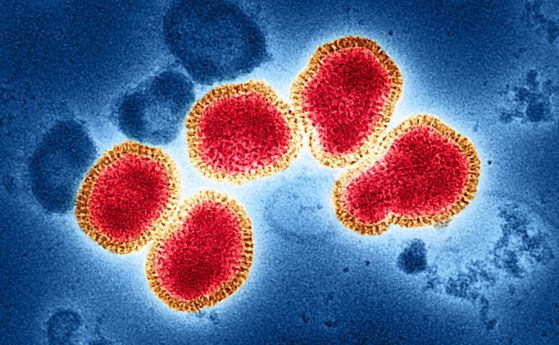
Грипът се смята за най-голямата пандемична заплаха

Космос
Лилавото може да е новото зелено за извънземния живот

Медицина
Науката за разбитите сърца: Защо раздялата боли

Земята
Оранжево "марсианско" небе над Атина заради прашна буря от Сахара
Медицина
"Ехо, мами! Днес ще си говорим за педофили". Кой е той и как да опазим децата си от него? Обяснява Надя Йорданова

Космос
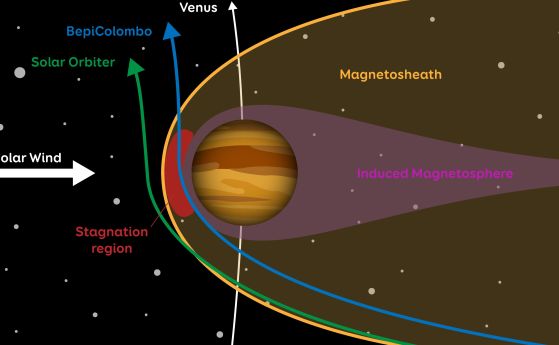
Космически кораб на НАСА и руски сателит едва не се сблъскват

Животът
Тасманийската планинска скарида - жив фосил отпреди 200 милиона години

Скептик
"Дубайският кемтрейлс" - обяснението на специалист

Човекът
Мястото на смъртта на първия император на Рим, вероятно е намерено от японски изследователи в Южна Италия

Космос
За първи път от пет месеца Вояджър 1 възобнови съобщенията до Земята

Човекът
Материята в движение: Ролята на диалектическата философия в науката

Земята
Кои бяха най-опасните метеорологични явления по света през 2023 година?

Човекът
Индоевропейски езици: Ново изследване съгласува двете доминиращи хипотези за произхода им

Физика
Грешката в хипотезата за мултивселената
Физика
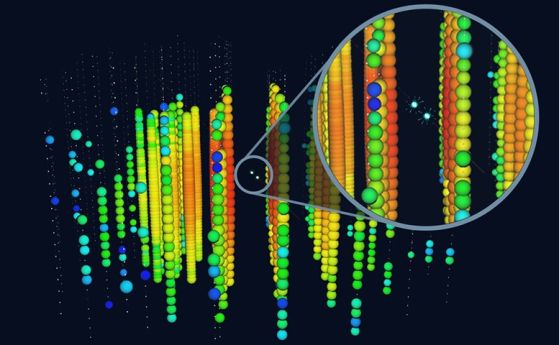
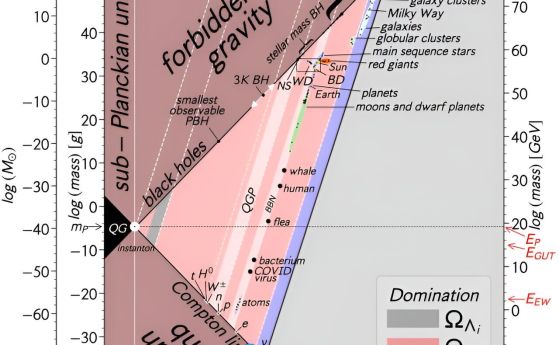
Тази графика показва всички обекти във Вселената

Космос
Астероидната мисия Psyche на НАСА успешно стартира с ракетата Falcon Heavy след 1-годишно забавяне
Космос
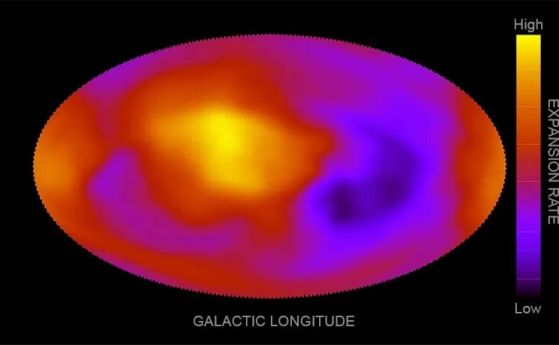
Топ астрономи се събират, за да се изправят срещу възможността, че са грешали за Вселената

Животът
Астероидът, убил динозаврите, не е предизвикал дълга "ядрена зима"

Физика
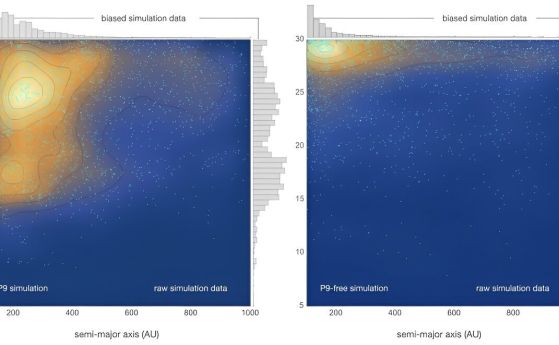
Деветата планета може да докаже, че концепцията за тъмната материя е излишна

Физика
Вселената вече е в своята шеста и последна епоха

Космос
Шест космически мисии, които очакваме с нетърпение през 2024 г

Животът
Един вид пеперуди използват отрова, за да привлекат партньори. Как го правят?

Животът
Тасманийската планинска скарида - жив фосил отпреди 200 милиона години

Животът
Поляризираната лунна светлина помага на мравките да намерят пътя си към дома

Животът
Тази пеперуда е еволюирала от два хибрида. Време ли е за промяна на дефиницията за вид

Човекът
Мястото на смъртта на първия император на Рим, вероятно е намерено от японски изследователи в Южна Италия

Човекът
Следи от праисторическа човешка дейност са открити в лавова тръба

Човекът
Разплитането на енигматичния произход на най-новия вид в човешкото семейство

Човекът
Горещ март 2024 г. – месецът донесе летни температури и счупи нови рекорди

Човекът
Възможно е Стоунхендж да е свързан и с Луната

Медицина
Гените, които ни предпазват от алкохолизъм, повишават вероятността от рак и други болести

Медицина
Грипът се смята за най-голямата пандемична заплаха

Медицина
Науката за разбитите сърца: Защо раздялата боли

Медицина
"Ехо, мами! Днес ще си говорим за педофили". Кой е той и как да опазим децата си от него? Обяснява Надя Йорданова

Скептик
"Дубайският кемтрейлс" - обяснението на специалист

Скептик
Скандалът със свръхпроводимостта: История за измама на една изгряваща звезда

Скептик
"Тайната" обещава, че можем да получим всичко, стига да го искаме. Но ако това е вярно, защо всички не сме богати и известни?

Скептик
Честит Ден на скептика!

Защо
Колко големи могат да станат снежинките?

Защо
Има ли "горе" и "долу" в космоса?

Защо
Възможно ли е Земята да се намира в черна дупка?

Защо
Ягодите са орехи, а пъпешите са ягоди

Защо
Колко най-високо може да се издигне една планина на Земята?
Хумор
Водопровод и математически анализ
Хумор
Влиза инженер-химик в аптеката ...

Хумор
Хайзенберг, Шрьодингер и Ом пътуват заедно
Хумор
Виц на деня: 4 юни