Числовият ред на Фибоначи, който се образува като всеки негов следващ член е сбор от два предходни, е обгърнат с математическа магия. Наречени на италианския математик Леонардо от Пиза (по-известен като Фибоначи), тази поредица от числа (0, 1, 1, 2, 3, 5, 8, 13...) понякога се проявяват по удивителен начин в красиви математически спирали и къде ли не в самата природа.

Въпреки че не обяснява всяка "спирала" или повтаряща се и прогресираща структура, тази поредица наистина обяснява много.

Математическите й корени обаче са едновременно по-прости и по-сложни, отколкото мнозина могат да си представят.

Един от най-очарователните факти за естествения свят е, че толкова много същества в него - както биологични, така и чисто физически - се подчиняват на специфичен набор от модели и съотношения. Много галактики показват спираловидни форми и структури, както и голямо разнообразие от растителни структури: шишарки, ананаси и слънчогледови пити. Амонитите, животни с черупки, които са изчезнали преди повече от 60 милиона години, също показват този спирален модел, където една от ключовите характеристики на спиралите е, че всеки следваща обиколка показва специфично съотношение спрямо размера на предишната.

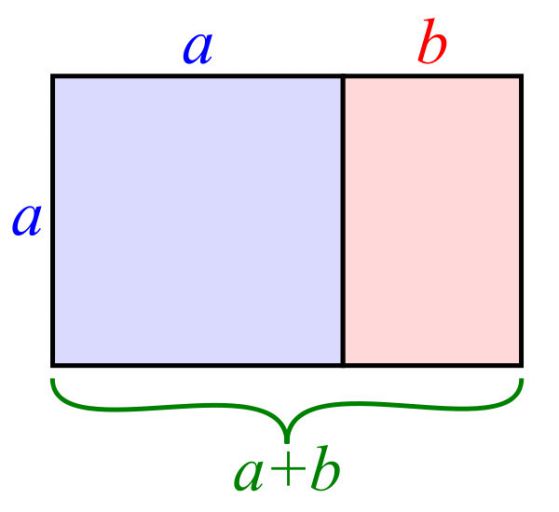Две числа — a и b, принадлежат към златното сечение, ако тяхното съотношение а/b е равно на съотношението на техния сбор върху по-голямото от тях (а+b)/a.

Това съотношение, във всяка такава структура, често е изключително близко до съотношението на две съседни числа в последователността на Фибоначи. Тази математически ред, често преподаван на деца, просто започва с числата "0" и "1" и след това получава следващия член в последователността чрез сбора на двата предходни члена. Това е може би най-известният математически ред от всички, но какво обяснява модела на последователността и дали тя наистина е неразривно свързана с природата? Отговаря Итън Сийгъл.

Наистина, на пръв поглед "спиралните" структури в галактиките може да изглеждат като по Фибоначи, но реално ли е това или просто умовете ни намират връзки там, където ги няма?

Този изглед на MIRI, от JWST и сътрудничеството PHANGS, на спиралната галактика NGC 1566 показва нагорещени, прашни и ядрени характеристики, които са напълно невидими за други обсерватории, наблюдаващи в оптични/UV и дори радиовълни. Тази мрежа от прахови нишки се среща навсякъде в спиралите, но самите спирали не следват модела, който може да се очаква от златното сечение или последователността на Фибоначи.
Кредит:  NASA/ESA/CSA/Judy Schmidt

Галактически и други физически спирали

Когато става въпрос за спирали, които естествено се срещат в чисто физическите науки, "спиралните галактики" несъмнено са най-известните сред тях. Някъде малко над половината от всички известни големи, близки, масивни галактики имат спирални форми и структури в тях, но когато ги изследваме математически, се оказва, че много малко от тях следват модел, подобен на спиралата на Фибоначи.

Важно е, че спиралата на Фибоначи е самоподобна, което означава че ако намалите или увеличите мащаба, ще видите да се повтаря същият структурен модел. Спиралните структури, наблюдавани в галактиките, не правят това по два отделни начина, тъй като:

1. вътрешността на спиралните галактики рядко е спираловидна по целия път до центъра, а по-скоро завършва в асиметрична галактическа издутина или лента,
2. и външната част на тези галактики - в които звездите, газът и прахът са до голяма степен ограничени до диск - по-добре се апроксимират до дъга, крива, част от кръг, отколкото от която и да е "спираловидна" структура.

Не забравяйте, че спиралните ръкави в една галактика са причинени от вълни на плътност и от усукването на галактиката с течение на времето. Има няколко забележителни характеристики, които съществуват в някои спирални галактики, които показват модел, подобен на Фибоначи, върху тези междинни региони, но това не е норма.

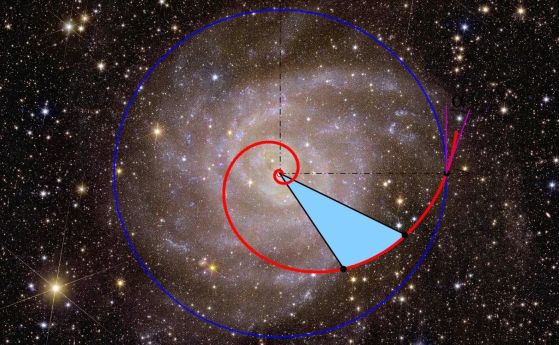
Въпреки че някои спирални галактики може да имат характеристики, които наистина изглеждат като следващи модела на Фибоначи, това не се вижда при повечето спирални галактики, нито в повечето характеристики дори в рамките на галактики, които грубо се подчиняват на този модел. Въпреки че последователността на Фибоначи се появява ясно на много места, спиралните галактики не са сред тях. Кредит: NASA/CBSI

Няколкото спирали, които показват подобен на Фибоначи модел, са част от клас спирали, известни като спирални галактики с подредена структура, и те представляват само около 1 на 10 спирални галактики, за разлика от най-често срещаните типове с многораменни спирали (включително Млечния път) и втория най-често срещан тип с фина спирална структура с много ленти, известни като флокулентни спирални галактики. Тези спирали с "подредена структура" са почти изключително галактики, които наскоро са претърпели или в момента са подложени на гравитационно взаимодействие на близка спътникова галактика и само това външно гравитационно влияние дърпа най-външните ръкави и характеристики във форми, които са по-съвместими с намерените съотношения в последователността на Фибоначи.

Въпреки че има много спирални форми, които възникват от чисто физически, небиологични процеси в природата - от водовъртежи, които се образуват във водни тела до въздушните форми на ураганни облаци - нито една от тези спирали не прилича на спиралата на Фибоначи, когато се стигне до действителните математически детайли на техните структури на устойчива основа. Може да успеем да направим "моментна снимка", където една или повече от характеристиките показват съотношения, които са в съответствие със съотношенията в последователността на Фибоначи за конкретен момент, но тези структури продължават да се променят. Подобните на Фибоначи модели, наблюдавани в спиралните галактики, са само в нашите очи, а не физическа истина за Вселената.

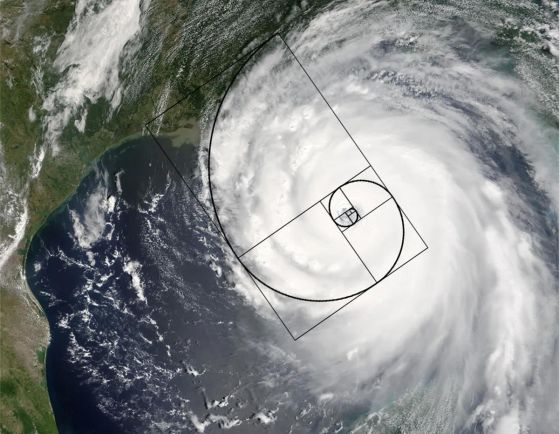Тази сателитна снимка на урагана Катрина изглежда показва спираловидна структура на облаците. Въпреки че може да е изкушаващо да свържем този модел със спиралата на Фибоначи, връзката е фалшива, тъй като нито този, нито повечето урагани имат спирален модел, който се подчинява на златното сечение. Кредит: NASA

Биологични спирали на Фибоначи

Въпреки това моделите и съотношенията на Фибоначи, открити в много биологични организми, включително в растенията, наистина са свързани с реда на Фибоначи, както по математически строг начин, така и поради еволюционна причина, която има рационален смисъл. Нека първо да се заемем с биологичните свойства и да се върнем към математиката.

Нека си представим растение, примитивно растение при това. То има способността да генерира собствена енергия от слънчева светлина, хранителни вещества в почвата, вода и въглероден диоксид и да произвежда захари (съхранена енергия) чрез процеса на фотосинтеза, който протича в листата. Когато покълне от семе, трябва да развие листата си навън и някъде в генетичния код ще има част от информацията, която казва под какъв ъгъл да постави "следващо листо" спрямо предишното листо.

Едно от решението е един опростен път като при растението детелина и просто да постави три листа под ъгъл от 120° едно спрямо друго и да се образува триъгълен модел. Проблемът с този метод е, че е ефективен, но не и мащабируем. Не се срещат гигантски детелинови дървета, защото не може да се мащабират: когато се поставят три листа под ъгъл от 120° едно спрямо друго, няма къде да се постави "следващото" листо, което няма да е много ефективно, или ще бъде под сянката на предишните листа, или ще блокира светлината за предишните листа, събиращи слънчева светлина.

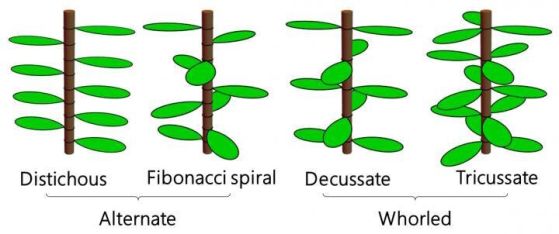Диаграма, обясняваща етапите на растение, използвайки последователността на Фибоначи. Подредбите на листата върху растенията могат да бъдат или с един лист на възел (редуващ се) или с два листа на възел (повтарящ се), като простият двоен модел се среща в бамбука, но по-ефективният спирален модел на Фибоначи, следващ златното сечение, се появява в много растения, включително сукуленти като алое. Кредит: Takaaki Yonekura/University of Tokyo

Но какво ще стане, ако трябва да се кодира най-ефективния начин за извеждане на "следващия лист" въз основа на това къде е поставен предишния лист? Разбира се, за общо три листа, 120° е математически перфектен, но за произволен брой листа, това не върши работа.

Представете си растение, което расте нагоре и току-що е пуснало първото си листо. Докато расте нагоре и тръгне да пуска втория си лист, под какъв ъгъл трябва да излезе, така че не само първият и вторият лист, но и третият, четвъртият, петият, шестият и т.н. да получат максимално количество слънчева светлина?

Отговорът е, че всяко листо следващото листо трябва да бъде поставено точно около 61,8% от пълния кръг от предходното листо. За окръжност с 360° в нея това съответства на ъгъл от 222,5°, а точното число, на което съответства, е това, което математиците определят като - ψ, което е равно на (√5 – 1)/2, или приблизително 0,61803398875. Положителната му версия, (√5 + 1)/2, е известна като φ или златното сечение и е 1/(-ψ), което е равно на 1 + (- ψ), както и съотношението между всяко число на Фибоначи и неговия предшественик.

Ако продължави да поставя листа под този ключов ъгъл, 222,5°, спрямо предишния лист, с шарките на листата ще се образува спирала на Фибоначи. Същото математическо свойство, кодирано в ананаси, шишарки и други, обяснява защо биологичните организми често показват числа, намиращи се в редицата на Фибоначи.

Отговорът е, че за всяко листо следващото листо трябва да бъде поставено точно около 61,8% от пълния кръг от предходното листо. За окръжност с 360° в нея това съответства на ъгъл от 222.5°, а точното число, на което съответства, е това, което математиците определят като –ψ , което е равно на (√5 – 1)/2, или приблизително 0,61803398875. Положителната версия на това, (√5 + 1)/2, е известна като φ или златното съотношение и е 1/(-ψ), което е равно на 1 + (- ψ), както и: съотношението между всяко число на Фибоначи и неговия предшественик. Ако продължавате да поставяте листа под този ключов ъгъл, 222.5°, спрямо предишния лист, моделът на листата ще образува спирала на Фибоначи. Същото математическо свойство, кодирано в ананаси, шишарки и други, обяснява защо биологичните организми често показват числа, намиращи се в редицата на Фибоначи.

Вътрешността на цветето има много компоненти, подредени в шаблон, който е очертан (вложка) в синьо и циан във всяка посока, с 21 сини линии и 13 цианови линии. И двете са последователни числа на Фибоначи. Кредит: Alvesgaspar & RDBury/Wikimedia Commons; Добавки: E. Siegel

Математиката на Фибоначи

Но по-големият въпрос не е "защо последователността на Фибоначи се среща в природата", а по-скоро "какво е това, което определя разпространението на реда на Фибоначи"?

Доста лесно е да се изчислят числата на Фибоначи: всичко, което трябва да се направи, е да се съберат първите две числа: "0" и "1", за да се започне, и след това всеки следващ член от сбора на предишните два члена на реда. Така първите няколко члена на последователността на Фибоначи са:

• 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 и т.н.

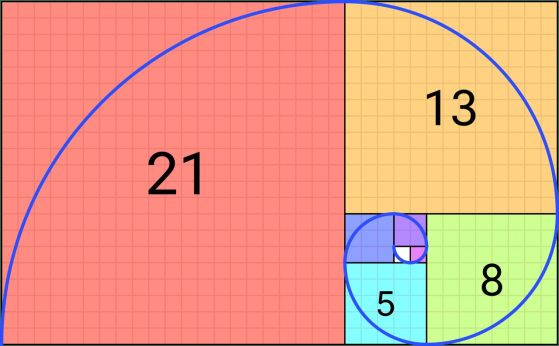Спиралата на Фибоначи, показана тук, се генерира чрез превръщане на всяко число в последователността в квадрат, след което се генерира следващото число чрез поставяне на съседен квадрат с дължина на страната, определена от сбора на предишните два квадрата, в посока обратна на часовниковата стрелка около последните членове. За големи числа тези съотношения се доближават до стойност, известна като златно сечение. Кредит: Romain/Wikimedia Commons

Сега, нека да разгледаме съотношенията на всеки два последователни члена един спрямо друг и да разберем какво е съотношението на "следващия" член към "предходния" член, започвайки с двете "1" в последователността (така че да не стигаме до деление на нула).

• 1 ÷ 1 = 1,0,
• 2 ÷ 1 = 2,0,
• 3 ÷ 2 = 1,5,
• 5 ÷ 3 = 1,66666…,
• 8 ÷ 5 = 1,6,
• 13 ÷ 8 = 1,625,
• 21 ÷ 13 = 1,61538462…,
• 34 ÷ 21 = 1,61904762…,

и така нататък. Както може да видите, членовете варират между малко по-малко от φ, златното сечение, и малко по-голямо от φ, но се приближаваме към него все повече.

Съотношението на всеки член в редицата на Фибоначи към предходния член бързо се доближава до стойност, известна като златно сечение: отгоре и отдолу с всеки следващ член. Приближението става все близко и по-близко много бързо, така че отклонението от истинската стойност е почти незабележимо с просто око само след няколко изчисления. Кредит: A. Kursat ERBAS

Лесно е да видите колко бързо се доближаваме до златното сечение. Ако погледнем последните три числа, написани по-горе - 2584, 4181 и 6765 - се вижда, че съотношенията:

• 4181 ÷ 2584 = 1,61803405573 и
• 6765 ÷ 4181 = 1,61803396317,

много бързо и много близо до самото златно сечение, φ. Ако се повишим само с още няколко числа до 10946, 17711, 28657, 46368 и след това 75025 (последното число на Фибоначи под 100 000), ще открием, че съотношението 75025 ÷ 46368 = 1,61803398896: прогноза за златното сечение, която се различава едва след като се стигне до 11-та значима цифра.

Оказва се, че няма нищо особено и в началната точка на редицата на Фибоначи. Може да започнете с произволни две неотрицателни числа, които харесвате, като поне едно от тях е различно от нула: не е необходимо да са "0" и "1", не е необходимо да са цели числа, не е необходимо да са близо едно до друго.

Всичко, което трябва да направите, е да следвате същата формула, като събирате първите две числа, за да направите следващото (третото) число, и след това да добавите това число с предишното, за да направите следващото следващо число и т.н. Без значение с кои числа започвате, съотношението на всеки две последователни числа бързо ще се доближи до φ, златното сечение.

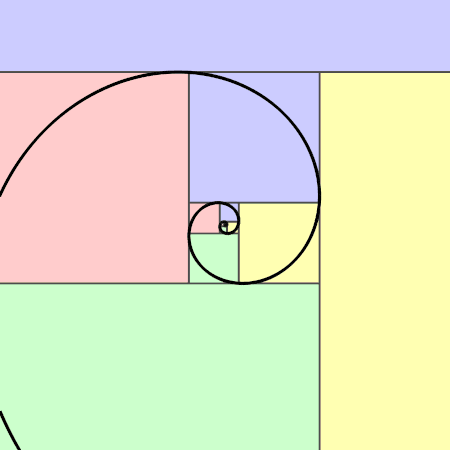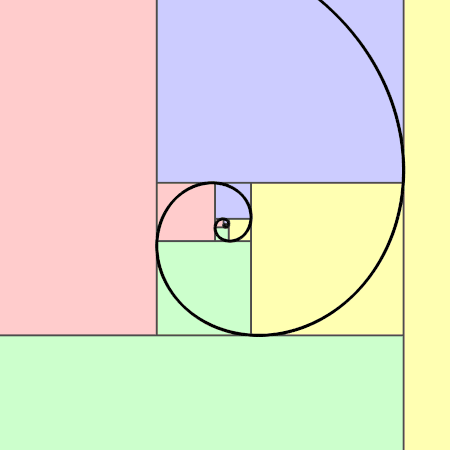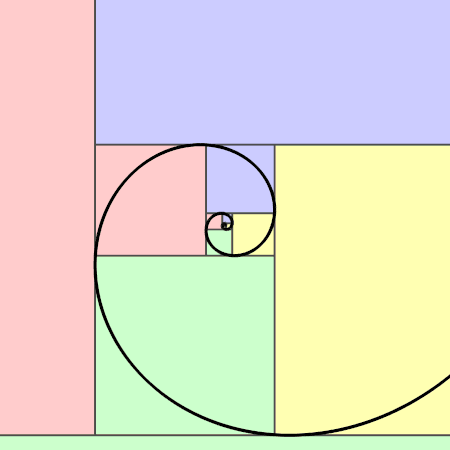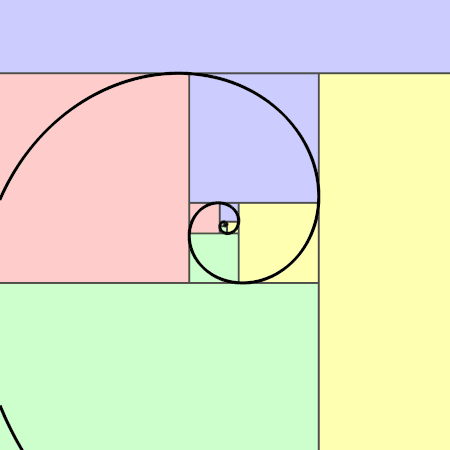Логаритмичната златна спирала, известна още като спирала на Фибоначи, е самоподобен, самоповтарящ се модел, който възниква чрез конструиране на всеки следващ член в последователността чрез сумиране на предходните два члена. Въпреки че това е кодирано само приблизително в природата, математическата връзка, която е в основата му, е точна. Кредит: Jahobr/Wikimedia Commons

Дроб, която генерира реда на Фибоначи

А има ли по-лесен начин да се генерират всички числа на Фибоначи, без да се налага да се събира всеки член от предишните два?

Оказва се, че има и това е невероятен математически куриоз. Ключът, вярвате или не, е 11-то число в редицата на Фибоначи: 89.

Какво му е толкова специалното в числото 89? На повърхността не толкова.

Двете съотношения, от които е част, 89 ÷ 55 и 144 ÷ 89, не изглеждат специални: излизат съответно 1,6181818… и 1,6179775….

Но ако вместо това вземем друго съотношение: 1 към числото 89, се забелязва нещо малко странно. Ако го се напише с повече знаци след десетичната запетая, ще откриете, че се появяват първите няколко числа от редицата на Фибоначи.

• 1/89 = 0,011235955…,

в който можем лесно да видим първите няколко разпознаваеми числа: 0, 1, 1, 2, 3 и 5.

Може да погледнете "9" и да си помислите, че там се обърка, но не забравяйте, че следващият двете числа са 8 и 13 и затова включваме някакъв вид "пренасяне", което може да трансформира това, което се надяваме да бъде "8" в "9", ако направим нашето добавяне правилно. Има един хитър трик, който може да се използва, за да се тества модела на Фибоначи малко по-обширно.

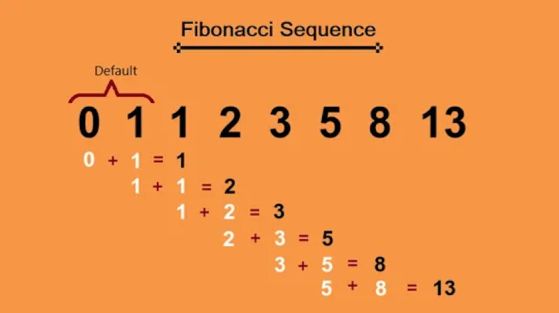Първите осем члена на последователността на Фибоначи, с показаните трети до осми член, генерирани чрез сумиране на всеки от предходните два члена. Тази проста последователност, кръстена на математик от 13-ти век, но известна от преди повече от 1000 години, се появява в природата, но има своите корени в математиката. Кредит: Jean Claude Adjanohoun/Linkedin

Вместо да използваме числото 89, нека помним, че използваме основа 10, така че нека си помогнем, като добавим "9" от двете страни на това число 89, за да създадем вместо това дробта 1/9899. Когато разширим с повече знаци след десетичната запетая този път - ето какво получаваме:

• 1/9899 = 0,0001010203050813213455…,

и изведнъж виждаме да се появяват много повече числа на Фибоначи. Какво ще стане, ако опитаме да добавим още няколко 9 от двете страни? Да кажем, 1/99989999? Сега с повече знаци след десетичната запетая става:

• 1/99989999 = 0,00000001000100020003000500080013002100340055008901440233037706100987159725844181…,

и можем да видим, че се появяват все повече и повече членове, преди да се натъкнем на грешки при "пренасяне". Ако се добавят още девятки от двете страни на знаменателя и ще се получи формула за генериране на числата на Фибоначи, по ред, появяващи се в дробта, доколкото решите да я разширявате.

Може просто да решите колко цифрено число от реда на Фибоначи желаете и да добавите толкова девятки в равни количества, от двете страни на "89" в знаменателя. Тогава знаците след десетичната запетая ще ви покажат гарантирано всички числа на Фибоначи с по-малко цифри, отколко е броят на девятките, които поставяте от двете страни на знаменателя на дробта.

От разширяването на дробта 1/9999899999, където имате четири "9" от двете страни на ключовото число "89" в знаменателя, може да видите първите 24 числа на реда на Фибоначи, всяко с 5 цифри, докато проблема с "пренасянето" започва да смущава последователността. Кредит: Krishnan/Cantor’s Paradise

Но има дълбока причина всичко се свежда до "89".  Представете си, че събираме членовете в редицата на Фибоначи, като разделяме всеки член на 10⁽ⁿ⁺¹⁾ , където n е номерът на този член. С други думи, това означава, че нашата адитивна последователност изглежда така:

• 0,0 + 0,01 + 0,001 + 0,0002 + 0,00003 + 0,000005 + 0,0000008 + 0,00000013 + 0,000000021 + 0,0000000034 + 0,00000000055 + 0,00000000008 9 + 0,0000000000144 + ….,

и така нататък. Сега нека направим малък математически трик: ще умножим тази редица по 10 и след това ще извадим оригиналната редица от нея (давайки ни девет пъти оригиналната редица). Това изглежда така (пренебрегвайки първия член, който е равен на нула):

• 0,1 + 0,01 + 0,002 + 0,0003 + 0,00005 + 0,000008 + 0,0000013 + 0,00000021 + 0,000000034 + 0,0000000055 + 0,00000000089 + 0,00000000014 4 + … – (0,01 + 0,001 + 0,0002 + 0,00003 + 0,000005 + 0,0000008 + 0,00000013 + 0,000000021 + 0,0000000034 + 0,00000000055 + 0,00000000089 + 0,0000000000144 + …),

което, ако вземем първия член отделно и след това групираме всеки следващ член заедно, ни дава:

• 0,1 + (0 + 0,001 + 0,0001 + 0,00002 + 0,000003 + 0,0000005 + 0,00000008 + 0,000000013 + …),

което ни показва, че девет пъти оригиналната последователност се равнява на 0,1 + една десета от оригиналната последователност!

Или, с други думи,  оригиналната редица, т.е. сумата от числата в редицата на Фибоначи, сортирани по десетични знаци, е равна на 0,1/8,9 или 1/89. И затова редицата на Фибоначи не е присъща на природата, а по-скоро на чистата математика. Появява се в природата, защото от златното сечение има биологична полза, но където и да се появява във физическите науки, включително в някои спирални галактики, това е само по чиста случайност.

Източник: Ask Ethan: What explains the Fibonacci sequence?, Ethan Siegel, Big Think

Още по темата

07/08/2023

Математика

Разкрита е изненадваща връзка между чистата математика и генетиката

19/06/2023

Животът

Изследване на вкаменелости оспорва теорията за спиралите на Фибоначи в природата

31/05/2016

Животът

Всички слънчогледи ли "предпочитат" реда на Фибоначи

12/12/2014

Математика

Числовият ред на Фибоначи