
Познато ни е R, ефективното репродуктивно число на заболяването - броят на хората, заразèни средно от един зарàзен човек. R ни помага да разберем какво се случва с разстространението на болестта: R >1 означава, че епидемията ще расте, R = 1 означава, че сме на плато, R < 1 означава, че епидемията ще намалее. Но дава ли достатъчно ясна представа как ще се развие пандемията - с колко ще се увеличат или намалеят случаите след седмица например?
Поредната статия от цикъла "Математика на пандемията" ще даде отговор на този въпрос.
Обърнете внимание, че числото R, за което чуваме в новините всеки ден, се променя в хода на епидемията, това е ефективното репродукционно число, а не основното репродукционно число, R 0 , за което също може да сте чували. Каква е разликата?
R 0 е средният брой хора, които зарàзен човек може да зарази, като се има предвид, че всеки в популацията е податлив. В реалния живот нямаме работа с напълно податлива популация - някои са преболедували, други са ваксинирани или може да са изолирани от останалата част от населението.
Затова в повечето ситуации от реалния живот трябва да разглеждаме ефективното репродуктивно число на болестта, понякога обозначаван с R: средният брой, който заразеното лице продължава да заразява в популация, където някои хора са имунизирани (или са налице някои други интервенции). Разбира се R0 и R са свързани. Пишем s за дела от населението, което е податливо на заразяване, и тогава имаме
| R=sR0 |
Едно нещо, което R не ни казва обаче, е колко бързо се променят нещата. Това е така, защото R не е скорост, тенп, няма времева рамка. Например, ако R = 2 за някакво заболяване, тогава знаем, че епидемията ще нарасне (защото >1), но не можем да кажем колко бързо. За заболявания като ХИВ или туберкулоза, при които може да изминат месеци или години, докато един човек зарази друг, дори R = 2 може да означава бавен растеж във времето. Въпреки това за грип или морбили, където инфекцията е много по-бърза, в дневна скала, R = 2 означава много бърз растеж.
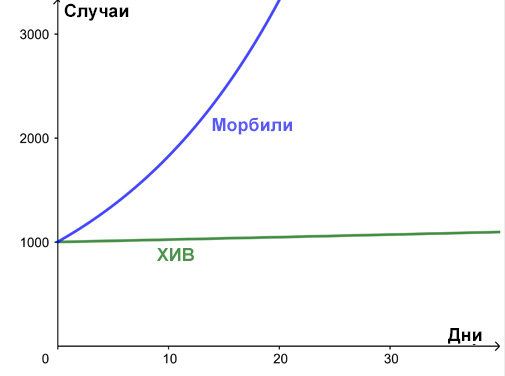
Ето две примерни криви за нарастване на инфекцията, и двете с коефициент на възпроизвеждане R =2. Разликата е времето между новите инфекции – няколко месеца за ХИВ, но само дни за морбили.
Какъв е темпът на растеж на епидемията?
Темпът на нарастване на случаите на заболяването е естествен начин да разберем колко бързо броят на инфекциите променя с всеки изминал ден. Растежът на случаите на заболяването се моделира с помощта на експоненциална крива:
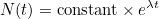 |
Тук N броя на случаите, който зависи от времето, t измерено в дни, и l ("ламбда") е темпът на нарастване на случаите на заболяването на ден. (Числото e е математическа константа, приблизително равна на 2,719 и тясно свързана с експоненциалния растеж)
За примерните криви по-горе, темпът на растеж за ХИВ е l =0,002 на ден, а за морбили е l =0,06 на ден. Това води до изключително различни резултати през следващия месец, въпреки че и двете заболявания в този пример имат еднакво репродуктивно число. Можете да използвате интерактивността по-долу, за да проучите как нарастването на случаите на заболяването се променя за различни темпове на растеж (използвайте плъзгача, за да промените стойността на l ).
С тревога наблюдавахме как до преди седмици всеки ден се отчитаха все повече нови случаи на заразяване с COVID-19 и нови смъртни случаи, а сега наблюдаваме как намаляват напоследък. Ако темпът на растеж е положителен, броят на новите случаи всеки ден се увеличава, ако темпът на растеж е 0, броят на новите случаи остава постоянен. Това, което е необходимо, за да се държи епидемията под контрол, е темпът на растеж да бъде отрицателен, а оттам и броят на новите случаи да намалява. Ако броят на новите случаи е намалял с 3% от вчера, тогава темпът на растеж е приблизително l = -0,03 на ден. (Това не е точно еквивалентно, но е добро приближение за типичните стойности на l. Темпът на растеж всъщност работи като сложна лихва)
Обратно, за малки стойности на l (напр. l =0.01 ), стойността на ламбда се доближава до процентния растеж в случаите на ден: l =0.01 означава, че случаите ще се увеличават с около 1% на ден. Въпреки това, за по-големи стойности на ламбда (напр. l =0.35 ) това приближение вече не е точно. В този случай процентното нарастване от един ден на следващия е el -1 (напр. за l =0.35 това е 0.42). (За по-подробно обяснение на връзката между темпа на растеж и процентния растеж на ден прочетете "Как да изчислим времето, за което се удвояват случаите на Омикрон".)
Кое е по-добро: R или темпът на растеж на случаите?
Както репродуктивното число R, така и скоростта на растеж l, са валидни мерки за разбиране на нарастването на заболяването. Всеки от тях има своя област на употреба, както е посочено по-долу:
| Коефициент на възпроизвеждане: R | Темп на растеж на ден: l |
|---|---|
|
R е по-естествено за разбиране на силата на интервенцията, необходима за спиране на епидемията, по-добро за планиране на мерките за контрол. Например:
|
Скоростта на нарастването е по-удобна да разберем как случаите се променят с течение на времето. Например
|
| R > 1 експоненциален растеж R = 1 плато R < 1 експоненциален спад |
l > 0 експоненциален растеж |
| R е съотношение на случаите по поколение на инфекция. Това не е темп, скорост, градиент, т.е. няма времева рамка. | Темпът на растеж l е скоростта на нарастването на случаите, която обикновено се дава в дни за COVID-19. |
| R изобщо не е лесно да се измери на практика, но може да се определи с помощта на модели, ако са известни времевите скали на инфекция. По принцип може да се оцени чрез подробни епидемиологични данни кой точно от кого е получил инфекция, но това обикновено не е осъществимо в типични условия. | Темпът на растеж l е сравнително лесен за оценка от данни от времеви серии за случаи на заразяване или смъртни случаи (но за малки числа). Простият подход е да се намери градиента на регистрираните случаи. По-усъвършенстваните подходи, които могат да вземат предвид променящия се във времето темп на растеж или хетерогенността на популацията, отново включват подходящи модели на епидемията. |
Както ефективното репродукционно число, така и темпът на растеж са особено трудни за оценка, когато броят на случаите е малък, например ако честотата на заболяването е много ниска или ако общността, която се проучва, има много малко население. В този случай ежедневните колебания могат лесно да объркат основните модели на заболяването, така че ще има по-голяма несигурност относно темпа на растеж и с по-широки интервали на доверие.
Как се стига от R до темпа на растеж и обратно?
Точната връзка между R и скоростта на растеж не е ясна: тя трябва да вземе предвид времето на всяка инфекция до следващата. Грубо приближение е
| R = e lT |
където T е средното време на генериране - времето от една инфекция до следващата.
Всичко това предполага, че мерките за контрол и броят на хората, податливи на заболяването, не се променят твърде бързо.
Ако сте изучавали висша математика, формулата горе може да се представи и по-прецизен вариант.
Следвайки един заразен човек, обозначете времето му от момента на заразяването с t (в дни). Такива хора заразяват средно R други хора. За всеки от тях времето на заразяване се разпределя с функцията на плътността на вероятностите ƒ (t). Тогава (само за студенти по математика) R и l са свързани както следва:
и да, това е много тясно свързано с преобразуване/трансформация на Лаплас.
За специфични разпределения на интервала на генериране на заразяванията, например гама разпределение, това понякога може да бъде опростено. Ако приемем времето на интервала на генериране на заразяванията за константа, да речем, T се опростява R = elT, но това е доста грубо приближение за много инфекциозни заболявания на практика.
Всъщност ƒ (t) зависи от различни неща, включително биологични неща като инкубационния период и от социални фактори като това дали заразените все още се смесват с други, когато имат симптоми или се самоизолират.
Авторът на тази статия е Джулия Гог (Julia Gog), професор по математическа биология в Университета в Кеймбридж, като част от сътрудничество JUNIPER, съвместен университетски консорциум за моделиране на пандемията и реакцията на епидемии. JUNIPER включва учени от университетите в Кеймбридж, Уоруик, Бристол, Ексетър, Оксфорд, Манчестър и Ланкастър, които използват набор от математически и статистически техники за справяне с неотложния въпрос за контрола на COVID-19. Можете да видите повече съдържание, произведено от JUNIPER тук.
Гог е член и на SPI-M, група за моделиране, която предава резултатите си на Научната консултативна група за извънредни ситуации (SAGE) и на управителния комитет на национален консорциум, ръководен от Кралското общество, за справяне с пандемията от COVID-19.
Справка: How generation intervals shape the relationship between growth rates and reproductive numbers
J Wallinga and M Lipsitch
Published:28 November 2006 https://doi.org/10.1098/rspb.2006.3754
Източник: The growth rate of COVID-19, Plus magazine, University of Cambridge
под редакцията на Рейчъл Томас (Rachel Thomas) и Мариан Фрайбергер (Marianne Freiberger).























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?
Nikor
На 30 септември 1928 е открит пеницилинът
Прост Човек
Ново обяснение за гигантските експлодиращи кратери в Сибир