

Много хора се питат, а някои дори се възмущават, защо математици обясняват хода на пандемията. Те вероятно ще се изненадат колко много математика има в описанието и прогнозата на разпространението на едно инфекциозно заболяване, защото законите на природата на експоненциалния растеж са едни и същи - от размножаването на насекомите до това, как парите (или дългът) във вашата банкова сметка нарастват чрез сложна лихва.
С тази статия започваме цикъл "Математика на пандемията" от материали, които обясняват основните математически термини и концепции, които описват развитието на пандемията - събитие, засегнало от вече две години живота на всички и като че ли не иска да си тръгва, независимо от нашите желания.
Две неща, за които много от нас ще са чували през последните няколко седмици, са концепцията за имунитет на стадото и числото, наречено R0 (което хората казват като „R нула“).
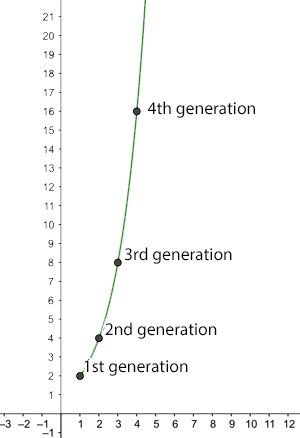 Броят на новите инфекции след n поколения за R0 =2 Броят на новите инфекции след n поколения за R0 =2 |
Основното репродуктивно число
Като се има предвид инфекциозна болест, като COVID-19, R0 е основното репродуктивно число на болестта: средният брой хора, които зарàзен човек заразява, като се има предвид, че всеки в популацията е податлив на болестта. За сезонните щамове на грипа то е между 0,9 и 2,1. А за морбили е невероятните 12 до 18. За в момента то се оценява между 2 и 2,5.
След 20 месеца на пандемия COVID-19 R0 се превърна в условна концепция, защото не остана незасегната популация. R0 е около 3 за оригиналния вирус от див тип, в сравнение с около 5 за Делта и доста повече за Омикрон - между 6 и 15.
Можете да видите как достатъчно голям R0 води до бързо разпространение на болестта. Например, ако R0 е равно на 2, тогава едно заразено лице генерира следното нарастване на броя на нови инфекции:
1-во поколение: 2 нови инфекции
2-ро поколение: 4 нови инфекции
3-то поколение: 8 нови инфекции
4-то поколение: 16 нови инфекции.
Като цяло има 2n нови инфекции в n кръга на новите инфекции. Ако приемем, че човек е зарàзен само за една седмица, при този темп цялото население на света (7,8 милиарда) ще бъде заразено след малко повече от 32 седмици.
Когато основното число на възпроизвеждане R0 е по-малко от 1, се появява съвсем различна картина. Като илюстрация, представете си, че имаме R0 =0,5 Сега очевидно, заразен човек не може да зарази половината човек, но не забравяйте, че това е средна стойност: това означава, че може да се предположи, че 10 души могат да продължат да заразят 5 други, или че Може да се предположи, че 100 души ще заразят 50 други. Както и преди, нека приемем, че има 1 заразен човек за начало, тогава броят на новите инфекции се държи по следния начин:
1-во поколение: 0.5 нови инфекции
2-ро поколение: 0.25 нови инфекции
3-то поколение: 0.125 нови инфекции
4-то поколение: 0.0625 нови инфекции.
Като цяло имаме (0.5)n нови инфекции за n кръга от инфекции. Този брой става все по-малък с увеличаването на броя n на поколенията. Задънена улица за болестта.
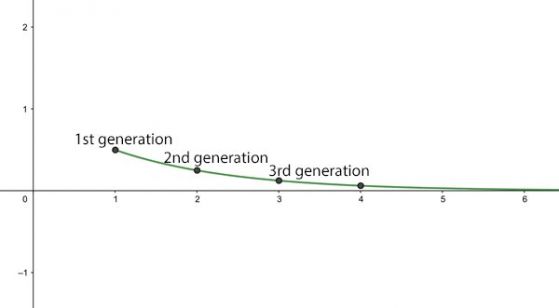
Средният брой нови инфекции след n поколения за R0 =0,5.
Ами ако R0 = 1? В този случай болестта ще бъде ендемична: винаги присъства в популацията, но не и епидемия.
Ефективно репродуктивно число
И така, като се има предвид, че R0 коефициентът на морбили или някои щамове на сезонен грип е по-голям от 1, как така целият свят не е бил заразен с тези болести отдавна? Причината е, че R0 е средният брой хора, които заразен човек заразява, ако всеки в популацията е податлив. Това може да се случи в реалния живот, ако някой, който се е заразил с болест другаде, навлезе в част от света, където болестта никога не е била виждана преди, така че хората нямат имунитет и няма ваксина за защита тях. Един R0 от 2 тогава означава, че в началото броят на заразените ще нараства неимоверно, както е описано по-горе.
Въпреки това, след като човек се възстанови от болестта, той придобие някакъв имунитет, това означава, че след известно време вече няма да имаме работа с напълно податлива популация. Всъщност може да има други причини, поради които някои хора от популацията не са податливи: те може да са имунизирани по други причини, или ако има ваксина, може да са я получили, или може да са изолирани от останалата част от населението.
В повечето ситуации от реалния живот трябва да разглеждаме ефективното репродуктивно число на болестта, понякога обозначаван с R: средният брой, който заразеното лице продължава да заразява в популация, където някои хора са имунизирани (или са налице някои други интервенции). Разбира се R0 и R са свързани. Пишем s за дела от населението, което е податливо на заразяване, и тогава имаме
| R=sR0 |
Като пример, ако само половината от населението е податливо, тогава имаме s=0.5 и съответно R=0,5R0. В този случай, ако R0 е по-малко или равно на 2, тогава R е по-малко или равно на 1 и болестта няма да се превърне в епидемия. Идеалната цел на всяка интервенция, било то ваксинация или социално дистанциране, е да се намали ефективното репродуктивно число до под 1.
Стаден имунитет
Какво общо има всичко това със стадния (или колективния, но се наложи термина "стаден") имунитет? Общата идея зад стадния имунитет е, че в популация, където много хора са имунизирани, болестта не може да се задържи и да прерасне в епидемия, като по този начин защитава хората, които не са имунизирани. Популацията (може би за съжаление се нарича "стадо") защитава уязвимите индивиди.
И така, колко хора в една популация трябва да имат имунитет, за да имат стаден имунитет? Представете си, че болестта има основно репродуктивно число R0 , което е по-голямо от 1, така че е налице заплаха от епидемия. Както видяхме, ако ефективното репродуктивно число R е по-малко от 1, тогава болестта в крайна сметка ще изчезне. Така че, за да постигнем стаден имунитет, трябва по някакъв начин да намалим ефективния репродуктивен брой R под 1. Тъй като R=sR0, къде s е делът на популацията, която е възприемчива, трябва
| s.R0 < 1 |
Пренареждане, това дава
| s < 1/R0 |
С други думи, трябва да доведем дела на уязвимите хора в популацията до под 1/R0. Колко хора трябва да имат имунитет, за да постигнем това? Ако делът на податливите хора е s, тогава делът на хората, които не са податливи, с други думи имунизирани, е 1 - s. Сега
| s < 1/R0 |
означава
| 1 - s > 1 - 1/R0 |
Така че, за да постигнем стаден имунитет, трябва да се уверим, че поне част от 1- 1/R0 населението е имунизирано. За R0=2.5, по-високият край на оценките за COVID-19, това означава, че трябва 1-1/2.5=0.6 от популацията да има имунитет. Това означава поне 60%.
За варианта Делта, за който R0 = 5.1, означава, че трябва да имаме 1-1/5.1≈0.80 като част от населението с имунитет или поне 80%.
Това означава, че за ваксина, която е 100% ефективна, така че всеки, който я получи, е имунизиран, трябва 80% от хората трябва да бъдат ваксинирани, за да се постигне стаден имунитет. Но няма ваксина, която е 100% ефективна.
Ако дадена ваксина има ефективност от x %, това означава, че само x % от хората, които я получават, са имунизирани. За да постигнем стаден имунитет, трябва x % от дела на хората, които са ваксинирани, да се преобразува в пропорция от поне 1-1/ R 0 от популацията. С други думи,
къде P е делът на ваксинираните. Това дава
Заместването за варианта Делта, за който R0 = 5.1 дава
| P ≥ 80/x |
Следователно за ваксина, която е 95% ефективна, ние трябва да ваксинираме поне част от
| 80/95 = 0.84 |
души, което се равнява на 84%.
Тази формула обаче показва отчайващата констатация, че за ваксина, която е 80% ефективна трябва 100% от населенито трябва да е имунизирано, а по-ниско ефективните ваксини са безсилни да спрат варианта Делта, да не говорим за още по-трансмисивния вариант Омикрон.
Какви са реалните данни? Ефективността на ваксината на Moderna срещу инфекция с Делта вариант намалява с 94,1% (90,5% до 96,3%) 14-60 дни след ваксинацията до 80,0% (70,2% до 86,6%) 151-180 дни след ваксинацията по данни на BMJ.
Разбира се, надбягването на новите мутации и ваксините ще продължи. Трябва и да се отбележи, че до тук говорихме за идеалния случай на защита от заразяване и стаден имунитет. Ваксините все още дават добра защита от тежко заболяване, хоспитализация и смърт.
Имунитетът може да бъде постигнат и естествено, като хората се разболеят, но новите варианти както снижават ефективността на ваксините, с още по-голям успех заобикалят и естествения имунитет, който се придобива и на още по-висока цена. Твърде много хора умират от COVID-19, не можем просто да оставим болестта да обхване населението, уверени, че повече инфекции означават повече имунитет - на което не може да се разчита предвид немалкото случаи на повторно заболяване.
И така, какво да правим в този най-лош сценарий?
При нисък процент на ваксинацията една от възможностите е да се остане в изолация. Другата е да влезем в периодични локдауни, за да задържим последователните пикове на епидемията под критичния капацитет на системата за здравеопазване.
Истината е, че в този момент никой не знае какво точно ще се случи в бъдеще. Най-обоснованите ни предположения идват от математически модели, които се опитват да предскажат хода на пандемията. Повече за тези модели може да научите в статията: "Как се моделира математически епидемията?".
Като цяло изчисленията по-горе също изпращат важно послание за ваксинацията: тя не само защитава индивида, който е ваксиниран срещу болестта, но и тези хора, които по някаква причина няма да бъдат ваксинирани и следователно ще са уязвими. Ваксинацията не е само за вас, тя е за цялото "стадо"!
В тази статия са използвани два материала на сайта "Plus magazine" на Университета в Кеймбридж:
- "Maths in a minute: "R nought" and herd immunity" , базиран на глава от книгата Understanding numbers (Разбиране на числата ) от редакторите на Plus magazine Рейчъл Томас (Rachel Thomas) и Мариан Фрайбергер (Marianne Freiberger).
- "Since herd immunity will protect us all, why do I need to get vaccinated?", Мат Кийлинг (Matt Keeling) професор в Университета на Уоруик и Сам Мур (Sam Moore), постдокторант в Университета на Уоруик, под редакцията на Рейчъл Томас и Мариан Фрайбергер




















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
Nikor
На 30 септември 1928 е открит пеницилинът
Прост Човек
Ново обяснение за гигантските експлодиращи кратери в Сибир
dolivo
Климатичният скептицизъм – най-скъпата лъжа на нашето време
helper68
Използването на смартфон в тоалетната е свързано с 46% по-висок риск от хемороиди