

–ē–ī–ł–Ĺ –ĺ—ā –Ĺ–į–Ļ-–ľ–ĺ—Č–Ĺ–ł—ā–Ķ –Ĺ–į—á–ł–Ĺ–ł –ī–į —Ā–Ķ –ł–∑–ĺ–Ī—Ä–į–∑—Ź–≤–į—ā —Ą—Ä–į–ļ—ā–į–Ľ–ł, –ľ–Ķ—ā–ĺ–ī –Ĺ–į–ľ–Ķ—Ä–ł–Ľ –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ł –≤ –ī—Ä—É–≥–ł –ĺ–Ī–Ľ–į—Ā—ā–ł –Ķ –ľ–Ķ—ā–ĺ–ī–į –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–ł—ā–Ķ –ł—ā–Ķ—Ä–į—ā–ł–≤–Ĺ–ł —Ą—É–Ĺ–ļ—Ü–ł–ł (IFS).
IFS –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—ā —Ā–ł—Ā—ā–Ķ–ľ–į –ĺ—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –ļ–Ľ–į—Ā —Ą—É–Ĺ–ļ—Ü–ł–ł, –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į—Č–ł –Ķ–ī–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ–ľ–Ķ—Ä–Ĺ–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –≤ –ī—Ä—É–≥–ĺ. –Ě–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–į—ā–į IFS —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –∑–į —Ä–į–≤–Ĺ–ł–Ĺ–į:
x' = x * –į + y * b + e
y' = x * c + y * d + f
–Ę–į–∑–ł —Ā–ł—Ā—ā–Ķ–ľ–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ł –ľ–į—ā—Ä–ł—á–Ĺ–ĺ –Ņ–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ:
 
–ź—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł
–ü–ĺ–ī –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł —Ā–Ķ —Ä–į–∑–Ī–ł—Ä–į—ā —ā–į–ļ–ł–≤–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, –Ņ—Ä–ł –ļ–ĺ–ł—ā–ĺ —É—Ā–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ł—ā–Ķ –Ņ—Ä–į–≤–ł –ĺ—Ā—ā–į–≤–į—ā —É—Ā–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ł. ¬†–ü—Ä–ł —ā–į–ļ–ł–≤–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –Ĺ–Ķ –Ķ –∑–į–ī—ä–Ľ–∂–ł—ā–Ķ–Ľ–Ĺ–ĺ –ī–į —Ā–Ķ –∑–į–Ņ–į–∑—Ź—ā —ä–≥–Ľ–ł—ā–Ķ –ľ–Ķ–∂–ī—É –Ņ—Ä–į–≤–ł—ā–Ķ –ł–Ľ–ł —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—ā–į –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–ł—ā–Ķ, –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ —Ā–Ķ –∑–į–Ņ–į–∑–≤–į—ā —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź—ā–į –ľ–Ķ–∂–ī—É —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—ā–į –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–ł, –Ľ–Ķ–∂–į—Č–ł –Ĺ–į –Ķ–ī–Ĺ–į –Ņ—Ä–į–≤–į. –ź—Ą–ł–Ĺ–Ĺ–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł —Ā–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł - —ā.–Ķ. –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł—ā–Ķ —Ā—ā–į–≤–į –Ņ–ĺ –Ľ–ł–Ĺ–Ķ–Ķ–Ĺ –∑–į–ļ–ĺ–Ĺ. –Ę–Ķ –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –≤–ļ–Ľ—é—á–≤–į—ā –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ, —Ä–ĺ—ā–į—Ü–ł—Ź, —ā—Ä–į–Ĺ—Ā–Ľ–į—Ü–ł—Ź (—É—Ā–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ĺ –Ņ—Ä–Ķ–Ĺ–į—Ā—Ź–Ĺ–Ķ), –ĺ–≥–Ľ–Ķ–ī–į–Ľ–Ĺ–ĺ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ.

–Ě–į–ľ–į–Ľ—Ź–≤–į—Č–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ–ľ–į—Ü–ł–ł. –ź—ā—Ä–į–ļ—ā–ĺ—Ä–ł
–ú–į—Č–į–Ī–ł—Ä–į—Č–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł —Ā–į –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –Ĺ–į–ľ–į–Ľ—Ź–≤–į—Č–ł, —ā.–Ķ. —ā–ĺ—á–ļ–ł—ā–Ķ —Č–Ķ —Ā–Ķ —Ā–Ī–Ľ–ł–∂–į–≤–į—ā –ł —Ą–ĺ—Ä–ľ–ł—ā–Ķ —Č–Ķ —Ā—ā–į–≤–į—ā –Ņ–ĺ-–ľ–į–Ľ–ļ–ł. –Ę–į–ļ–į –Ķ–ī–ł–Ĺ IFS —Ą—Ä–į–ļ—ā–į–Ľ —Č–Ķ –Ķ —Ā—ä—Ā—ā–į–≤–Ķ–Ĺ –ĺ—ā –Ņ–ĺ-–ľ–į–Ľ–ļ–ł –ļ–ĺ–Ņ–ł—Ź –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł, –ļ–ĺ–ł—ā–ĺ –ĺ—ā —Ā–≤–ĺ—Ź —Ā—ā—Ä–į–Ĺ–į, —Č–Ķ —Ā–Ķ —Ā—ä—Ā—ā–ĺ—Ź—ā –ĺ—ā –ļ–ĺ–Ņ–ł—Ź –Ĺ–į —Ā–Ķ–Ī–Ķ —Ā–ł –ł —ā.–Ĺ. –ł —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –Ĺ–į –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–į —Č–Ķ –ĺ—Ā–ł–≥—É—Ä–ł –Ĺ–Ķ–≥–ĺ–≤–ĺ—ā–ĺ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ - —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ—ā–ĺ.
–ó–į¬†—ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź, –ļ–ĺ—Ź—ā–ĺ –Ĺ–į–ľ–į–Ľ—Ź–≤–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–ł—ā–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 1 –Ņ—ä—ā —ā.–Ķ. –ļ–ĺ—Ą–ł—Ü–ł–Ķ–Ĺ—ā—ä—ā –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ķ –Ņ–ĺ-–ľ–į–Ľ—ä–ļ –ĺ—ā 1, —Ā—ä–≥–Ľ–į—Ā–Ĺ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ĺ–į –Ď–į–Ĺ–į—Ö, –≤ –Ĺ–į–ľ–į–Ľ–Ķ–Ĺ–ĺ—ā–ĺ –ļ–ĺ–Ņ–ł–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ĺ–Ķ–Ņ–ĺ–ī–≤–ł–∂–Ĺ–į —ā–ĺ—á–ļ–į, –ł —ā–ĺ —Ā–į–ľ–ĺ –Ķ–ī–Ĺ–į. –Ę–į–∑–ł —ā–ĺ—á–ļ–į —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ĺ—Č–Ķ –į—ā—Ä–į–ļ—ā–ĺ—Ä.–Ę–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ķ –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į –≤ —á–Ķ—Ā—ā –Ĺ–į –Ņ–ĺ–Ľ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –°—ā–Ķ—Ą–į–Ĺ –Ď–į–Ĺ–į—Ö, —É—Ā—ā–į–Ĺ–ĺ–≤–ł–Ľ –ł –ī–ĺ–ļ–į–∑–į–Ľ —ā–ĺ–≤–į —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ –Ņ—Ä–Ķ–∑ 1922 –≥. –°–ł—Ā—ā–Ķ–ľ–ł—ā–Ķ –ł—ā–Ķ—Ä–į—ā–ł–≤–Ĺ–ł —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā–į –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –Ņ—Ä–ł–Ľ–į–≥–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł —ā–Ķ–ĺ—Ä–ł—Ź.
Iterated Systems Inc
–Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ķ —Ä–į–∑—Ä–į–Ī–ĺ—ā–Ķ–Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ĺ—ā –Ē–∂–ĺ–Ĺ –•—ä—ā—á–ł–Ĺ—Ā—ä–Ĺ (John Hutchinson), –Ĺ–ĺ –ľ–Ķ—ā–ĺ–ī—ä—ā —Ā—ā–į–≤–į –Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ķ–Ĺ, —Ā–Ľ–Ķ–ī –ļ–į—ā–ĺ –Ņ—Ä–Ķ–∑ 1988 –≥. –Ī—Ä–ł—ā–į–Ĺ—Ā–ļ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł (Michael Barnsley) –≤–ł–∂–ī–į –≤ —ā–ĺ–∑–ł –ľ–Ķ—ā–ĺ–ī –Ņ–ĺ—ā–Ķ–Ĺ—Ü–ł–į–Ľ –∑–į —Ā–≤–ł–≤–į–Ĺ–Ķ(–į—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–Ķ) –ł —Ā—ä—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į –≥—Ä–į—Ą–ł—á–Ĺ–į –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź. –ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł –ł –ź–Ľ–į–Ĺ –°–Ľ–ĺ—É–Ĺ (Alan Sloan) –ĺ—Ā–Ĺ–ĺ–≤–į–≤–į—ā –ļ–ĺ—Ä–Ņ–ĺ—Ä–į—Ü–ł—Ź—ā–į¬†Iterated Systems Inc. –Ņ—Ä–Ķ–∑ 1987 –≥., –ļ–ĺ—Ź—ā–ĺ –Ņ–ĺ–Ľ—É—á–į–≤–į –Ĺ–į–ī 20 –Ņ–į—ā–Ķ–Ĺ—ā–į, —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–į—ā–į –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ź.
–ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł –Ĺ–į—Ä–Ķ–ļ—ä–Ľ —Ā–≤–ĺ—Ź –ľ–Ķ—ā–ĺ–ī –ľ–Ķ—ā–ĺ–ī –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ĺ—ā–ĺ –į—Ä—Ö–ł–≤–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź—ā–į –ł —Ā—ä–∑–ī–į–Ľ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –ļ–ĺ–Ļ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ä–į –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź—ā–į 500-1000 –Ņ—ä—ā–ł. –ú–Ķ—ā–ĺ–ī—ä—ā –Ķ –Ĺ–į–Ļ-–Ņ–ĺ–ī—Ö–ĺ–ī—Ź—Č –∑–į —ā–Ķ–ļ—Ā—ā—É—Ä–ł –ł –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –∑–į—Ä–į–ī–ł —Ą–į–ļ—ā–į, —á–Ķ —á–į—Ā—ā–ł –ĺ—ā –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —á–Ķ—Ā—ā–ĺ –Ņ—Ä–ł–Ľ–ł—á–į—ā –Ĺ–į –ī—Ä—É–≥–ł —á–į—Ā—ā–ł –ĺ—ā —Ā—ä—Č–ĺ—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ.
–ź—Ā–Ņ–ł—Ä–į–Ĺ—ā—ä—ā –Ĺ–į –Ď–į—Ä–Ĺ—Ā–Ľ–ł, –ź—Ä–Ĺ–ĺ –Ė–į–ļ–Ķ–Ĺ (Arnaud Jacquin) —Ä–Ķ–į–Ľ–ł–∑–ł—Ä–į –Ņ—ä—Ä–≤–ł—Ź –į–≤—ā–ĺ–ľ–į—ā–ł—á–Ķ–Ĺ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –ļ–ĺ–Ļ—ā–ĺ —Ä–į–∑–ī–Ķ–Ľ—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ĺ—ā–ī–Ķ–Ľ–Ĺ–ł –Ī–Ľ–ĺ–ļ–ĺ–≤–Ķ –ĺ–Ī–Ľ–į—Ā—ā–ł –ł–Ľ–ł –ī–ĺ–ľ–Ķ–Ļ–Ĺ–ł(domain blocks) –ł –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į –Ņ–ĺ-–ľ–į–Ľ–ļ–ł –Ī–Ľ–ĺ–ļ–ĺ–≤–Ķ (range subimage blocks).
–ė–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź—ā–į –∑–į –Ķ–ī–Ĺ–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź —Ā–Ķ —Ā—ä–Ī–ł—Ä–į –Ĺ–į –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –Ī–į–Ļ—ā–į, –ī–ĺ–ļ–į—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ, —Ā—ä–∑–ī–į–ī–Ķ–Ĺ–ĺ —Ā IFS, –ľ–ĺ–∂–Ķ –ī–į –ĺ—ā–Ĺ–Ķ–ľ–Ķ –ł –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ľ–Ķ–≥–į–Ī–į–Ļ—ā–į.
–°—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ä–į–Ĺ–Ķ –Ķ –ľ–Ĺ–ĺ–≥–ĺ –≤–ł—Ā–ĺ–ļ–į, –Ĺ–ĺ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł—Ź —Ö–į—Ä–ī—É–Ķ—Ä –Ĺ–Ķ –Ķ –Ī–ł–Ľ –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –ľ–ĺ—Č–Ķ–Ĺ –ĺ—ā —ā–ĺ–≤–į –≤—Ä–Ķ–ľ–Ķ –∑–į –ī–į –ľ–ĺ–∂–Ķ –ľ–Ķ—ā–ĺ–ī—ä—ā –ī–į –Ī—ä–ī–Ķ —ą–ł—Ä–ĺ–ļ–ĺ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä 15 —á–į—Ā–į —Ā–į –Ī–ł–Ľ–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł –∑–į –ī–į —Ā–Ķ –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ä–į –Ķ–ī–Ĺ–į –ľ–ł–Ĺ—É—ā–į –≤–ł–ī–Ķ–ĺ.
–í –ľ–ĺ–ľ–Ķ–Ĺ—ā–į –ī–≤–Ķ —Ą–ł—Ä–ľ–ł, Total Multimedia Inc. –ł Dimension —ā–≤—ä—Ä–ī—Ź—ā, —á–Ķ –Ņ—Ä–ł—ā–Ķ–∂–į–≤–į—ā –ł–∑–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ł –Ņ—Ä–į–≤–į –∑–į —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –ł—ā–Ķ—Ä–į—ā–ł–≤–Ĺ–į –≤–ł–ī–Ķ–ĺ –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ź, –Ĺ–ĺ –Ĺ—Ź–ľ–į –≤—Ā–Ķ –ĺ—Č–Ķ —Ä–į–Ī–ĺ—ā–Ķ—Č –Ņ—Ä–ĺ–ī—É–ļ—ā.
–ě–Ņ–ł—Ā–į–Ĺ–ł–Ķ
–Ě–į–ļ—Ä–į—ā–ļ–ĺ –ľ–Ķ—ā–ĺ–ī—ä—ā –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ–Ņ–ł—ą–Ķ —ā–į–ļ–į: –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —Ā–Ķ –ļ–ĺ–ī–ł—Ä–į —Ā –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ–Ņ—Ä–ĺ—Ā—ā–ł –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, —ā.–Ķ. —Ā –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į —ā–Ķ–∑–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł.
–Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –∑–į–ļ–ĺ–ī–ł—Ä–į–Ļ–ļ–ł –Ĺ—Ź–ļ–į–ļ–≤–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —Ā –ī–≤–Ķ –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, –Ĺ–ł–Ķ –Ķ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–ľ–Ķ —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į 12-—ā–Ķ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į. –ź–ļ–ĺ —Ā–Ķ –∑–į–ī–į–ī–Ķ –Ĺ—Ź–ļ–į–ļ–≤–į –Ĺ–į—á–į–Ľ–Ĺ–į —ā–ĺ—á–ļ–į (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä
–Ě–ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –≤ —ā–ĺ–≤–į, —á–Ķ –Ņ–ĺ–Ĺ—Ź–ļ–ĺ–≥–į –Ķ —ā—Ä—É–ī–Ĺ–ĺ –ī–į —Ā–Ķ –Ĺ–į–ľ–Ķ—Ä—Ź—ā –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į IFS.
–ö–į—ā–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–Ķ –Ĺ–į IFS –∑–į –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł, –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł –ļ—Ä–ł–≤–ł. –©–Ķ –ĺ—ā–ī–Ķ–Ľ–ł–ľ –≤ —ā–Ķ—Ö–Ĺ–ł—ā–Ķ —Ā—ā—Ä—É–ļ—ā—É—Ä–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł—ā–Ķ —á–į—Ā—ā–ł –ł –∑–į –≤—Ā—Ź–ļ–į –ĺ—ā —ā—Ź—Ö —Č–Ķ –ł–∑—á–ł—Ā–Ľ–ł–ľ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į –į—Ą–ł–Ĺ–Ĺ–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ. –í –į—Ą–ł–Ĺ–Ĺ–ł—Ź –ļ–ĺ–Ľ–į–∂ —Č–Ķ –Ī—ä–ī–į—ā –≤–ļ–Ľ—é—á–Ķ–Ĺ–ł —ā–ĺ–Ľ–ļ–ĺ–≤–į –į—Ą–ł–Ĺ–Ĺ–ł –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź, –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ —Ā–į —á–į—Ā—ā–ł—ā–Ķ, –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –Ĺ–į —Ü—Ź–Ľ–ĺ—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ.
–Ē—Ä–į–ļ–ĺ–Ĺ –Ĺ–į –•–į—Ä—ā–Ķ—Ä-–•–Ķ–Ļ—ā—É–Ķ–Ľ
| –Ē–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ IFS –∑–į "–ī—Ä–į–ļ–ĺ–Ĺ–į" –Ĺ–į –•–į—Ä—ā–Ķ—Ä-–•–Ķ–Ļ—ā—É–Ķ–Ľ. –ó–į —ā–į–∑–ł —Ü–Ķ–Ľ –ī–į —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ –Ņ—ä—Ä–≤–ĺ—ā–ĺ –Ņ–ĺ–ļ–ĺ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į —ā–ĺ–∑–ł —Ą—Ä–į–ļ—ā–į–Ľ –≤ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į—ā–į –ľ—Ä–Ķ–∂–į –Ĺ–į –ī–ł—Ā–Ņ–Ľ–Ķ—Ź 640 x 350 . –Ē–į –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ —ā–ĺ—á–ļ–ł—ā–Ķ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į—ā–į –Ĺ–į—á—É–Ņ–Ķ–Ĺ–į –Ľ–ł–Ĺ–ł—Ź A, B, C. –ü–ĺ –Ņ—Ä–į–≤–ł–Ľ–į—ā–į –∑–į –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ, —ā–ĺ–∑–ł —Ą—Ä–į–ļ—ā–į–Ľ –ł–ľ–į –ī–≤–Ķ —á–į—Ā—ā–ł, –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –Ĺ–į —Ü—Ź–Ľ–ĺ—ā–ĺ - –Ĺ–į —Ā—Ö–Ķ–ľ–į—ā–į –≤–ī—Ź—Ā–Ĺ–ĺ —ā–ĺ–≤–į —Ā–į –Ĺ–į—á—É–Ņ–Ķ–Ĺ–ł—ā–Ķ –Ľ–ł–Ĺ–ł–ł ADB –ł BEC. –ó–Ĺ–į–Ķ–Ļ–ļ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł—ā–Ķ –Ĺ–į –ļ—Ä–į–ł—Č–į—ā–į –Ĺ–į —ā–Ķ–∑–ł –ĺ—ā—Ā–Ķ—á–ļ–ł, –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź—ā –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į –ī–≤–Ķ –į—Ą–ł–Ĺ–Ĺ–ł –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź, –Ņ—Ä–Ķ–≤—Ä—ä—Č–į—Č–ł –Ĺ–į—á—É–Ņ–Ķ–Ĺ–į—ā–į –Ľ–ł–Ĺ–ł—Ź ABC –≤ ADB –ł BEC: |  |
|||||||||||
| x' = -0.5*x -0.5*y + 490 y' = 0.5*x -0.5*y + 120 x' = 0.5*x -0.5*y + 340 y' = 0.5*x +0.5*y - 110 |
||||||||||||
–ö—Ä–ł–≤–į –Ĺ–į –ö–ĺ—Ö
–ü–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ĺ, –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ł–∑–≥—Ä–į–ī–ł IFS –∑–į –ļ—Ä–ł–≤–į—ā–į –Ĺ–į –ö–ĺ—Ö. –Ę–į–∑–ł –ļ—Ä–ł–≤–į –ł–ľ–į —á–Ķ—ā–ł—Ä–ł —á–į—Ā—ā–ł –ł —Ā–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł —Ā–į 4 —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł..

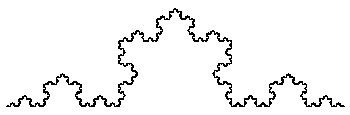
x' = 0.333*x + 13.333
y' = 0.333*y + 200
x' = 0.333*x + 413.333
y' = 0.333*y + 200
x' = 0.167*x + 0.289*y + 130
y' = -0.289*x + 0.167*y + 256
x' = 0.167*x - 0.289*y + 403
y' = 0.289*x + 0.167*y + 71
–°–Ľ–Ķ–ī 1000 –ł—ā–Ķ—Ä–į—Ü–ł–ł –ļ—Ä–ł–≤–į—ā–į –Ņ—Ä–ł–ī–ĺ–Ī–ł–≤–į –≤–ł–ī–į:¬†
 
–ü–į–Ņ—Ä–į—ā –Ĺ–į –Ď–į—Ä–Ĺ—Ā–Ľ–ł
–ē–ī–ł–Ĺ –ĺ—ā –Ĺ–į–Ļ-–≤–Ņ–Ķ—á–į—ā–Ľ—Ź–≤–į—Č–ł—ā–Ķ –Ņ—Ä–ł–ľ–Ķ—Ä–ł –∑–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į IFS, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ, –Ķ –ļ–ĺ–ī—ä—ā –Ĺ–į –Ņ–į–Ņ—Ä–į—ā, —Ä–į–∑—Ä–į–Ī–ĺ—ā–Ķ–Ĺ –ĺ—ā –Ď–į—Ä–Ĺ—Ā–Ľ–ł —Ā —á–Ķ—ā–ł—Ä–ł –Ĺ–į–ľ–į–Ľ—Ź–≤–į—Č–ł –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, –ļ–į—ā–ĺ —Ä–Ķ–∑—É–Ľ—ā–į—ā—ä—ā –Ņ–ĺ—Ä–į–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ĺ–į–Ņ–ĺ–ī–ĺ–Ī—Ź–≤–į –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł–Ķ—ā–ĺ.
–ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł –Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ľ —Ą—Ä–į–ļ—ā–į–Ľ–ł –∑–į –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į–Ĺ–Ķ –Ĺ–į —Ä–į–∑–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–į –≥–į–ľ–į –ĺ—ā —Ź–≤–Ľ–Ķ–Ĺ–ł—Ź –≤ –Ĺ–į—É–ļ–į—ā–į –ł —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł–ł—ā–Ķ, –Ĺ–ĺ –Ĺ–į–Ļ-–ł–∑—É–ľ–ł—ā–Ķ–Ľ–Ĺ–ł —Ā–į —Ä–į—Ā—ā–ł—ā–Ķ–Ľ–Ĺ–ł—ā–Ķ —Ā—ā—Ä—É–ļ—ā—É—Ä–ł.¬†–ě–Ņ–ł—ā—ä—ā –ľ—É –ī–į –ł–ľ–ł—ā–ł—Ä–į –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į —Ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ľ–ĺ–ī–Ķ–Ľ–ł¬†—Ā—ā–į–≤–į –ł–∑—ā–ĺ—á–Ĺ–ł–ļ –Ĺ–į –≤–ī—ä—Ö–Ĺ–ĺ–≤–Ķ–Ĺ–ł–Ķ –∑–į –ľ–Ĺ–ĺ–∑–ł–Ĺ–į —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł.
–ö–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –∑–į –ł–∑–≥—Ä–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ–į–Ņ—Ä–į—ā —Ā–į –≤ —Ā–Ľ–Ķ–ī–Ĺ–į—ā–į —ā–į–Ī–Ľ–ł—Ü–į:
| a | b | c | d | e | f | p | –ē–Ľ–Ķ–ľ–Ķ–Ĺ—ā |  |
| 0 | 0 | 0 | 0.16 | 0 | 0 | 0.01 | –°—ā—ä–Ī–Ľ–ĺ | |
| 0.85 | 0.04 | -0.04 | 0.85 | 0 | 1.6 | 0.85 | –†–Ķ–ī–ł—Ü–ł –ľ–į–Ľ–ļ–ł –Ľ–ł—Ā—ā–Ķ–Ĺ—Ü–į | |
| 0.2 | -0.26 | 0.23 | 0.22 | 0 | 1.6 | 0.07 | –Ě–į–Ļ-–≥–ĺ–Ľ—Ź–ľ–ĺ –Ľ—Ź–≤–į –Ľ–ł—Ā—ā–ĺ | |
| -0.15 | 0.28 | 0.26 | 0.24 | 0 | 0.44 | 0.07 | –Ě–į–Ļ-–≥–ĺ–Ľ—Ź–ľ–ĺ –ī—Ź—Ā–Ĺ–į –Ľ–ł—Ā—ā–ĺ |
–í —ā–į–Ī–Ľ–ł—Ü–į—ā–į, –ļ–ĺ–Ľ–ĺ–Ĺ–ł—ā–Ķ "–į" –ī–ĺ "–Ķ" —Ā–į –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ, –į¬†"—Ä" –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā—ä—ā –Ĺ–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā –∑–į –≤—Ā—Ź–ļ–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź, —É–Ņ—Ä–į–≤–Ľ—Ź–≤–į—Č–į –≤–ĺ–ī–Ķ—Č –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā –Ĺ–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ĺ–Ī–Ķ–ļ—ā–į.
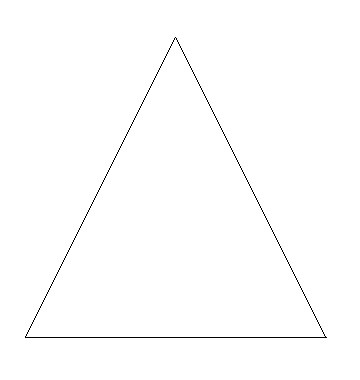
–Ě–į—á–į–Ľ–Ĺ–į—ā–į —Ą–ĺ—Ä–ľ–į –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į
–ź–ļ–ĺ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź—ā–į –Ķ –Ĺ–į–ľ–į–Ľ—Ź–≤–į—Č–į, —ā—Ź —Č–Ķ —Ā–Ī–Ľ–ł–∂–į–≤–į –≤—Ā–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ —ā–ĺ—á–ļ–ł—ā–Ķ –ł —Ā–Ľ–Ķ–ī –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ī–ĺ–ļ–į—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —Č–Ķ —Ā–Ķ –ī–ĺ–Ī–Ľ–ł–∂–ł –ľ–į–ļ—Ā–ł–ľ–į–Ľ–Ĺ–ĺ –ī–ĺ –į—ā—Ä–į–ļ—ā–ĺ—Ä–į. –ü–ĺ —ā–į–∑–ł –Ĺ–į—á–ł–Ĺ —Ā—ā–į–≤–į –Ī–Ķ–∑ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ļ–į–ļ–≤–į –Ķ –Ĺ–į—á–į–Ľ–Ĺ–į—ā–į —Ą–ĺ—Ä–ľ–į. –ó–į –ī–į —Ā–Ķ —É–Ī–Ķ–ī–ł—ā–Ķ, —á–Ķ —ā—Ź –ľ–ĺ–∂–Ķ –ī–į –Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į, —Ä–į–∑–≥–Ľ–Ķ–ī–į–Ļ—ā–Ķ –į–Ĺ–ł–ľ–į—Ü–ł–ł—ā–Ķ:
 |
|||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
 |
|||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
–ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ–į–Ņ—Ä–į—ā –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ–Ľ—É—á–ł–ľ –ł –ĺ—ā –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł. –†–Ķ–∑—É–Ľ—ā–į—ā—ä—ā –ĺ—ā –≤—Ā—Ź–ļ–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į –ĺ—ā —á–Ķ—ā–ł—Ä–ł —Ä–Ķ–ī—É–ļ—Ü–ł–ł –ł —á–Ķ—ā–ł—Ä–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –Ĺ–į –Ņ—Ä–Ķ–ī—ą–Ķ—Ā—ā–≤–į—Č–ĺ—ā–嬆–ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ. –ē–ī–Ĺ–ĺ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–ł –ĺ—Ā—ä—Č–Ķ—Ā—ā–≤—Ź–≤–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ —Ä—Ź–∑–ļ–į —Ä–Ķ–ī—É–ļ—Ü–ł—Ź, –≤ —Ä–Ķ–∑—É–Ľ—ā–į—ā –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —Ā–Ķ —Ā–ľ–į—á–ļ–≤–į –≤—ä–≤ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ–į –Ľ–ł–Ĺ–ł—Ź, —ā–į–∑–ł –Ľ–ł–Ĺ–ł—Ź –ĺ–Ī—Ä–į–∑—É–≤–į —Ā—ā—ä–Ī–Ľ–ĺ.
 |
||||
| 1 | 2 | 3 | 4 | 5 |
–í–ł–∂–ī–į—ā–Ķ, —á–Ķ –ī–ĺ—Ä–ł –ī–į –∑–į–Ņ–ĺ—á–≤–į–ľ–Ķ –ĺ—ā –Ķ–ī–Ĺ–į –ł —Ā—ä—Č–į —Ą–ł–≥—É—Ä–į, —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ —Ā–į —Ā—ä–≤—Ā–Ķ–ľ —Ä–į–∑–Ľ–ł—á–Ĺ–ł, –į –į–ļ–ĺ –∑–į–Ņ–ĺ—á–≤–į–ľ–Ķ —Ā —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ą–ł–≥—É—Ä–ł, –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ–Ľ—É—á–ł–ľ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č —Ä–Ķ–∑—É–Ľ—ā–į—ā. –Ę–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –Ņ—ä—Ä–≤–ł—á–Ĺ–į—ā–į —Ą–ł–≥—É—Ä–į –Ķ –Ī–Ķ–∑ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—Č–ł —Ā–į —Ā–į–ľ–ł—ā–Ķ –į—Ą–ł–Ĺ–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł.
¬†–ź–ļ–ĺ –∑–į–Ņ–ĺ—á–Ĺ–Ķ–ľ, –ī–į —Ä–Ķ—á–Ķ–ľ —Ā –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, —Ā–Ľ–Ķ–ī –≤—Ā—Ź–ļ–į —Ā—ā—ä–Ņ–ļ–į (–ł—ā–Ķ—Ä–į—Ü–ł—Ź) –Ī—Ä–ĺ—Ź—ā –Ĺ–į –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł—ā–Ķ —Č–Ķ —Ā–Ķ —É–≤–Ķ–Ľ–ł—á–ł —á–Ķ—ā–ł—Ä–ł –Ņ—ä—ā–ł, –į —Ā–Ľ–Ķ–ī m –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–ł—Ź —Č–Ķ —Ā—ā–į–Ĺ–į—ā 4m –Ī—Ä–ĺ—Ź. –°–Ľ–Ķ–ī —á–Ķ—ā–ł—Ä–ł –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ĺ—ā–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ (–≤ —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ) —ā–ĺ–Ļ –≤—Ā–Ķ –ĺ—Č–Ķ —Ā–Ķ —Ä–į–∑–Ľ–ł—á–į–≤–į. –°–Ľ–Ķ–ī –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, —Ą–ł–≥—É—Ä–į—ā–į –Ĺ–į–ľ–į–Ľ—Ź–≤–į –ł —Ā–Ķ –Ĺ–į—Ā–ĺ—á–≤–į –Ī—ä—Ä–∑–ĺ –ļ—ä–ľ –į—ā—Ä–į–ļ—ā–ĺ—Ä–į. –ó–į –ī–į —Ā—ā–į–Ĺ–Ķ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ—ä—ā –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –ľ–į–Ľ—ä–ļ –ł –ī–į —Ā–Ķ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–į—ā–į —Ą–ĺ—Ä–ľ–į –Ĺ–į –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ (–≤ —Ā–Ľ—É—á–į—Ź –Ņ–į–Ņ—Ä–į—ā), —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤—Ź—ā –Ņ–ĺ–Ĺ–Ķ –ĺ–ļ–ĺ–Ľ–ĺ 50 –ł—ā–Ķ—Ä–į—Ü–ł–ł, –į —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ, –ī–į —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź—ā –ł –Ĺ–į—Ä–ł—Ā—É–≤–į—ā 450 (–ĺ–ļ–ĺ–Ľ–ĺ 1030) –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł. –Ę–ĺ–≤–į —Ā–į —ā–≤—ä—Ä–ī–Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –ł —ā–≤—ä—Ä–ī–Ķ –ľ–Ĺ–ĺ–≥–ĺ –≤—Ä–Ķ–ľ–Ķ –∑–į –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź, –į –∑–į –ī–į —Ā–Ķ —Ā—ā–ł–≥–Ĺ–Ķ –ī–ĺ –į—ā—Ä–į–ļ—ā–ĺ—Ä–į –ł–ľ–į¬†–Ņ–ĺ-–ī–ĺ–Ī—ä—Ä –Ĺ–į—á–ł–Ĺ.
–ė–≥—Ä–į –Ĺ–į —Ö–į–ĺ—Ā
–ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł –Ķ –ł–∑–ĺ–Ī—Ä–Ķ—ā–ł–Ľ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ "–ł–≥—Ä–į –Ĺ–į —Ö–į–ĺ—Ā", –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –≤ —Ā–Ľ–Ķ–ī–Ĺ–ĺ—ā–ĺ:
 |
||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
–Ě–Ķ–ļ–į –Ņ—Ä–ł–Ľ–ĺ–∂–ł–ľ –ľ–Ķ—ā–ĺ–ī–į –≤—ä—Ä—Ö—É —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į –Ĺ–į –°–Ķ—Ä–Ņ–ł–Ĺ—Ā–ļ–ł.¬†–ü–ĺ-–Ņ—Ä–ĺ—Ā—ā–ĺ –Ķ –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā —ā–ĺ—á–ļ–ł.¬†–Ę–į–ļ–į —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź–≤–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–Ľ–Ķ—Ā–Ĺ–ĺ, –∑–į—Č–ĺ—ā–ĺ —Ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–ł—Ä–į —Ā–į–ľ–ĺ –Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į –ĺ—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į. –©–Ķ –∑–į–Ņ–ĺ—á–Ĺ–Ķ–ľ —Ā –Ķ–ī–ł–Ĺ –≤—ä–ĺ–Ī—Ä–į–∂–į–Ķ–ľ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł –ī–į –Ĺ–ĺ–ľ–Ķ—Ä–ł—Ä–į–ľ–Ķ¬†–≤—ä—Ä—Ö–ĺ–≤–Ķ—ā–Ķ –ľ—É —Ā 1, 2, –ł 3. –ė–∑–Ī–ł—Ä–į–ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ĺ –ľ—Ź—Ā—ā–ĺ.¬†–ď–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ł —á–ł—Ā–Ľ–ĺ –ľ–Ķ–∂–ī—É 1 –ł 3. –°–Ľ–Ķ–ī–≤–į—Č–į—ā–į —ā–ĺ—á–ļ–į –Ķ —Ā—Ä–Ķ–ī–į—ā–į –ľ–Ķ–∂–ī—É –Ņ—ä—Ä–≤–į—ā–į —ā–ĺ—á–ļ–į –ł –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –Ĺ–ĺ–ľ–Ķ—Ä –Ĺ–į –≤—ä—Ä—Ö–į¬†–Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į.¬†–ü—Ä–ĺ–ī—ä–Ľ–∂–į–≤–į–ľ–Ķ –ī–į –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–ľ–Ķ —Ā–Ľ—É—á–į–Ļ–Ĺ–ł —á–ł—Ā–Ľ–į –ł –ī–į –ł–∑–ĺ–Ī—Ä–į–∑—Ź–≤–į–ľ–Ķ —Ā—Ä–Ķ–ī–ł—ā–Ķ.¬†–°–Ľ–Ķ–ī –ĺ–ļ–ĺ–Ľ–ĺ —Ö–ł–Ľ—Ź–ī–į –ł—ā–Ķ—Ä–į—Ü–ł–ł, —Č–Ķ –≤–ł–ī–ł–ľ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į –Ĺ–į –°–Ķ—Ä–Ņ–ł–Ĺ—Ā–ļ–ł.
–°–Ķ–≥–į –ī–į –ĺ–Ņ–ł—ā–į–ľ–Ķ —Ā—ä—Č–ł—Ź –ľ–Ķ—ā–ĺ–ī –∑–į –Ľ–ł—Ā—ā–ĺ—ā–ĺ –Ņ–į–Ņ—Ä–į—ā –Ĺ–į –Ď–į—Ä–Ĺ—Ā–Ľ–ł. –ė–≥—Ä–į—ā–į –∑–į–Ņ–ĺ—á–≤–į —Ā –ł–∑–Ī–ĺ—Ä –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į —ā–ĺ—á–ļ–į –ĺ—ā —Ä–į–≤–Ĺ–ł–Ĺ–į—ā–į. –Ę–ĺ–≥–į–≤–į –ł–∑–Ī–ł—Ä–į–ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –ĺ—ā 1 –ī–ĺ 4 –ł–Ľ–ł –≤—Ā–Ķ –Ķ–ī–Ĺ–ĺ, —á–Ķ —Ö–≤—ä—Ä–Ľ—Ź–ľ–Ķ 4-—Ā—ā—Ä–į–Ĺ–Ĺ–ĺ –∑–į—Ä—á–Ķ. –í—Ā—Ź–ļ–į —Ā—ā—Ä–į–Ĺ–į —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į –Ĺ–į –Ķ–ī–Ĺ–į –ĺ—ā —á–Ķ—ā–ł—Ä–ł—ā–Ķ —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, –ļ–ĺ–ł—ā–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –Ľ–ł—Ā—ā–ĺ –Ņ–į–Ņ—Ä–į—ā –ł —ā–į–ļ–į –Ĺ–į —Ā–Ľ—É—á–į–Ķ–Ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –ł–∑–Ī–ł—Ä–į–ľ–Ķ¬†–Ķ–ī–Ĺ–į –ĺ—ā —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł—ā–Ķ
–ź–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ—ä—ā
–ė —ā–į–ļ–į, –ī–į –ĺ–Ņ–ł—ą–Ķ–ľ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ–į –Ĺ–į–ļ—Ä–į—ā–ļ–ĺ:
- –ė–∑–Ī–ł—Ä–į–ľ–Ķ –ĺ–Ī—Č–ł—Ź –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ļ–ĺ–ł—ā–ĺ —Č–Ķ —Ā–Ķ –ł–∑–Ņ—ä–Ľ–Ĺ—Ź–≤–į—ā –ł –≥–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į–ľ–Ķ —Ā¬†m.¬†.
- –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–ľ–Ķ –ĺ–Ī—Č–ł—Ź –Ī—Ä–ĺ–Ļ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –ļ–į—ā–嬆k¬†.
- –ě–Ī–ĺ–∑–Ĺ–į—á–į–≤–į–ľ–Ķ –≤—Ā—Ź–ļ–į —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź —Ā —Ü—Ź–Ľ–ĺ —á–ł—Ā–Ľ–ĺ –ĺ—ā 1 –ī–嬆k¬†.
- –ė–∑–Ī–ł—Ä–į–ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į —ā–ĺ—á–ļ–į –ł —Ź –ĺ–∑–Ĺ–į—á–į–≤–į–ľ–Ķ —Ā a.
- –ď–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–ľ–Ķ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –ĺ—ā 1 –ī–嬆k.
- –Ě–į–ľ–ł—Ä–į–ľ–Ķ —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –Ĺ–ĺ–≤–į—ā–į —ā–ĺ—á–ļ–į a=¬†fk(a) –ļ–į—ā–ĺ —Ä–Ķ–∑—É–Ľ—ā–į—ā –ĺ—ā —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –ł–∑–Ī—Ä–į–Ĺ–į—ā–į —Ą—É–Ĺ–ļ—Ü–ł—Ź –Ņ–ĺ–ī –Ĺ–ĺ–ľ–Ķ—Ä k, fk —Ā –į—Ä–≥—É–ľ–Ķ–Ĺ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–į—ā–į —ā–ĺ—á–ļ–į a –ĺ—ā —Ā—ā—ä–Ņ–ļ–į 4.
- –ü–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–ľ–Ķ¬†a.
- –í—Ä—ä—Č–į–ľ–Ķ —Ā–Ķ –Ĺ–į —Ā—ā—ä–Ņ–ļ–į 5, –Ņ–ĺ–≤—ā–į—Ä—Ź–Ļ–ļ–ł¬†—Ā—ā—ä–Ņ–ļ–ł –ĺ—ā 5 –ī–ĺ 8 m¬†–Ņ—ä—ā–ł.
–ü—Ä–ł–Ľ–į–≥–į–Ļ–ļ–ł —ā–ĺ–∑–ł –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –Ĺ–į –Ņ–į–Ņ—Ä–į—ā—ā–į –Ĺ–į –Ď–į—Ä–Ĺ—Ā–Ľ–ł, –Ņ–ĺ–Ľ—É—á–į–≤–į–ľ–Ķ:
 |
|||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
–ö–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł—ā–Ķ –Ĺ–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā
–í —ā–ĺ–∑–ł –Ņ—Ä–ł–ľ–Ķ—Ä –≤—Ā—Ź–ļ–į
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ł –Ľ–Ķ–ļ—Ā–ł–ļ–į
- –ź—Ą–ł–Ĺ–Ĺ–ł (–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł) —ā—Ä–į–Ĺ—Ā—Ą–ĺ—Ä–ľ–į—Ü–ł–ł
- –°–ł—Ā—ā–Ķ–ľ–ł –ė—ā–Ķ—Ä–į—ā–ł–≤–Ĺ–ł –§—É–Ĺ–ļ—Ü–ł–ł (Iterated Functions System - IFS)
- –ź—ā—Ä–į–ļ—ā–ĺ—Ä–ł
- –ė–≥—Ä–į –Ĺ–į —Ö–į–ĺ—Ā
- –ö–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ł –Ĺ–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā
- –§—Ä–į–ļ—ā–į–Ľ–ł
- –Ē—Ä–į–ļ–ĺ–Ĺ –Ĺ–į –•–į—Ä—ā–Ķ—Ä-–•–Ķ–Ļ—ā—É–Ķ–Ľ
- –ö—Ä–ł–≤–į –Ĺ–į –ö–ĺ—Ö
- –ü–į–Ņ—Ä–į—ā –Ĺ–į –Ď–į—Ä–Ĺ—Ā–Ľ–ł
- –Ē–∂–ĺ–Ĺ –•—ä—ā—á–ł–Ĺ—Ā—ä–Ĺ
- –ú–į–Ļ–ļ—ä–Ľ –Ď–į—Ä–Ĺ—Ā–Ľ–ł
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
–§—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–į—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ņ—Ä–ł—Ä–ĺ–ī—č, –ú–į–Ĺ–ī–Ķ–Ľ—Ć–Ī—Ä–ĺ—ā –Ď.
Fractal Geometry, Yale University, Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger
–í–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –≤–ĺ —Ą—Ä–į–ļ—ā–į–Ľ—č, –®–į–Ī–į—Ä—ą–ł–Ĺ –ź.–ź.
Fractals: Useful Beauty (General Introduction to Fractal Geometry)
–Į–∑—č–ļ —Ą—Ä–į–ļ—ā–į–Ľ–ĺ–≤, –•–ź–†–Ę–ú–£–Ę –ģ–†–ď–ē–Ě–°, –•–ź–ô–Ě–¶-–ě–Ę–Ę–ě –ü–ź–ô–Ę–ď–ē–Ě, –Ē–ė–Ę–ú–ź–† –ó–ź–£–ü–ē
–ě—Ā–Ĺ–ĺ–≤—č —Ą—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā–∂–į—ā–ł—Ź –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ



















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Nikor
–Ě–į 30 —Ā–Ķ–Ņ—ā–Ķ–ľ–≤—Ä–ł 1928 –Ķ –ĺ—ā–ļ—Ä–ł—ā –Ņ–Ķ–Ĺ–ł—Ü–ł–Ľ–ł–Ĺ—ä—ā
–ü—Ä–ĺ—Ā—ā –ß–ĺ–≤–Ķ–ļ
–Ě–ĺ–≤–ĺ –ĺ–Ī—Ź—Ā–Ĺ–Ķ–Ĺ–ł–Ķ –∑–į –≥–ł–≥–į–Ĺ—ā—Ā–ļ–ł—ā–Ķ –Ķ–ļ—Ā–Ņ–Ľ–ĺ–ī–ł—Ä–į—Č–ł –ļ—Ä–į—ā–Ķ—Ä–ł –≤ –°–ł–Ī–ł—Ä
dolivo
–ö–Ľ–ł–ľ–į—ā–ł—á–Ĺ–ł—Ź—ā —Ā–ļ–Ķ–Ņ—ā–ł—Ü–ł–∑—ä–ľ ‚Äď –Ĺ–į–Ļ-—Ā–ļ—ä–Ņ–į—ā–į –Ľ—ä–∂–į –Ĺ–į –Ĺ–į—ą–Ķ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ
helper68
–ė–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā–ľ–į—Ä—ā—Ą–ĺ–Ĺ –≤ —ā–ĺ–į–Ľ–Ķ—ā–Ĺ–į—ā–į –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–ĺ —Ā 46% –Ņ–ĺ-–≤–ł—Ā–ĺ–ļ —Ä–ł—Ā–ļ –ĺ—ā —Ö–Ķ–ľ–ĺ—Ä–ĺ–ł–ī–ł