

–í—ä–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ
–ó–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ¬†–Ķ –Ķ–ī–Ĺ–į –ĺ—ā –Ĺ–į–Ļ-—Ź—Ä–ļ–ł—ā–Ķ –ł —É—Ā—ā–ĺ–Ļ—á–ł–≤–ł –Ņ—Ä–ĺ—Ź–≤–ł –Ĺ–į —Ö–į—Ä–ľ–ĺ–Ĺ–ł—Ź –Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į. –Ē–ĺ–ļ–į—ā–ĺ –§—ä–Ĺ –®—É–Ļ –Ķ –ł–∑—ā–ĺ—á–Ĺ–ł—Ź—ā –Ņ–ĺ–ī—Ö–ĺ–ī –ļ—ä–ľ —Ö–į—Ä–ľ–ĺ–Ĺ–ł—Ź –ł –Ī–į–Ľ–į–Ĺ—Ā, –Ĺ–į –ó–į–Ņ–į–ī —Ā–Ķ –Ņ—Ä–ł–Ľ–į–≥–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ł —á–ł—Ā–Ľ–ĺ–≤ –Ņ–ĺ–ī—Ö–ĺ–ī –∑–į –ł–∑–ľ–Ķ—Ä–≤–į–Ĺ–Ķ –∑–į —Ā—ä—Č–ĺ—ā–ĺ - –∑–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ.¬†
–ß–ĺ–≤–Ķ–ļ —Ö–į—Ä–Ķ—Ā–≤–į –Ĺ—Ź–ļ–į–ļ—ä–≤ –Ņ—Ä–Ķ–ī–ľ–Ķ—ā –∑–į—Ä–į–ī–ł —Ą–ĺ—Ä–ľ–į—ā–į –ľ—É. –£—Ā–Ķ—Č–į–Ĺ–Ķ—ā–ĺ –∑–į –ļ—Ä–į—Ā–ĺ—ā–į –ł —Ö–į—Ä–ľ–ĺ–Ĺ–ł—Ź –Ĺ–į–Ļ-—á–Ķ—Ā—ā–ĺ –Ņ—Ä–ĺ–ł–∑—ā–ł—á–į –ĺ—ā —Ā—ä—á–Ķ—ā–į–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ā–ł–ľ–Ķ—ā—Ä–ł—Ź –ł –∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ. –¶—Ź–Ľ–ĺ—ā–ĺ –≤–ł–Ĺ–į–≥–ł —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā —á–į—Ā—ā–ł –ł –į–ļ–ĺ —ā–Ķ —Ā–į –≤ "–∑–Ľ–į—ā–Ĺ–ĺ" —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ - –Ņ–ĺ–ľ–Ķ–∂–ī—É —Ā–ł –ł —Ā —Ü—Ź–Ľ–ĺ—ā–ĺ, —ā–ĺ —ā–ĺ–≤–į –≤–ł–Ĺ–į–≥–ł –Ķ –Ī–Ķ–Ľ–Ķ–≥ –Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–Ĺ–ĺ –ł —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ĺ —Ā—ä–≤—ä—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ –≤ –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ, –Ĺ–į—É–ļ–į—ā–į, —ā–Ķ—Ö–Ĺ–ł–ļ–į—ā–į –ł –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į.
| –ě—Č–Ķ –Ņ—Ä–Ķ–∑ –†–Ķ–Ĺ–Ķ—Ā–į–Ĺ—Ā–į —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł—ā–Ķ –ĺ—ā–ļ—Ä–ł–Ľ–ł, —á–Ķ –≤—Ā—Ź–ļ–į –ļ–į—Ä—ā–ł–Ĺ–į –ł–ľ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–ł–ļ–ĺ–≤–į–≤–į—ā –Ĺ–į—ą–Ķ—ā–ĺ –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, —ā. –Ĺ. –∑—Ä–ł—ā–Ķ–Ľ–Ĺ–ł —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤–Ķ. –Ę–Ķ —Ā–į 4 –ł —Ā–į —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ 3/8 –ł 5/8 –ĺ—ā –ļ—Ä–į–ł—Č–į—ā–į –Ĺ–į –Ņ–Ľ–į—ā–Ĺ–ĺ—ā–ĺ. –Ę–ĺ–≤–į –ĺ—ā–ļ—Ä–ł—ā–ł–Ķ —ā–Ķ –Ĺ–į—Ä–Ķ–ļ–Ľ–ł "–∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ" –Ĺ–į –ļ–į—Ä—ā–ł–Ĺ–į—ā–į. –ź–ļ–ĺ –ł—Ā–ļ–į–ľ–Ķ –ī–į –į–ļ—Ü–Ķ–Ĺ—ā–ł—Ä–į–ľ–Ķ –Ĺ–į –Ĺ—Ź–ļ–ĺ–Ļ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā –ĺ—ā –ļ–į—Ä—ā–ł–Ĺ–į—ā–į (—Ą–ĺ—ā–ĺ–≥—Ä–į—Ą–ł—Ź—ā–į) —ā—Ä—Ź–Ī–≤–į –ī–į –≥–ĺ —Ā–Ľ–ĺ–∂–ł–ľ –≤ –Ķ–ī–ł–Ĺ –ĺ—ā –∑—Ä–ł—ā–Ķ–Ľ–Ĺ–ł—ā–Ķ —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤–Ķ. |  |
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ
 |
|
–Ę–ĺ–≤–į —á–ł—Ā–Ľ–ĺ —Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į —Ā–Ķ —Ā –≥–Ľ–į–≤–Ĺ–į—ā–į –≥—Ä—ä—Ü–ļ–į –Ī—É–ļ–≤–į –§ (—Ą–ł) - –Ņ—ä—Ä–≤–į—ā–į –Ī—É–ļ–≤–į –≤ –ł–ľ–Ķ—ā–ĺ –Ĺ–į –§–ł–ī–ł–Ļ.
–õ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–ĺ –Ķ, —á–Ķ 1/–§ = 0.61803398... –ß–ł—Ā–Ľ–ĺ—ā–ĺ –§ –Ķ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ—ā–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ, –ļ–ĺ–Ķ—ā–ĺ —Ā–Ķ –Ņ—Ä–Ķ–≤—Ä—ä—Č–į –≤ —Ä–Ķ—Ü–ł–Ņ—Ä–ĺ—á–Ĺ–ĺ—ā–ĺ —Ā–ł –Ņ—Ä–ł –ł–∑–≤–į–∂–ī–į–Ĺ–Ķ –Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į. –ú–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ł –ļ–į—ā–ĺ —Ā—É–ľ–į –ĺ—ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł—Ź —Ä–Ķ–ī: –§=1+1/(1+1/(1+1/(1+ ...
–ł–Ľ–ł –§=‚ąö(1+‚ąö(1+‚ąö(1+‚ąö(1+‚ąö(1+‚ąö(1+...))))))
–§ –Ķ –≥—Ä–į–Ĺ–ł—Ü–į—ā–į, –ļ—ä–ľ –ļ–ĺ—Ź—ā–ĺ —Ā–Ķ —Ā—ā—Ä–Ķ–ľ–ł –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ī–≤–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł —á–Ľ–Ķ–Ĺ–į –ĺ—ā —Ä–Ķ–ī–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł.¬†
–ó–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ: 1,61803398874989484820 ... (–ł —ā.–Ĺ.) –Ĺ—Ź–ľ–į –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ —ā–ĺ—á–Ĺ–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā, —ā–ĺ –Ķ –ł—Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ.
–í –ö–Ĺ–ł–≥–į 6, –Ĺ–į "–Ě–į—á–į–Ľ–į" –ē–≤–ļ–Ľ–ł–ī –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į –∑–į–ī–į—á–į—ā–į –∑–į "–ī–Ķ–Ľ–Ķ–Ĺ–Ķ –Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į –≤ –ļ—Ä–į–Ļ–Ĺ–ĺ –ł —Ā—Ä–Ķ–ī–Ĺ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ", –į —ā–Ķ—Ä–ľ–ł–Ĺ—ä—ā "–∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ" –≤—ä–≤–Ķ–∂–ī–į –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł, –ļ–ĺ–Ļ—ā–ĺ –≥–ĺ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ľ –ļ–į—ā–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź –Ĺ–į "–ł–ī–Ķ–į–Ľ–Ĺ–ĺ—ā–ĺ —á–ĺ–≤–Ķ—ą–ļ–ĺ —ā—Ź–Ľ–ĺ". –ü–ĺ-–ļ—ä—Ā–Ĺ–ĺ –Ĺ–į—Ä–ł—á–į—ā –∑–Ľ–į—ā–Ĺ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź, –∑–Ľ–į—ā–Ķ–Ĺ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ł –ī–į–∂–Ķ –Ī–ĺ–∂–Ķ—Ā—ā–≤–Ķ–Ĺ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź. –í–Ķ–Ľ–ł–ļ–ł—Ź—ā –į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ –ĺ—ā XVI-—ā–ł –≤–Ķ–ļ –ô–ĺ—Ö–į–Ĺ –ö–Ķ–Ņ–Ľ–Ķ—Ä –Ĺ–į—Ä–ł—á–į –∑–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ "–Ķ–ī–Ĺ–ĺ –ĺ—ā —Ā—ä–ļ—Ä–ĺ–≤–ł—Č–į—ā–į –Ĺ–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į".
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź
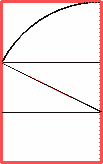
–ě—ā "–Ě–į—á–į–Ľ–į" –Ĺ–į –ē–≤–ļ–Ľ–ł–ī –Ķ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ —Ā–Ľ–Ķ–ī–Ĺ–ł—Ź –Ĺ–į—á–ł–Ĺ –∑–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į "–∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ" —Ā –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ľ–ł–Ĺ–ł–Ļ–ļ–į –ł –Ņ–Ķ—Ä–≥–Ķ–Ľ.
–ě—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ–Ĺ–į—ā–į (Orthogons) —Ā–ł—Ā—ā–Ķ–ľ–į –∑–į –ī–ł–∑–į–Ļ–Ĺ –ĺ—ā –≤–Ķ–ļ–ĺ–≤–Ķ –Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į–Ľ–į –Ĺ–į —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł –ł –∑–į–Ĺ–į—Ź—ā—á–ł–ł –ī–į —Ā—ä–∑–ī–į–≤–į—ā —Ö–į—Ä–ľ–ĺ–Ĺ–ł—á–Ĺ–ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ī–Ķ–∑ —Ā–Ľ–ĺ–∂–Ĺ–ł –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź.
 |
 |
 |
 |
| Auron (–ó–Ľ–į—ā–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ) 1/2 + ‚ąö5/2 =1.618... = ő¶ | Diagon ‚ąö2 =1.414... –§–ĺ—Ä–ľ–į—ā–ł –ź4, –ź3 –ł —ā.–Ĺ. | Quadriagon 1/2 + ‚ąö2/2 =1.207... | –ü–ĺ–Ľ—É diagon ‚ąö5/2 =1.118... |
 
–ó–Ľ–į—ā–Ĺ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł —Ą–ł–≥—É—Ä–ł
–ó–Ľ–į—ā–Ĺ–ł –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł —Ā–į –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł, —á–ł–ł—ā–ĺ —Ā—ā—Ä–į–Ĺ–ł —Ā–į –≤ "–∑–Ľ–į—ā–Ĺ–ĺ" —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ. "–ó–Ľ–į—ā–Ĺ–ł—Ź—ā" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł–ľ–į –Ĺ—Ź–ļ–ĺ–ł –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į.
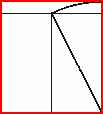
| –ź–ļ–ĺ –ĺ—ā—Ä–Ķ–∂–Ķ–ľ –ĺ—ā "–∑–Ľ–į—ā–Ĺ–ł—Ź" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –ļ–≤–į–ī—Ä–į—ā, —Ā—ā—Ä–į–Ĺ–į—ā–į –Ĺ–į –ļ–ĺ–Ļ—ā–ĺ –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į –Ņ–ĺ-–ľ–į–Ľ–ļ–į—ā–į —Ā—ā—Ä–į–Ĺ–į –Ĺ–į –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ–į, –ĺ—Ā—ā–į—ā—ä–ļ–į —Č–Ķ –Ī—ä–ī–Ķ –ĺ—ā–Ĺ–ĺ–≤–ĺ "–∑–Ľ–į—ā–Ķ–Ĺ" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, –Ĺ–ĺ —Ā –Ņ–ĺ-–ľ–į–Ľ–ļ–ł —Ä–į–∑–ľ–Ķ—Ä–ł.
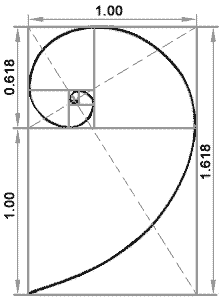
–ź–ļ–ĺ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–ł–ľ –ī–į –ĺ—ā—Ä—Ź–∑–≤–į–ľ–Ķ –ļ–≤–į–ī—Ä–į—ā–ł, —Č–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į–ľ–Ķ –≤—Ā–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ł –ł –Ņ–ĺ-–ľ–į–Ľ–ļ–ł "–∑–Ľ–į—ā–Ĺ–ł" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł. –ü—Ä–ł —ā–ĺ–≤–į —Č–Ķ —Ā–į –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ł –Ņ–ĺ –Ľ–ĺ–≥–į—Ä–ł—ā–ľ–ł—á–Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į, —Ā—ä–≤—Ā–Ķ–ľ —Ā—ä—Č–į—ā–į –ļ–į—ā–ĺ —ā–į–∑–ł, –ļ–ĺ—Ź—ā–ĺ —Ā–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į –ĺ—ā –ļ–≤–į–ī—Ä–į—ā–ł —Ā—ä—Ā —Ā—ā—Ä–į–Ĺ–ł, —á–ł—Ā–Ľ–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł. –ü–ĺ–Ľ—é—Ā—ä—ā –Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į—ā–į –Ľ–Ķ–∂–ł –Ĺ–į –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł—ā–Ķ –Ĺ–į –Ĺ–į—á–į–Ľ–Ĺ–ł—Ź –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł –Ņ—ä—Ä–≤–ł—Ź –ĺ—ā—Ä—Ź–∑–į–Ĺ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ. –ü—Ä–ł —ā–ĺ–≤–į –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł—ā–Ķ –Ĺ–į –≤—Ā–ł—á–ļ–ł —Ā–Ľ–Ķ–ī–≤–į—Č–ł –Ĺ–į–ľ–į–Ľ—Ź–≤–į—Č–ł "–∑–Ľ–į—ā–Ĺ–ł" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –Ľ–Ķ–∂–į—ā –Ĺ–į —ā–Ķ–∑–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł. ¬† |
 |
 |
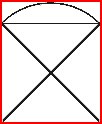
–ź–ļ–ĺ —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–ł–ľ —ā—Ä–ł "–∑–Ľ–į—ā–Ĺ–ł" –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł —ā–į–ļ–į, —á–Ķ –≤—Ā–Ķ–ļ–ł —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į —Ā –ī–≤–į –ī—Ä—É–≥–ł (–Ņ–ĺ–ī –Ņ—Ä–į–≤ —ä–≥—ä–Ľ –≤—Ā–Ķ–ļ–ł –ļ—ä–ľ –≤—Ā–Ķ–ļ–ł, —Č–Ķ –≤–ł–ī–ł–ľ —á–Ķ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į—ā–į –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł—Ź –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –≤–Ņ–ł—ą–Ķ –≤: |
|
|
|
 
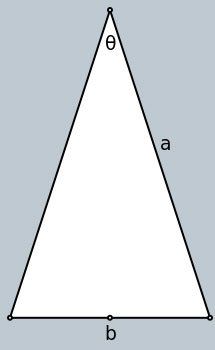 –ó–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ
–ó–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ
–ó–Ľ–į—ā–Ĺ–ł—Ź—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ķ –Ĺ–į—Ä–ł—á–į–Ĺ –ĺ—Č–Ķ "—Ā—ä–≤—ä—Ä—ą–Ķ–Ŭ†—ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ". –Ę–ĺ–Ļ –Ķ¬†—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ī–Ķ–ī—Ä–į—ā–į —Ā–į –≤ –∑–Ľ–į—ā–Ĺ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź —Ā –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į:
![]()
–ó–Ľ–į—ā–Ĺ–ł—Ź —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –Ķ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –ł –Ņ—Ä–ł —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ 2:2:1 –Ĺ–į –≤—ä—ā—Ä–Ķ—ą–Ĺ–ł—ā–Ķ —ä–≥–Ľ–ł –Ĺ–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł–Ľ–ł 72¬į.: 72¬į:¬†36¬į.
–ü–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ
–ė–ľ–į –ľ–Ĺ–ĺ–≥–ĺ –Ĺ–į—á–ł–Ĺ–ł –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –∑–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ĺ—ā —ā—Ź—Ö –Ņ—Ä–Ķ–ľ–ł–Ĺ–į–≤–į—ā –Ņ—Ä–Ķ–∑ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–į–≤–ł–Ľ–Ķ–Ĺ –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, –Ĺ–ĺ —Ā–į –Ņ–ĺ-—Ā–Ľ–ĺ–∂–Ĺ–ł, –∑–į—Č–ĺ—ā–ĺ –ł–∑–ł—Ā–ļ–≤–į—ā –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł —Ā–į–ľ–ł—Ź –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ.

–Ě–į–Ļ-–Ņ—Ä–Ķ–ļ–ł—Ź—ā –ł –Ņ—Ä–ĺ—Ā—ā –Ĺ–į—á–ł–Ĺ –ł–ľ–į –∑–į –ĺ—Ā–Ĺ–ĺ–≤–į –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł—ā–Ķ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –≤ –∑–Ľ–į—ā–Ĺ–ł—Ź –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ. –ó–į –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā–Ķ –∑–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ĺ–į –ī–į–ī–Ķ–Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į AB, —ā—Ä—Ź–Ī–≤–į¬†–ī–į –Ĺ–į–Ņ—Ä–į–≤–ł—ā–Ķ —Ā–Ľ–Ķ–ī–Ĺ–ĺ—ā–ĺ:
- –Ě–į—á–Ķ—Ä—ā–į–Ļ—ā–Ķ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–ł –Ľ–ł–Ĺ–ł–ł —Ā–Ņ—Ä–į–ľ–ĺ –ī–≤–į—ā–į –ļ—Ä–į—Ź –Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į—ā–į AB;
- –Ě–į—á–Ķ—Ä—ā–į–Ļ—ā–Ķ –ī—ä–≥–į —Ā —Ü–Ķ–Ĺ—ā—ä—Ä –Ķ–ī–Ĺ–į—ā–į –ĺ—ā –ī–≤–Ķ—ā–Ķ –ļ—Ä–į–Ļ–Ĺ–ł —ā–ĺ—á–ļ–ł, –≤ —Ā–Ľ—É—á–į—Ź –° —Ā —Ä–į–ī–ł—É—Ā, —Ä–į–≤–Ķ–Ĺ –Ĺ–į –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–į—ā–į –ĺ—ā AB;
- –° —Ü–Ķ–Ĺ—ā—ä—Ä –≤ C –ł —Ä–į–ī–ł—É—Ā –ī—Ä—É–≥–ł—Ź –ļ—Ä–į–Ļ –Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į—ā–į CB, –∑–į—Ā–ł—á–į—ā–Ķ –Ņ—Ä–į–≤–į—ā–į, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ļ–ļ–ł —ā–ĺ—á–ļ–į D;
- –° —Ü–Ķ–Ĺ—ā—ä—Ä A –ł —Ä–į–ī–ł—É—Ā –Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–į—ā–į –ī—ä–Ľ–∂–ł–Ĺ–į AD, –∑–į—Ā–ł—á–į—ā–Ķ —Ā –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–į –ĺ—ā —Ā—Ä–Ķ–ī–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į—ā–į –ł–Ľ–ł —Ā –ī—ä–≥–į —Ā—ä—Ā —Ā—ä—Č–ł—Ź —Ä–į–ī–ł—É—Ā —Ā –ī—ä–Ľ–∂–ł–Ĺ–į AD¬†–ł —Ü–Ķ–Ĺ—ā—ä—Ä B. –Ę–į–ļ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–ľ–Ķ —ā—Ä–Ķ—ā–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –∑–Ľ–į—ā–Ĺ–ł—Ź —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ.

–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ—Ā—ā–ł¬†
–ó–Ľ–į—ā–Ĺ–ł—Ź—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ł–ľ–į –ľ–Ĺ–ĺ–≥–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į, –ĺ–Ī—Č–ł —Ā —ā–Ķ–∑–ł –Ĺ–į –∑–Ľ–į—ā–Ĺ–ł—Ź –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ. –ě—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ—ā–ĺ —Ā–ł –∑–į —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į —ä–≥–Ľ–ł—ā–Ķ 2:2:1, —Ā–Ľ–Ķ–ī–≤–į, —á–Ķ —ä–≥—ä–Ľ–ł—ā–Ķ –≤ –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į —Ā–į –Ņ–嬆72 ¬į –ł —Ā–į –ī–≤–ĺ–Ļ–Ĺ–ĺ –Ņ–ĺ-–≥–ĺ–Ľ–Ķ–ľ–ł –ĺ—ā —ä–≥—ä–Ľ—ä—ā –Ĺ–į –≤—ä—Ä—Ö–į. –Ę–ĺ–≥–į–≤–į –ľ–ĺ–∂–Ķ—ā–Ķ –ī–į —Ä–į–∑–ī–Ķ–Ľ—Ź—ā–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –Ķ–ī–ł–Ĺ–ł—Ź –ĺ—ā —ā—Ź—Ö –ł —Č–Ķ –Ņ–ĺ–Ľ—É—á–ł—ā–Ķ ¬†–Ķ–ī–Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–į –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į –ĺ—ā –∑–Ľ–į—ā–Ĺ–ł –≤—Ā–Ķ –Ņ–ĺ-–ľ–į–Ľ–ļ–ł —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł. –°–≤—ä—Ä–∑–≤–į–Ļ–ļ–ł —Ā –ī—ä–≥–ł —Ā —Ü–Ķ–Ĺ—ā—ä—Ä –≤—ä—Ä—Ö–į –Ĺ–į –ī–ĺ–Ņ—ä–Ľ–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ł—Ź —ā—ä–Ņ–ĺ—ä–≥—ä–Ľ–Ķ–Ĺ —Ā—ä—Č–ĺ "–∑–Ľ–į—ā–Ķ–Ĺ" —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ, —Ä–į–ī–ł—É—Ā –Ī–Ķ–ī—Ä–į—ā–į –ľ—É –ł –ī—ä–Ľ–∂–ł–Ĺ–į —ā—ä–Ņ–ł—Ź —ä–≥—ä–Ľ 108¬į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–į—ā–Ķ–Ľ–Ĺ–ĺ, —Č–Ķ –Ņ–ĺ–Ľ—É—á–ł–ľ —Ā—ä—Č–į—ā–į —Ā–Ņ–ł—Ä–į–Ľ–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł¬†–ł–Ľ–ł "–ó–Ľ–į—ā–Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į", –ļ–ĺ–Ķ—ā–ĺ —Ā–ł –Ķ –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ.
–Ę–į–∑–ł —Ā–Ņ–ł—Ä–į–Ľ–į —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ł –Ľ–ĺ–≥–į—Ä–ł—ā–ľ–ł—á–Ĺ–į,¬†–ļ–į—ā–ĺ –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā¬†—Ā–Ķ —Ā–Ņ–ĺ–ľ–Ķ–Ĺ–į–≤–į –ĺ—ā –†–Ķ–Ĺ–Ķ –Ē–Ķ–ļ–į—Ä—ā.¬† –Ď–Ķ—Ä–Ĺ—É–Ľ–ł (1692), –ļ–ĺ–Ļ—ā–ĺ —Ź –Ĺ–į–∑–ĺ–≤–į–≤–į "—á—É–ī–Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į" ("spira mirabilis").¬†
–ė–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ĺ—ā–ĺ –Ĺ–į —ā–į–∑–ł –ļ—Ä–į—Ā–ł–≤–į –ļ—Ä–ł–≤–į –Ķ, —á–Ķ –≤—ä–≤ –≤—Ā—Ź–ļ–į –Ĺ–Ķ–Ļ–Ĺ–į —ā–ĺ—á–ļ–į –≤–Ķ–ļ—ā–ĺ—Ä—ä—ā, –ļ–ĺ–Ļ—ā–ĺ —Ź —Ā–≤—ä—Ä–∑–≤–į —Ā —Ü–Ķ–Ĺ—ā—ä—Ä–į, —Ā–ļ–Ľ—é—á–≤–į —Ā –ī–ĺ–Ņ–ł—Ä–į—ā–Ķ–Ľ–Ĺ–į—ā–į –≤ —ā–į–∑–ł —ā–ĺ—á–ļ–į –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ķ–Ĺ —ä–≥—ä–Ľ. –Ę—Ź –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–ł—á–Ĺ–ĺ —Ā–Ķ —Ā—ā—Ä–Ķ–ľ–ł –ļ—ä–ľ —Ü–Ķ–Ĺ—ā—ä—Ä–į –ł –Ĺ—Ź–ľ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –∑–į–≤–ĺ–ł - —ā–Ķ —Ā–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł –ł —ā—Ź –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č –Ĺ–į—á–ł–Ĺ, –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –ľ–į—Č–į–Ī–į.
–ó–Ľ–į—ā–Ĺ–ł—Ź—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ—ā–ļ—Ä–ł–Ķ –≤ –ī—Ä—É–≥–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł —Ą–ł–≥—É—Ä–ł:
–Ē–Ķ—Ā–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ |
–ü–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ |
–ü–Ķ–Ĺ—ā–į–≥—Ä–į–ľ |
–ó–Ľ–į—ā–Ĺ–į—ā–į –Ņ–Ķ—ā–ĺ–Ľ—ä—á–ļ–į

–ė–∑–≤–Ķ—Ā—ā–Ĺ–į—ā–į –Ĺ–ł –Ņ–Ķ—ā–ĺ–Ľ—ä—á–ļ–į (–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ-–ĺ—ā –≥—Ä. "pentagrammon", "pente" - –Ņ–Ķ—ā –ł "gramma" - –Ľ–ł–Ĺ–ł–ł) –Ķ –ī—Ä–Ķ–≤–Ķ–Ĺ —Ā–ł–ľ–≤–ĺ–Ľ, –ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ –ĺ—ā 5 "–∑–Ľ–į—ā–Ĺ–ł" —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł, –≤–Ņ–ł—Ā–į–Ĺ–ł –≤ –Ņ—Ä–į–≤–ł–Ľ–Ķ–Ĺ –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –í—Ā—Ź–ļ–į –ĺ—ā –Ņ–Ķ—ā—ā–Ķ –Ľ–ł–Ĺ–ł–ł, —Ā—ä—Ā—ā–į–≤—Ź—Č–ł —ā–į–∑–ł —Ą–ł–≥—É—Ä–į, –ī–Ķ–Ľ–ł –ī—Ä—É–≥–į—ā–į –≤ "–∑–Ľ–į—ā–Ĺ–į" –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź.
 –°—Ö–Ķ–ľ–į—ā–į –≤–Ľ—Ź–≤–ĺ –Ņ–ĺ–ļ–į–∑–≤–į –ļ–į–ļ –ľ–ĺ–∂–Ķ –ļ–≤–į–ī—Ä–į—ā –ł –ī–≤–į –∑–Ľ–į—ā–Ĺ–ł –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź—ā¬†–ļ—ä–ľ¬†–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–į.
–°—Ö–Ķ–ľ–į—ā–į –≤–Ľ—Ź–≤–ĺ –Ņ–ĺ–ļ–į–∑–≤–į –ļ–į–ļ –ľ–ĺ–∂–Ķ –ļ–≤–į–ī—Ä–į—ā –ł –ī–≤–į –∑–Ľ–į—ā–Ĺ–ł –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ—Ź—ā¬†–ļ—ä–ľ¬†–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–į.
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ł –Ľ–Ķ–ļ—Ā–ł–ļ–į
- –ó–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ, —Ā—ä–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ, –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź, –∑–Ľ–į—ā–Ķ–Ĺ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā, –Ī–ĺ–∂–Ķ—Ā—ā–≤–Ķ–Ĺ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź, Auron
- –†–Ķ–ī –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł
- Diagon
- Quadriagon
- –ė—Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ
- –ó–Ľ–į—ā–Ĺ–ł –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł
- –ł–ļ–ĺ—Ā–į–Ķ–ī—ä—Ä
- –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—ä—Ä
- –ó–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ
- –ó–Ľ–į—ā–Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į, –Ľ–ĺ–≥–į—Ä–ł—ā–ľ–ł—á–Ĺ–į —Ā–Ņ–ł—Ä–į–Ľ–į,¬†spira mirabilis
- –ó–Ľ–į—ā–Ĺ–į –Ņ–Ķ—ā–ĺ–Ľ—ä—á–ļ–į
- –§–ł–ī–ł–Ļ
- –ē–≤–ļ–Ľ–ł–ī
- –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł
- –ô–ĺ—Ö–į–Ĺ –ö–Ķ–Ņ–Ľ–Ķ—Ä
- –§–ł–Ī–ĺ–Ĺ–į—á–ł
- –†–Ķ–Ĺ–Ķ –Ē–Ķ–ļ–į—Ä—ā
- –Ď–Ķ—Ä–Ĺ—É–Ľ–ł
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
–ó–ĺ–Ľ–ĺ—ā–ĺ–Ķ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ –ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź
Phi: That Golden Number, Mark Freitag
Fibonacci Number, Mathworld Wolfram


 –ó–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ
–ó–Ľ–į—ā–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ



















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.