Таблицата за умножение на положителни цели числа, учена с толкова досада от малките ученици, крие неочаквани симетрии, открити от един френски учител в начално училище Зуйер Барка, представен в Plus magazine.
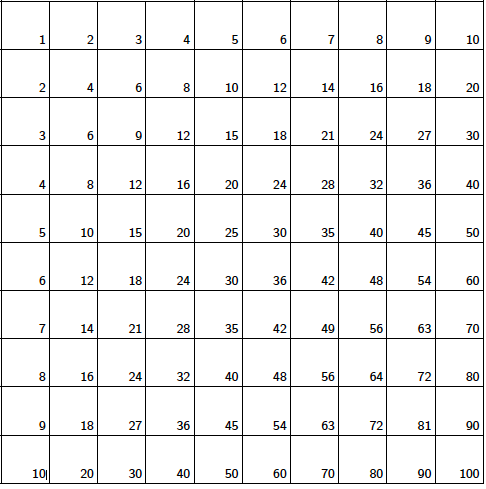
Да започнем със стандартната таблица за умножение. Таблицата по-долу съдържа числата от 1 до 10 в първия ред и първата колона. Всяко друго квадратче съдържа произведението от числото в първия ред и числото в първата колона.
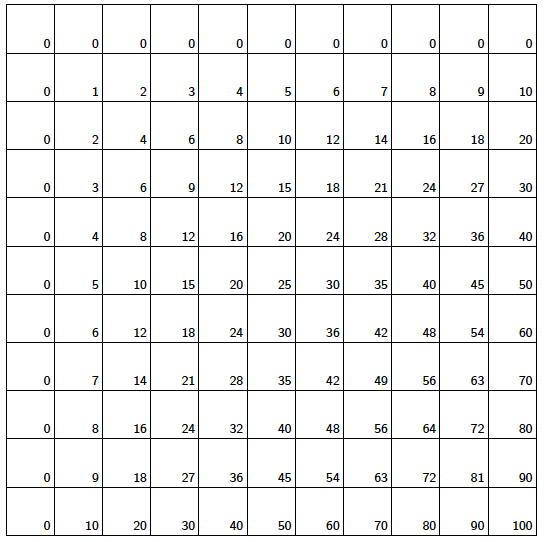
Ние ще добавим един ред 0 в горната част и колона 0 отляво. Това ще осигури повече логичност на таблицата - първият ред и колона съдържат числа, кратни на 0, вторият ред и колона съдържат кратни на 1, третият ред и колона съдържат кратни на 2, и т.н. - и ще осигури хубава рамка за моделите.
По-нататък ще оцветим квадратчетата на таблицата за умножение, които отговарят на кратни на k различни стойности. И ще откриете някои красиви симетрии.
Единични кратните
Ще започнем с k = 2. Присвояваме син цвят за всеки квадратче в таблицата за умножение, което се дели на 2. (Числото 0 е кратно на 2, така че всички нулеви квадратчета са сини.)
Тук предоставяме таблицата малко по-голяма, до числото 15 в хоризонтална посока. Всъщност, тъй като таблицата за умножение на положителни числа е безкрайна и в двете посоки, ние ще я продължаваме, за да се покажат нововъзникващите модели по-ясно.
Целият модел по-горе може да бъде сглобен с помощта на един основен градивен елемент:
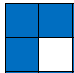
Основният изграждащ блок съдържа k x k = 2 x 2 = 4 клетки на таблицата за умножение. Квадратчетата обозначени с бели клетки в модела се състоят от
(k - 1)2 = (2 - 1)2 = 1
клетки.
По-долу са още две изображения, в които кратни на са оцветени в синьо. Можете ли да кажете, която е стойността на k във всеки един случай? Можете ли да кажете какви са основните градивни елементи, колко клетки съдържат и колко клетки са определени като бели?
Множество кратни на последователни числа
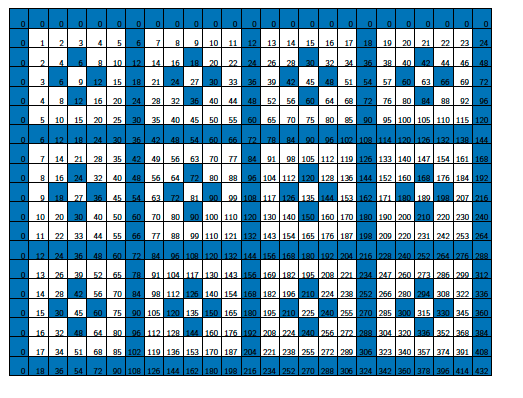
По-интересно се откроява модела, ако се използват няколко кратни и съответстващи на тях, повече цветове. На следващата фигура числата, които са кратни на 2 са оцветени в червено, а тези, които са кратни на 3, са оцветени в оранжево (с оранжево са и тези, които са кратни и на 2, и на 3, тоест, кратни на 6).
Това дава следния модел.
Имайте предвид, че този път нашите основни градивни елементи се състоят от 6 x 6 = 36 малки квадратчета, което има смисъл, тъй като 6 е най-малкото общо кратно на 2 и 3. Симетрията се получава от повтарящите се копия на квадрат 5 x 5 с хубава четирикратна симетрия.
Следващата фигура отива една стъпка напред, присвоявайки червено за числата, които са кратни на 2, оранжево за числата, които са кратни на 3 и жълто за числата, които са кратни на 4. Ако в клетката е кратно на две от тези числа (например 6 = 2 x 3), се слага цветът на по-голямото от тези две числа (оранжево в случая). Ще се придържаме към тази конвенция за останалата част от тази статия.
Този път основните градивни елементи съдържат 12 x 12 клетки, защото 12 е най-малкото общо кратно на 2, 3 и 4. Симетрията идва от повтарящи се копия на един квадрат 11 x 11, който съдържа девет малки 3 x 3 квадратчета, които заедно създават приятна четирикратна симетрия.
Можем да продължим да играем тази игра до безкрай. Какво модели откривате? Можете ли да намерите всички оси на огледална симетрия? Какъв трябва да бъде размерът на основните (повтарящи се) градивни елементи на симетрия във всеки случай?
Кликнете върху снимките, за да видите по-голяма версия:
Кратни на непоследователни числа
Сега ще използваме няколко непоследователни стойности k. В следващата фигура се използва синьо за числата, които са кратни на 6 и зелено за числата, които са кратни на 9.
(Кликнете върху снимката, за да видите по-голяма версия.)
Основните градивни елементи вече ще се състоят от 18 x 18 = 324 малки квадратчета, тъй като 18 е най-малкото общо кратно на 6 и 9. Допълнителните симетрии на деветте 5 x 5 квадратчета, които съставят квадратите 17 x 17 са приятна изненада. Интересно има ли математическо обяснение за това?
Ето още няколко модела за радост на окото. Всичките са случаи на оцветени кратни на непоследователни числа. Кои са те?
Кликнете върху снимките, за да видите по-голяма версия:
Остатъци
И накрая цветовете на клетките са в зависимост от техния остатък по отношение на някакво число k. Например кратните на 5 са черни, числата с остатък 1 при делене на 5 ще бъдат зелени, числата с остатък 2 - червени, числата с остатък 3 - лилави и числата с остатък 4 - жълти. Получава се следната фигура:
Кликнете върху снимките, за да видите по-голяма версия:
Открихме някои от симетриите, че се крият в таблицата за умножение на положителни числа. Лесно се създават тези модели (например, с помощта на Excel) и всички могат да бъдат обяснени без много затруднения помощта на средно аритметично на цели числа и критериите за делимост. Показаните симетрии внасят нов нюанс в математиката.
Тези изображения и други, създадени по подобен начин, хвърлят мост между математиката и изкуството.
Страница на статията : 0102
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари