
Лауреатите на тазгодишната нобелова награда за физика Ален Аспект, Джон Клаузер и Антон Цайлингер с помощта на новаторски експерименти демонстрират потенциала за изследване и контрол на частици, които се намират във вплетено състояние.
Това, което се случва с едната частица от вплетена двойка, определя какво се случва с другата, дори ако те са твърде далеч една от друга, за да си влияят взаимно.
Разработването на експериментални инструменти от лауреатите постави основите на нова ера в квантовите технологии.
Основите на квантовата механика не са само теоретичен или философски въпрос. В момента се провеждат интензивни изследвания и разработки за използване на специалните свойства на отделните системи частици за конструиране на квантови компютри, подобряване на измерванията, изграждане на квантови мрежи и установяване на сигурна квантова криптирана комуникация.
Много от приложенията се основават на това как квантовата механика позволява на две или повече частици да съществуват в общо състояние, независимо от това на какво разстояние се намират една от друга. Това се нарича квантово вплитане и е един от най-дискутираните елементи на квантовата механика още от формулирането на теорията. Алберт Айнщайн говори за призрачно действие на разстояние, а Ервин Шрьодингер казва, че това е най-важната черта на квантовата механика.
Тазгодишните лауреати са изследвали тези вплетени квантови състояния и техните експерименти са поставили основите на революцията, която в момента се извършва в квантовите технологии.
Далеч от ежедневния опит
Когато две частици се намират в заплетени квантови състояния, някой, който измерва някакво свойство на едната частица, може веднага да определи резултата от еквивалентно измерване на другата частица, без да е необходимо да проверява.
На пръв поглед това може би не е толкова странно. Ако мислим за топки вместо за частици, можем да си представим експеримент, при който черна топка се изпраща в една посока, а бяла - в обратната. Наблюдател, който хване топката и види, че тя е бяла, може веднага да каже, че топката, която е пътувала в другата посока, е черна.
Това, което прави квантовата механика толкова специална, е, че нейните еквиваленти на топките нямат определени състояния, докато не бъдат измерени. Сякаш и двете топки са сиви, докато някой не погледне една от тях. Тогава тя може произволно да приеме или цялото черно, или изцяло бяла, а другата топка веднага се оцветява в противоположния цвят.
Но как е възможно да се разбере, че в началото всяка от топките не е имала определен цвят? Дори и да са изглеждали сиви, може би вътре в тях е имало скрит етикет, който казва какъв цвят трябва да придобият, когато някой ги погледне.
Съществува ли цвят, когато никой не го гледа?
Вплетените двойки в квантовата механика могат да се сравнят с машина, която изхвърля топки с противоположни цветове в противоположни посоки. Когато Боб хване една топка и види, че тя е черна, той веднага разбира, че Алис е хванала бяла топка. В теорията, която използва скрити променливи, топките винаги съдържат скрита информация за това какъв цвят да покажат. Квантовата механика обаче казва, че топките са били сиви, докато някой не ги погледне, тогава едната на случаен принцип става бяла, а другата черна. Неравенствата на Бел показват, че съществуват експерименти, които могат да разграничат тези случаи. Такива експерименти са доказали, че описанието на квантовата механика е правилно.

Важна част от изследванията, за които е присъдена тазгодишната Нобелова награда за физика, е теоретично разбиране, наречено неравенства на Бел. Неравенствата на Бел позволяват да се направи разлика между неопределеността на квантовата механика и алтернативно описание, използващо скрити инструкции или скрити променливи.
Експериментите показват, че природата се държи така, както е предсказано от квантовата механика. Топките са сиви, без скрита информация, и случайността определя коя от тях става черна и коя - бяла в даден експеримент.
Най-важният ресурс на квантовата механика - вплетените квантови състояния - крият потенциал за нови начини за съхраняване, пренасяне и обработка на информация.
Интересни неща се случват, ако частиците в една заплетена двойка се движат в противоположни посоки и след това една от тях срещне трета частица по такъв начин, че те станат вплетени.
Тогава те преминават в ново споделено състояние. Третата частица губи своята идентичност, но нейните първоначални свойства вече са били прехвърлени на самостоятелната частица от първоначалната двойка. Този начин на прехвърляне на неизвестен квант състояние от една частица в друга се нарича квантова телепортация. Този вид експеримент е проведен за първи път проведен през 1997 г. от Антон Цайлингер и неговите колеги.
Забележително е, че квантовата телепортация е единственият начин за прехвърляне на квантова информация от една система в друга, без да се губи каквато и да е част от нея. Абсолютно невъзможно е да се измерят всички свойства на една квантова система и след това да се изпрати информацията на получател, който иска да възстанови системата. Това е така, защото квантовата система може да съдържа едновременно няколко версии на всяко свойство, като всяка версия има определена вероятност да се появи по време на измерването. Веднага след като измерването бъде извършено, остава само една версия, а именно тази, която е била прочетена от измервателния уред. Останалите са изчезнали и е невъзможно някога да узнаем нещо за тях. Въпреки това напълно неизвестни квантови свойства могат да бъдат пренесени с помощта на квантова телепортация и да се появят непокътнати в друга частица, но с цената на това да бъдат унищожени в първоначалната частица.
След като това е доказано експериментално, следващата стъпка е да се използват две двойки вплетени частици. Ако по една частица от всяка двойка се събере по определен начин, незасегнатите частици от всяка двойка могат да се вплетат, въпреки че никога не са били в контакт една с друга. Тази размяна на вплитане е демонстрирана за първи път през 1998 г. от изследователската група на Антон Цайлингер.
Вплетените двойки фотони, частици светлина, могат да се изпращат в противоположни посоки през оптични влакна и да функционират като сигнали в квантова мрежа. Вплитането между две двойки дава възможност да се увеличат разстоянията между възлите в такава мрежа. Съществува ограничение за разстоянието, на което фотоните могат да бъдат изпратени през оптично влакно, преди да бъдат погълнати или да загубят свойствата си. Обикновените светлинни сигнали могат да бъдат усилвани по пътя, но това не се случва при вплетените двойки.
Усилвателят трябва да улови и измери светлината, което нарушава вплитането. Размяната на вплитането обаче означава, че е възможно да се изпрати оригиналното състояние по-нататък, като по този начин то се пренася на по-големи разстояния, отколкото би било възможно иначе.
Вплетени частици, които никога не са се срещали
Две двойки вплетени частици се излъчват от различни източници. По една частица от всяка двойка се събира по специален начин, който ги вплита. След това другите две частици (1 и 4 на схемата) също се вплитат. По този начин две частици, които никога не са били в контакт, могат да станат вплетени.

Този напредък се дължи на многогодишно развитие. Началото бе поставено с невероятното прозрение, че квантовата механика позволява една квантова система да бъде разделена на части, които са отделени една от друга, но все пак действат като едно цяло.
Това противоречи на всички обичайни представи за причината и следствието и за природата на реалността. Как може нещо да бъде повлияно от събитие, случващо се някъде другаде, без до него да е достигнал някакъв сигнал от него? Сигналът не може да се движи по-бързо от светлината - но в квантовата механика не изглежда да има нужда от сигнал, който да свързва различните части на една разширена система.
Алберт Айнщайн смята това за неосъществимо и изследва този феномен заедно с колегите си Борис Подолски и Натан Розен. През 1935 г. те представят своите разсъждения: изглежда, че квантовата механика не предоставя пълно описание на реалността. Това се нарича парадокс на EPR, по името на инициалите на изследователите.
Въпросът бил дали може да има по-пълно описание на света, в което квантовата механика е само една част. Това би могло да стане например чрез частици, които постоянно носят скрита информация за това какво ще покажат като резултат от даден експеримент. Тогава всички измервания показват свойствата, които съществуват точно там, където се извършват измерванията. Този тип информация често се нарича локални скрити променливи.
Северноирландският физик Джон Стюарт Бел (1928-1990 г.), който работи в ЦЕРН, Европейската лаборатория по физика на елементарните частици, се вглежда по-отблизо в проблема. Той открива, че съществува един вид експеримент, който може да определи дали светът е чисто квантовомеханичен, или може да има друго описание със скрити променливи. Ако неговият експеримент се повтори многократно, всички теории със скрити променливи ще показват корелация между резултатите, която трябва да е по-ниска или най-много равна на определена стойност. Това се нарича неравенство на Бел.
Квантовата механика обаче може да наруши това неравенство. Тя предсказва по-високи стойности на корелацията между резултатите, отколкото е възможно чрез скритите променливи.
Джон Клаузер започва да се интересува от основите на квантовата механика още като студент през 60-те години на миналия век. Той не можел да се отърси от идеята на Джон Бел, след като прочел за нея, и в крайна сметка заедно с трима други изследователи успява да представи предложение за реалистичен тип експеримент, който може да се използва за проверка на неравенството на Бел.
Експериментът включва изпращане на двойка вплетени частици в противоположни посоки. На практика се използват фотони, които имат свойство, наречено поляризация. Когато частиците се излъчват, посоката на поляризация не е определена и единственото, което е сигурно, е, че частиците имат успоредна поляризация.
Това може да се изследва с помощта на филтър, който пропуска поляризация, ориентирана в определена посока (вж. схемата "Експерименти с неравенствата на Бел", по-долу). Това е ефектът, използван в много слънчеви очила, които блокират светлината, поляризирана в определена равнина, например от отражения от водна повърхност. Ако и двете частици в експеримента се изпратят към филтри, ориентирани в една и съща равнина, например вертикално, и едната се промъкне през тях - тогава и другата ще премине. Ако те са разположени под прав ъгъл една спрямо друга, едната ще бъде спряна, а другата ще премине. Трикът е да се измерва с филтри, разположени в различни посоки под наклонени ъгли, тъй като тогава резултатите могат да варират: понякога се промъкват и двете, понякога само едната, а понякога нито една. Колко често и двете частици преминават през филтъра, зависи от ъгъла между филтрите.
Квантовата механика води до корелация между измерванията. Вероятността една частица да премине зависи от ъгъла на филтъра, който проверява поляризацията на партньора ѝ от противоположната страна на експерименталната постановка. Това означава, че резултатите от двете измервания, при някои ъгли, нарушават неравенството на Бел и имат по-силна корелация, отколкото биха имали, ако резултатите се управляваха от скрити променливи и бяха предварително определени още при излъчването на частиците.
Нарушено неравенство
Джон Клаузер веднага започва работа по провеждането на този експеримент. Той конструира апарат, който излъчва два вплетени фотона едновременно, всеки от които е насочен към филтър, който проверява тяхната поляризация. През 1972 г., заедно с докторанта Стюарт Фридман (1944-2012), той успява да покаже резултат, който е явно нарушение на неравенството на Бел и е в съгласие с предсказанията на квантовата механика. През следващите години Джон Клаузер и други физици продължават да обсъждат експеримента и неговите ограничения. Едно от тях е, че експериментът като цяло е неефективен, както по отношение на производството, така и на улавянето на частици. Измерването също така е било предварително зададено, като филтрите са били под фиксирани ъгли. Поради това имало пропуски, при които наблюдателят можел да постави под въпрос резултатите: ами ако експерименталната настройка по някакъв начин е избрала частиците, които са имали силна корелация, и не е открила останалите? Ако е така, частиците все още биха могли да носят скрита информация.
Премахването на тази конкретна вратичка е било трудно, тъй като вплетените квантови състояния са много крехки и трудни за управление; необходимо е да се работи с отделни фотони. Френският докторант Ален Аспект не се уплашил и построил нова версия на установката, която усъвършенствал в продължение на няколко итерации. В своя експеримент той може да регистрира фотоните, които преминават през филтъра, и тези, които не преминават. Това означава, че могат да бъдат засечени повече фотони и измерванията са по-добри.
Във финалния вариант на тестовете си той също така успява да насочи фотоните към два различни филтъра, които са поставени под различен ъгъл. Новото е механизъм, който превключва посоката на вплетените фотони, след като те са създадени и излъчени от източника си. Филтрите се намират само на шест метра разстояние, така че превключването е трябвало да стане за няколко милиардни части от секундата. Ако информацията за това до кой филтър ще пристигне фотонът е повлиявала на начина, по който той е бил излъчен от източника, той не би пристигнал до този филтър. Също така информацията за филтрите от едната страна на експеримента не би могла да достигне до другата страна и да повлияе на резултата от измерването там.
По този начин Ален Аспект затворил важен пропуск и дал много ясен резултат: квантовата механика е правилна и няма скрити променливи.
Ерата на квантовата информация
Тези и други подобни експерименти поставят основите на сегашните интензивни изследвания в областта на квантовата информация. Възможността да манипулираме и управляваме квантовите състояния и всички техни пластове от свойства ни дава достъп до инструменти с неочакван потенциал. Това е основата на квантовите изчисления, преноса и съхранението на квантова информация и алгоритмите за квантово криптиране. В момента се използват системи с повече от две частици, които са вплетени, които Антон Цайлингер и колегите му първи изследват.
Експерименти с неравенствата на Бел

Джон Клаузер използва калциеви атоми, които могат да излъчват вплетени фотони, след като ги освети със специална светлина. Той поставя филтър от двете страни, за да измерва поляризацията на фотоните. След поредица от измервания той успява да докаже, че те нарушават неравенството на Бел.

Ален Аспект развива този експеримент, като използва нов начин за възбуждане на атомите, така че те да излъчват вплетени фотони с по-голяма скорост. Той също така може да превключва между различни настройки, така че системата да не съдържа никаква предварителна информация, която би могла да повлияе на резултатите.
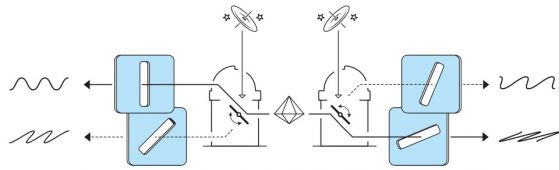
Кредит: ©Johan Jamestad/The Royal Swedish Academy of Sciences
По-късно Антон Цайлингер провежда още тестове на неравенствата на Бел. Той създава вплетени двойки фотони, като облъчва с лазер специален кристал, и използва случайни числа, за да превключва между настройките на измерването. При един от експериментите използва сигнали от отдалечени галактики, за да контролира филтрите и да гарантира, че сигналите не могат да си влияят взаимно.
Тези все по-усъвършенствани инструменти се доближават все повече до реалистични приложения. Вече са демонстрирани вплетени квантови състояния между фотони, изпратени през десетки километри оптично влакно, както и между сателит и наземна станция. За кратко време изследователите от цял свят откриват много нови начини за използване на най-мощното свойство на квантовата механика.
Първата квантова революция ни даде транзистори и лазери, но сега навлизаме в нова ера благодарение на съвременните инструменти за манипулиране на системи от заплетени частици.
Нобеловатa награда за физика за 2022 година е присъдена на Ален Аспект (Alain Aspect), Джон Клаузер (John Clauser) и Антон Цайлингер (Anton Zeilinger) "за експериментите им с вплетени фотони, които установяват нарушаването на неравенствата на Бел и за пионерната им работа в квантовата информатика"
Изтoчник: How entanglement has become a powerful tool, The Royal Swedish Academy of Sciences
Още по темата

Физика
Нобеловата награда за физика 2022 е за пионерни изследвания в квантовата механика (видео)

Физика
Квантово вплитане на много атоми е наблюдавано за първи път

Физика
Квантовото вплитане вече се наблюдава директно в по-голям макроскопичен мащаб



















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews