
Плоският пъзел (облицовка) с десетки или стотици еднакви парчета може да изглежда малко скучно и предсказуемо.
Но коя е най-интересната форма, която можем да използваме, за да получим най-необичайния дизайн и най-голямо разнообразие?
За да бъде визуално по-интересно, можем да използваме фигура без прави ръбове - само с криви.
Насока може да ни даде Тим Лексен (Tim Lexen) американски машинен инженер, който повече от 40 години се занимава с научноизследователската дейност и е любител на елегантните решения. И така какво може да ни помогне да започнем?
- Нека използваме дъги от кръгове, всичките с еднакъв радиус на единица дължина. По-нататък няма да говорим за дължини, а само за ъгли. Това са ъглите на дъгите и на върховете. За добра облицовка тези ъгли трябва да бъдат делители на 360° като например кратни на 12° или 15° са „приемливи“ ъгли.
- Тъй като дъгите трябва да съвпадат, трябва да има толкова вдлъбната дъга, колкото изпъкнала дъга.
- Ще разгледаме фигури, които могат да съставят периодични облицовки - тоест, като плочките се повтарят, но търсим и плочки, които си пасват след завъртане, с колкото повече опции, толкова по-добре.
- Да кажем, че сме свободни да използваме огледални изображения на елемента. В началото това може да не изглежда от полза при симетрични форми, но може да стане важно по-късно при по-сложни форми и облицовки.
Да започнем с квадрат
Най-просто е да започнем с квадрат, тъй като можем просто да заменим страните с две вдлъбнати и две изпъкнали дъги и да получим облицовка въз основа на съседни квадратчета, както е показано по-долу. Можем да започнем с дъги от 90 °, които биха могли да впишат квадрата. Долната форма отдолу ще се покаже отново. Използва се от векове. Тим Лексен нарича фигурата "Рак".

Ъгълът на дъгата може да бъде всякаква стойност до 180°, както е показано по-долу.

Подобни резултати могат да бъдат постигнати, ако се започне с ромб, но с по-изкривен изглед:

Плочки с основа триъгълник
По-трудно е да започнем с триъгълник заради това, че има трите страни. Не можем просто да заменим трите страни на равностранен триъгълник с еднакви дъги, тъй като няма да можем да получим едно и също количество изпъкнали и вдлъбнати дъги.
Правоъгълен равнобедрен триъгълник с ъгъл 45° може лесно да се преобразува, като се постави дъга от 180° върху хипотенузата и дъга от 90° на двете по-малки страни. Така ще се получи плочка "Рак" отново.
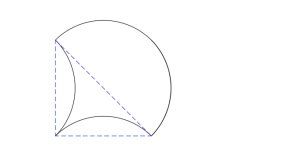
Всеки правоъгълен триъгълник може да бъде превърнат във форма на плочка, като поставим изпъкнала дъга от 180° върху хипотенузата и вдлъбнати дъги със същия радиус на всяка от по-малките страни. Това е така, защото всеки правоъгълен триъгълник може да бъде вписан в полукръг.

Тази форма може да оформя периодични плочки, а някои специални случаи - като преобразуване от правоъгълни триъгълници с ъгли 45 ° и 30 ° / 60 ° - водят до форми с приемливи ъгли, които също могат да облицоват със завъртане. Но с всички останали правоъгълни триъгълници не можем лесно да получим ъглите, които са ни нужни.
С пълен кръг
Ако започнем с цял кръг, ще трябва да заменим половината обиколка с вдлъбнати дъги. Можем да започнем със създаването на две вдлъбнати дъги от 90°, или една срещу друга или една до друга - и да получим двете еднакви фигури, които получихме първоначално, използвайки квадратчетата.
Можем да използваме и три вдлъбнати дъги от 60°. Това може да се направи по трите механизма, показани по-долу.

Тези форми могат да бъдат направени и с помощта на шестоъгълник като основа.
Формата вдясно по-горе - с трите съседни вдлъбнати изреза - може да бъде модифицирана с други размери или вдлъбнати дъги. Ако искаме да останем симетрични, можем да използваме различни комбинации от вдлъбнати дъги на обща стойност 180°, както е показано по-долу. Всички те ще могат да се наредят по един и същи периодичен начин. Ако долният среден изрез се намали до нула, ще имаме само две вдлъбнати дъги от 90° - ще се получи плочка "Рак" отново.

Този подход с три вдлъбнати изреза в долната половина също може да се използва при основа с форма на леща. Лещата се създава като вземем една дъга (до 180 градуса) и я копираме огледално с ос, определена от двете й крайни точки. Това е по-общ случай на кръг. Както направихме с кръга, можем да направим подобни периодични облицовки с три вдлъбнати изреза, ограничени от една от дъгите.

Всички форми, описани досега, се подреждат предсказуемо и периодично, макар и с широк диапазон от възможни ъгли. Някои от тях могат да се съчетаят по по-сложни начини, с въртене и повече възможности за облицовка. Как можем да получим най-голяма гъвкавост от една форма или още по-добре, от семейство форми?
Трифокусните лещи
Семейството форми с най-голяма гъвкавост има три страни. Но не се построява от триъгълник, а по-скоро започва с желаните ъгли на върховете или дъги в рамките на формата на лещата.
Да кажем, че искаме форма, подобна на триъгълник, с използваемите ъгли на върховете от 30° и 60°. Това също ще бъдат ъглите на двете вдлъбнати дъги. Можем да започнем конструкцията с тях, но е по-лесно да започнем с широкоъгълната леща, която ще бъде сумата от тях, или 90°. Затова правим дъга от 90° и обръщаме копието й огледално, за да направим фигура на леща. След това маркираме двете по-малки дъги - точката, където се срещат на огледалната дъга - и огледално обръщаме всяка от тях около крайните й точки.
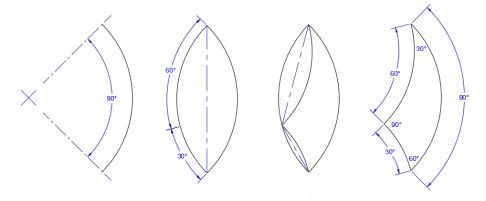
Получената форма позволява изненадваща гъвкавост за облицовка.
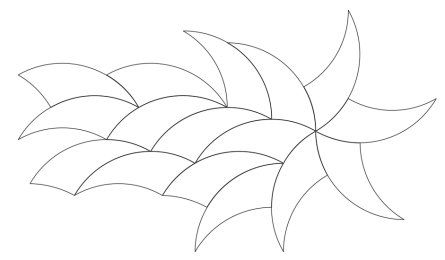
Голямото предимство при този подход е, че първо избираме ъглите на върховете, а после останалото. Ако искаме да изградим облицовка около 5-лъчеви звезди, можем да изберем малки ъгли от, да речем, 36° и 72°.
Ако приемем, че използваме разумни ъгли, тази конструкция и облицовка работи за всеки голям ъгъл до 180 ° и всяко пропорционално разпределение на двете по-малки дъги. Върхът на ъгъла срещу голямата изпъкнала дъга винаги е добавката (разлика от 180 °) на голямата дъга. А по-малките върхови ъгли винаги са същите като вдлъбнатите дъги.
Горният подход ни позволява да направим широка гама от форми, със сложни и разнообразни облицовки, които са радиални, периодични или непериодични, или някаква комбинация от тях. Това ново семейство форми можем да наречем тридъгови.
Източник: Tiling with One Arc-Sided Shape, Tim Lexen






















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години
Peter Petrov
След многократни експлозии нов тест за мегаракетата на Мъск
поп Дръвчо
Гледайте за първи път на живо как новооткритият "междузвезден посетител" 3I/ATLAS се устремява към нас