Какво откри Мирзахани, жената с най-престижната награда за математика (видео)

Новината за кончината на Мариам Мирзахани, първата и единствена жена, наградена с медала "Фийлдс", обходи всички медии, но никой не обясни областта, в която се е занимавала.

И макар всички да бяха единодушни, че е работила върху сложни проблеми в математиката, колегите й разказват, че самата Мирзахани " с думите и действията си е показала, че всякакви математически идеи могат да бъдат разбрани, ако се вложи достатъчно постоянство в задачата".

"Тя не беше звездата на лекциите си, единствените звезди бяха математическите й идеи. Тя говореше спокойно и ясно и излъчваше дълбока наслада от процеса" - си спомня Мойра Час (Moira Chasе), доцент по математика в университета "Стоуни Брук", на страницата на Quanta magazine.

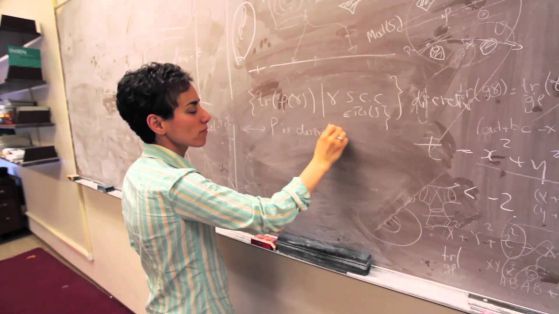^{Снимка: Jan Vondrák}

За да надзърнем в математическия свят на Мирзахани, можем да започнем с нещо познато - земята под краката ни. Въпреки добрите ни познания за формата на Земята, когато се разхождаме по нея я чувстваме плоска. Всяко парченце от Земята много прилича на малка част от двумерна равнина.

Повърхността на Земята е пример за математическа повърхнина - форма, която може да бъде покрита с малки застъпващи се парченца, всяко от които може да се приеме за парче равнина.

Сферата е само един пример за математическа повърхнина. Други примери могат да бъдат повърхнините на портокал или футболна топка, или поничка.

Но колко вида различни повърхнини имаме? На пръв поглед изглежда, че са безброй. Всеки портокал има свои характерни неравности и всеки картоф - собствена форма, така че можем да получим невероятно голям брой различни повърхнини дори само за плодове и зеленчуци.

Но ако си затворим очите за неравностите и дребните колебания във формата, нещата стават много по-прости. Можем да приемем, че две повърхнини са едни и същи, ако могат да бъдат деформирани от една в друга без рязане или лепене. Тогава всички портокали и футболни топки ще съответстват на една и съща форма - сфера. По същия начин всички понички в света отговарят на гладката и равномерна форма на пръстен, наречена тор. Тези два класа обекти по същество обаче са различни един от друг, тъй като няма начин да се превърне една сфера в тор без рязане или лепене - няма как да се създаде дупка.

Тор

И как чаша за кафе се превръща в тор и обратното

Оказва се, че броят на дупките е това, което определя повърхнината, ако игнорираме деформациите. Всяка повърхнина, която е без край (това, че няма край означава, че можете да паднете, ако се разхождате по нея и може да бъде покрита с краен брой парчета) и ориентируема (има външна и вътрешна страна) може да се деформира или в сфера, или в тор, или в изпъкналост с две дупки или три дупки или четири дупки, и така нататък, но това са единствените възможности. Като позволихме деформациите, ние превърнахме объркващия паноптикум от повърхнини в изчистено семейство, в което всяка повърхнина се характеризира с броя на дупките, които има.

^{Източник: laerne.github.io}

Този абстрактен начин на мислене за повърхнините е свойствен за топологията, една от областите в която работи Мариам.

Мирзахани разглежда повърхности с определен вид геометрия, известни като хиперболични повърхнини. Най-късият път между две точки на повърхността, се определя от специална линия на повърхността, наречена геодезична. Самолетите следват подобни геодезични линии, определени от сферичната геометрия на повърхността на Земята, траекторията на полетите следват част от геодезичните линии като най-късо разстояние между летищата.

^{Сферична, хиперболична и евклидова (плоска) повърхнина (Източник: NASA)}

Всички геодезични линии върху повърхност с сферична геометрия са затворени, като линиите на паралелите и екватора на земната повърхност. Но геодезичните линии могат да бъдат по-сложни за по-сложните повърхнини: например, ако повърхността е на тороид с две дупки, затворената геодезическа линия може да обикаля около една от дупките.

Един въпрос, който можете да си зададете, е: ако имате дадена дължина L, колко затворени геодезични линии има на една математическа повърхност с дължина L или по-къси?

Колкото е по-голяма дължината L, толкова повече затворени геодезични линии с дължина по-малка или равна на L се очаква да има, но колко бързо нараства бройката? Отговорът, който е известен от повече от 50 години, е много чист. Броят на затворените геодезични линии с дължина по-малка или равна на L нараства експоненциално с L , всъщност расте с израза:

e ^L / L,

където e = 2.71828... е известна математическа константа. (Този резултат носи радост в сърцето на всеки математик, тъй като има аналог в съвсем друга област на математиката: той е много подобен на теоремата за разпределението на простите числа, която дава броя на прости числа по-малки или равни на определено число.)

Едно нещо, което трябва да се отбележи за този резултат е, че той не зависи от това какъв тип хиперболична повърхнина се разглежда - по-специално, не зависи от броя на дупките, които има. Но Мирзахани установи, че това се променя, ако броим не всички затворени геодезични линии, но само тези, които не се пресичат (например да пренебрегнем затворенитв геодезични линии, които приличат на осморки). Оказва се, че сега броят, чиято дължина е по-малка или равна на L расте не експоненциално, а много по-бавно, асимптотично към:

L^6g-6 

където g е броят на дупките на повърхнината. 

Изглежда просто, но точно това го прави специално - резултати с такава елегантна простота, които все пак много трудно се доказват, са чудесна награда в математиката. И това, което е още по-хубаво, прозренията на Мирзахани, докато тя разработваше доказването на този резултат, доведоха до отговорите на други отворени въпроси. Това е много ползотворен резултат. И както самата Мирзахани казва: "Това не се отнася само за въпроса, а и за начина, по който се решава".

^{ICM 2014 в Сеул, когато на Мирзахани бе връчен медала "Фийлдс".}

Когато Мирзахани е още дете и проявява интерес към математиката, това става в много трудни времена - по време на войната в Иран. "Това бяха трудни времена", разказва тя, "но бях част от щастливото поколение, когато станах тийнейджър, нещата се стабилилизираха". Тя се премества в САЩ, за да следва докторантурата си в Харвардския университет, а след това става професор в Университетите Принстън и Станфорд. Освен че е първата и до момента единствената жена носител на медала "Фийлдс", а също така е и първият иранец, получил отличието.

Животът на Мирзахани е едно важно напомняне, че математиката не се интересува кой си, от къде си, на какъв език говориш, цвета на кожата ти или от какъв пол си - тя е универсален език, който принадлежи на всички нас.

Трагично е, че загубихме такъв блестящ математически ум толкова млад.

Източници:

The mathematical work of Maryam Mirzakhani

Remembering Maryam Mirzakhani, The Plus Team 

The Beautiful Mathematical Explorations of Maryam Mirzakhani, Moira Chas

Още по темата

15/07/2017

Математика

Почина Мариам Мирзахани, първата жена, получила най-престижната награда за математика, медала „Фийлдс“

13/06/2017

Математика

Скромният гений Григорий Перелман - математикът, решил задачата на хилядолетието

25/12/2014

Математика

Хипотезата на Поанкаре - последната решена нерешима задача