

–Ę–į–Ī–Ľ–ł—Ü–ł—ā–Ķ –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ī–į—ā–ł—Ä–į—ā –ĺ—ā –≤–į–≤–ł–Ľ–ĺ–Ĺ—Ü–ł—ā–Ķ –ĺ—ā –Ņ—Ä–Ķ–ī–ł –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 4000 –≥–ĺ–ī–ł–Ĺ–ł. –Ě–į–Ļ-—Ä–į–Ĺ–Ĺ–ł—ā–Ķ –ī–Ķ—Ā–Ķ—ā–ł—á–Ĺ–ł –Ņ—Ä–ł–ľ–Ķ—Ä–ł —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į—ā –≤ –ö–ł—ā–į–Ļ –ĺ–ļ–ĺ–Ľ–ĺ 300 –≥. –Ņ—Ä. –Ĺ. –Ķ., –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ł—Ä–į–Ĺ–ł —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –Ī–į–ľ–Ī—É–ļ–ĺ–≤–ł –Ľ–Ķ–Ĺ—ā–ł –ł –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –∑–į —É–ľ–Ĺ–ĺ–∂–į–≤–į–Ĺ–Ķ –Ĺ–į —Ü–Ķ–Ľ–ł –ł –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į –ī–ĺ 99,5. –ē–ī–ł–Ĺ –ĺ—ā –Ĺ–į–Ļ-—Ä–į–Ĺ–Ĺ–ł—ā–Ķ –Ņ—Ä–ł–ľ–Ķ—Ä–ł, –ļ–ĺ–ł—ā–ĺ –Ī–ł—Ö–ľ–Ķ —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–Ľ–ł, –Ķ –Ę–į–Ī–Ľ–ł—Ü–į—ā–į –Ĺ–į –ü–ł—ā–į–≥–ĺ—Ä, –≤–ļ–Ľ—é—á–Ķ–Ĺ–į –ĺ—ā –Ě–ł–ļ–ĺ–ľ–į—Ö –≤ –Ĺ–Ķ–≥–ĺ–≤–ĺ—ā–ĺ "–í—ä–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –≤ –į—Ä–ł—ā–ľ–Ķ—ā–ł–ļ–į—ā–į" –ĺ—ā–Ņ—Ä–Ķ–ī–ł –ĺ–ļ–ĺ–Ľ–ĺ 100 –≥. —Ā–Ľ. –Ĺ.–Ķ.
–Ē–Ĺ–Ķ—Ā –≤ —É—á–ł–Ľ–ł—Č–Ķ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ķ —Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ, –ļ–ĺ–Ķ—ā–ĺ —É—á–Ķ–Ĺ–ł—Ü–ł—ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā, –∑–į –ī–į –Ĺ–į—É—á–į—ā —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —á—Ä–Ķ–∑ –Ĺ–į–ł–∑—É—Ā—ā—Ź–≤–į–Ĺ–Ķ. –í—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –Ĺ—Ź–ļ–ĺ–ł —Ā–ľ—Ź—ā–į—ā, —á–Ķ –ĺ–≤–Ľ–į–ī—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ķ —Ā–į–ľ–ĺ –Ņ–ĺ —Ā–Ķ–Ī–Ķ —Ā–ł –Ņ–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł–Ķ, –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā —ā—Ź –ī–į–≤–į –Ĺ–į —É—á–Ķ–Ĺ–ł—Ü–ł—ā–Ķ –∑–ī—Ä–į–≤–į –ĺ—Ā–Ĺ–ĺ–≤–į –∑–į –Ņ–ĺ–Ľ–į–≥–į–Ĺ–Ķ –Ĺ–į –ĺ—Č–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —ā—É—Ö–Ľ–ł—á–ļ–ł. –Ě–Ķ–ļ–į —Ā–Ķ –Ņ–ĺ—ā–ĺ–Ņ–ł–ľ –≤ –Ņ–ĺ-–ī—ä–Ľ–Ī–ĺ–ļ–ł –≤–ĺ–ī–ł –ł –ī–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–ľ–Ķ –Ĺ—Ź–ļ–ĺ–ł —É–ī–ł–≤–ł—ā–Ķ–Ľ–Ĺ–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł, –ļ–ĺ–ł—ā–ĺ —Ä–į–∑–ļ—Ä–ł–≤–į—ā –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł—ā–Ķ, —Ā–ļ—Ä–ł—ā–ł –≤ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ.
–Ę—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł –ł –ļ–≤–į–ī—Ä–į—ā–ł
–í –ľ–ĺ—Ä–Ķ—ā–ĺ –ĺ—ā —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į —á–Ķ—Ä–≤–Ķ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ņ–ĺ –≥–Ľ–į–≤–Ĺ–ł—Ź (–ĺ—ā —Ā–Ķ–≤–Ķ—Ä–ĺ–∑–į–Ņ–į–ī –Ĺ–į —é–≥–ĺ–ł–∑—ā–ĺ–ļ) –ī–ł–į–≥–ĺ–Ĺ–į–Ľ –Ĺ–į —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ —Ā–į –ļ–≤–į–ī—Ä–į—ā–ł - –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į, –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ł –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ 2.

–Ę–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ —Ā—ä—Č–ĺ –Ĺ–ł –Ņ–ĺ–ļ–į–∑–≤–į –ł¬†—ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł —á–ł—Ā–Ľ–į. –Ę—Ä–ł—ä–≥—ä–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –Ķ —á–ł—Ā–Ľ–ĺ, –ļ–ĺ–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ķ–Ĺ–ĺ —á—Ä–Ķ–∑ —ą–į–Ī–Ľ–ĺ–Ĺ –ĺ—ā —ā–ĺ—á–ļ–ł, –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ł –≤ —Ä–į–≤–Ĺ–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ —Ā –Ķ–ī–Ĺ–į–ļ—ä–≤ –Ī—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł –ĺ—ā –≤—Ā—Ź–ļ–į —Ā—ā—Ä–į–Ĺ–į –Ĺ–į –Ķ–ī–Ĺ–į–ļ–≤–ĺ —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ķ–ī–Ĺ–į –ĺ—ā –ī—Ä—É–≥–į. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä:

–ü—ä—Ä–≤–ĺ—ā–ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –Ķ 1, –≤—ā–ĺ—Ä–ĺ—ā–ĺ –Ķ 1+2=3, —ā—Ä–Ķ—ā–ĺ—ā–ĺ –Ķ 1+2+3=6, —á–Ķ—ā–≤—ä—Ä—ā–ĺ—ā–ĺ 1+2+3+4=10 –ł —ā.–Ĺ.
–°—É–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —á–ł—Ā–Ľ–į—ā–į –≤—ä–≤ –≤—Ā—Ź–ļ–į –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į –Ĺ–į —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, –∑–į–Ņ–ĺ—á–≤–į—Č–į –ĺ—ā —Ä–Ķ–ī 1 –ł –ļ–ĺ–Ľ–ĺ–Ĺ–į 1, –Ĺ–ł –ī–į–≤–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ĺ–į –ļ–≤–į–ī—Ä–į—ā.

–°—É–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —á–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł—ā–Ķ –ľ–į—ā—Ä–ł—Ü–ł, –∑–į–Ņ–ĺ—á–≤–į—Č–ł –ĺ—ā —Ä–Ķ–ī 1 –ł –ļ–ĺ–Ľ–ĺ–Ĺ–į 1, –Ĺ–ł –ī–į–≤–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ĺ–į –ļ–≤–į–ī—Ä–į—ā.
–Ě–Ķ —Ā–į–ľ–ĺ —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā —Ä–į–∑–ļ—Ä–ł—ā–ł –≤ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —ā—Ź –ľ–ĺ–∂–Ķ –ī–į –Ĺ–ł –ī–į–ī–Ķ –ł –ļ–≤–į–ī—Ä–į—ā–ł –Ĺ–į —á–ł—Ā–Ľ–į—ā–į (—ā–ĺ—á–Ķ–Ĺ –ļ–≤–į–ī—Ä–į—ā).
–ź–ļ–嬆–ī–ĺ–Ī–į–≤–ł–ľ —Ä–Ķ–ī 0 –Ĺ–į–Ļ-–≥–ĺ—Ä–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–į 0 –ĺ—ā–Ľ—Ź–≤–ĺ –≤ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —ā—Ź –Ņ–į–ļ —Č–Ķ —Ā–ł –ĺ—Ā—ā–į–Ĺ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–į –ł —Č–Ķ –ĺ—Ā–ł–≥—É—Ä–ł —Ö—É–Ī–į–≤–į —Ä–į–ľ–ļ–į. –ź–ļ–ĺ –≤ —ā–į–ļ–į–≤–į¬†—ā–į–Ī–Ľ–ł—Ü–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ —Ā–Ķ –ĺ—Ü–≤–Ķ—ā—Ź—ā –≤ —Ā–ł–Ĺ—Ć–ĺ (–≤–ł–∂—ā–Ķ –Ņ–ĺ-–ī–ĺ–Ľ—É) –ļ—Ä–į—ā–Ĺ–ł –Ĺ–į —á–ł—Ā–Ľ–ĺ—ā–ĺ k, —Ā—É–ľ–į—ā–į –ĺ—ā —á–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į, –ĺ–≥—Ä–į–ī–Ķ–Ĺ–į –ĺ—ā —ā–Ķ–∑–ł —Ā–ł–Ĺ–ł –ļ—Ä–į—ā–Ĺ–ł, —Ā—ä—Č–ĺ –≤–ļ–Ľ—é—á–≤–į —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ.
–°—É–ľ–į—ā–į –ĺ—ā —á–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į –ľ–į—ā—Ä–ł—Ü–į –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į¬†(2m-1)(2n-1)T¬≤k-1, –ļ—ä–ī–Ķ—ā–ĺ m –ł n –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź –ľ—Ź—Ā—ā–ĺ—ā–ĺ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į –ľ–į—ā—Ä–ł—Ü–į, –ļ–į—ā–ĺ –Ī—Ä–ĺ–ł—ā–Ķ —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –ĺ—ā–≥–ĺ—Ä–Ķ –ł –ĺ—ā–Ľ—Ź–≤–ĺ, –ł Tk-1¬†–Ķ k-1-—ā–嬆–Ņ–ĺ —Ä–Ķ–ī —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ.

–ú–ĺ–∂–Ķ–ľ –ī–į –≤–ł–ī–ł–ľ, —á–Ķ —Ā—É–ľ–ł—ā–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł—ā–Ķ –ľ–į—ā—Ä–ł—Ü–ł, –ĺ–≥—Ä–į–ī–Ķ–Ĺ–ł –ĺ—ā —Ā–ł–Ĺ–ł—ā–Ķ –ļ—Ä–į—ā–Ĺ–ł –Ĺ–į –≥–Ľ–į–≤–Ĺ–ł—Ź (—Ā–Ķ–≤–Ķ—Ä–ĺ–∑–į–Ņ–į–ī –ļ—ä–ľ —é–≥–ĺ–ł–∑—ā–ĺ–ļ) –ī–ł–į–≥–ĺ–Ĺ–į–Ľ (–ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –≤ –∂—ä–Ľ—ā–ĺ –Ņ–ĺ-–ī–ĺ–Ľ—É) —Ā—ä—Č–ĺ —Ā–į –ļ–≤–į–ī—Ä–į—ā–ł –Ĺ–į —á–ł—Ā–Ľ–į. –Ę–ĺ–≤–į –ľ–ĺ–∂–Ķ –Ľ–Ķ—Ā–Ĺ–ĺ –ī–į —Ā–Ķ –ī–ĺ–ļ–į–∂–Ķ, –ļ–į—ā–ĺ —Ā–Ķ –≤–∑–Ķ–ľ–Ķ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–į—ā–į —Ą–ĺ—Ä–ľ—É–Ľ–į –∑–į —Ā—É–ľ–į—ā–į –ĺ—ā —Ā—ā–į—ā–ł—Ź—ā–į –ł —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł. –©–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–ľ–Ķ —Ā–į–ľ–ĺ m¬†–≤—ä–≤ —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į, –∑–į—Č–ĺ—ā–ĺ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ–į—ā–į –ł —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–į—ā–į –Ņ–ĺ–∑–ł—Ü–ł—Ź —Ā–į –Ķ–ī–Ĺ–į–ļ–≤–ł.
(2m-1)(2m-1)T2k-1 = ((2m-1)Tk-1)2
–†–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ł –ļ–≤–į–ī—Ä–į—ā–ł
–ź–ļ–ĺ –Ĺ–į–≤–Ľ–Ķ–∑–Ķ–ľ –≤ –ī—Ä—É–≥–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł –ľ–į—ā—Ä–ł—Ü–ł —Ā —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ —Ä–į–∑–ľ–Ķ—Ä –ł –≥–Ķ–ĺ–≥—Ä–į—Ą–ł—Ź –≤ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, –ľ–ĺ–∂–Ķ–ľ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł–ľ –Ņ–ĺ–≤–Ķ—á–Ķ –ļ–≤–į–ī—Ä–į—ā–ł¬†–Ĺ–į —á–ł—Ā–Ľ–į. –ö–≤–į–ī—Ä–į—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į, –ļ–ĺ—Ź—ā–ĺ –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā –≥–Ľ–į–≤–Ĺ–ł—Ź (–ĺ—ā —Ā–Ķ–≤–Ķ—Ä–ĺ–∑–į–Ņ–į–ī –ļ—ä–ľ —é–≥–ĺ–ł–∑—ā–ĺ–ļ) –ī–ł–į–≥–ĺ–Ĺ–į–Ľ, –ł–∑–≥–Ľ–Ķ–∂–ī–į –≤–ł–Ĺ–į–≥–ł –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ĺ –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –≤—ä–∑ –ĺ—Ā–Ĺ–ĺ–≤–į –Ĺ–į —Ā—É–ľ–į—ā–į –ĺ—ā¬†–ĺ–Ī—Č–ł—ā–Ķ¬†–Ĺ–ĺ–ľ–Ķ—Ä–į –Ĺ–į –ļ–ĺ–Ľ–ĺ–Ĺ–į –ł —Ä–Ķ–ī.
–Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä —Ā—É–ľ–į—ā–į –ĺ—ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į¬†–ľ–į—ā—Ä–ł—Ü–į, —Ā—ä—Ā—ā–ĺ—Ź—Č–į —Ā–Ķ –ĺ—ā –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ł—Ź –ļ–≤–į–ī—Ä–į—ā –ĺ—ā —Ä–Ķ–ī 2, –ļ–ĺ–Ľ–ĺ–Ĺ–į 2, –Ķ 22 =4. –ß–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į –ľ–į—ā—Ä–ł—Ü–į –≤ –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł 3 –ł 4 —Ā–Ķ —Ā—ä–Ī–ł—Ä–į—ā, –∑–į –ī–į –ī–į–ī–į—ā (3 + 4)2 = 49, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –ĺ—ā —Ā–Ī–ĺ—Ä–į –Ĺ–į 9+12+12+16, –į —Ā—É–ľ–į—ā–į –ĺ—ā —á–ł—Ā–Ľ–į—ā–į –≤ –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł 5, 6 –ł 7 –Ķ (5 + 6 + 7)2 = 324.

–Ę–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ —Ā¬†–Ĺ–ĺ–ľ–Ķ—Ä–į—ā–į –∑–į —Ä–Ķ–ī–ĺ–≤–Ķ—ā–Ķ, –Ĺ–į–Ņ–ł—Ā–į–Ĺ–ł –ĺ—ā –Ľ—Ź–≤–į—ā–į —Ā—ā—Ä–į–Ĺ–į, –ł –Ĺ–ĺ–ľ–Ķ—Ä–į—ā–į –∑–į –ļ–ĺ–Ľ–ĺ–Ĺ–ł—ā–Ķ, –Ĺ–į–Ņ–ł—Ā–į–Ĺ–ł –ĺ—ā–≥–ĺ—Ä–Ķ.
–Ę–ĺ–≤–į –ī–ĺ—Ä–ł –ł–∑–≥–Ľ–Ķ–∂–ī–į –≤–į–∂–ł, –ļ–ĺ–≥–į—ā–ĺ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į –Ķ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ł—Ä–į–Ĺ–į —á—Ä–Ķ–∑ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ –Ĺ–į –Ĺ–Ķ–Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł. –ź–ļ–ĺ –≤–∑–Ķ–ľ–Ķ–ľ –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ—ā–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł—ā–Ķ 1, 4 –ł 8, —Ā—É–ľ–į—ā–į –Ĺ–į (—Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–į—ā–į) –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į –Ķ (1+4+8)2 = 169.
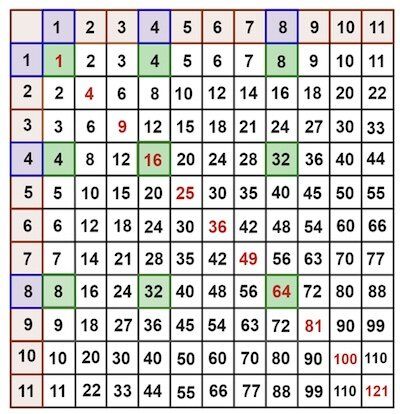
–ė–ľ–į –Ĺ—Ź–ļ–ĺ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–∑—Ä–Ķ–Ĺ–ł—Ź –∑–į—Č–ĺ —ā–ĺ–≤–į —Ä–į–Ī–ĺ—ā–ł —Ā —ā—Ä–ł —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į a, b –ł¬†c, –ł–∑–Ī—Ä–į–Ĺ–ł –ĺ—ā —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, –∑–į –ī–į –ī–Ķ—Ą–ł–Ĺ–ł—Ä–į—ā –ľ–į—ā—Ä–ł—Ü–į—ā–į, –ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į—ā –ĺ–Ī—Č–į —Ą–ĺ—Ä–ľ—É–Ľ–į, –ļ–ĺ—Ź—ā–ĺ —Ä–į–Ī–ĺ—ā–ł –∑–į –≤—Ā—Ź–ļ–į–ļ–≤–ł —ā—Ä–ł —á–ł—Ā–Ľ–į. –í –Ĺ–į—ą–ł—Ź –Ņ—Ä–ł–ľ–Ķ—Ä –Ņ–ĺ-–≥–ĺ—Ä–Ķ —Ā—É–ľ–į—ā–į –Ĺ–į —á–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į —Ä–Ķ—ą–Ķ—ā–ļ–į –Ķ:
|   | 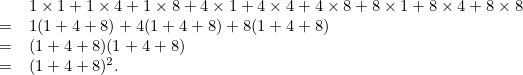 |
  |   |
–ė –Ņ–ĺ-–ĺ–Ī—Č–ĺ
|   |   |   |
–°—É–ľ–į—ā–į –ĺ—ā —á–ł—Ā–Ľ–į—ā–į –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–į—ā–į –ľ–į—ā—Ä–ł—Ü–į, —Ā—ä–∑–ī–į–ī–Ķ–Ĺ–į —á—Ä–Ķ–∑ –Ņ—Ä–Ķ—Ā–ł—á–į–Ĺ–Ķ –Ĺ–į –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł –Ĺ–į–Ī–ĺ—Ä –ĺ—ā —Ä–Ķ–ī–ĺ–≤–Ķ (a, b –ł¬†c) —Ā—ä—Ā —Ā—ä–≤–Ņ–į–ī–į—Č–ł—Ź –Ĺ–į–Ī–ĺ—Ä –ĺ—ā –ļ–ĺ–Ľ–ĺ–Ĺ–ł (a, b –ł¬†c), –Ĺ–ł –ī–į–≤–į –ļ–≤–į–ī—Ä–į—ā –Ĺ–į —Ā—É–ľ–į—ā–į –ĺ—ā¬†–Ĺ–ĺ–ľ–Ķ—Ä–į—ā–į –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ/–ļ–ĺ–Ľ–ĺ–Ĺ–ł (a+b+c)2
–ú–ĺ–∂–Ķ –Ľ–ł —ā–ĺ–≤–į –ī–į¬†–≤–į–∂–ł –∑–į —á–Ķ—ā–ł—Ä–ł —á–ł—Ā–Ľ–į, –Ņ–Ķ—ā —á–ł—Ā–Ľ–į –ł –Ņ–ĺ–≤–Ķ—á–Ķ?
–ö–≤–į–ī—Ä–į—ā–ł¬†–Ĺ–į –ļ–≤–į–ī—Ä–į—ā–ł –ł –ļ–≤–į–ī—Ä–į—ā–ł¬†–Ĺ–į –ļ—É–Ī–ĺ–≤–Ķ
–Ď–Ľ–į–≥–ĺ–ī–į—Ä–Ķ–Ĺ–ł–Ķ –Ĺ–į —ā–ĺ–≤–į –∑–Ĺ–į–Ĺ–ł–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į —Ä–į–∑–ļ—Ä–ł–Ķ–ľ –Ĺ—Ź–ļ–ĺ–ł –Ĺ–Ķ–ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä –ľ–ĺ–∂–Ķ—ā–Ķ –Ī—ä—Ä–∑–ĺ –ī–į –Ņ–ĺ–ļ–į–∂–Ķ—ā–Ķ (–ľ–ĺ–∂–Ķ –Ī–ł —Ā –ľ–į–Ľ–ļ–ĺ –Ľ–Ķ–≥–ĺ!), —á–Ķ —Ā—É–ľ–į—ā–į –ĺ—ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ĺ–Ķ—á–Ķ—ā–Ĺ–ł —á–ł—Ā–Ľ–į (–∑–į–Ņ–ĺ—á–≤–į—Č–ł –ĺ—ā 1) –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į –ļ–≤–į–ī—Ä–į—ā. –Ě–Ķ–ļ–į –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –Ņ—Ä–Ķ—Ā–ł—á–į—Č–ł—ā–Ķ —Ā–Ķ —Ä–Ķ–ī–ĺ–≤–Ķ, –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł —Ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ĺ–Ķ—á–Ķ—ā–Ĺ–ł —á–ł—Ā–Ľ–į —Ā—ä—Ā —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—Č–ł—ā–Ķ –ļ–ĺ–Ľ–ĺ–Ĺ–ł.

–°—É–ľ–į—ā–į –ĺ—ā –Ĺ–ĺ–ľ–Ķ—Ä–į—ā–į –Ĺ–į —Ä–Ķ–ī/–ļ–ĺ–Ľ–ĺ–Ĺ–į —Č–Ķ –Ī—ä–ī–Ķ –ļ–≤–į–ī—Ä–į—ā –Ĺ–į —á–ł—Ā–Ľ–ĺ, —ā—ä–Ļ –ļ–į—ā–ĺ —ā–ĺ–≤–į –Ķ —Ā—É–ľ–į—ā–į –ĺ—ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ĺ–Ķ—á–Ķ—ā–Ĺ–ł —á–ł—Ā–Ľ–į, –∑–į –ļ–ĺ—Ź—ā–ĺ –∑–Ĺ–į–Ķ–ľ, —á–Ķ –Ķ –ļ–≤–į–ī—Ä–į—ā. –ė –ļ–≤–į–ī—Ä–į—ā—ä—ā –Ĺ–į —Ā—É–ľ–į—ā–į –ĺ—ā –Ĺ–ĺ–ľ–Ķ—Ä–į—ā–į –Ĺ–į —Ä–Ķ–ī/–ļ–ĺ–Ľ–ĺ–Ĺ–į —Č–Ķ –Ī—ä–ī–Ķ –ļ–≤–į–ī—Ä–į—ā –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ: —ā–ĺ–≤–į –Ķ —á–ł—Ā–Ľ–ĺ, –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ĺ –Ĺ–į —á–Ķ—ā–≤—ä—Ä—ā–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ. –Ę–į–ļ–į —á–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –Ņ–ĺ–Ľ—É—á–ł–ľ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ–Ĺ–ł —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į, –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ł –Ĺ–į 4-—ā–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ –ĺ—ā —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ļ–ļ–ł —ā–į–∑–ł –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–į –ľ–į—ā—Ä–ł—Ü–į.
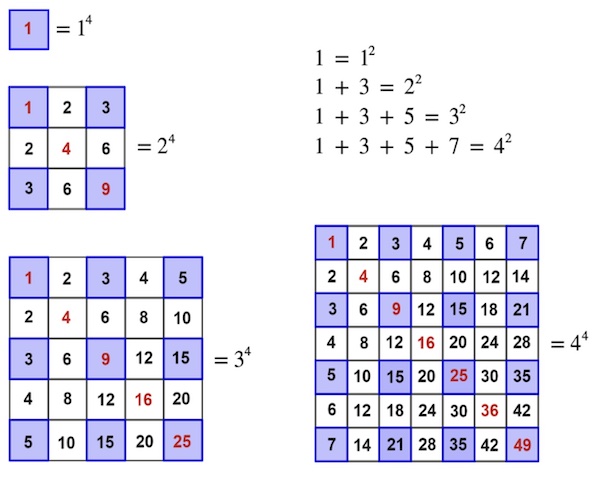
–°—É–ľ–ł—ā–Ķ –Ĺ–į —Ā–ł–Ĺ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā—á–Ķ—ā–į –≤ –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –Ĺ–Ķ—á–Ķ—ā–Ĺ–ł—ā–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–ł—Ä–į–Ĺ–ł —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł –Ĺ–ł –ī–į–≤–į—ā —á–ł—Ā–Ľ–į, –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ł –Ĺ–į 4-—ā–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ.
–ú–ĺ–∂–Ķ –ī–į –Ņ–ĺ–Ľ—É—á–ł–ľ –ī—Ä—É–≥ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ķ–Ĺ —Ä–Ķ–∑—É–Ľ—ā–į—ā, —á–Ķ –ļ—É–Ī–ł—á–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ (—á–ł—Ā–Ľ–ĺ, –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ĺ –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ 3) –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –∑–į–Ņ–ł—Ā–į–Ĺ–ĺ –ļ–į—ā–ĺ —Ā–Ī–ĺ—Ä –ĺ—ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ĺ–Ķ—á–Ķ—ā–Ĺ–ł —á–ł—Ā–Ľ–į. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä 13 = 1, 23 = 8 = 3 + 5 –ł 33 = 27 = 7 + 9 + 11.
–Ę–į–ļ–į —á–Ķ, –į–ļ–ĺ –ł–∑–Ī–Ķ—Ä–Ķ–ľ –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł –ľ–į—ā—Ä–ł—Ü–ł, –ļ–ĺ–ł—ā–ĺ —Ā–į –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į —ā–Ķ–∑–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ĺ–Ķ—á–Ķ—ā–Ĺ–ĺ –Ĺ–ĺ–ľ–Ķ—Ä–ł—Ä–į–Ĺ–ł —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł, —Ā—É–ľ–į—ā–į –ĺ—ā —á–ł—Ā–Ľ–į—ā–į –≤ —ā–Ķ–∑–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł –ľ–į—ā—Ä–ł—Ü–ł —Č–Ķ –Ī—ä–ī–Ķ –ļ–≤–į–ī—Ä–į—ā –Ĺ–į –ļ—É–Ī–ł—á–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ķ —á–ł—Ā–Ľ–ĺ, –Ņ–ĺ–≤–ī–ł–≥–Ĺ–į—ā–ĺ –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ 6. –ó–Ķ–Ľ–Ķ–Ĺ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł –Ņ–ĺ-–ī–ĺ–Ľ—É —Ā–į –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł 3 –ł 5, –į —Ā–Ī–ĺ—Ä—ä—ā –ł–ľ –Ķ (3+5)2 = (23)2 = 26.
–ź –∂—ä–Ľ—ā–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł —Ā–į –Ņ—Ä–Ķ—Ā–Ķ—á–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į —Ä–Ķ–ī–ĺ–≤–Ķ –ł –ļ–ĺ–Ľ–ĺ–Ĺ–ł 7, 9 –ł 11, —ā–į–ļ–į —á–Ķ —ā—Ź—Ö–Ĺ–į—ā–į —Ā—É–ľ–į –Ķ (7+9+11)2 = (33)2 = 36.

–£—á–ł—ā–Ķ–Ľ–ł—ā–Ķ –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –≤–ł–Ĺ–į–≥–ł —ā—ä—Ä—Ā—Ź—ā –Ĺ–ĺ–≤–ł –Ĺ–į—á–ł–Ĺ–ł –ī–į –≤—ä–≤–Ķ–ī–į—ā —É–Ķ–Ĺ–ł—Ü–ł—ā–Ķ¬†–≤ –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł–ł—ā–Ķ –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ł –į–Ľ–≥–Ķ–Ī—Ä–į. –ź–ļ–ĺ –∑–į–Ņ–ĺ—á–Ĺ–Ķ–ľ –ī–į –ľ–ł—Ā–Ľ–ł–ľ –Ĺ–Ķ–ļ–ĺ–Ĺ–≤–Ķ–Ĺ—Ü–ł–ĺ–Ĺ–į–Ľ–Ĺ–ĺ, –ĺ—ā–ļ—Ä–ł–≤–į–ľ–Ķ, —á–Ķ —ā–į–Ī–Ľ–ł—Ü–į—ā–į –∑–į —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ķ –Ĺ–Ķ—Č–ĺ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā –Ņ—Ä–ĺ—Ā—ā–ĺ —Ā—ā—Ä–Ķ–ī—Ā—ā–≤–ĺ –∑–į –∑–į–Ņ–ĺ–ľ–Ĺ—Ź–Ĺ–Ķ. –ź–ļ–ĺ —Ä–Ķ—ą–ł–ľ –ī–į —Ā–Ķ –Ņ–ĺ—ā–ĺ–Ņ–ł–ľ –ī—ä–Ľ–Ī–ĺ–ļ–ĺ –≤ –ļ—Ä–ł—Ā—ā–į–Ľ–Ĺ–ĺ —Ā–ł–Ĺ–ł—ā–Ķ –≤–ĺ–ī–ł, —Č–Ķ –ĺ—ā–ļ—Ä–ł–Ķ–ľ –ľ–Ĺ–ĺ–≥–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —Ā—ä–ļ—Ä–ĺ–≤–ł—Č–į –≤ –Ĺ–Ķ–Ļ–Ĺ–ĺ—ā–ĺ –ľ–ĺ—Ä—Ā–ļ–ĺ –ī—ä–Ĺ–ĺ.
–°—ā–į—ā–ł—Ź—ā–į –Ķ –Ņ—Ä–Ķ–≤–ĺ–ī –Ĺ–į –Ņ—É–Ī–Ľ–ł–ļ–į—Ü–ł—Ź—ā–į –≤ —Ā–Ņ–ł—Ā–į–Ĺ–ł–Ķ¬†Plus –Ĺ–į¬†–£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –ö–Ķ–Ļ–ľ–Ī—Ä–ł–ī–∂.
–ź–≤—ā–ĺ—Ä–ł—ā–Ķ —Ā–į –ī–≤–į–ľ–į —É—á–ł—ā–Ķ–Ľ–ł –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į:
 |
–Ę–ĺ–Ĺ–ł –§–ĺ—Ā—ā—ä—Ä (Tony Foster) –Ņ–ĺ–ľ–į–≥–į –Ĺ–į —Ö–ĺ—Ä–į —Ā –Ņ—Ā–ł—Ö–ł—á–Ĺ–ł –∑–į–Ī–ĺ–Ľ—Ź–≤–į–Ĺ–ł—Ź –ī–į –Ĺ–į–ľ–Ķ—Ä—Ź—ā —Ü–Ķ–Ľ –≤ –∂–ł–≤–ĺ—ā–į. –ě—Ā–≤–Ķ–Ĺ —ā–ĺ–≤–į –Ķ –į–ľ–į—ā—Ć–ĺ—Ä –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ł –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–ł—ā–Ķ –ľ—É –≤–ļ–Ľ—é—á–≤–į—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł–ļ–į –Ĺ–į –ü–į—Ā–ļ–į–Ľ, –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł —Ä–Ķ–ī–ł—Ü–ł –ł –ļ–ĺ–ľ–Ī–ł–Ĺ–į—ā–ĺ—Ä–ł–ļ–į. –Ě–Ķ–≥–ĺ–≤–ł—ā–Ķ –ĺ—ā–ļ—Ä–ł—ā–ł—Ź —Ā–į –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–ł –≤ Mathematics Teacher journal, Mathematical Gazette –ł Interactive Mathematics Miscellany and Puzzles. |
 |
–°–į–Ļ –í–Ķ–Ĺ–ļ–į—ā–Ķ—ą (Sai Venkatesh) –Ķ –Ķ–Ĺ—ā—É—Ā–ł–į—Ā—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ł —Ā—ā—Ä–į—Ā—ā–Ķ–Ĺ —É—á–ł—ā–Ķ–Ľ. –Ę–ĺ–Ļ –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į –Ĺ–į —É—á–Ķ–Ĺ–ł—Ü–ł –ĺ—ā –Ņ—Ä–ĺ–≥–ł–ľ–Ĺ–į–∑–ł–į–Ľ–Ķ–Ĺ –ł –≥–ł–ľ–Ĺ–į–∑–ł–į–Ľ–Ķ–Ĺ –ļ–Ľ–į—Ā –≤ Step By Step School, –Ě–ĺ–Ļ–ī–į, –ė–Ĺ–ī–ł—Ź. –Ę–ĺ–Ļ –≤—Ź—Ä–≤–į, —á–Ķ —É—á–Ķ–Ĺ–ł—Ü–ł—ā–Ķ —Ā–Ķ –Ĺ–į—Ā–Ľ–į–∂–ī–į–≤–į—ā –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į —ā–ĺ—á–Ĺ–ĺ –ļ–į–ļ—ā–ĺ —Ā–Ķ –Ĺ–į—Ā–Ľ–į–∂–ī–į–≤–į—ā –Ĺ–į –≤—Ā—Ź–ļ–į –ī—Ä—É–≥–į —Ą–ĺ—Ä–ľ–į –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ. |


















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.
dolivo
–ó–Ķ–ľ–Ĺ–į—ā–į —Ź–Ī—ä–Ľ–ļ–į: —Ā—ā–į—Ä–į –ļ—É–Ľ—ā—É—Ä–į –∑–į –Ĺ–ĺ–≤–ł—ā–Ķ –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ĺ–į