
Фракталните структури са най-видими при растенията. По същество, самият им растеж е подчинен на итерации.

Примерите за фрактали в растителния свят са многобройни, някои очевидни, други не толкова. Самата цикличност на растежа им обуславя самоподобието и оттам фракталната структура. Друг фактор е стремежът на по същество линейни сегменти като клоните да запълват площ или обем заради цели като повече светлина, въздух, вода, хранителни вещества (при корените), жизнено пространство. Тази тенденция на запълване на по-висши измерения е подобна на дробната размерност на фракталите и оформя подобни структури.
 |
 |
 |
||
| play | pause | |
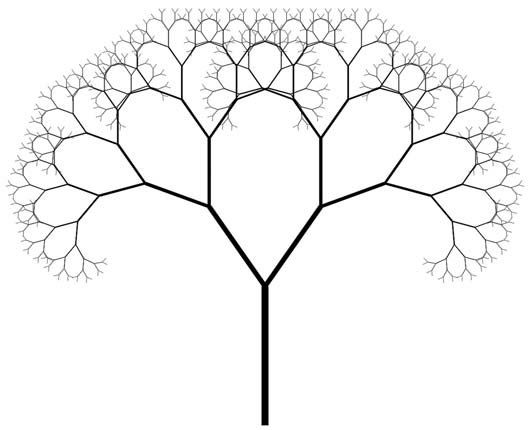
Повечето растения имат някаква форма на разклонение - основното стъбло се разделя на няколко клона, всеки от тях се разделя на по-малки клонки и това продължава до най-малките клончета.
Вероятно сте обърнали внимание, че клонче от дървото изглежда подобно на цялото дърво и листче от папрат изглежда почти идентично на целото растение.
Това всъщност се нарича самоподобие - едно от най-важните свойства на фракталите.
Папрат на Барнсли
Едни от най-популярните фрактали са папратите, получени от британския математик Майкъл Барнсли (Michael Barnsley) през 1988г. и подробно разгледахме как се генерират в темата Системи Итеративни Функции (Iterated Functions System - IFS). Могат да се разглеждат като вариант на дървовидните фрактали.

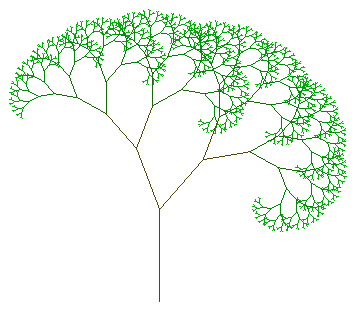
L-системите
Лесен начин за създаване на фрактални растения са L-системите на Линденмайер, разгледани в темата за итерациите. Тези фрактални модели стават класически примери, а за да се постигне още по-голям реализъм, се добавя параметър, генериращ случайни числа - колкото е по-голям диапазона им, толкова формите ще изглеждат по-естествени.
 |
 |
 |
 |
 |
 |
Още няколко примера на подобни на растения фрактали.

Фракталната коренова система

 |
| Оставете мишката върху изображението, за да се задвижи процеса DLA. |
Много фактори влияят върху растежа на корените на растенията. От особен интерес е съпротивлението в резултат на физическата бариера на почвата. За да проникнат в по- плътна почва, корени се сгъстяват и им темпът им на растеж се понижава.
Механизмът на растеж на кореновата система се оформя под влиянието на съпротивлението на почвата във фрактален процес, наречен DLA (Diffusion-Limited Aggregation) - "дифузия, ограничена от агрегация". В случая ниската концентрация на блуждаещи частици в среда, се замества с плътността и съпротивлението на средата.

Романеско
Името на този зеленчук показва, че идва от някъде около Рим - Romanesco означава "римски" на италиански и е известен сравнително от скоро - на международните пазари се е появил едва през 90-те години на ХХ век.
Този роднина на броколите и карфиола е като еталон за растителен фрактал. Някои градинари се шегуват, че това е извънземен зеленчук и че им приличал на летяща чиния. Аз не знам на какво приличат летящите чинии, но яркозелените му глави са триумф на самоподобието. Ако се вгледате в този вид броколи, увеличавайки мащаба, ще откривате все по-малки и по-малки, вложени едно в друго копия.
И за да се дооформи математическия вид на романеско, разклоняващите се пъпки (меристеми) са подредени в логаритмична спирала, а броят на спиралите са винаги някое от числата на Фибоначи.
Леонардо да Винчи
 Първото описание на фрактален модел в природата е на големия Леонардо да Винчи. Леонардо пише в тетрадките си: "Всички клони на едно дърво, на всеки етап от неговата височина, когато се съберат са равни на дебелината на ствола [под тях]." Това извод е известен като правило на Леонардо за клоните. Великият учен и художник предположил, че клонове действат като тръби, по които се движат течности, а общата площ на напречното сечение трябва да е една и съща при различни нива на дървото. Това правило не съвпада с реалното положение на нещата, но все пак Леонардо отново прави гениална догадка.
Първото описание на фрактален модел в природата е на големия Леонардо да Винчи. Леонардо пише в тетрадките си: "Всички клони на едно дърво, на всеки етап от неговата височина, когато се съберат са равни на дебелината на ствола [под тях]." Това извод е известен като правило на Леонардо за клоните. Великият учен и художник предположил, че клонове действат като тръби, по които се движат течности, а общата площ на напречното сечение трябва да е една и съща при различни нива на дървото. Това правило не съвпада с реалното положение на нещата, но все пак Леонардо отново прави гениална догадка.
Те не са перфектни
Все пак, отличителна черта на растителните фрактални модели е полусходството. Те не са "перфектни" фрактални структури, защото са определени в краен брой стъпки и да се състоят от краен брой сегменти, докато понятието фрактал се определя само като безкраен стремеж към определен предел.
Основни понятия и лексика
- Фрактал
- Самоподобие
- Итерация
- Дървовидни структури
- Папрат на Барнсли
- L-системите
- Романеско
- Полусходство
- Майкъл Барнсли
- Леонардо да Винчи
Източници:
Fractal properties of plants (pdf)
Романеско броколи – извънземен зеленчук


























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
10.02 2015 в 16:29
04.02 2015 в 10:59
27.01 2015 в 14:37
Благодаря на автора на статиите!!!
27.01 2015 в 14:33
http://en.wikipedia.org/wiki/Benoit_Mandelbrot
26.01 2015 в 10:43
Последни коментари
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години
Peter Petrov
След многократни експлозии нов тест за мегаракетата на Мъск
поп Дръвчо
Гледайте за първи път на живо как новооткритият "междузвезден посетител" 3I/ATLAS се устремява към нас
Bai Tanas
Как е миришел Древният Рим? Честно казано - ужасно!